lecture04

1.

Элементы теории перколяции

2.

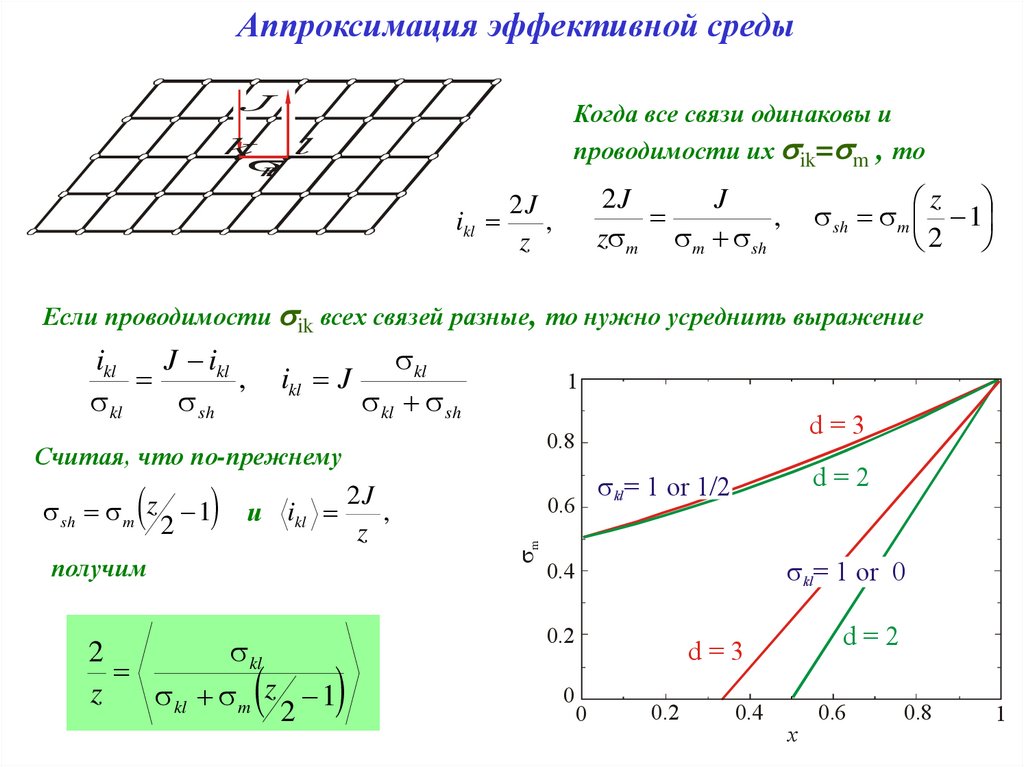
Аппроксимация эффективной среды
J
Когда все связи одинаковы и
проводимости их ik= m , то
k
l
k
l
z
sh m 1
2
2J
J
,
z m m sh
2J
ikl
,
z
Если проводимости ik всех связей разные, то нужно усреднить выражение
ikl
J ikl
,
kl
sh
ikl J
kl
kl sh
1
Считая, что по-прежнему
получим
2
kl
z
kl m z 1
2
d=2
kl= 1 or 1/2
0.6
m
sh m z 1
2
2J
,
и ikl
z
d=3
0.8
kl= 1 or 0
0.4
0.2
0
d=2
d=3
0
0.2
0.4
x
0.6
0.8
1

3.

Проблемы аналитических решений перколяционных задач
Ниже порога x < xc
n1 x (1 x ) 4
x sns
n2 2 x 2 (1 x )6
n3 2 x (1 x ) 4 x (1 x )
3
n=4
8
3
7
s
n=5
n=6

4.

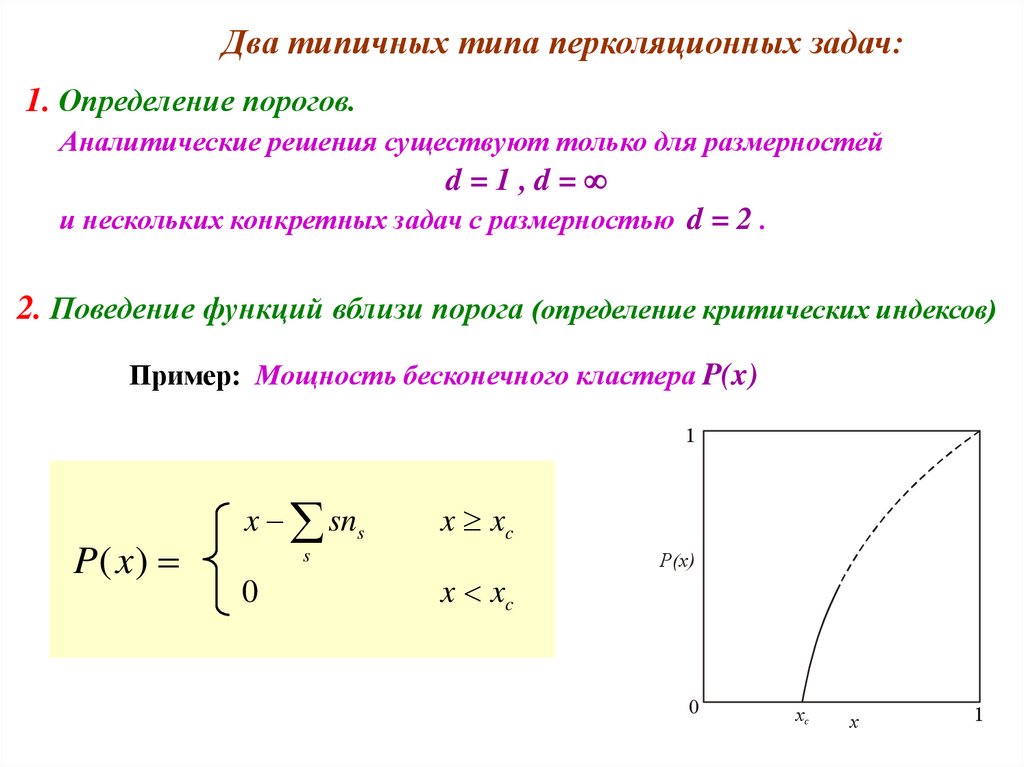
Два типичных типа перколяционных задач:
1. Определение порогов.
Аналитические решения существуют только для размерностей
d=1,d=
и нескольких конкретных задач с размерностью d = 2 .
2. Поведение функций вблизи порога (определение критических индексов)
Пример: Мощность бесконечного кластера P(x)
1
P(x )
x sns
x xc
s
0
x xc
P(x)
0
xc
x
1

5.

x=
0.58
< xc
x=
0.60
xc
Перколяция в задаче узлов
x=
0.62
> xc
на квадратной решетке
160 160
Из книги
J. Feder, Fractals (Plenum Press, 1988)
Есть русский перевод
Дж. Федер, Фракталы, 1991)

6.

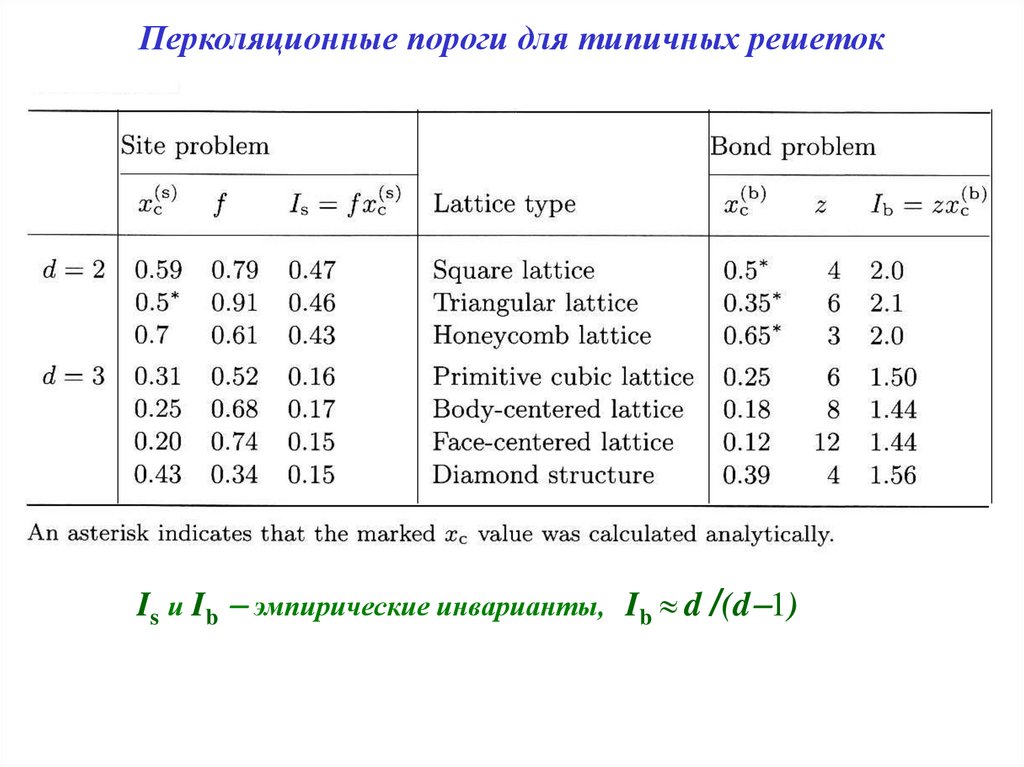
Перколяционные пороги для типичных решеток
Is и Ib эмпирические инварианты, Ib d /(d 1)

7.

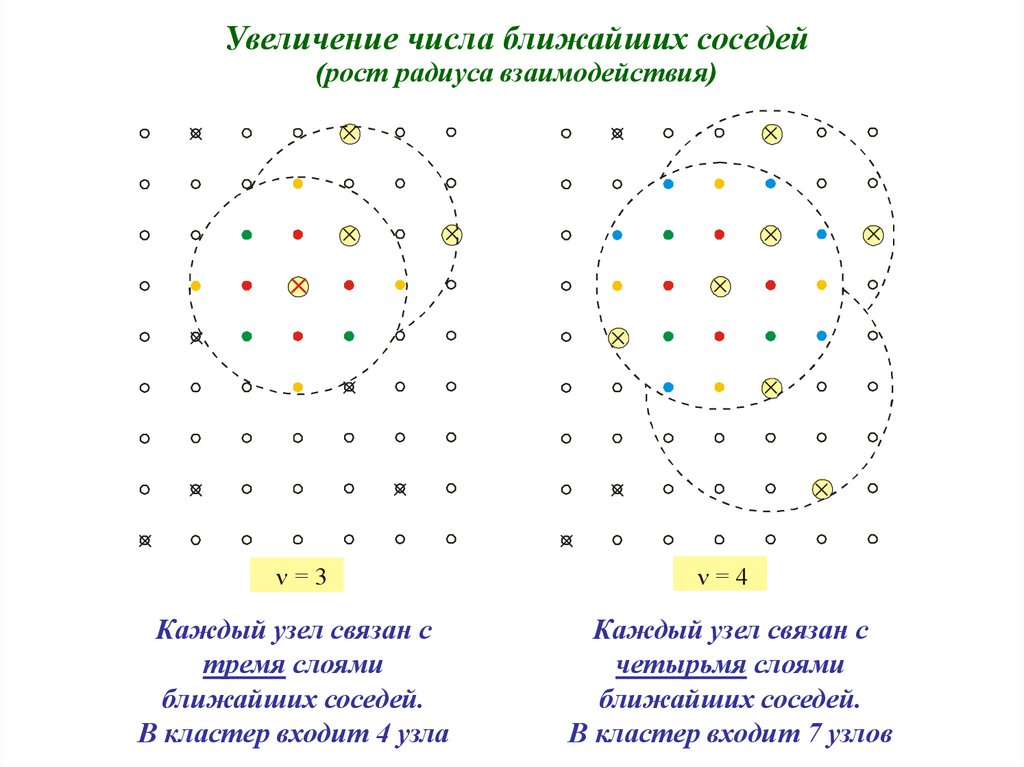
Увеличение числа ближайших соседей
(рост радиуса взаимодействия)
= 3
Каждый узел связан с
тремя слоями
ближайших соседей.
В кластер входит 4 узла
= 4
Каждый узел связан с
четырьмя слоями
ближайших соседей.
В кластер входит 7 узлов

8.

Перколяция в системе случайных узлов
3D
П
р
о
с
т
а
я
к
у
б
и
ч
е
с
к
а
я
О
б
ъ
е
м
н
о
Г
р
а
н
е
ц
е
н
т
р
и
р
о
в
а
н
н
а
яц
е
н
т
р
и
р
о
в
а
н
н
а
я
Ч
и
с
л
о
1 2 3 1 2 3 1 2 3
с
л
о
е
в
Ч
и
с
л
о
z
8 2
6 8 1
42
6 1
8 4
2
21
с
о
с
е
д
е
й 6 1
К
о
н
ц
е
н
т
р
.0
.3
10
.1
40
.0
90
.1
90
.1
40
.0
6
.1
00
.2
50
.1
80
x
c
zx
c
1
.8
42
.4
52
.4
71
.8
42
.4
52
.5
2
.5
21
.9
42
.4
52
Когда радиус взаимодействия r много больше периода решетки,
существенно лишь количество узлов внутри этого радиуса, т.е.
4 3
r N (N - концентрация),
3
а их взаимное расположение (симметрия решетки) несущественно.
4 3
r N c Bc( 3) 2.7,
3
r 2 N c Bc( 2 ) 4.4

9.

Континуальные задачи
U min U (r) U max ,
U (r) 0
S1 + S2 =1
Для размерности d = 2
на пороге
S1
S2
S1 = S2 =1/2
Функция U(r) предполагается статистически симметричной
относительно преобразования U
U
и статистически изотропной

10.

Окрестность перколяционного перехода
Статфункции концентрации открытых узлов
Вспомогательные функции
q(r,x) вероятность того, что узел на расстоянии r от открытого
узла тоже открыт и принадлежит тому же конечному кластеру
q(0)=1, q(a)=x
w(s,x) вероятность того, что открытый узел
принадлежит к конечному кластеру с s узлами
Основные функции
Мощность бесконечного кластера P(x);
Среднее число узлов конечного кластера S(x);
S ( x ) q( r ) sw( s )
r
2
s
s ns
s
sn
s
P(xс)= 0
S(xс)=
s
x(xс) =
Корреляционная длина x (x);
x2 ( x )
sns
w( s )
s sns
2
r
r q(r )
q( r )
r
2
r
r q(r )
S ( x)

11.

Основной постулат :
В окрестности перколяционного перехода P, S и x степенные
функции разности | x xc |
P ( x ) ( x xc ) ,
S ( x ) | x xc |
x ( x ) | x xc |
x > xc
Критические индексы и
одинаковы по обе стороны порога
Значения критических индексов
P
x
S
d=2
5
/36
4
/3
43
/18
d=3
0
.4
1
7
0
.8
7
5
1
.7
9
5
Аналогия с фазовыми переходами
второго рода
Концентрация х
Температура Т
Мощность
бесконечного
кластера Р
Параметр
порядка
x
Получены
аналитически
Получены
численно
Корреляционная
длина
x

12.

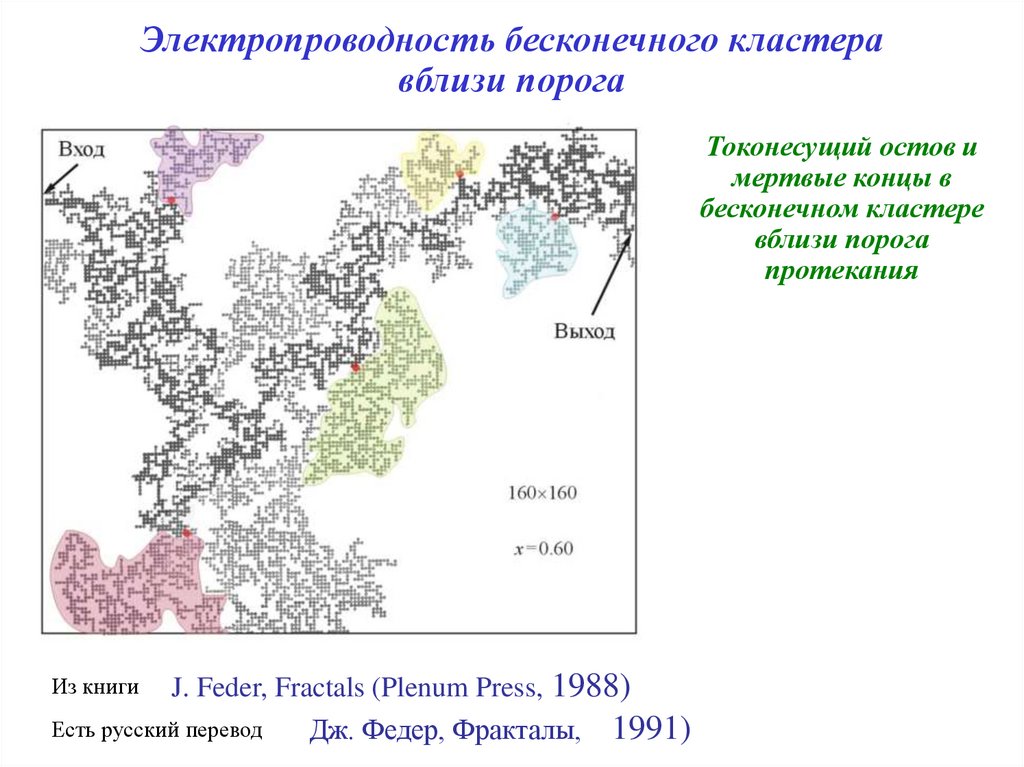
Электропроводность бесконечного кластера
вблизи порога
Токонесущий остов и
мертвые концы в
бесконечном кластере
вблизи порога
протекания
J. Feder, Fractals (Plenum Press, 1988)
Есть русский перевод
Дж. Федер, Фракталы, 1991)
Из книги

13.

Задача: Найти сопротивление простой кубической решетки,
связи в которой имеют сопротивления в экспоненциально
большом интервале значений
R R0eu ,
0 u u0 ,
u0 >> 1,
u случайная величина, с вероятностью F(u)=const=1/u0
принимающая любые значения из разрешенного интервала.
Постепенно включаем связи, начиная с самых высокопроводящих (u=0) до
тех пор, пока при некотором uc
uc
uc
x F (u)du xc ,
u0
0
uc xcu0 ( 0.25u0 ).
Чтобы по бесконечному кластеру пошел ток, порог xc должен быть
превышен на Dx = x xc= Du/u0 . Корреляционная длина при этом конечна
u
x a 0
Du

14.

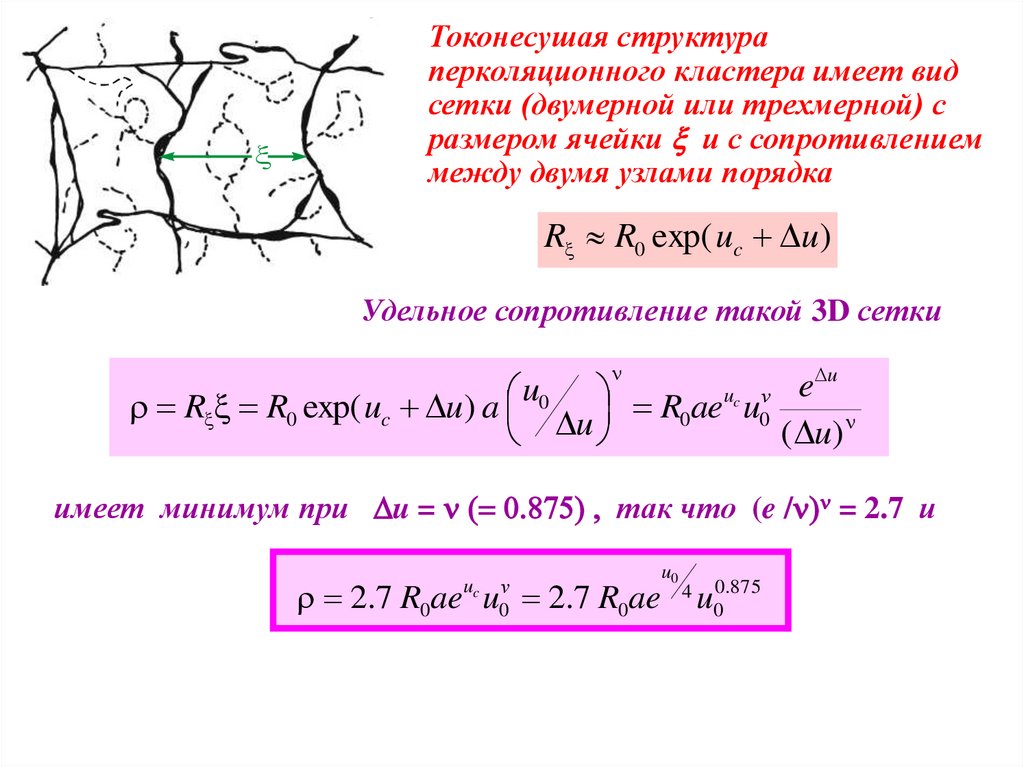
x
Токонесушая структура
перколяционного кластера имеет вид
сетки (двумерной или трехмерной) с
размером ячейки x и с сопротивлением
между двумя узлами порядка
Rx R0 exp( uc Du )
Удельное сопротивление такой 3D сетки
Du
u0
uc ν e
Rxx R0 exp( uc Du) a
R0ae u0
D
u
( Du)
имеет минимум при Du = 0.875 , так что (e / = 2.7 и
u0
2.7 R0ae u 2.7 R0ae 4 u00.875
uc
ν
0