12 Описательная статистика - подготовка к КР

1.

вероятность
и статистика
7 класс

2.

ОТВЕТЬТЕ
НА
ВОПРОСЫ
01
дайте определение среднего значения
числового набора и расскажите, как его
вычислить.
02
дайте определение медианы числового
набора и расскажите, как ее вычислить.
03
дайте определение размаха числового
набора
и
расскажите,
как
его
вычислить.
04
в
каких
случаях
среднее
арифметическое не очень хорошо
описывает большинство значений в
числовом наборе?
05
в чем главное достоинство медианы как
центральной меры?

3.

проверка
домашнего
задания

4.

стр 42 № 65
а) наибольшее значение = 25
б) наибольшее значение = 47
наименьшее значение = 3
наименьшее значение = 5
размах = 25 - 3 = 22
размах = 47 - 5 = 42
среднее арифметическое
12 + 7 + 25 + 3 + 19 + 15
среднее арифметическое
17 + 19 + 5 + 41 + 47 + 13 + 19
6
= 13, 5
медиана 3, 7, 12, 15, 19, 25
(12 + 15) : 2 = 13, 5
7
медиана 5, 13, 17, 19, 19, 41, 47
= 23

5.

стр 42 № 66
а) самый большой по числу жителей в
2021 г. город России Москва
б) второй по населению город России
в 2021 г. Санкт-Петербург
в) третий и четвёртый по числу
жителей города России в 2021 г. Новосибирск
Екаберинбург
стр 42 № 67
а) наибольшее значение 135,5
наименьшее значение 70,9
размах 135,5 - 70,9 = 64,6
б) наибольшее значение 29,2
наименьшее значение 18,3
размах 29,2 - 18,3 = 10,9

6.

работаем
в тетради

7.

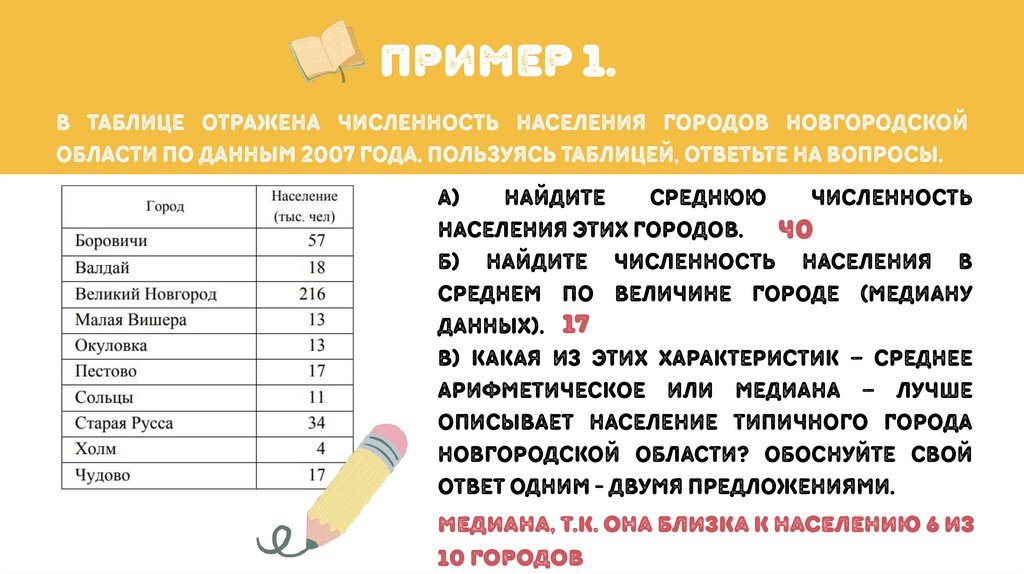
пример 1.
В таблице отражена численность населения городов Новгородской
области по данным 2007 года. пользуясь таблицей, ответьте на вопросы.
а)
Найдите
среднюю
численность
населения этих городов. 40
б) Найдите численность населения в
среднем по величине городе (медиану
данных). 17
в) Какая из этих характеристик – среднее
арифметическое или медиана – лучше
The Spectacular Speaker
описывает население
типичного
Award is given
to students who города
have demonstrated
inspiring
Новгородской области?
Обоснуйте
свой
confidence in their
ответ одним - двумя
предложениями.
communication skills.
медиана, т.к. она близка к населению 6 из
10 городов

8.

пример 2.
В таблице приведена приближенная численность учащихся и учителей
общеобразовательных школ и интернатов в России по годам (тыс.чел. к
началу учебного года).
а) В начале какого учебного года (из данных в таблице) число
школьников в России было наибольшим? 1970/71
б) На сколько процентов уменьшилось число учащихся к сентябрю 2006
года по сравнению с сентябрем 1950 года? примерно на 23%
в) Сравните данные в начале 1940/41 учебного года и в начале 1990/91
учебного года. Как изменилась за пятьдесят лет численность учащихся?
Численность учителей? численность учащихся не изменилась, численность учителей
увеличилась примерно в 2 раза

9.

пример 3.
Дан числовой набор из 9 чисел. Среднее арифметическое набора 5. Из
набора удалили одно число, и среднее арифметическое стало равно 6.
а) Какое число удалили?
б) Если все числа нового набора сначала увеличить на 2, а потом
умножить на 3, чему станет равно среднее арифметическое полученного
набора?
решение:
а) Начальный набор чисел:
ср. ариф. = 5
количество = 9
сумма чисел = 9 ⋅ 5 = 45
новый набор чисел
ср. ариф. = 6
количество = 8
сумма чисел = 8 ⋅ 6 = 48
45 - 48 = -3 - это число удалили

10.

пример 3.
Дан числовой набор из 9 чисел. Среднее арифметическое набора 5. Из
набора удалили одно число, и среднее арифметическое стало равно 6.
а) Какое число удалили?
б) Если все числа нового набора сначала увеличить на 2, а потом
умножить на 3, чему станет равно среднее арифметическое полученного
набора?
решение:
б) (х 1+ 2 + х 2+ 2 + х 3 + 2 + х 4+ 2 + х 5+ 2 + х6 + 2 + х7 + 2 + х 8+ 2) ⋅ 3
8
(48 + 2 ⋅ 8) ⋅ 3
= 24
=
8
(сумма чисел + 2 ⋅ 8) ⋅ 3
=
8

11.

пример 4.
На соревнованиях по фигурному катанию каждый элемент имеет базовую
стоимость и судейскую оценку. Девять судей независимо друг от друга
выставляют за каждый элемент свои оценки от –5 до +5 баллов. Затем
самая высокая и самая низкая оценки отбрасываются. Среднее
арифметическое оставшихся семи оценок, округлённое до сотых,
прибавляется к базовой стоимости. Полученная сумма является
итоговой оценкой за элемент. Фигуристу Артёму Петрову судьи поставили
оценки за три элемента. Эти оценки и базовая стоимость каждого
элемента показаны в таблице. Определите, за какой элемент Артём Петров
получил наиболее высокую оценку. В ответе запишите этот элемент и
оценку за него.

12.

пример 4.
решение:
Сальхов
Каскад
0+1+1+1+1+1+1
7
0,86 + 4,3 = 5, 16
-2 + (-2) + (-2) + (-1) + (-2 ) + (-3) + (-1)
7
Лутц
-1 + 0 + 0 + (-1) + 0 + 0 + 0
7
-0,29
-1,86
6,1 + (-1,86) = 4,24
5,9 + (-0,29) = 5,61
Ответ: Лутц: 5,61.

13.

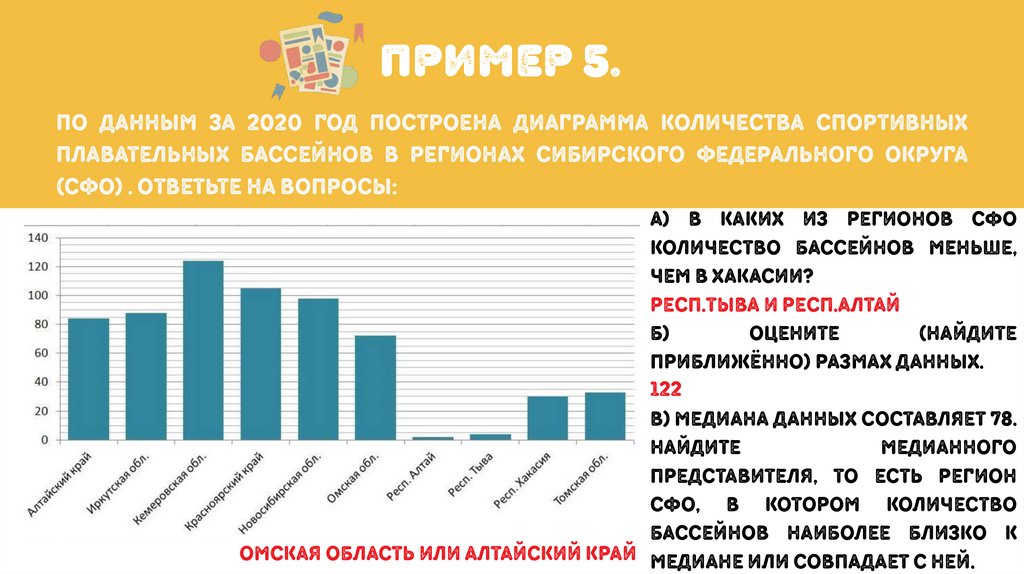
пример 5.
По данным за 2020 год построена диаграмма количества спортивных
плавательных бассейнов в регионах Сибирского федерального округа
(СФО) . Ответьте на вопросы:
а) В каких из регионов СФО
количество бассейнов меньше,
чем в Хакасии?
Респ.тыва и респ.алтай
б)
Оцените
(найдите
приближённо) размах данных.
122
в) Медиана данных составляет 78.
Найдите
медианного
представителя, то есть регион
СФО, в котором количество
бассейнов наиболее близко к
Омская область или алтайский край медиане или совпадает с ней.

14.

домашнее задание
подготовиться к
контрольной
работе по главе 2