Similar presentations:
Вероятность и статистика. 7 класс
1.
Вероятность и статистика7 класс
2.
Средняя цена = 8 150 руб.Среднее арифметическое
хорошо описывает
массивы однородных
данных.
Магазин
Цена
Магазин
Цена
1
8 050
6
7 790
2
8 480
7
8 290
3
8 590
8
7 890
4
8 340
9
7 970
5
8 190
10
7 910
3.
МагазинЦена, руб
Магазин
Цена, руб
1
8 050
6
7 790
2
8 480
7
8 290
3
8 590
8
7 890
4
8 340
9
7 970
5
8 190
10
14 590
Средняя цена = 9 948 руб.
выброс
В таких случаях в качестве центральной меры часто используют медиану.
4.
Медиана числового набора.Устойчивость медианы.
5.
6.
7.
8.
9.
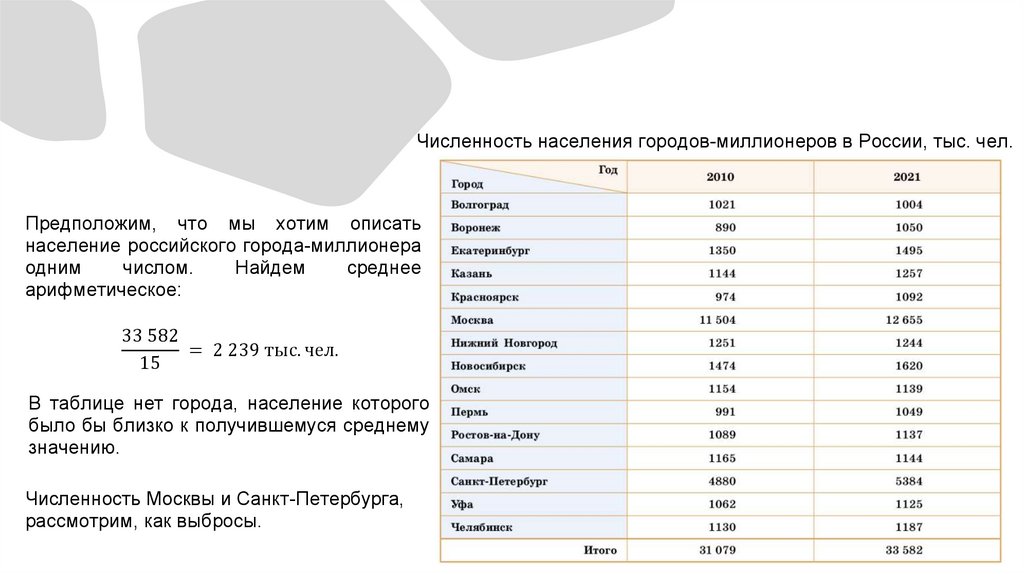
Численность населения городов-миллионеров в России, тыс. чел.Предположим, что мы хотим описать
население российского города-миллионера
одним
числом.
Найдем
среднее
арифметическое:
33 582
= 2 239 тыс. чел.
15
В таблице нет города, население которого
было бы близко к получившемуся среднему
значению.
Численность Москвы и Санкт-Петербурга,
рассмотрим, как выбросы.
10.
Упорядочим значения:Численность населения городов-миллионеров в России, тыс. чел.
Медианой является восьмое по порядку
значение (выделено): 1144 тыс.чел.
Это население г. Самары.
Можно сказать, что Самара - медианный по
численности город-миллионер в 2021 году
или медианный представитель данного
набора.
Главное достоинство медианы устойчивость относительно выбросов.
11.
Устойчивость медианы.Пример: Предположим, что в числовом наборе 10 чисел. Есть правило, что
если увеличивать или уменьшать одно число набора (двигать его), то
среднее арифметическое будет двигаться в ту же сторону, но в 10 раз
медленнее. А как поведет себя медиана? Проще всего разобраться в этом на
примере. Рассмотрим набор из первых 10 натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Среднее арифметическое и медиана совпадают. Они равны 5,5.
а) Увеличим последнее число на 10, а потом еще на 100. Как изменятся
среднее и медиана?
б) Увеличим первое число на 10, а потом еще на 100. Как изменится
среднее и медиана в этом случае?
12.
Решение.а) Если увеличить последнее число 10 на 10, то среднее арифметическое
увеличится на 1 и станет равным 6,5.
А медиана останется прежней (5,5): она зависит только от двух серединных
чисел 5 и 6, которые не изменялись.
Если увеличить последнее число еще на 100, то среднее арифметическое
вырастет еще на 10 и теперь будет 16,5.
Медиана и в этом случае не изменится.
б) Увеличим теперь первое число 1 на 10. Получится 11. Среднее вырастет на
1 и станет равно 6,5.
Так как вариационный ряд теперь изменился, медиана изменилась тоже.
Серединными числами нового набора
2, 3, 4, 5, 6, 7, 8, 9, 10, 11
являются не числа 5 и 6, как прежде, а числа 6 и 7. Следовательно, медиана
теперь тоже равна 6,5. Но дальнейшее увеличение первого числа уже не
изменит медиану.
Если теперь первое число увеличить еще на 100, получится набор
2, 3, 4, 5, 6, 7, 8, 9, 10, 111,
где среднее стало равно 6,5 +10 =16,5, а медиана уже больше не изменилась.
13.
Домашняя работа§ 8 на стр. 36 изучить.
Выполнить № 54, 57 на стр. 39.
14.
Урок 2. Нахождение медианы,используя табличный процессор
15.
16.
Компьютерный практикум:1. Отройте файл в папке Рабочая
2. Скопируйте его в свою папку
3. Выполните задания используя встроенную функцию
СРЗНАЧ и МЕДИАНА
Год
Урожайность
зерновых, ц/га
2009
22,7
2010
18,3
2011
22,4
2012
18,3
2013
22,0
2014
24,1
2015
23,7
2016
26,2
2017
29,2
2018
27,2
17.
1. Найдите медиану числа жителей городов в 2010 году.2. Найдите медиану числа жителей городов в 2019 году.
3. Сравните медианы 2010 и 2019 годов
4. Найдите медианных представителей в эти года
18.
Домашняя работа§ 8 на стр. 36 повторить.
Выполнить № 60 в тетради, №
62 с использованием
табличного процессора.

















 mathematics
mathematics








