Similar presentations:
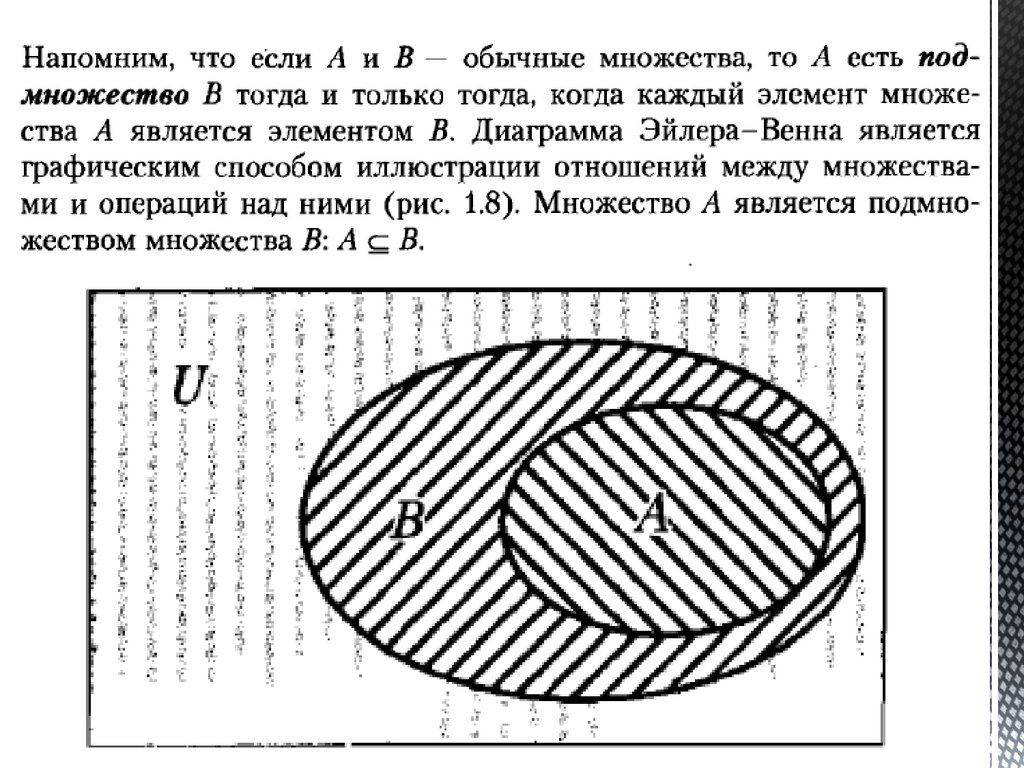
Математические основы интеллектуальных технологий. Операции над нечеткими множествами
1.
Математические основыинтеллектуальных технологий
Преподаватель –
Тонких Артём Петрович
2.
Операции над нечеткимимножествами
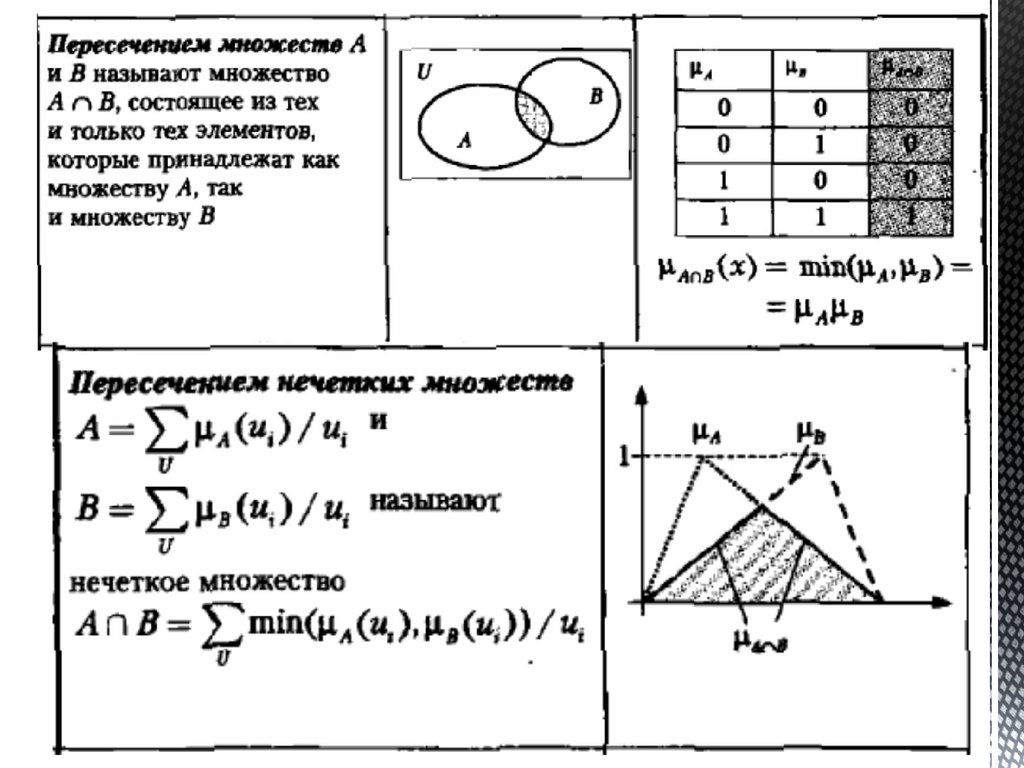
3.
4.
5.
6.
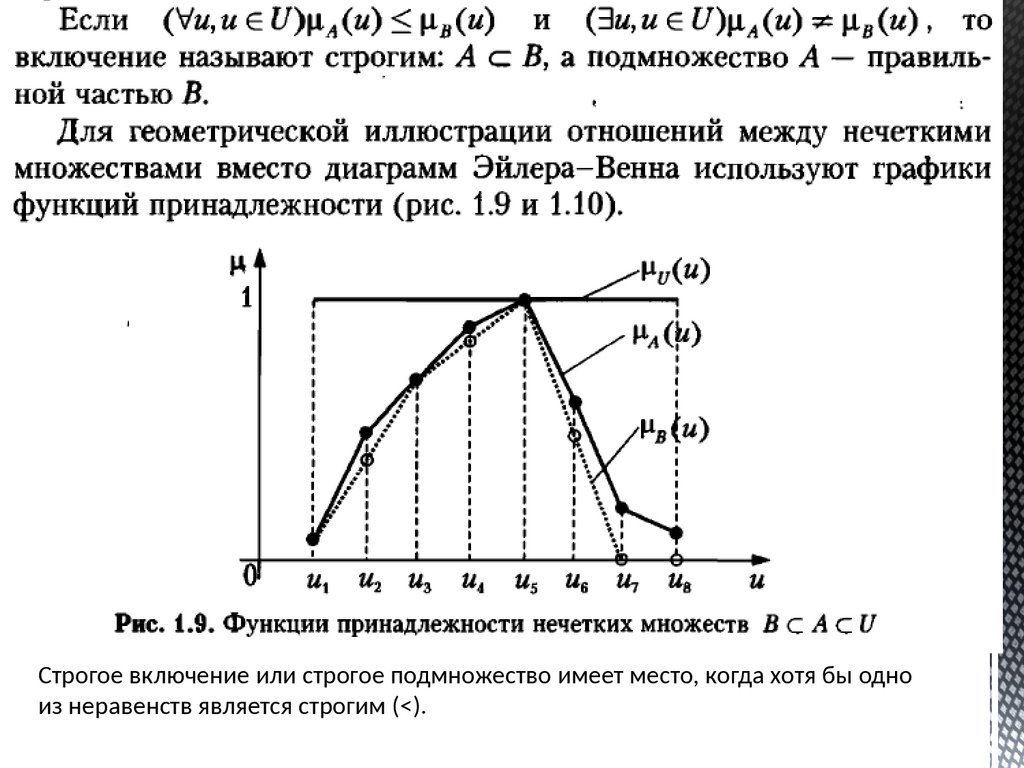
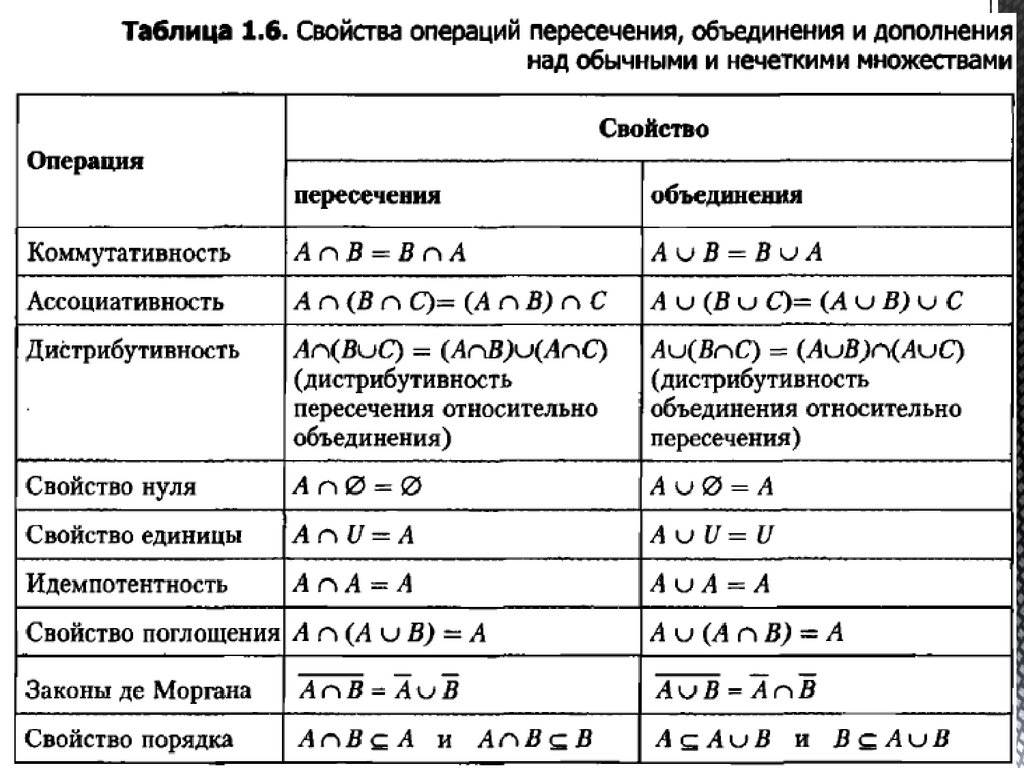
Строгое включение или строгое подмножество имеет место, когда хотя бы одноиз неравенств является строгим (<).
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
6. Синтез нечетких систем25.
Традиционный подход к постановкеи решению задач управления и
регулирования основывается на
предположениях, что модель
объекта управления (ОУ) известна
На практике – математические
модели ОУ очень сложные….
26.
Система управления/диагностики:1. Объект управления
2. Управляемый сигналы (на
которые можно оказывать
воздействие)
3. Измеряемые сигналы
4. Воздействия внешней среды
27.
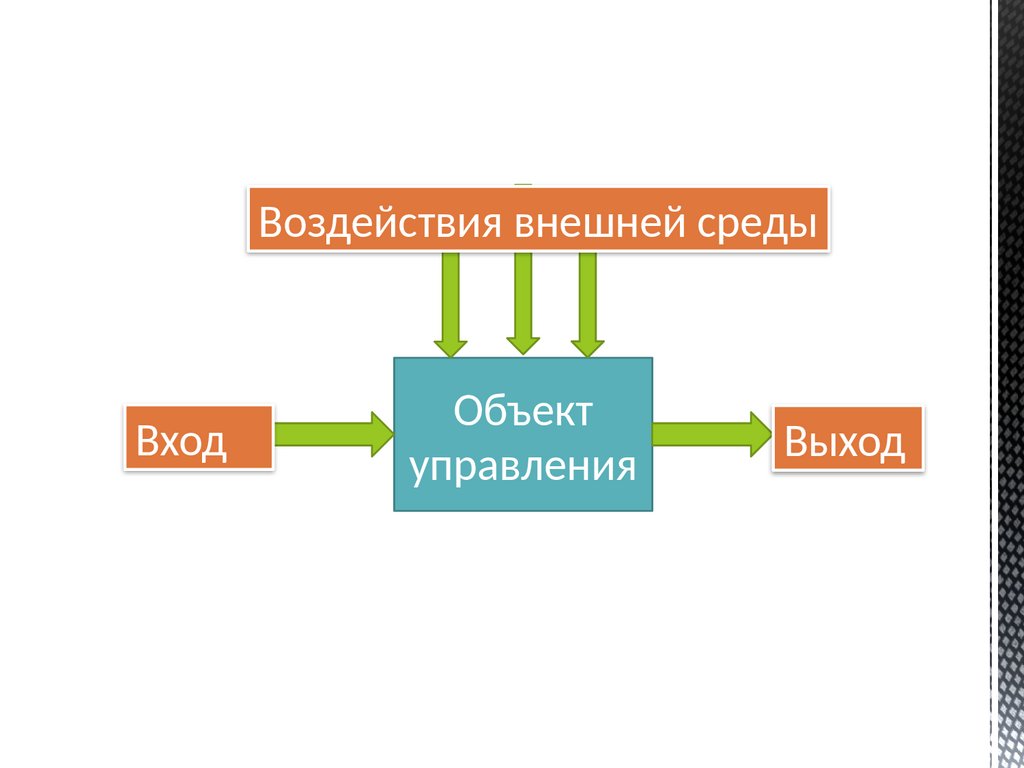
Воздействия внешней средыВход
Объект
управления
Выход
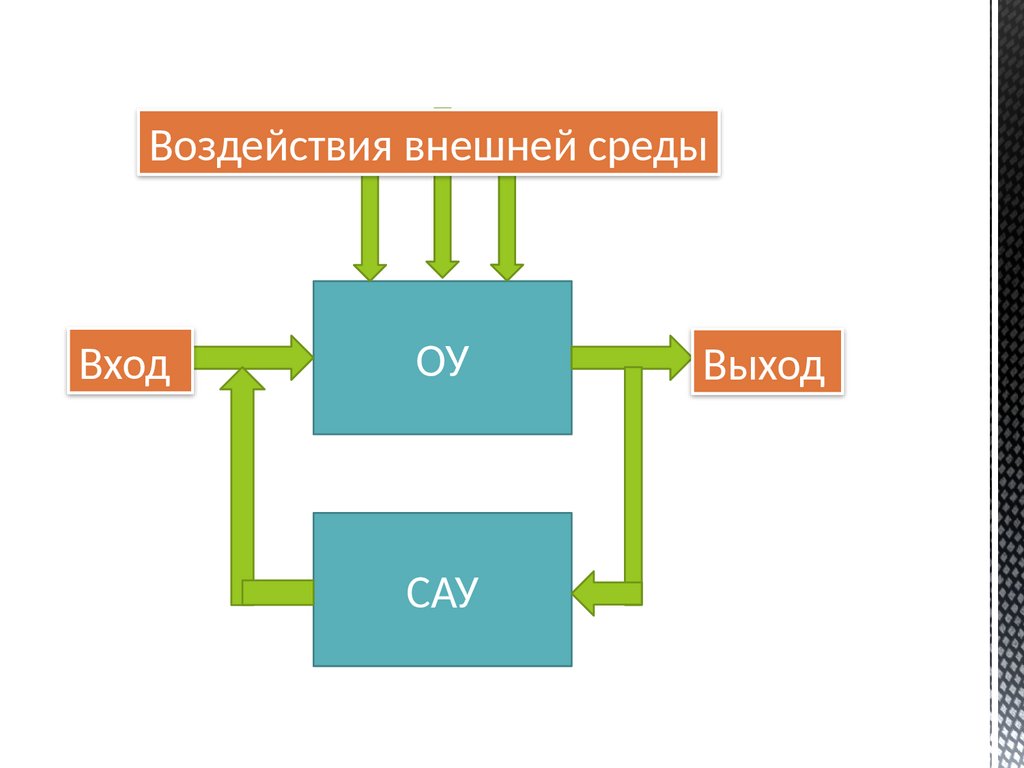
28.
Воздействия внешней средыВход
ОУ
САУ
Выход
29.
Для того чтобы произвести синтезнечеткой системы надо знать 1-4.
И как зависят управляемый сигнал от
измеряемых в виде правил
ЕСЛИ …. И … И …. , ТО
30.
Для того, чтобы сформулировать правилавида
ЕСЛИ …. И … И …. , ТО
Необходимо определить все возможные
состояния для каждого измеряемого
параметра.
31.
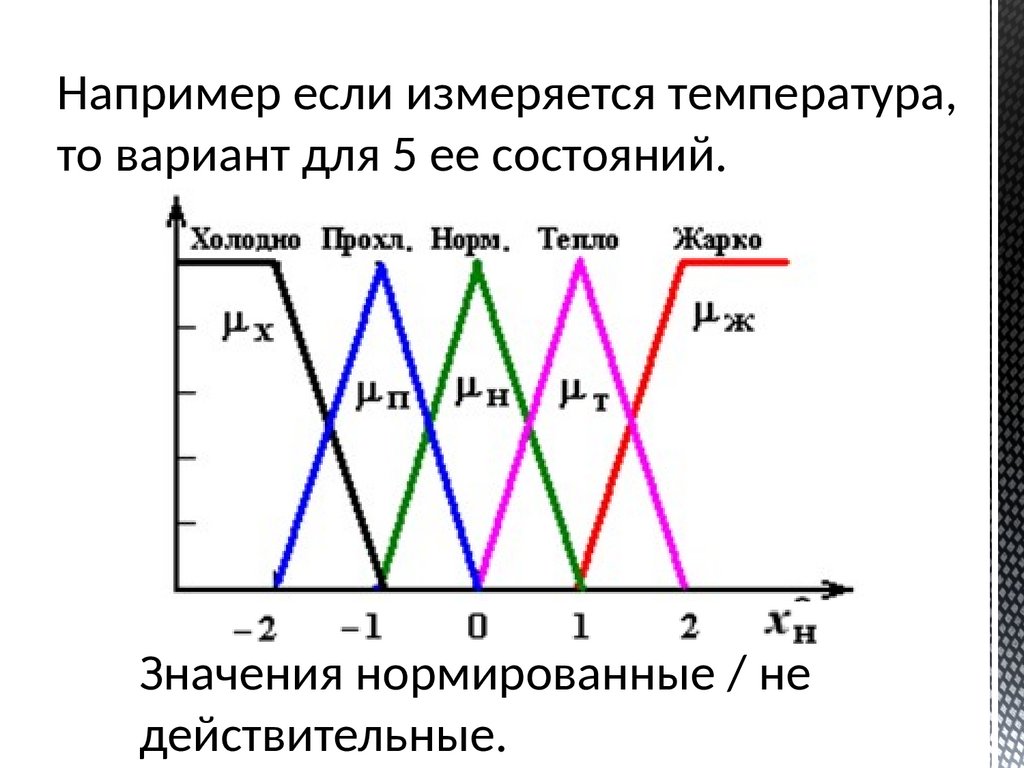
Например если измеряется температура,то вариант для 5 ее состояний.
Значения нормированные / не
действительные.
32.
Варианты возможных состояний:negative big (NB),
negative medium (NM),
negative small (NS),
zero (ZR),
positive small (PS),
positive medium (PM),
positive big (PВ)
Количество состояний может быть:
3, 5, 7, 9
33.
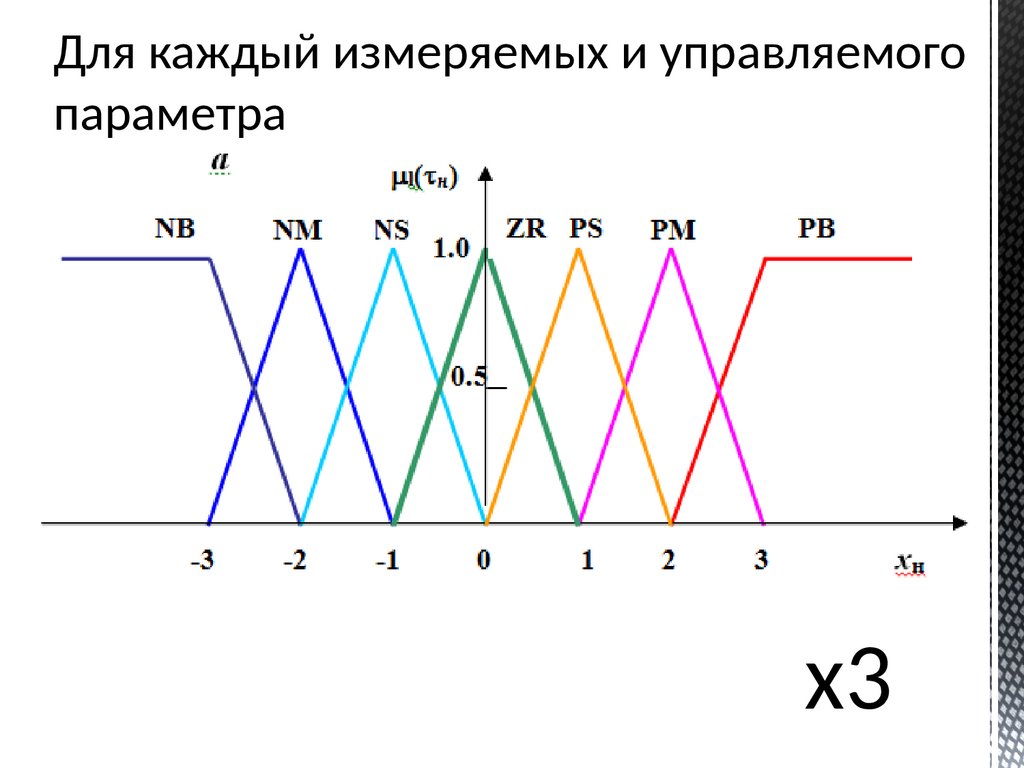
Для каждый измеряемых и управляемогопараметра
x3
34.
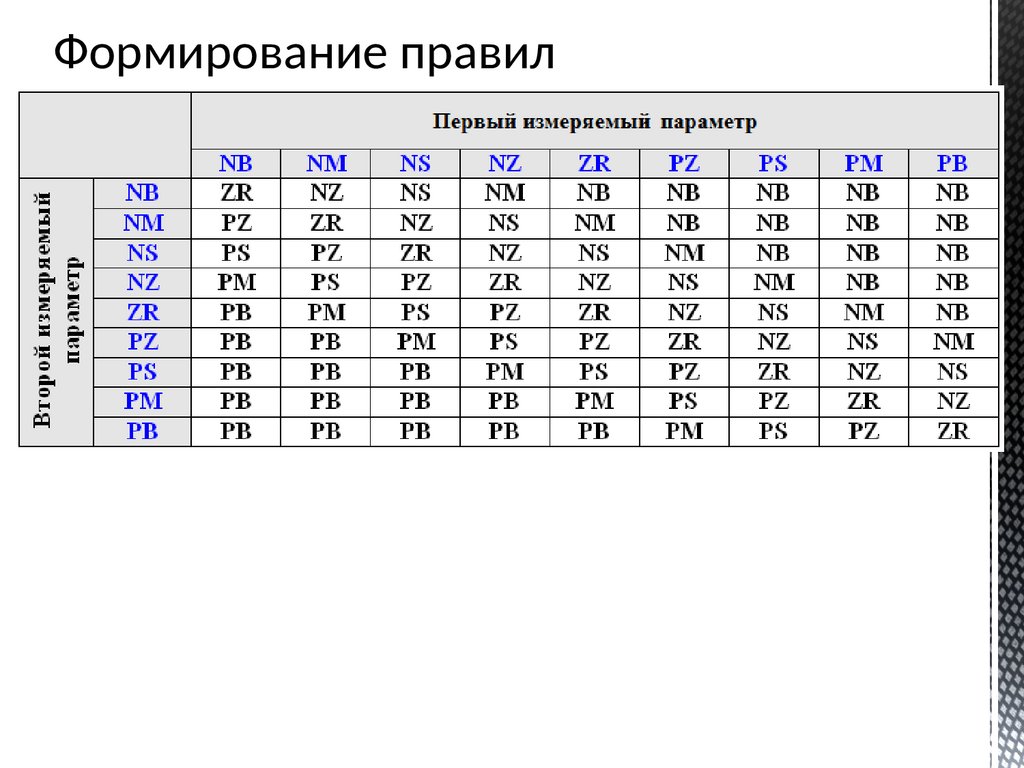
Формирование правил35.
1. Фаззификация2. Расчет нечеткого выхода по базе
нечетких правил
3. Дефаззификация
Эти три оператора зависит от выбранного
алгоритма (Larsen, Mamdani, )
36.
7. Нечеткие илингвистические
переменные
37.
Понятие нечеткой и лингвистическойпеременных используется при
описании объектов и явлений с
помощью нечетких множеств.
38.
Нечеткая переменная характеризуетсятройкой (α, X, А),где
α — наименование переменной;
X — универсальное множество (область
определения α);
А — нечеткое множество на X, описывающее
ограничения (т.е. μA(x))на значения нечеткой
переменной α.
39.
Лингвистическойпеременной (ЛП)называется набор (β, Т, X, G, М), где
β — наименование лингвистической
переменной;
Т — множество ее значений (терммножество), представляющих собой
наименования нечетких переменных,
областью определения каждой из которых
является множество X.
Множество Т называется базовым терммножеством лингвистической
переменной;
40.
G — синтаксическая процедура, позволяющаяоперировать элементами терм-множества T, в
частности, генерировать новые термы
(значения). Множество T∪G(T), где G(T) —
множество сгенерированных термов,
называется расширенным терм-множеством
лингвистической переменной;
М — семантическая процедура, позволяющая
превратить каждое новое значение
лингвистической переменной, образуемое про
цедурой G, в нечеткую переменную, т.е.
сформировать соответствующее нечеткое
множество.
41.
Общепринятые упрощения1) символ β используют как для названия
самой переменной, так и для всех ее
значений;
2) пользуются одним и тем же символом
для обозначения нечеткого множества и
его названия, например терм «Молодой»,
являющийся значением лингвистической
переменной β = «возраст», одновременно
есть и нечеткое множество М(«Молодой»).
42.
Пример. Пусть эксперт определяеттолщину выпускаемого изделия с
помощью понятий «Малая толщина»,
«Средняя толщина» и «Большая толщина»,
при этом минимальная толщина равна 10
мм, а максимальная – 80 мм.
Формализация такого описания может
быть проведена с помощью следующей
лингвистической переменной (β, Т, X, G, М)
43.
β — толщина изделия;Т — {«Малая толщина», «Средняя толщина»,
«Большая толщина»};
X — [10, 80];
G — процедура образования новых термов с
помощью связок «и», «или» и модификаторов
типа «очень», «не», «слегка» и т.п. Например:
«Малая или средняя толщина», «Очень малая
толщина» и т.д.;
44.
М — процедура задания на X = [10, 80]нечетких подмножеств А1 = «Малая
толщина», А2= «Средняя толщина», A3 =
«Большая толщина», а также нечетких
множеств для термов из G(Т)в
соответствии с правилами трансляции
нечетких связок и модификаторов «и»,
«или», «не», «очень», «слегка» и других
операций над нечеткими множествами
вида: А⋂В, A∪В, ̅A,CONА = A2, DILА = А0,5и
т. п.
45.
Наряду с рассмотренными вышебазовыми значениями лингвистической
переменной «Толщина» (Т = {«Малая
толщина», «Средняя толщина», «Большая
толщина»}) возможны значения, завися
щие от области определения X. В данном
случае значения лингвистической
переменной «Толщина изделия» могут
быть определены как «около 20 мм»,
«около 50 мм», «около 70 мм», т.е. в виде
нечетких чисел.
46.
Терм-множество и расширенное терммножество в условиях примера можнохарактеризовать функциями
принадлежности, приведенными на
рисунке на следующих слайдах
47.
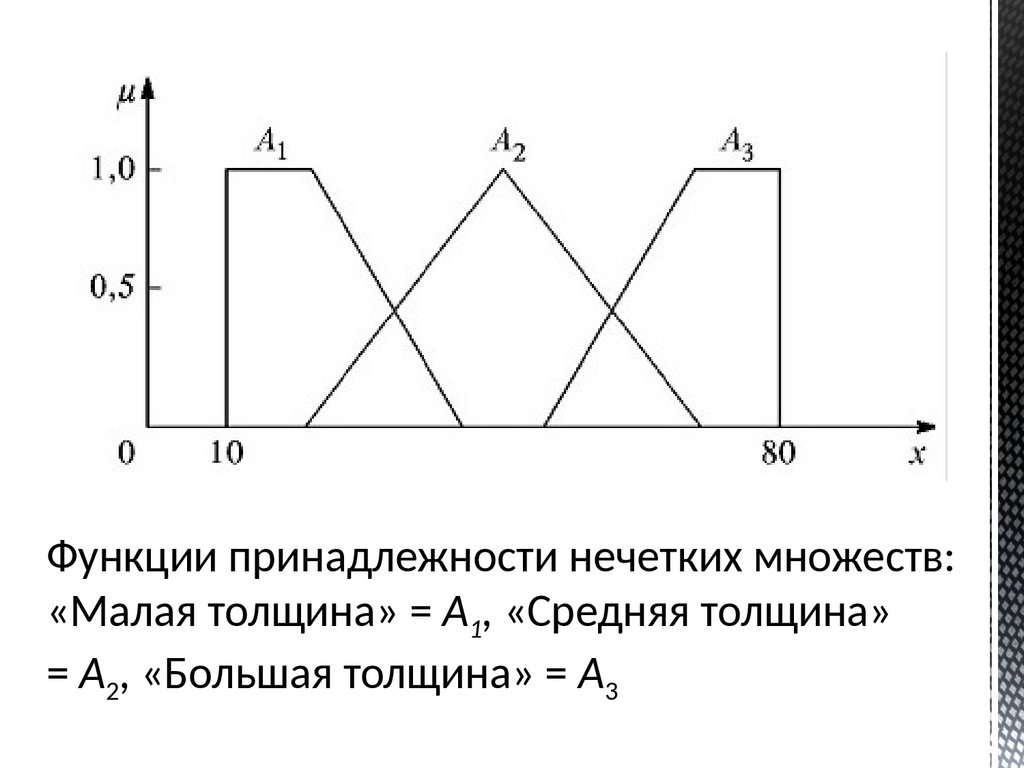
Функции принадлежности нечетких множеств:«Малая толщина» = А1, «Средняя толщина»
= А2, «Большая толщина» = А3
48.
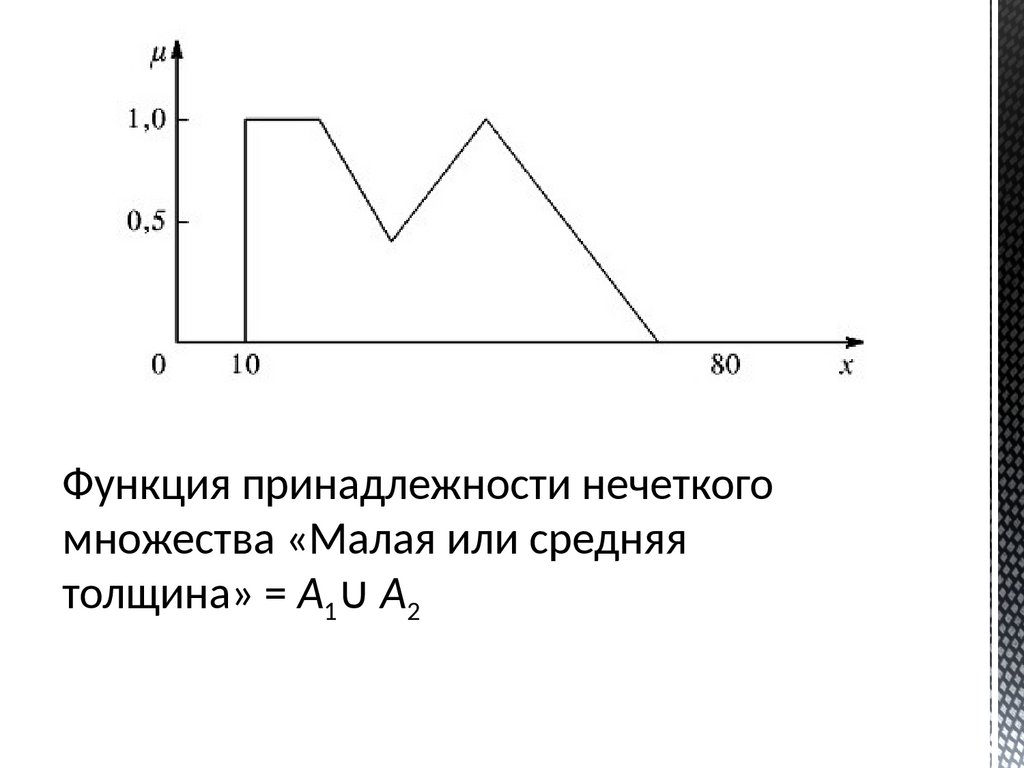
Функция принадлежности нечеткогомножества «Малая или средняя
толщина» = A1∪ А2
49.
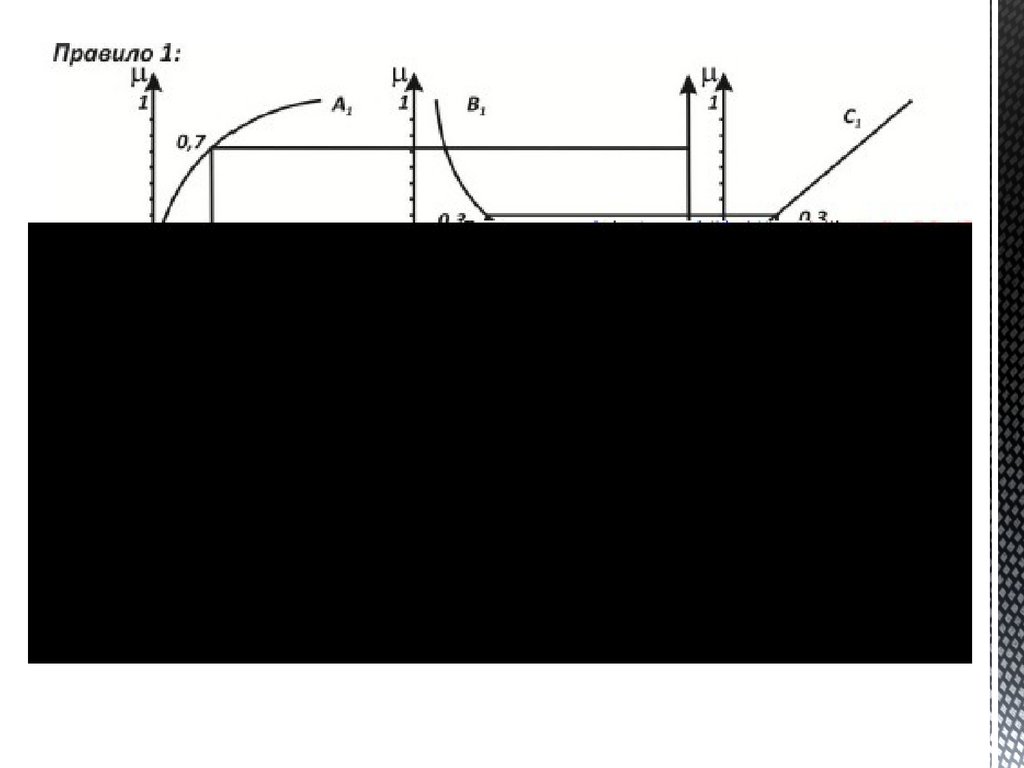
1. Фаззификация2. Расчет нечеткого выхода по базе
нечетких правил
3. Дефаззификация
Эти три оператора зависит от выбранного
алгоритма (Larsen, Mamdani, )
Go to слайд 151
50.
Операции над нечеткими числами.Расширенные бинарные арифметические
операции (сложение, умножение и др.) для
нечетких чисел определяются через
соответствующие операции для четких
чисел с использованием принципа
обобщения следующим образом.



















































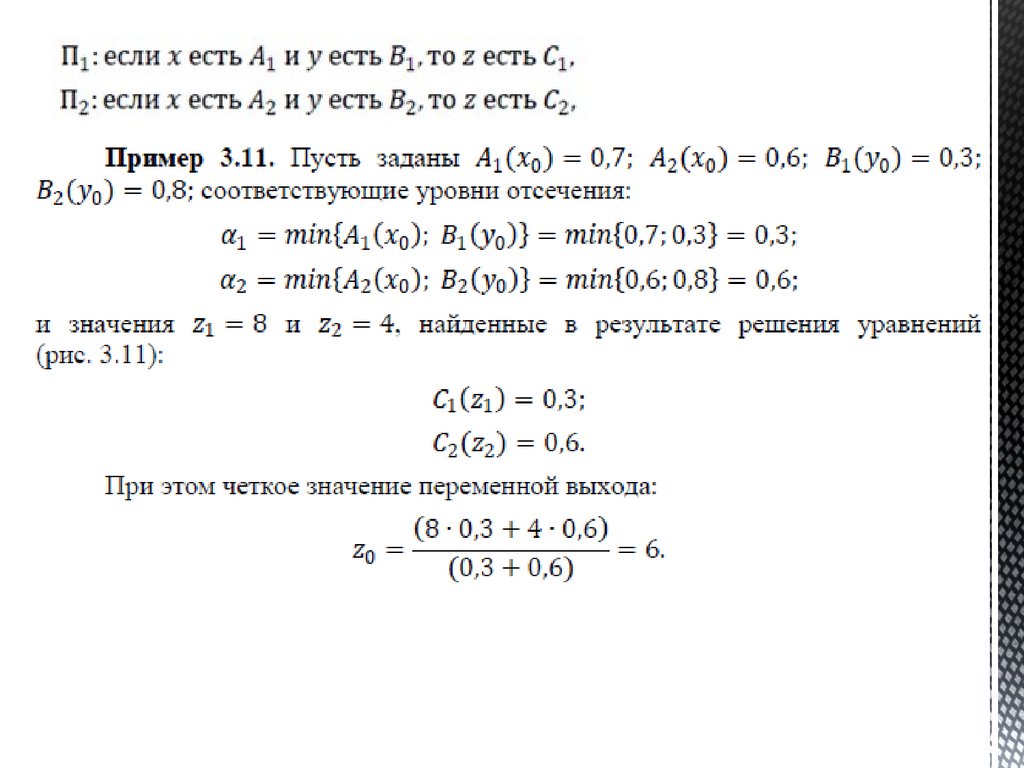

 mathematics
mathematics








