Тела вращения ( лекция)

1. Тела вращения

1

2.

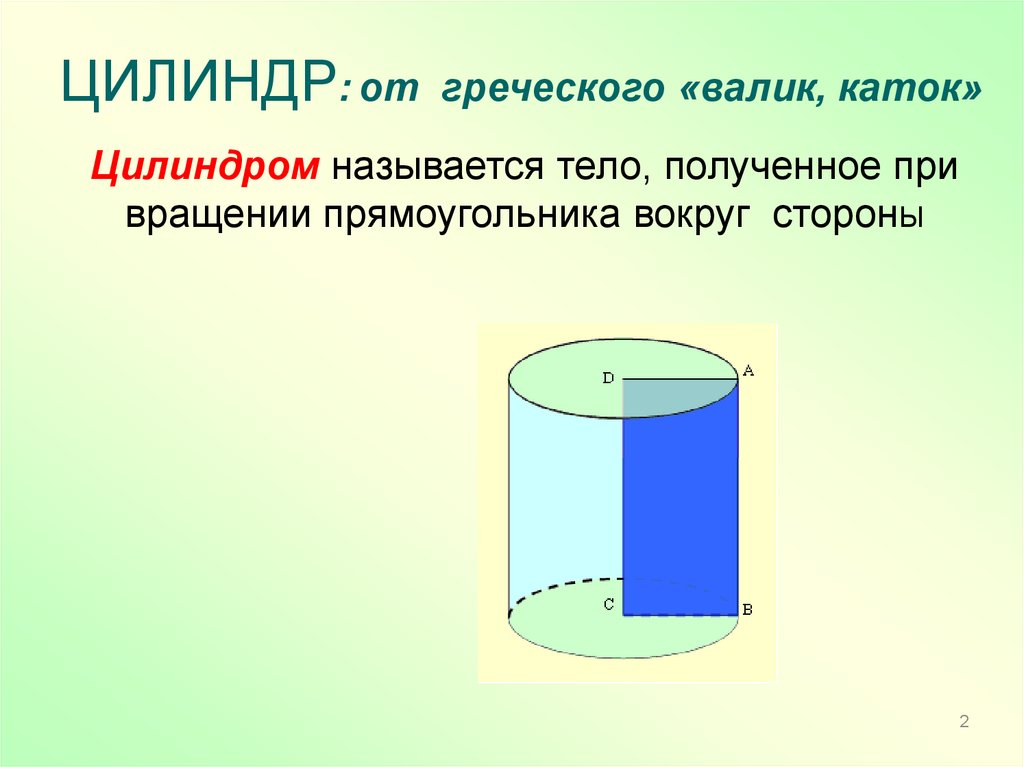
ЦИЛИНДР: от греческого «валик, каток»
Цилиндром называется тело, полученное при
вращении прямоугольника вокруг сторонЫ
2

3.

Основные определения
Основаниями цилиндра являются круги,
O1
Образующими цилиндра называются отрезки,
соединяющие соответствующие точки
окружностей кругов ( обозначаются L)
Н
O
R
Радиусом цилиндра называется радиус его
основания ( R)
Высотой цилиндра называется расстояние между плоскостями
оснований ( H)
Осью цилиндра называется прямая, проходящая через центры
оснований.
3

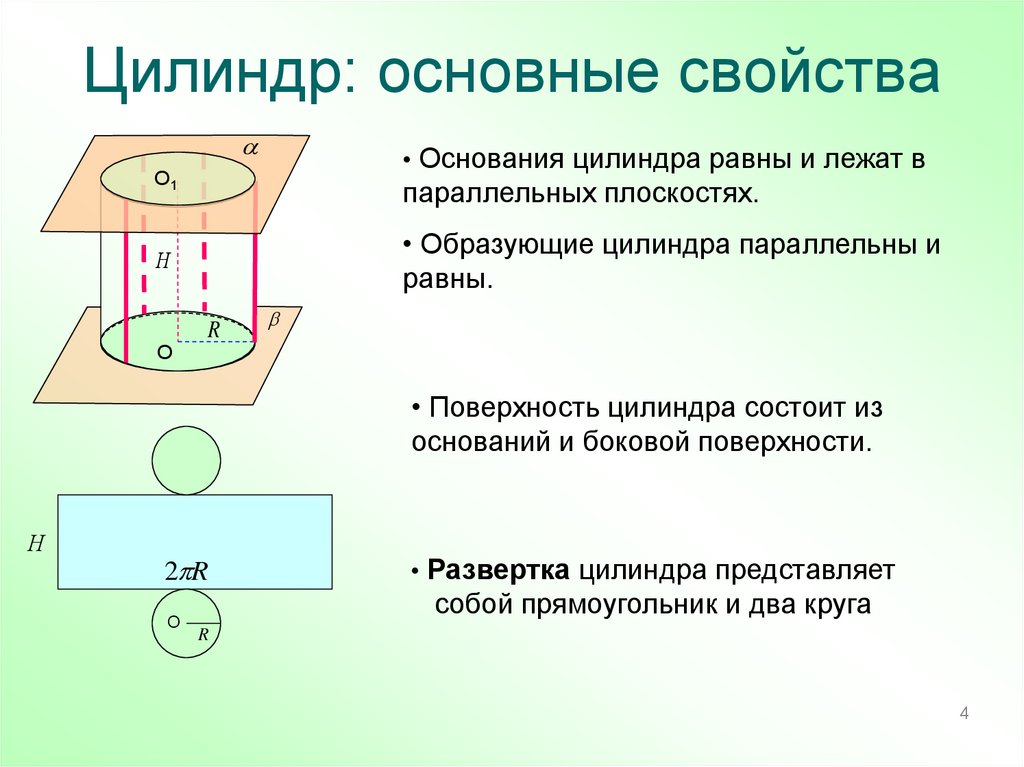
4. Цилиндр: основные свойства

• Основания цилиндра равны и лежат в
O1
параллельных плоскостях.
• Образующие цилиндра параллельны и
равны.
Н
R
O
• Поверхность цилиндра состоит из
оснований и боковой поверхности.
Н
2 R
O
• Развертка цилиндра представляет
собой прямоугольник и два круга
R
4

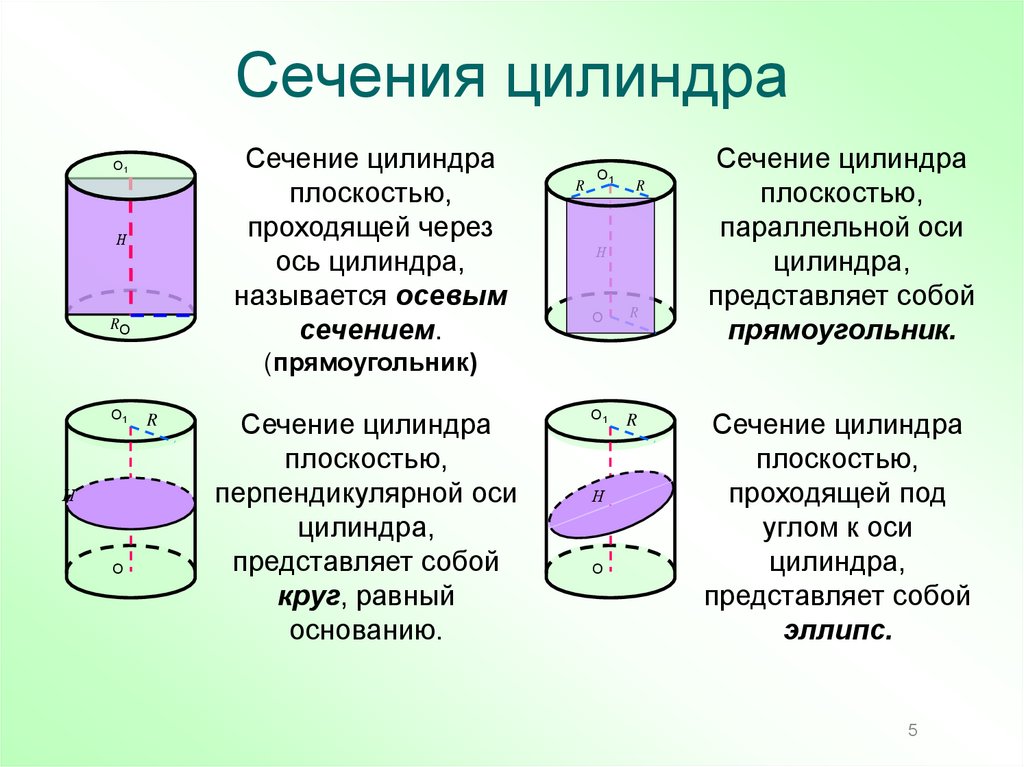
5. Сечения цилиндра

Сечение цилиндра
плоскостью,
проходящей через
ось цилиндра,
называется осевым
сечением.
O1
Н
RO
R
O1
R
Н
O
R
O1
R
Сечение цилиндра
плоскостью,
параллельной оси
цилиндра,
представляет собой
прямоугольник.
(прямоугольник)
O1
Н
O
R
Сечение цилиндра
плоскостью,
перпендикулярной оси
цилиндра,
представляет собой
круг, равный
основанию.
Н
O
Сечение цилиндра
плоскостью,
проходящей под
углом к оси
цилиндра,
представляет собой
эллипс.
5

6.

КОНУС: от греческого «сосновая шишка,
остроконечная верхушка шлема»
Конусом называется тело, полученное при
вращении прямоугольного треугольника вокруг
катета
6

7.

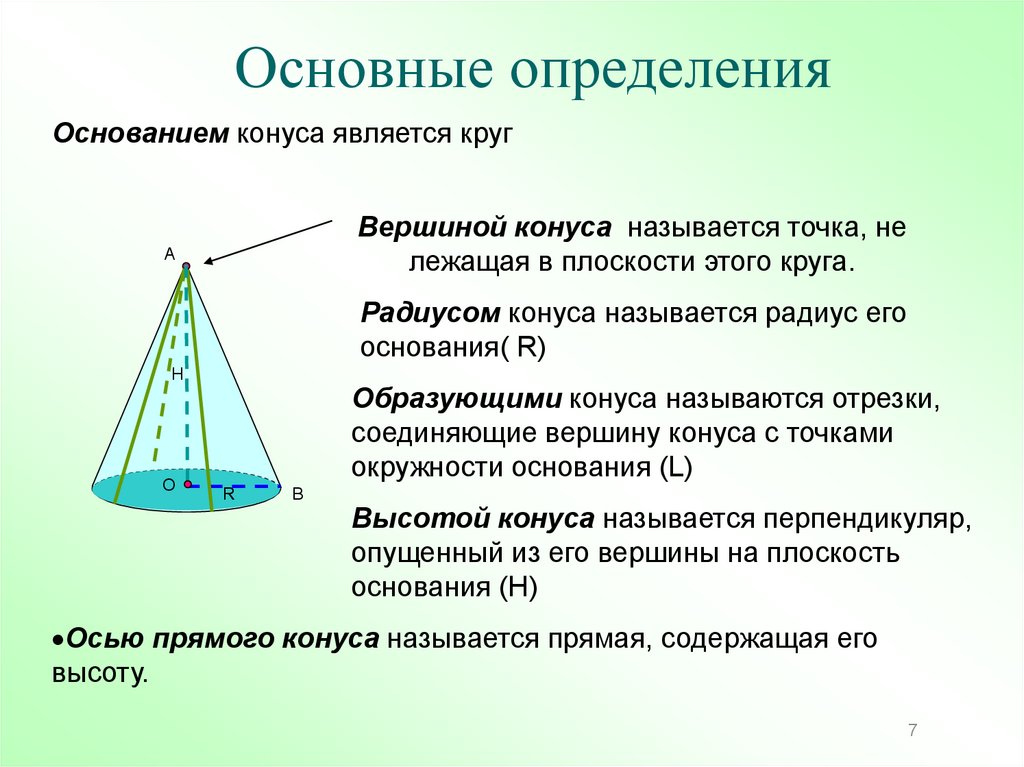
Основные определения
Основанием конуса является круг
Вершиной конуса называется точка, не
лежащая в плоскости этого круга.
А
Радиусом конуса называется радиус его
основания( R)
Н
О
Образующими конуса называются отрезки,
соединяющие вершину конуса с точками
окружности основания (L)
R
В
Высотой конуса называется перпендикуляр,
опущенный из его вершины на плоскость
основания (H)
Осью прямого конуса называется прямая, содержащая его
высоту.
7

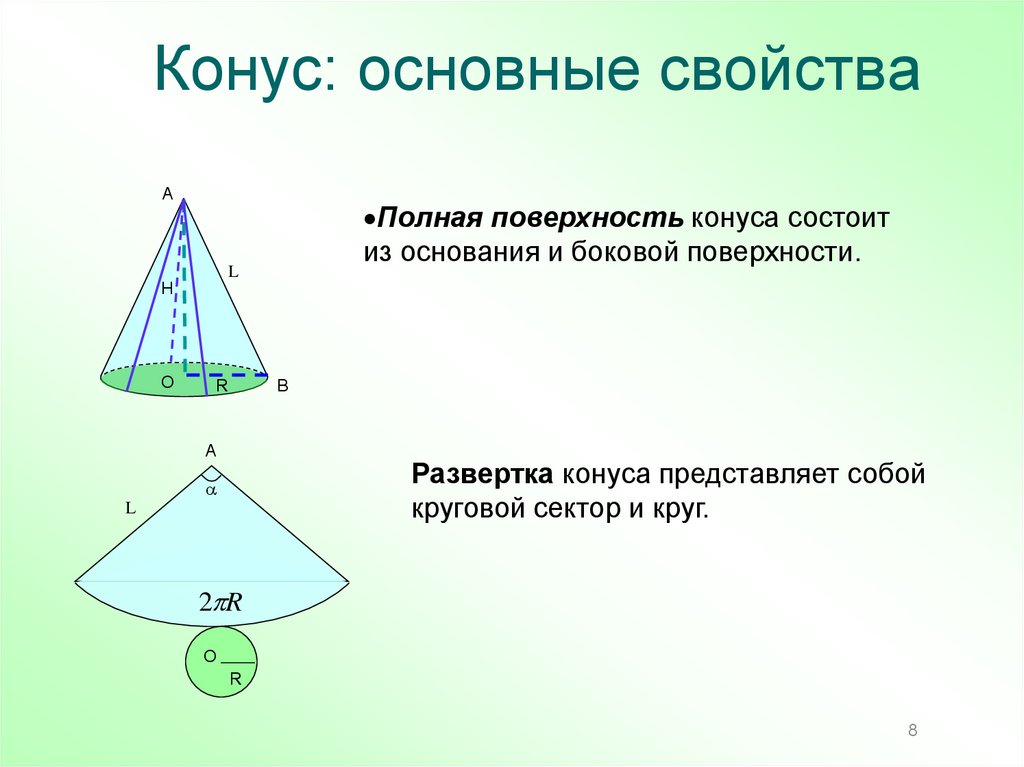
8. Конус: основные свойства

А
L
Н
О
Полная поверхность конуса состоит
из основания и боковой поверхности.
В
R
А
Развертка конуса представляет собой
круговой сектор и круг.
L
2 R
О
R
8

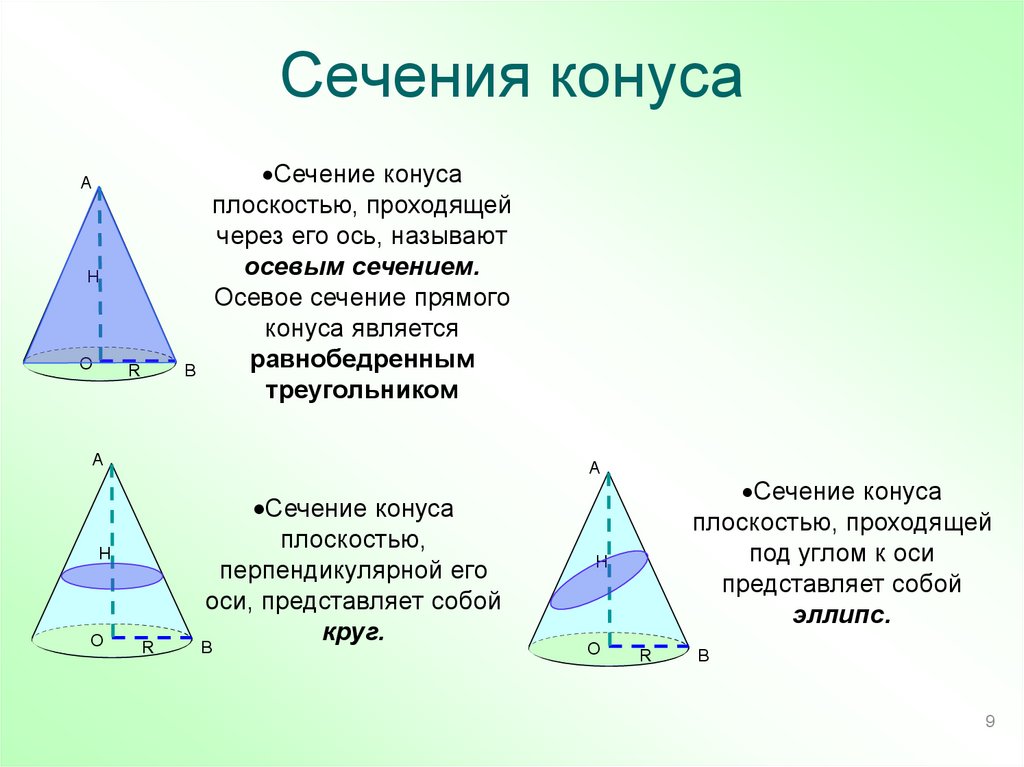
9. Сечения конуса

Сечение конуса
плоскостью, проходящей
через его ось, называют
осевым сечением.
Осевое сечение прямого
конуса является
равнобедренным
В
треугольником
А
Н
О
R
А
А
Н
О
R
Сечение конуса
плоскостью,
перпендикулярной его
оси, представляет собой
круг.
В
Сечение конуса
плоскостью, проходящей
под углом к оси
представляет собой
эллипс.
Н
О
R
В
9

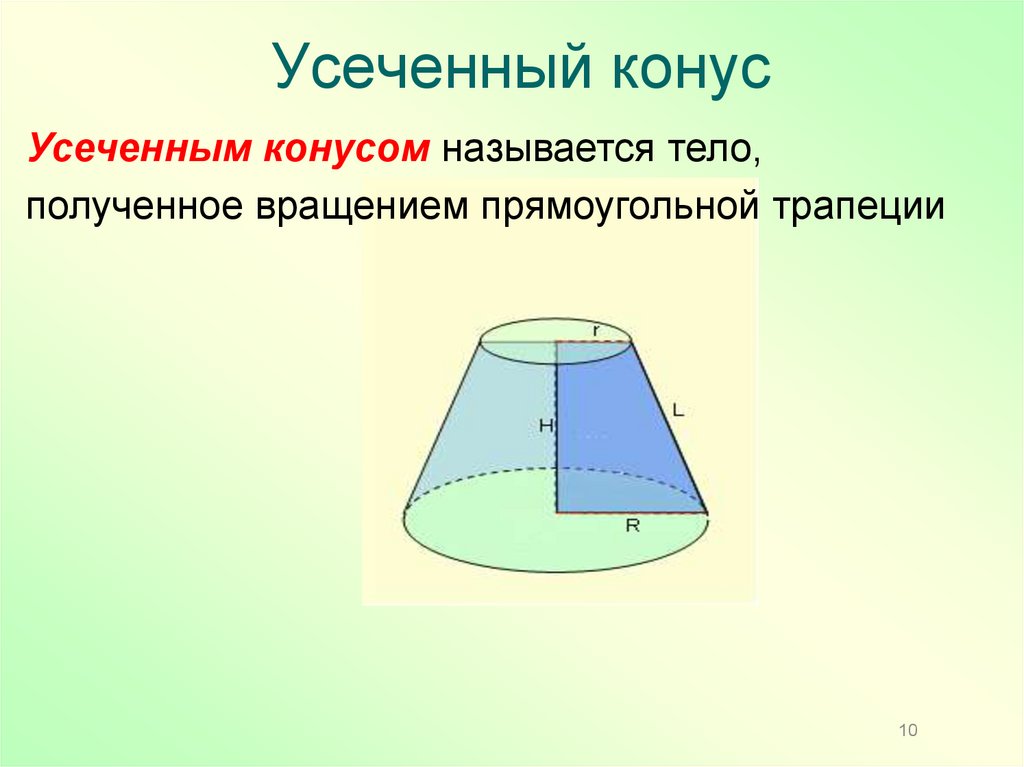
10. Усеченный конус

Усеченным конусом называется тело,
полученное вращением прямоугольной трапеции
10

11.

Основные определения
Основаниями усеченного конуса являются круги.
r
L
Н
R
Образующими называются отрезки,
расположенные между основаниями усеченного
конуса ( L)
Радиусами усеченного конуса называются радиусы его оснований ( R и r).
Высотой называется отрезок, соединяющий центры оснований
усеченного конуса (H)
11

12.

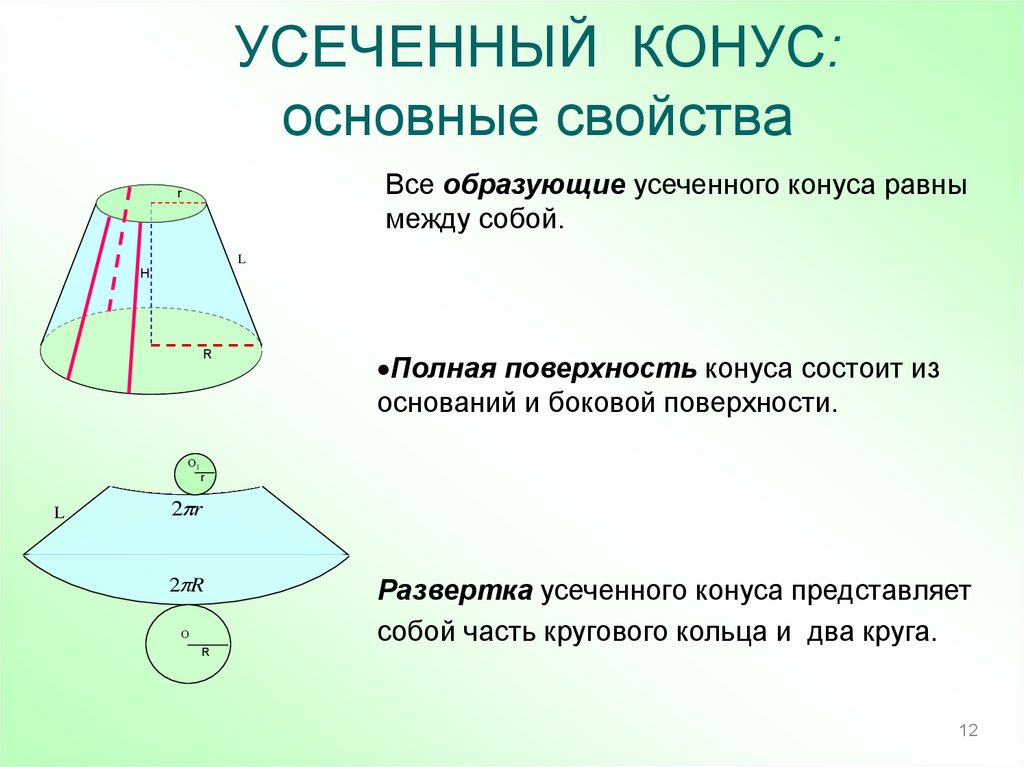
УСЕЧЕННЫЙ КОНУС:
основные свойства
Все образующие усеченного конуса равны
между собой.
r
L
Н
R
Полная поверхность конуса состоит из
оснований и боковой поверхности.
О1
r
L
2 r
2 R
О
Развертка усеченного конуса представляет
собой часть кругового кольца и два круга.
R
12

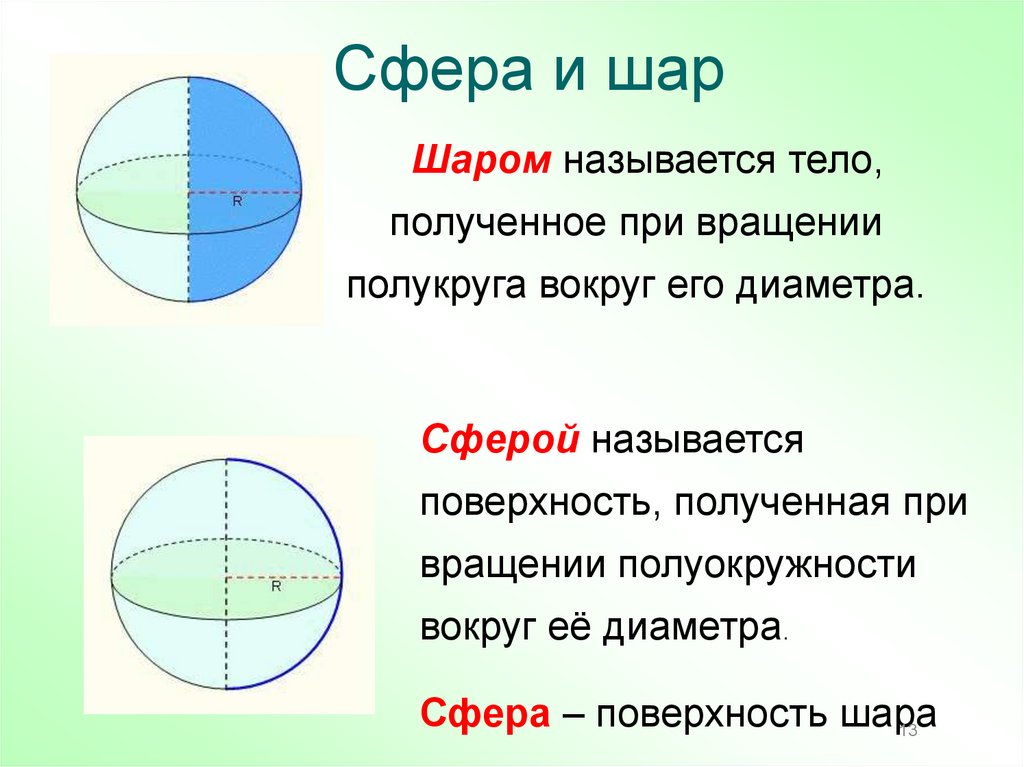
13. Сфера и шар

сфера
Шаром называется тело,
полученное при вращении
полукруга вокруг его диаметра.
Сферой называется
поверхность, полученная при
вращении полуокружности
вокруг её диаметра.
Сфера – поверхность шара
13

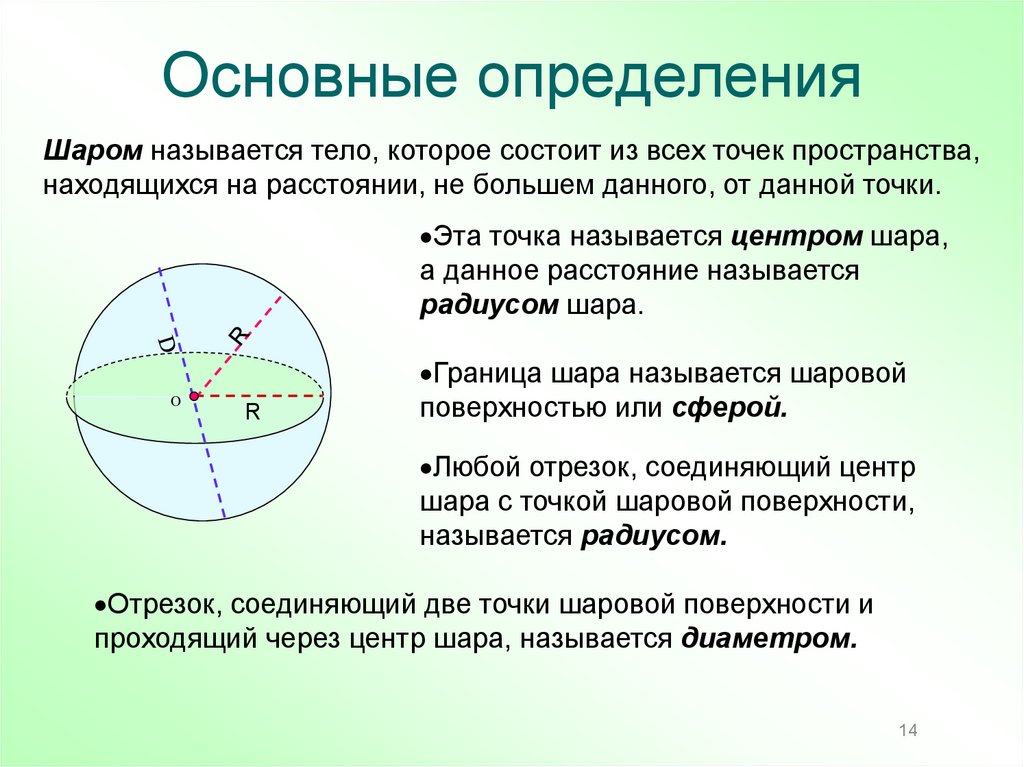
14. Основные определения

Шаром называется тело, которое состоит из всех точек пространства,
находящихся на расстоянии, не большем данного, от данной точки.
Эта точка называется центром шара,
а данное расстояние называется
радиусом шара.
O
R
R
Граница шара называется шаровой
поверхностью или сферой.
Любой отрезок, соединяющий центр
шара с точкой шаровой поверхности,
называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и
проходящий через центр шара, называется диаметром.
14

15.

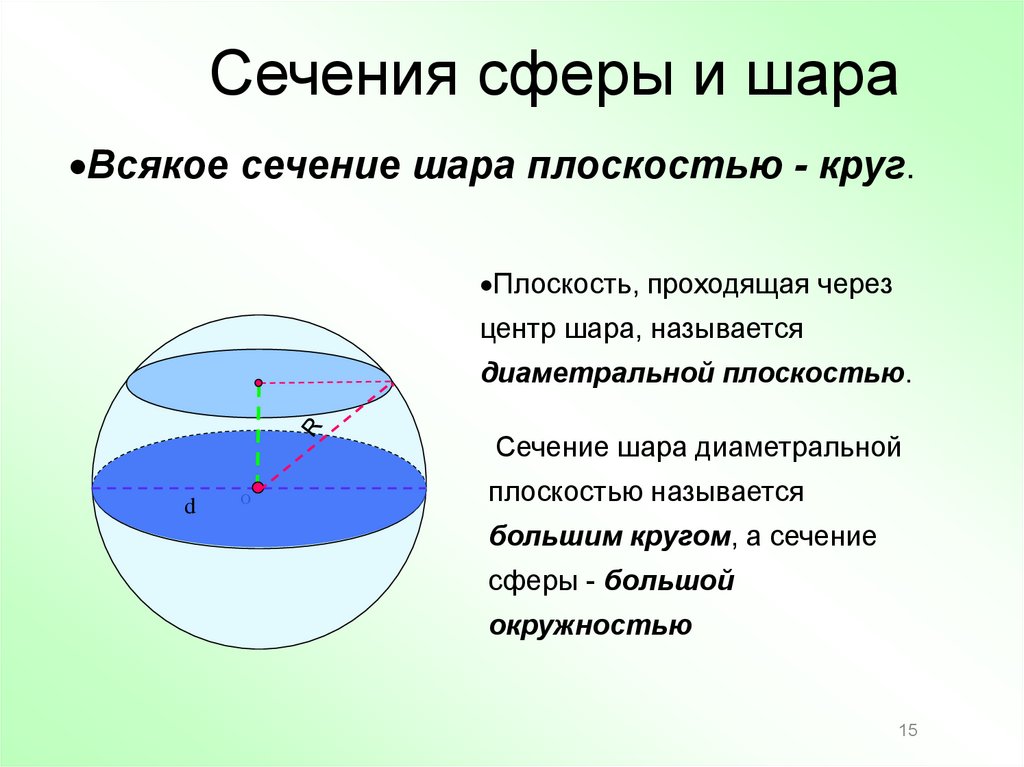
Сечения сферы и шара
Всякое сечение шара плоскостью - круг.
Плоскость, проходящая через
центр шара, называется
диаметральной плоскостью.
Сечение шара диаметральной
d
плоскостью называется
O
большим кругом, а сечение
R
сферы - большой
окружностью
15

16.

Формулы площади поверхности и
объема тел вращения
Название
тела
Формула
Формула
площади бок. площади полной
поверхности
поверхности
Формула
объема
Цилиндр
S бок 2 RH
S 2 R( H R )
V R 2 H
Конус
S бок RL
S R( L R )
Усеченный
конус
S бок L( R r )
S L( R r )
1
V R 2 H
3
Шар (V),
Сфера(S)
1
2
V Н ( R Rr r 2 )
3
R 2 r 2
S 4 R d
2
2
4
1
V R 3 d 3
3
6
16