Ispolzovanie_grafov_i_derevyev_pri_opisanii_obektov_i__kopia

1. Использование графов и деревьев при описании объектов и процессов окружающего мира

2.

ПОВТОРИМ
Коды бывают равномерными (кодовые слова имеют
одинаковую длину) и неравномерными (кодовые слова имеют
разную длину). Неравномерные коды
позволяют сократить
среднюю длину кодового слова, тем самым уменьшив объем
информации, необходимый для передачи сообщения. Однако при
использовании
неравномерных
кодов
возникает
проблема
разделения кодовых слов в сообщении, так как неизвестно, где
заканчивается одно слово и начинается другое. Для решения этой
проблемы можно использовать разделители между кодовыми
словами или построить так называемые разделимые (префиксные)
коды.
Для
обеспечения
однозначного
и
правильного
декодирования сообщения без использования разделителей
используют префиксный (неравномерный)код, удовлетворяющий
условию Фано.

3.

Префиксный код — это неравномерный код, который
удовлетворяет условию Фано.
По условию Фано никакое кодовое слово не должно
быть началом никакого другого кодового слова.
Одним из способов построения оптимальных префиксных
кодов является метод Хаффмана, в котором используется
двоичное дерево (связный граф, в котором каждая вершина имеет
не более двух смежных вершин). Метод Хаффмана заключается в
том, что по заданному алфавиту и вероятностям появления его
символов в сообщении строится двоичное дерево, в котором
листья соответствуют символам используемого алфавита. Ребра
между метками помечают символами 0 или 1. Кодовое слово для
каждого символа получается путем записи меток на ребрах, от
корня дерева до соответствующего листа. Такой метод гарантирует
минимальную среднюю длину кодового слова для данного
алфавита.

4.

Задание 1.
По каналу связи передаются сообщения, содержащие
только пять букв: А, Б, В, Г, Д. Для передачи используется
неравномерный двоичный код, удовлетворяющий условию Фано.
Кодовые слова для некоторых букв известны: А — 0, Б — 10, В —
110. Укажи кодовое слово, которое можно использовать для буквы
Г. Слово должно быть наименьшей возможной длины. Если таких
слов несколько, укажи то из них, которое соответствует
наименьшему возможному двоичному числу.
Решение.
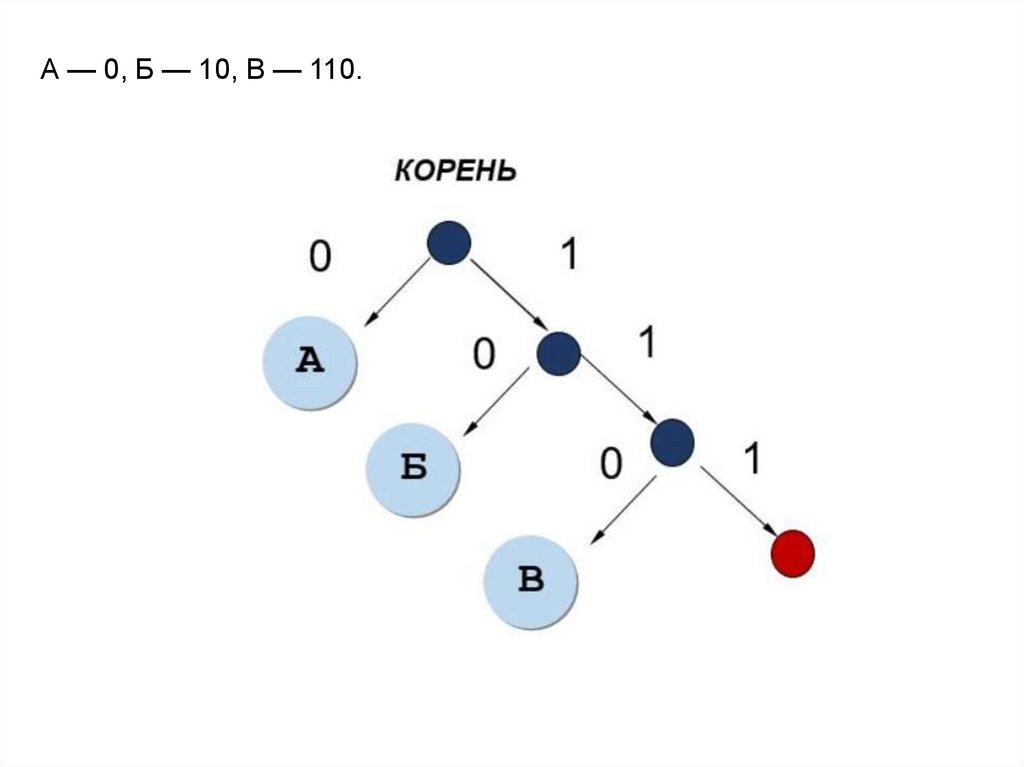
Построим код Хаффмана для букв А, Б и В:

5.

А — 0, Б — 10, В — 110.

6.

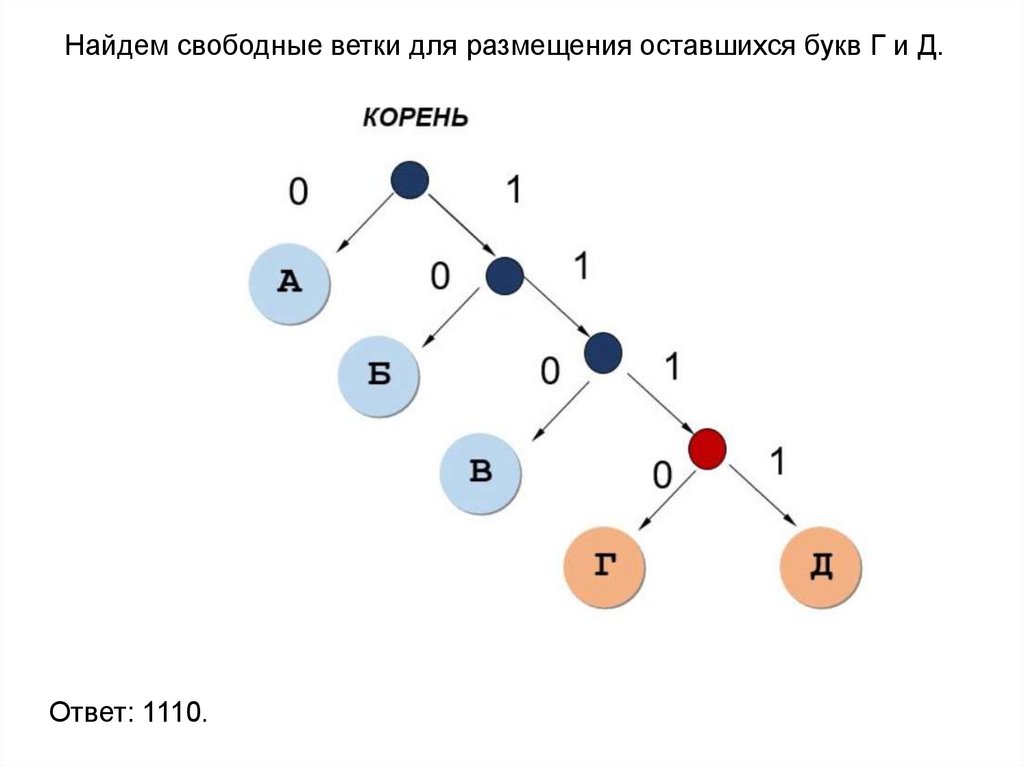
Найдем свободные ветки для размещения оставшихся букв Г и Д.
Ответ: 1110.

7.

Задание 3.
Известна частота следующих букв
Используя алгоритм Хаффмана, найдите кодовые слова
данных букв.

8.

Задача 1. По каналу связи передаются сообщения, содержащие
только четыре буквы: А, Б, В, Г. Для передачи используется
неравномерный двоичный код, удовлетворяющий условию Фано.
Кодовые слова для некоторых букв известны: А — 0, Б — 10. Построй
граф Хаффмана для этого кода и определи кодовые слова для
букв В и Г.
Задача 2. По каналу связи передаются сообщения, содержащие
только пять букв: А, Б, В, Г, Д. Для передачи используется
неравномерный двоичный код, удовлетворяющий условию Фано, где
кодовые слова для всех букв известны: А — 0, Б — 10, В — 110,
Г — 1110, Д — 1111. Закодируй слово «БАГДАД» и посчитай длину
получившейся строки.
Задача 3. Укажи все возможные кодовые слова для буквы В, зная,
что по каналу связи передаются сообщения, содержащие только пять
букв: А, Б, В, Г, Д. Для передачи используется неравномерный
двоичный код. Кодовые слова для некоторых букв известны: А — 0,
Б — 10.