Similar presentations:
Алгоритмы сжатия текстовых, числовых и табличных данных
1. Алгоритмы сжатия текстовых, числовых и табличных данных
АЛГОРИТМЫ СЖАТИЯТЕКСТОВЫХ, ЧИСЛОВЫХ И
ТАБЛИЧНЫХ ДАННЫХ
2. Основные определения
ОСНОВНЫЕОПРЕДЕЛЕНИЯ
3. Сжатие данных
◦ Сжатие данных – это процесс, обеспечивающий уменьшение объемаданных путем сокращения их избыточности. Сжатие данных связано с
компактным расположением порций данных стандартного размера. Сжатие
данных можно разделить на два основных типа:
◦ Сжатие без потерь (полностью обратимое) – это метод сжатия данных, при
котором ранее закодированная порция данных восстанавливается после их
распаковки полностью без внесения изменений. Для каждого типа данных,
как правило, существуют свои оптимальные алгоритмы сжатия без потерь.
◦ Сжатие с потерями – это метод сжатия данных, при котором для
обеспечения максимальной степени сжатия исходного массива данных
часть содержащихся в нем данных отбрасывается. Для текстовых, числовых и
табличных данных использование программ, реализующих подобные методы
сжатия, является неприемлемыми. В основном такие алгоритмы применяются
для сжатия аудио- и видеоданных, статических изображений.
4.
◦ Алфавит кода – множество всех символов входного потока. Присжатии англоязычных текстов обычно используют множество из
128 ASCII кодов. При сжатии изображений множество значений
пикселя может содержать 2, 16, 256 или другое количество элементов.
◦ Кодовый символ – наименьшая единица данных, подлежащая
сжатию. Обычно символ – это 1 байт, но он может быть битом, тритом
{0,1,2}, или чем-либо еще.
◦ Кодовое слово – это последовательность кодовых символов из
алфавита кода. Если все слова имеют одинаковую длину (число
символов), то такой код называется равномерным (фиксированной
длины), а если же допускаются слова разной длины, то –
неравномерным (переменной длины).
◦ Код – полное множество слов.
5.
◦ Токен – единица данных, записываемая всжатый поток некоторым алгоритмом сжатия. Токен состоит
из нескольких полей фиксированной или переменной
длины.
◦ Фраза – фрагмент данных, помещаемый в словарь для
дальнейшего использования в сжатии.
◦ Кодирование – процесс сжатия данных.
◦ Декодирование – обратный кодированию процесс, при
котором осуществляется восстановление данных.
6.
.◦ Отношение сжатия – одна из наиболее часто используемых величин
для обозначения эффективности метода сжатия
◦ Значение 0,6 означает, что данные занимают 60% от первоначального
объема. Значения больше 1 означают, что выходной поток больше
входного (отрицательное сжатие, или расширение).
◦ Коэффициент сжатия – величина, обратная отношению сжатия.
Значения больше 1 обозначают сжатие, а значения меньше 1 –
расширение.
7.
◦Средняя длина кодового слова – этовеличина, которая вычисляется как взвешенная
вероятностями сумма длин всех кодовых слов.
Lcp=p1L1+p2L2+...+pnLn,
где – вероятности кодовых слов;
L1,L2,...,Ln – длины кодовых слов.
8. Два основных способа проведения сжатия
◦ Статистические методы – методы сжатия, присваивающие кодыпеременной длины символам входного потока, причем более
короткие коды присваиваются символам или группам символам,
имеющим большую вероятность появления во входном потоке.
Лучшие статистические методы применяют кодирование
Хаффмана.
◦ Словарное сжатие – это методы сжатия, хранящие фрагменты
данных в "словаре" (некоторая структура данных). Если строка
новых данных, поступающих на вход, идентична какому-либо
фрагменту, уже находящемуся в словаре, в
выходной поток помещается указатель на этот фрагмент.
Лучшие словарные методы применяют метод Зива-Лемпела.
9. Примеры и краткая характеристика методов сжатия
◦ 1. Метод кодирования длины серий.◦ 2. Метод кодирования по словарю.
◦ 3. Энтропийное кодирование.
◦ 4. …
◦ Префиксный код – это код, в котором никакое кодовое слово
не является префиксом любого другого кодового слова. Эти
коды имеют переменную длину. Оптимальный префиксный
код – это префиксный код, имеющий минимальную
среднюю длину.
10. Алгоритм Шеннона-Фано
АЛГОРИТМШЕННОНА-ФАНО
11.
◦ Метод Фано делит исходные символы на дванабора ("0" и "1") с вероятностями, максимально
близкими к 1/2. Затем эти наборы сами делятся на
два и так далее, пока каждый набор не будет
содержать только один символ. Кодовым словом для
этого символа является строка из "0" и "1", которая
записывает, на какую половину делений он упал.
◦ Этот метод был предложен в более
позднем техническом отчёте Фано (1949).
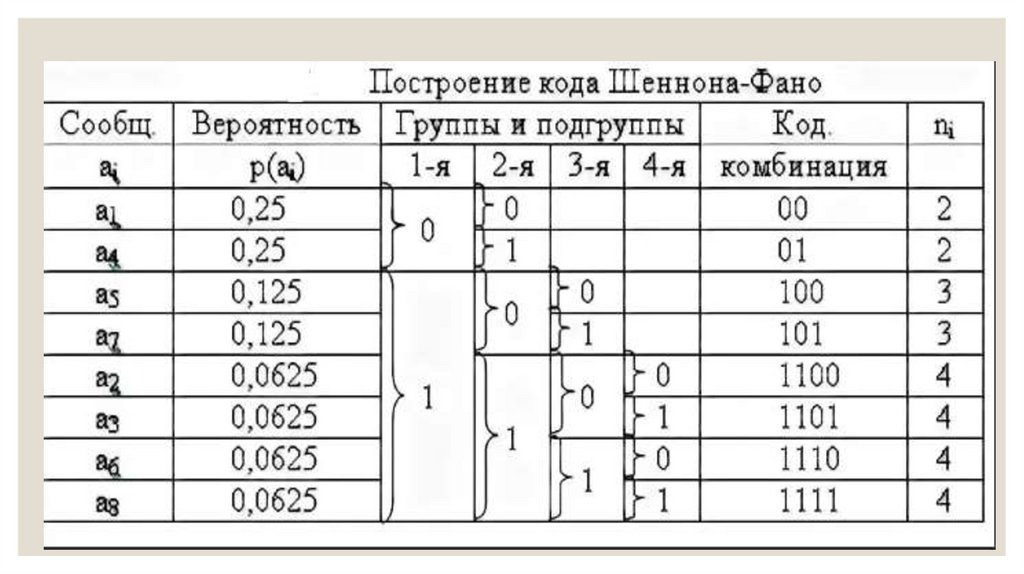
12. Дерево Шеннона–Фано
1. Для заданного списка символов разработайте соответствующийсписок вероятностей или частот, чтобы была известна относительная
частота появления каждого символа.
2. Сортируйте списки символов в соответствии с частотой, с наиболее часто
встречающимися символами слева и наименее распространенными
справа.
3. Разделите список на две части, при этом общее количество частот в левой
части должно быть как можно ближе к общему количеству частот в правой
части.
4. Левой части списка присваивается двоичная цифра 0, а правой части
присваивается цифра 1. Это означает, что все коды для символов в первой
части будут начинаться с 0, а все коды во второй части будут начинаться с 1.
5. Рекурсивно применяйте шаги 3 и 4 к каждой из двух половин, разделяя
группы и добавляя биты к кодам, пока каждый символ не станет
соответствующим листом кода в дереве.
13. Пример
◦ Для заданного списка символов разработайте соответствующийсписок вероятностей или частот, чтобы была известна относительная частота
появления каждого символа.
◦ Сортируйте списки символов в соответствии с частотой, с наиболее часто
встречающимися символами слева и наименее распространенными справа.
◦ Разделите список на две части, при этом общее количество частот в левой части
должно быть как можно ближе к общему количеству частот в правой части.
0.385+0.179=0.564
0.154+0.154+0.128=0.436
При таком разделении каждый из A и B будет иметь код,
начинающийся с бита 0, а все коды C, D и E будут начинаться с 1
14.
◦ Впоследствии левая половина дереваполучает новое разделение между A и
B, которое помещает A на листе с
кодом 00 и B на листе с кодом 01.
◦ После четырех процедур разделения
получается дерево кодов. В конечном
дереве трем символам с
наибольшими частотами присвоены 2разрядные коды, а два символа с
меньшими значениями имеют 3разрядные коды
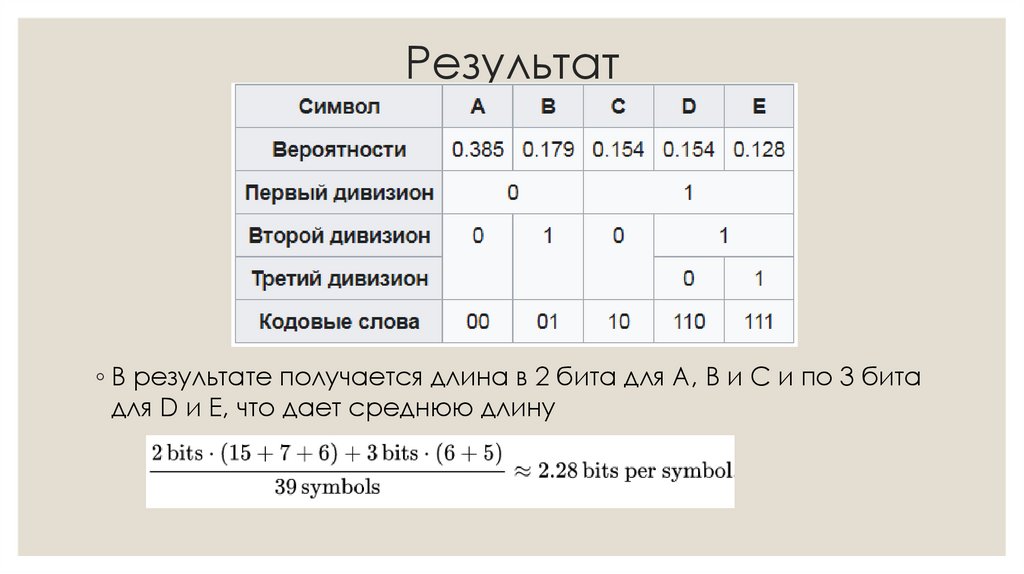
15. Результат
◦ В результате получается длина в 2 бита для A, B и C и по 3 битадля D и E, что дает среднюю длину
16.
17. Составить кодовое дерево
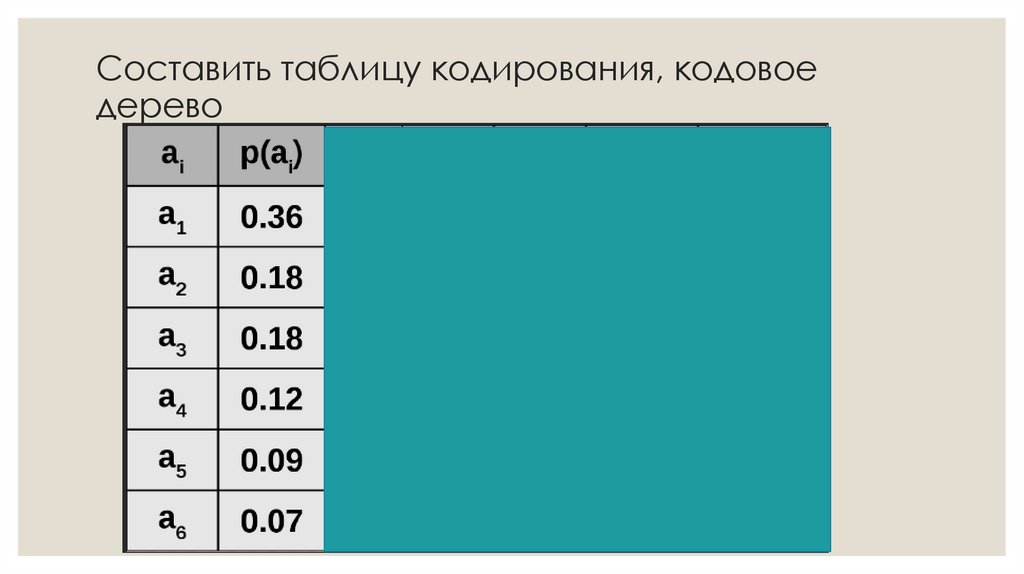
18. Составить таблицу кодирования, кодовое дерево
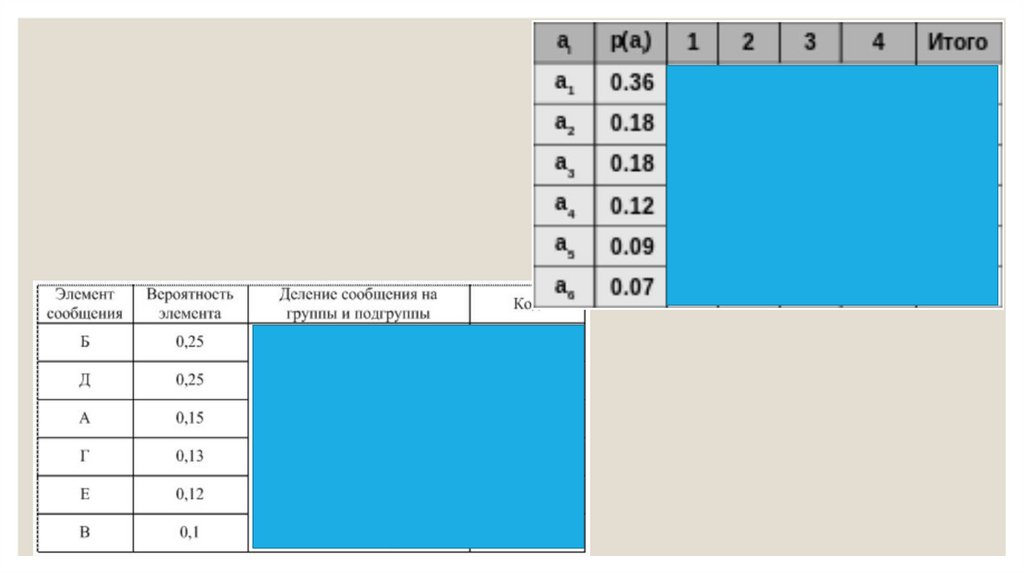
19. Составить таблицу кодирования, кодовое дерево
20.
21.
22.
23. Алгоритм Шеннона-Фано
◦ Дана последовательность символов: AAABCCCCDEEEFG◦ p(A) = 3/14, p(B) = 1/14, p(C) = 4/14, p(D) = 1/14 p(E) = 3/14, p(F) = 1/14, p(G) = 1/14
Отсортируем таблицу в порядке убывания вероятности символов:
Символ
Вероятность
Символ
Вероятность
С
4/14
A
3/14
E
3/14
B
1/14
D
1/14
F
1/14
G
1/14
24. Алгоритм Шеннона-Фано
◦ Построим кодовое дерево от корня к листьям (сверху вниз)25.
◦ Левому символу (с большей вероятностью) присвоим значение 1, правому – 0.26.
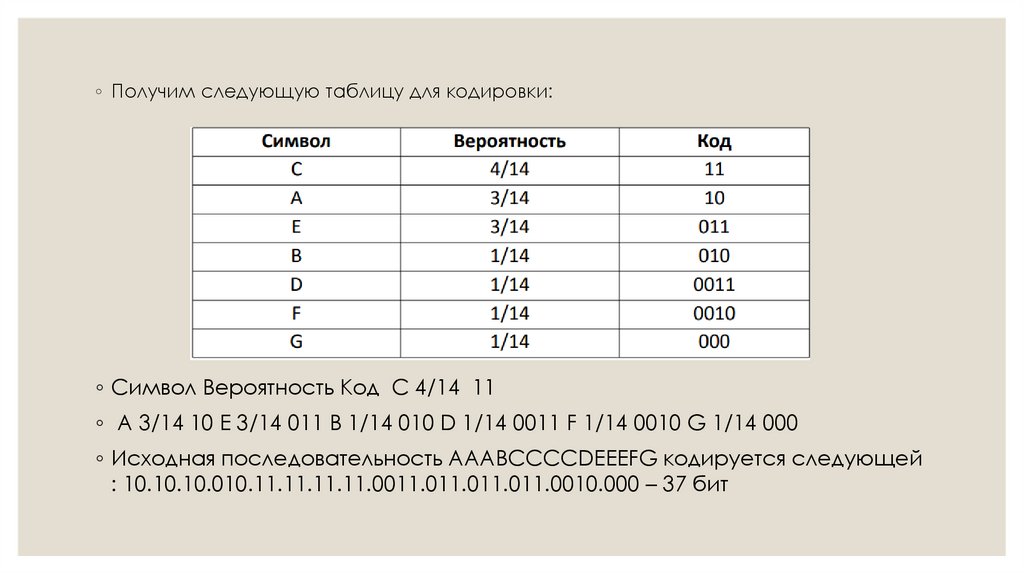
◦ Получим следующую таблицу для кодировки:◦ Символ Вероятность Код С 4/14 11
◦ A 3/14 10 E 3/14 011 B 1/14 010 D 1/14 0011 F 1/14 0010 G 1/14 000
◦ Исходная последовательность AAABCCCCDEEEFG кодируется следующей
: 10.10.10.010.11.11.11.11.0011.011.011.011.0010.000 – 37 бит
27. Алгоритм (код) Хаффмана
АЛГОРИТМ (КОД)ХАФФМАНА
28. Алгоритм (код) Хаффмана
◦ Код Хаффмана Сжатие данных поХаффману применяется при сжатии фото- и
видеоизображений (JPEG, стандарты сжатия
MPEG), в архиваторах (PKZIP, LZH), в протоколах
передачи данных MNP5 и MNP7.
Дэвид Хаффман
(1925-1999) – аспирант
Фано
29.
◦ Кодовое дерево (дерево кодирования Хаффмана, Ндерево) – это бинарное дерево, у которого:◦ листья помечены символами, для которых разрабатывается
кодировка;
◦ узлы (в том числе корень) помечены суммой вероятностей
появления всех символов, соответствующих
листьям поддерева, корнем которого является
соответствующий узел.
◦ Метод Хаффмана на входе получает таблицу частот
встречаемости символов в исходном тексте. Далее на
основании этой таблицы строится дерево кодирования
Хаффмана.
30. Построение дерева по методу Хаффмана
1. Символы входного алфавита образуют список свободных узлов. Каждый узелимеет вес, равный вероятности появления символа в сжимаемом тексте.
2. Выбираются два свободных узла дерева с наименьшими весами.
3. Создается их родитель с весом, равным их суммарному весу. После этого шага
родитель рассматривается как свободный узел.
4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из
этого списка.
5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой – бит 0
(для определённости можно считать, что к узлу с бóльшим весом соответствует 1,
с меньшим – 0).
6. Повторяем шаги 2-6, пока в списке свободных узлов не останется только один
свободный узел. Он и будет считаться корнем дерева.
31. Пример построения дерева по методу Хаффмана
◦ Сжимаемое сообщение – AAABCCCCDEEEFG (то же, что при использованииалгоритма Шеннона-Фано). Соответственно: p(A) = 3/14, p(B) = 1/14, p(C) = 4/14,
p(D) = 1/14, p(E) = 3/14, p(F) = 1/14, p(G) = 1/14.
◦ Построим кодовое дерево (снизу вверх)
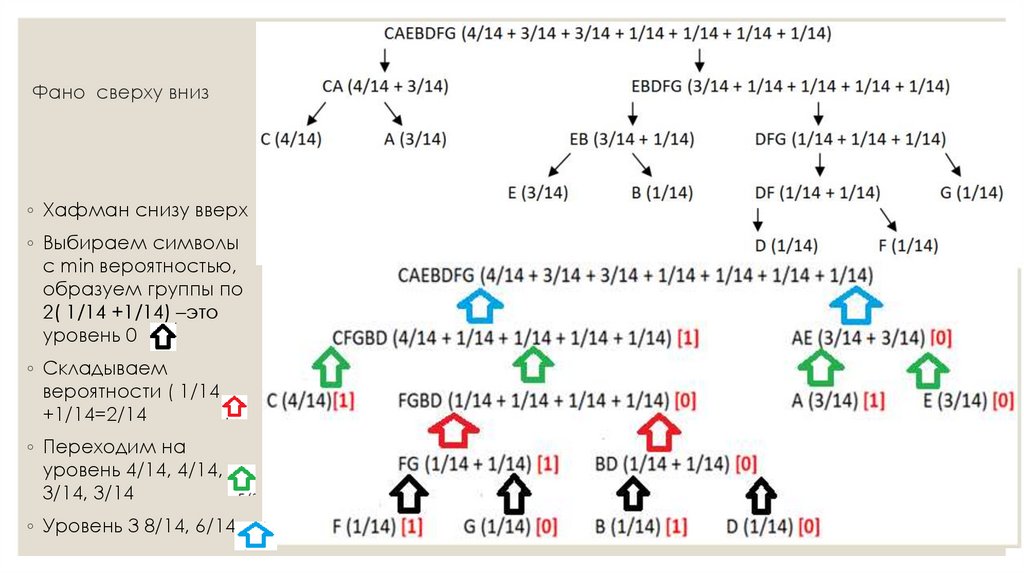
32. Фано сверху вниз
◦ Хафман снизу вверх◦ Выбираем символы
с min вероятностью,
образуем группы по
2( 1/14 +1/14) –это
уровень 0
◦ Складываем
вероятности ( 1/14
+1/14=2/14
◦ Переходим на
уровень 4/14, 4/14,
3/14, 3/14
◦ Уровень 3 8/14, 6/14
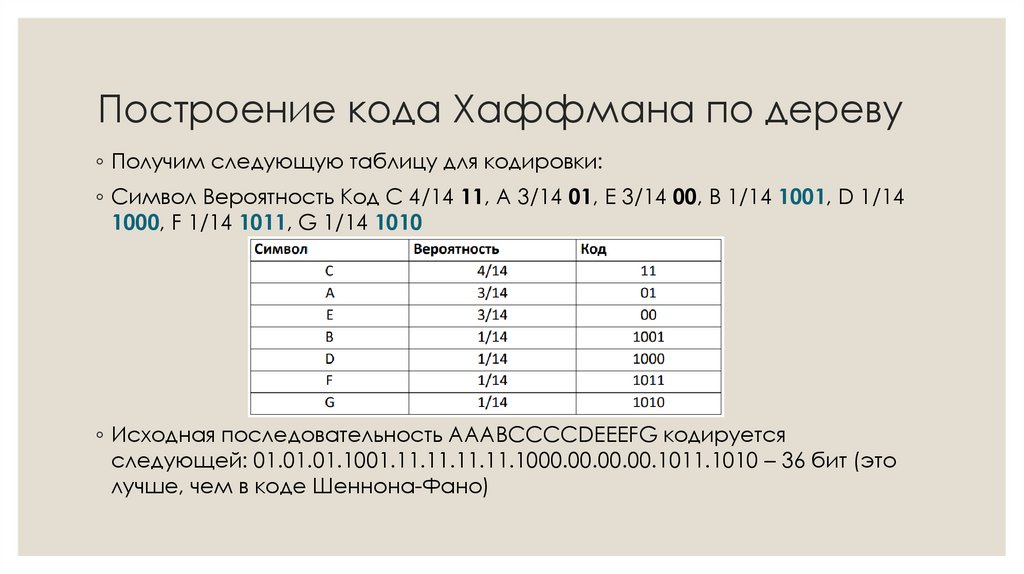
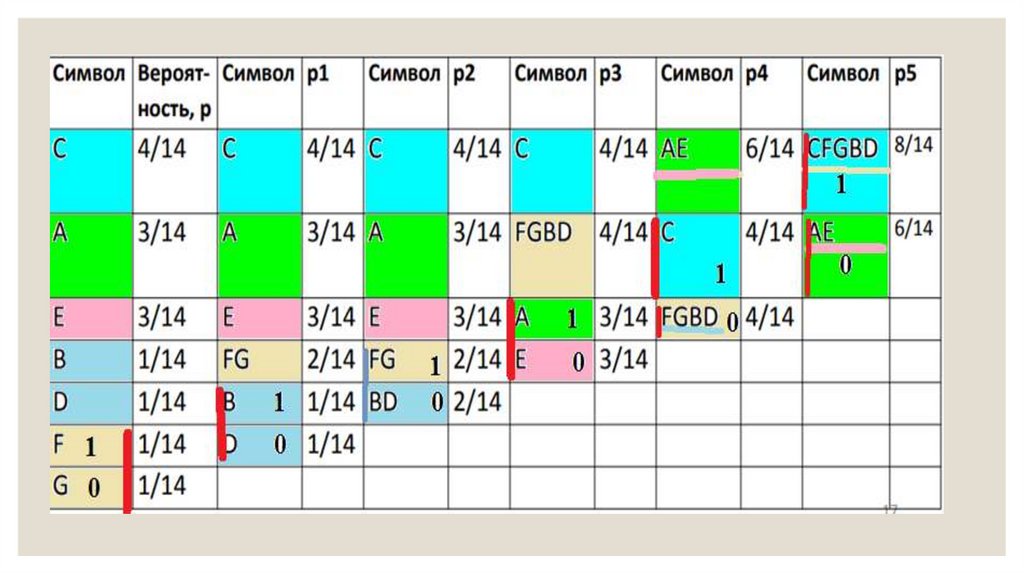
33. Построение кода Хаффмана по дереву
◦ Получим следующую таблицу для кодировки:◦ Символ Вероятность Код С 4/14 11, A 3/14 01, E 3/14 00, B 1/14 1001, D 1/14
1000, F 1/14 1011, G 1/14 1010
◦ Исходная последовательность AAABCCCCDEEEFG кодируется
следующей: 01.01.01.1001.11.11.11.11.1000.00.00.00.1011.1010 – 36 бит (это
лучше, чем в коде Шеннона-Фано)
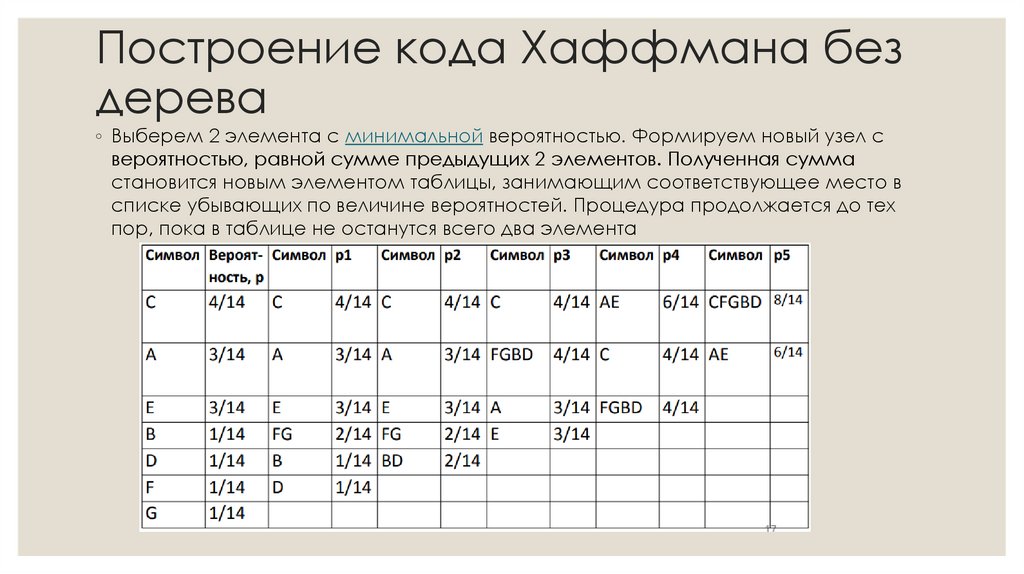
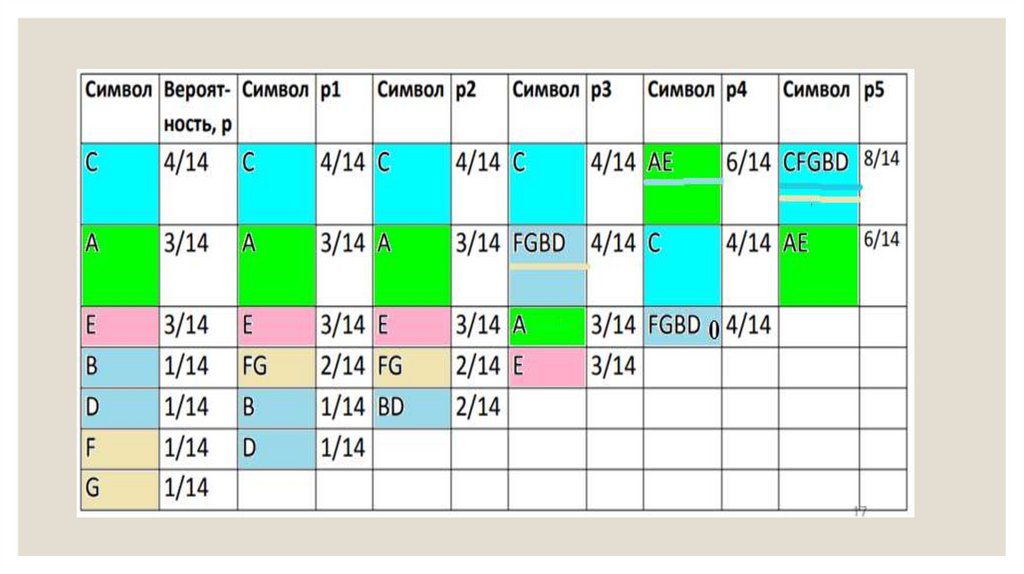
34. Построение кода Хаффмана без дерева
◦ Выберем 2 элемента с минимальной вероятностью. Формируем новый узел свероятностью, равной сумме предыдущих 2 элементов. Полученная сумма
становится новым элементом таблицы, занимающим соответствующее место в
списке убывающих по величине вероятностей. Процедура продолжается до тех
пор, пока в таблице не останутся всего два элемента
35.
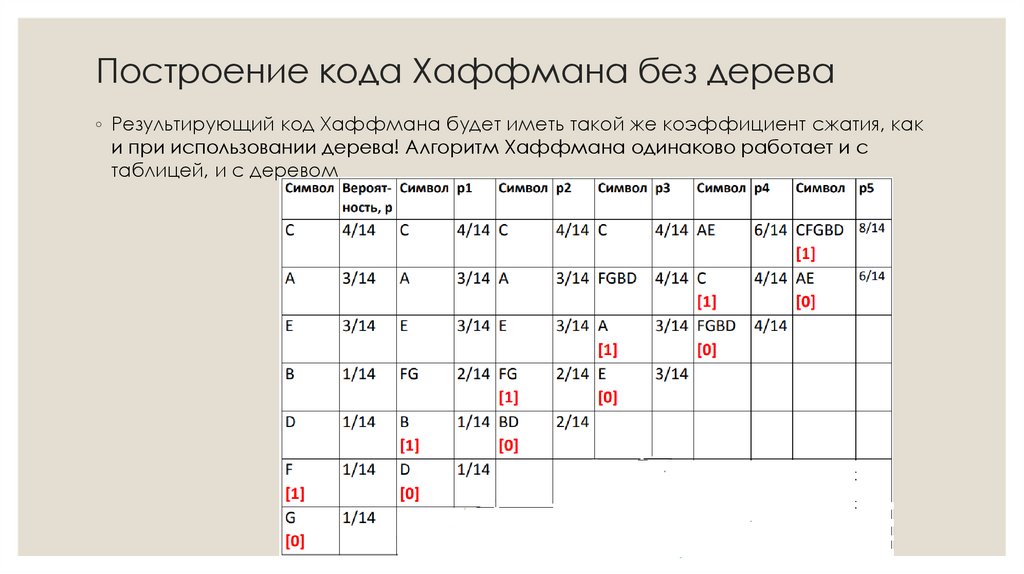
36. Построение кода Хаффмана без дерева
◦ Результирующий код Хаффмана будет иметь такой же коэффициент сжатия, каки при использовании дерева! Алгоритм Хаффмана одинаково работает и с
таблицей, и с деревом
37.
38. Задание
◦ Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г,решили использовать неравномерный по длине код: A=0, Б=10, В=110. Как нужно
закодировать букву Г, чтобы длина кода была минимальной и допускалось
однозначное разбиение кодированного сообщения на буквы?1) 1 2) 1110 3) 111 4) 11
◦ Для 5 букв латинского алфавита заданы их двоичные коды. Эти коды представлены в
таблице:
Определить, какой набор букв закодирован двоичной
◦
строкой
0110100011000
◦ Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г,
решили использовать неравномерный по длине код: A=0, Б=10, В=110. Как нужно
закодировать букву Г, чтобы длина кода была минимальной и допускалось
однозначное разбиение кодированного сообщения на буквы?
39. Задание
◦ Составить таблицу кодов символов для фразыНА_ДВОРЕ_ТРАВА,_НА_ТРАВЕ_ДРОВА
40.
41.
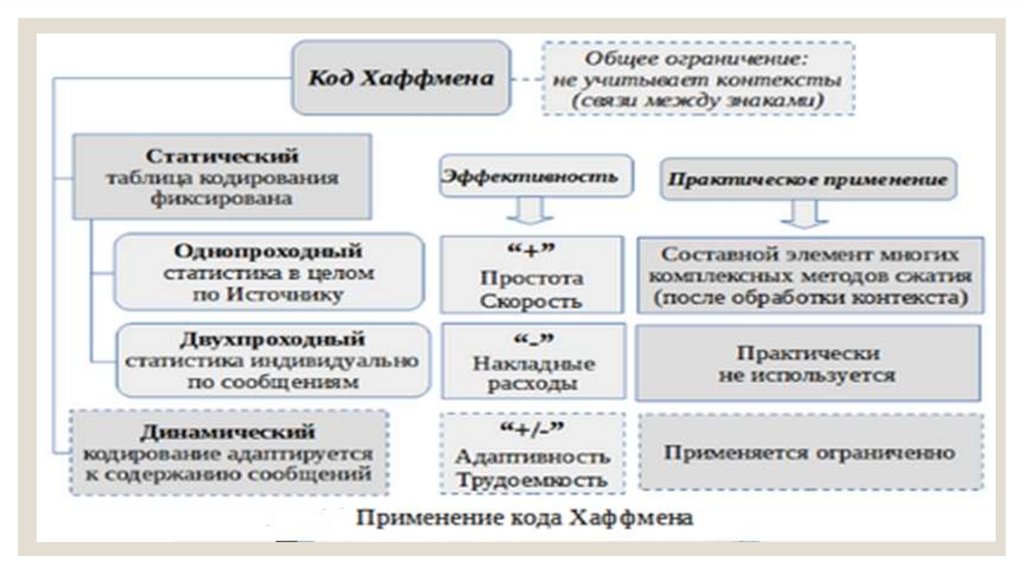
◦ рассмотренный выше способ кодирования относится кклассу статических. Здесь оценки вероятностей и
таблица соответствия знаков и кодов остаются
неизменными. При этом они могут опираться на
обобщенную статистику Источника или на
индивидуальную статистику конкретных сообщений. Во
втором случае для каждого сообщения первоначально
должны быть подсчитаны вероятности появления знаков,
а уже затем на основе этих данных выполнено
кодирование. Соответственно, такой способ называют
двухпроходным в отличие от первого - однопроходного;
42.
◦ однопроходный способ получил наибольшеераспространение. Он применяется в основном как
составная часть комплексных алгоритмов сжатия. Это
компенсирует важный общий недостаток
статистического кодирования — отсутствие учета
контента. Поскольку в рамках комплексных методов
этот алгоритм работает с уже преобразованными
данными, ослабляется их зависимость от конкретного
содержания сообщений. С другой стороны простота и
высокая скорость кодирования составляют важное
достоинство метода;
43.
◦ двухпроходный способ не нашел практического примененияв силу одного важного недостатка: здесь таблица
кодирования индивидуальна для каждого сообщения и ее
необходимо передавать от кодера к декодеру.
Соотвествующие накладные расходы нивелируют
достоинства более точного учета статистики. Кроме того
очевидны потери в скорости;
◦ динамический способ максимально адаптивен, поскольку
код здесь формируется прямо по ходу обработки
сообщения. Однако, такой подход трудоемок, а главное, не
снимает главной проблемы — отсутствия учета контента. На
практике он применяется ограниченно.































 informatics
informatics








