Тема 4.1 Криптографические хеш-функции (1)

1.

1
Тема 4.1
Криптографические
хеш-функции

2.

Содержание
1. Функции хеширования и целостность данных
2. Типы криптографических хеш-функций
3. Алгоритмы хеш-функций
2

3.

3
1. Функции хеширования и
целостность данных

4.

Применение хеш-функций
4
при проведении статистических экспериментов:
наблюдаемые случайные величины с бесконечным числом исходов
удобнее заменять на случайные величины с конечным числом
исходов;
тестировании логических устройств:
для тестирования микросхем на их вход подают очень длинную
тестовую последовательность,
а затем значение хеш-функции от выходной последовательности
сравнивают с эталонным;
построении алгоритмов быстрого поиска в текстовых БД:
для осуществления поиска нужного сообщения в большом списке
сообщений различной длины удобнее сравнивать друг с другом не
сами сообщения,
а короткие значения их сверток, играющих одновременно роль
контрольных сумм;
проверке целостности записей в БД:
при извлечении каждой записи вычисляют значение свертки и
сравнивают с хранимым истинным значением контрольной суммы,
а также во многих других случаях.

5.

Определение хеш-функции
5
Пусть X – множество, элементы которого будем называть
сообщениями.
Обычно полагают X А*, где А* – множество конечных
последовательностей символов из некоторого
конечного алфавита А (как правило, А = {0, 1}).
Пусть Y = Vn – множество двоичных векторов фиксированной
длины n.
Хеш-функцией h называют всякую легко вычисляемую
функцию
h: X Y.

6.

Определение хеш-функции
Основным требованием, предъявляемым к таким хешфункциям, является равномерность распределения их
значений при случайном выборе значений аргументов.
Для конечного множества X при случайном и
равновероятном выборе сообщений это условие
эквивалентно наличию одинакового числа прообразов,
т.е. сообщений с заданным значением хеш-функции,
для каждого значения свертки.
Обычно число возможных сообщений значительно
превосходит число возможных значений сверток. Поэтому
для каждого значения свертки имеется большое число
прообразов.
При этом пару сообщений с одинаковыми значениями
хеш-функции называют коллизией.
6

7.

Определение хеш-функции
Хэш-функция – преобразование битовой строки
произвольной длины в битовую строку (блок)
фиксированной длины (обычно, n=160-512 битов),
обладающее следующими свойствами.
Восстановление по z, исходя из соотношения z=h(m),
вычислительно нереализуемо.
Более того, исходя из заданных m и z, вычислительно
нереализуемо определение второго прообраза для z,
т.е. такого сообщения m1≠m, что z=h(m)=h(m1).
На практике, как правило, используются хэш-функции,
удовлетворяющие более жесткому, чем последнее,
условию:
требуется вычислительная нереализуемость
нахождения произвольной коллизии,
т.е. пары сообщений x, y таких, что h(x)=h(y).
7

8.

Определение хеш-функции
Значение хэш-функции называется хэш-кодом или
дайджестом.
Наиболее часто встречаются хэш-функции, построенные в
виде последовательности итераций, на каждом шаге
которых применяются т.н. одношаговые функции
сжатия.
Эти функции являются вектор-функциями от двух
переменных вида y = f(x1, x2),
где аргументы являются двоичными векторами
размерности m,
а значение функции – вектор размерности n.
Величина n< m является длиной хэш-кода.
8

9.

Определение хеш-функции
9
Для вычисления хэш-кода h(M)
сообщение M дополняется тем или иным образом до
длины кратной m
и разбивается на блоки M1, M2, …, MN.
Затем вычисляется последовательность итераций:
H0=V, где V – фиксированный вектор (т.н. вектор
инициализации);
Нi = f (Мi, Hi-1), i = 1, ..., N ;
в качестве хэш-кода принимается значение h(M)=HN .

10.

Определение хеш-функции
10
Очевидно, при вычислении хэш-функций можно
использовать дополнительный секретный параметр,
скажем K.
Соответствующие процедуры называются
алгоритмами вычисления кодов аутентификации
сообщения.
Встречается также название – ключевая хэш-функция.
В этом случае значение хэш-кода h(M, K)
называется кодом аутенификации сообщения
и имеет общепринятую аббревиатуру МАС.

11.

Целостность данных и аутентификация
сообщений
11
В криптографических приложениях хеш-функции применяют,
прежде всего, для
установления целостности
и аутентификации источника данных.
Рассмотрим эти свойства более подробно.

12.

Целостность данных и аутентификация
сообщений
Термин аутентификация означает установление
подлинности. Он может относиться ко всем аспектам
взаимодействия:
сеансу связи,
взаимодействующим сторонам,
передаваемым сообщениям и т.д.
Применительно к самой информации аутентификация
означает проверку того, что данные, передаваемые по
каналу связи, являются подлинными
по своему источнику и содержанию,
по времени создания,
времени пересылки и т.д.
12

13.

Целостность данных и аутентификация
сообщений
13
Целостность данных – свойство, позволяющее убедиться
в том, что данные не изменялись неавторизованным
способом с тех пор, как они были
созданы,
переданы
или сохранены авторизованным источником.
Под изменениями обычно понимают
пропуски,
вставки,
замены
и перестановки фрагментов сообщения.

14.

Целостность данных и аутентификация
сообщений
14
Аутентификация источника данных – получение
подтверждения того, что рассматриваемый документ был
создан именно указанным источником информации.
При этом не требуется проверка времени создания и
единственности документа,
важно только то, что он был создан в некоторый (обычно
неопределенный) момент времени в прошлом.
Нарушение «единственности документа», в частности,
подразумевает его повторную передачу или повторное
использование.
Если источник сообщений фиксирован, то вместо термина
«аутентификация источника данных» используют термин
«аутентификация сообщений».

15.

Целостность данных и аутентификация
сообщений
15
Целостность данных и аутентификация источника данных
тесно связаны друг с другом.
Действительно, если данные подверглись модификации,
то у них автоматически изменился источник.
Если же не установлен источник, то без ссылки на него
нельзя разрешить проблему целостности.
В связи с этим обычно полагают, по определению, что
аутентификация источника данных включает проверку
целостности данных.

16.

Целостность данных и аутентификация
сообщений
16
Особо остановимся на дополнительном гарантировании
единственности и своевременности передачи сообщений.
В этом случае используют термин «аутентификация
транзакции», означающий аутентификацию сообщения
с подтверждением единственности и своевременности
передачи данных.
Такой тип аутентификации предоставляет возможность
защиты от повторного использования ранее переданных
сообщений.
Это является необходимым в тех случаях, когда подобная
угроза может привести к нежелательным последствиям.
Примером таких приложений являются электронные банковские
платежи или системы автоматизированного управления
подвижными объектами.

17.

Целостность данных и аутентификация
сообщений
17
Для обеспечения единственности и своевременности
передачи сообщений обычно используют дополнительные
параметры, которые добавляют к передаваемым
сообщениям.
Это могут быть метки времени или некоторые
последовательности чисел.
Если метки времени позволяют установить время
создания или передачи документа,
то последовательность чисел гарантирует
правильность порядка получения сообщений.

18.

18
2. Типы криптографических хешфункций

19.

Типы криптографических хеш-функций
19
В криптографии особо выделяют два важных типа
криптографических хеш-функций:
задаваемые ключом
и не зависящие от ключа (или бесключевые), часто
называемые просто хеш-функциями.
Рассмотрим их применение для решения задач контроля
целостности данных и аутентификации источника данных.

20.

Типы криптографических хеш-функций
Хеш-функции, задаваемые ключом, применяют в
системах с симметричными ключами и доверяющими
друг другу сторонами.
Если передающая и проверяющая стороны доверяют
друг другу,
то они могут иметь общий секретный ключ.
20

21.

Типы криптографических хеш-функций
При решении задачи контроля целостности для каждого
набора данных вычисляют значение хеш-функции,
называемое кодом аутентичности сообщения,
которое передают или хранят вместе с самими данными.
При получении данных пользователь
вычисляет значение свертки
и сравнивает его с имеющимся контрольным
значением.
Несовпадение говорит о том, что данные были
изменены.
21

22.

Типы криптографических хеш-функций
22
Хеш-функция, служащая для выработки кода
аутентичности сообщения, должна позволять (в отличие
от обычной контрольной суммы)
обнаруживать не только случайные ошибки в наборах
данных, возникающие при их хранении и передаче,
но и сигнализировать об активных атаках
злоумышленника, пытающегося осуществить
навязывание ложной информации.
Для того чтобы злоумышленник
не мог самостоятельно вычислить контрольное
значение свертки
и тем самым осуществить успешную имитацию или
подмену данных,
хеш-функция должна существенно зависеть от
секретного, не известного злоумышленнику ключа
пользователя.

23.

Типы криптографических хеш-функций
Применение зависящих от ключа хеш-функций не
позволяет противнику
создавать поддельные, сфабрикованные сообщения
при атаках типа имитация
и модифицировать передаваемые сообщения при
атаках типа подмена.
Аутентификация источника при этом выполняется
автоматически,
т.к. никто кроме двух сторон, обладающих общим
секретным ключом, не может вычислить
правильное значение хеш-функции.
23

24.

Типы криптографических хеш-функций
24
Хеш-функции, задаваемые ключом, называют кодами
аутентификации сообщений (message authentication
code – MAC). Они дают возможность без дополнительных
средств гарантировать
как подлинность источника данных,
так и целостность данных в системах с доверяющими
друг другу пользователями.

25.

Типы криптографических хеш-функций
В случае с не доверяющими друг другу сторонами
ключ должен быть известен только одной передающей
стороне,
а проверяющая сторона должна пользоваться только
открытой информацией.
В связи с этим использование симметричных систем
уже не представляется возможным.
25

26.

Типы криптографических хеш-функций
В такой ситуации применяют схемы цифровой подписи,
позволяющие осуществлять
контроль целостности
и аутентификацию источника данных.
Как правило, при этом сообщение, прежде чем быть
удостоверенным личной подписью, зависящей от
секретного ключа пользователя,
«сжимается» с помощью хеш-функции, выполняющей
функцию кода обнаружения ошибок.
26

27.

Типы криптографических хеш-функций
27
В данном случае хеш-функция не зависит от секретного
ключа и может быть известна всем.
Основными требованиями к ней являются
однонаправленность, дающая гарантии невозможности
подделки,
т.е. подбора сообщения с правильным значением
подписи,
а также трудность нахождения коллизий,
гарантирующая невозможность подмены
подписанного документа.

28.

Одношаговые сжимающие функции
28
Как правило, хеш-функции строят на основе так называемых
одношаговых сжимающих функций y = f(x1, x2),
зависящих от двух переменных,
где x1, x2, y – двоичные векторы длиной т и n
соответственно,
причем n – длина свертки.

29.

Одношаговые сжимающие функции
29
Для получения значения h(M)
сообщение М сначала разбивают на блоки длиной т,
при этом если длина сообщения не кратна т, то
последний блок неким специальным образом
дополняют до полного,
а затем к полученным блокам М1, М2, ..., МN
применяют следующую последовательную процедуру
вычисления свертки:
Н0 = V,
Нi = f (Мi, Hi-1), i = 1, ..., N.
h(M) = HN.
(1)

30.

Одношаговые сжимающие функции
В формуле V – некоторый фиксированный начальный
вектор.
Если функция f задается ключом,
то этот вектор можно принять равным нулевому
вектору.
Если же функция f не зависит от ключа,
то для исключения возможности перебора коротких
сообщений (при попытках обращения хеш-функции)
этот вектор можно составить из фрагментов,
указывающих
дату,
время,
номер сообщения и т. п.
30

31.

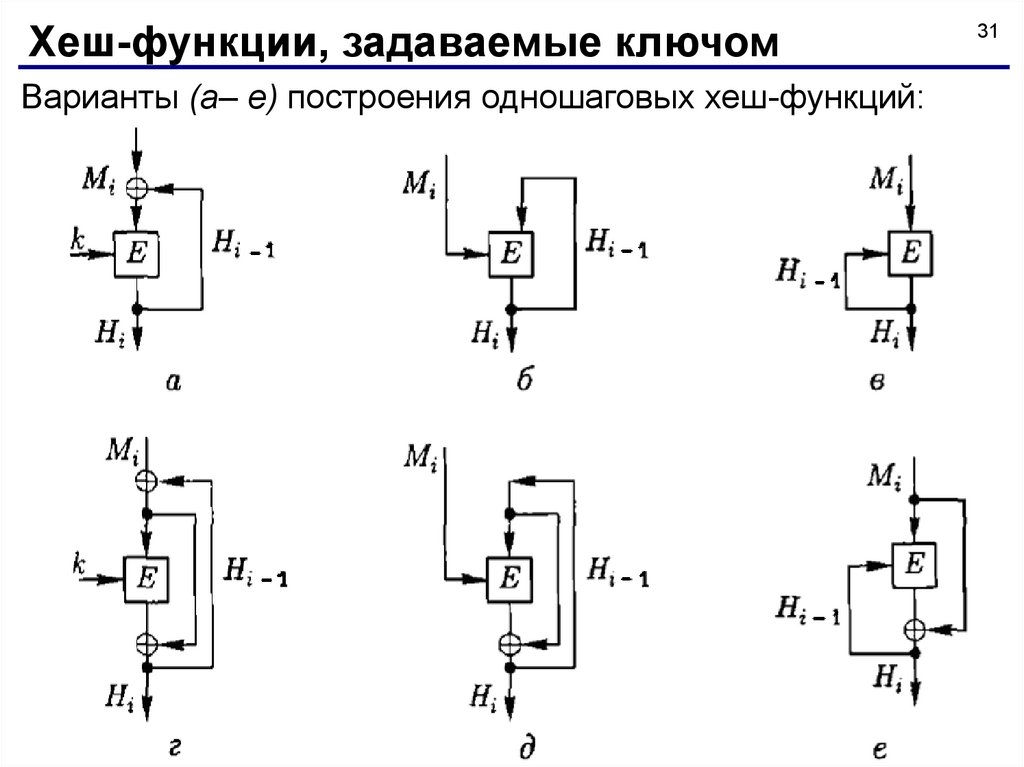
Хеш-функции, задаваемые ключом
Варианты (a– e) построения одношаговых хеш-функций:
31

32.

Хеш-функции, задаваемые ключом
32
Ключевые функции применяют в ситуациях, когда стороны
доверяют друг другу и могут иметь общий секретный ключ.
Обычно в этих условиях не требуется, чтобы система
обеспечивала защиту в случае отказа получателя от
факта получения сообщения или его подмены.
Поэтому от хеш-функций, задаваемых ключом, не
требуется устойчивости к коллизиям.

33.

Хеш-функции, не зависящие от ключа
33
Обычно требуется, чтобы хеш-функции, не зависящие от
ключа, обладали следующими свойствами:
однонаправленность;
устойчивость к коллизиям;
устойчивость к нахождению второго прообраза.
Эти свойства означают, соответственно высокую сложность
нахождения
сообщения с заданным значением свертки,
пары сообщений с одинаковыми значениями свертки,
второго сообщения с тем же значением свертки для
заданного сообщения с известным значением свертки.
Например, хеш-функция CRC-32, представляющая контрольную сумму,
является линейным отображением и поэтому не удовлетворяет ни
одному из этих трех свойств.

34.

Хеш-функции, не зависящие от ключа
34
Замечание.
Трудоемкость подбора прообраза для
однонаправленной функции или трудоемкость поиска
второго прообраза оценивают величиной O(2n).
В то же время трудоемкость поиска коллизии
оценивают величиной O(2n/2),
т.к. в данной ситуации применима атака, основанная
на парадоксе дней рождений.
Парадокс дней рождений заключается в том, что
вероятность р наличия коллизии (т.е. совпадения) в
выборке из m элементов объема O m принимает
достаточно большое значение.

35.

35
3. Алгоритмы хеш-функций

36.

Примеры бесключевых хеш-функций
36
Примеры бесключевых хеш-функций дают известные
алгоритмы:
MD4 (Message Digest),
MD5,
RIPEMD–160
предложен организацией RIPE
и SHA-1
предложен Агентством национальной безопасности
США и введен в действие Национальным
институтом стандартов (NIST) США в качестве
стандарта SHS (Secure Hash Standard) в 1995г..
Они оперируют с блоками длиной n, совпадающей с длиной
результирующего значения свертки, причем
n=128 для алгоритмов MD4, MD5,
n=160 для алгоритмов RIPEMD–160 и SHA-1.

37.

Примеры бесключевых хеш-функций
37
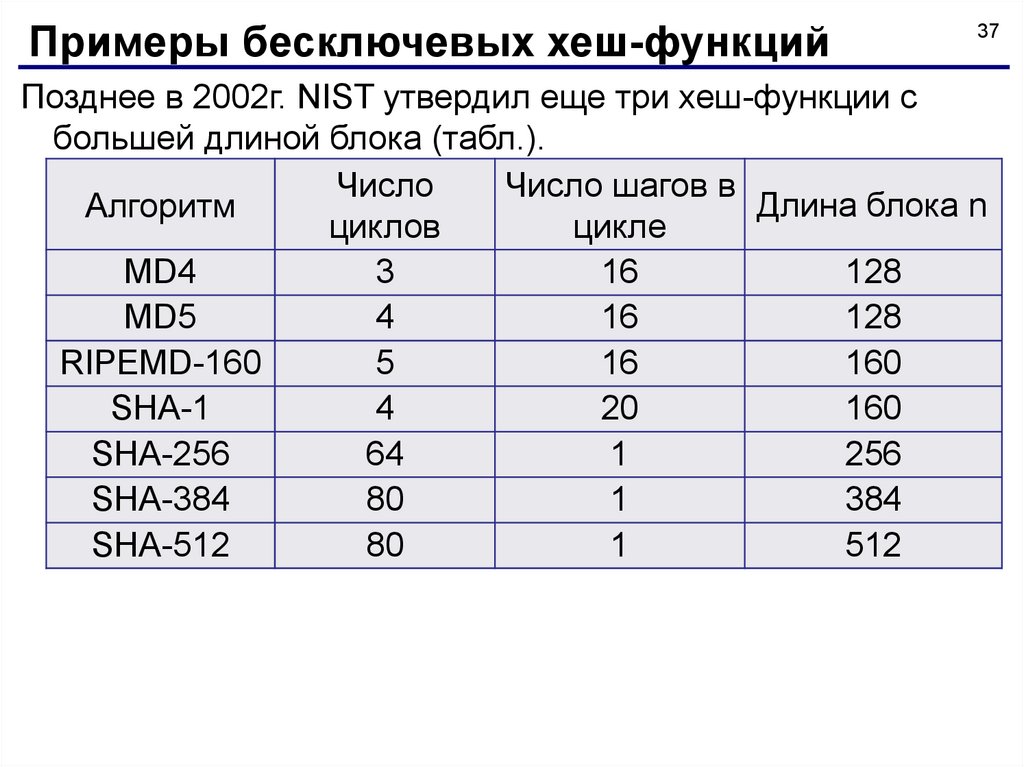
Позднее в 2002г. NIST утвердил еще три хеш-функции с
большей длиной блока (табл.).
Число
Число шагов в
Длина блока n
Алгоритм
циклов
цикле
MD4
3
16
128
MD5
4
16
128
RIPEMD-160
5
16
160
SHA-1
4
20
160
SHA-256
64
1
256
SHA-384
80
1
384
SHA-512
80
1
512

38.

Алгоритмы хеш-функций
38
Указанные алгоритмы спроектированы специально с учетом
эффективной реализации на современных ЭВМ.
При их использовании исходное сообщение М
разбивают на блоки Мi длиной т = 512 бит.
В результате получают последовательность блоков
M1, М2, …, MN.
Последний блок формируют
путем дописывания к концу сообщения комбинации
10... 0 до получения блока размером 448 бит,
к которому затем добавляют комбинацию из 64 бит,
представляющую битовую длину сообщения.

39.

Алгоритмы хеш-функций
39
Затем вычисляют значение свертки согласно процедуре
(1, слайд 29) с использованием одношаговой
сжимающей функции
f(x, H) = Еx(Н) Н
по правилу
Нi = f(Mi, Hi–1), 1 i N,
где Mi – блок сообщения длиной т бит;
Нi – блоки из n бит;
Еx – некоторое преобразование множества блоков;
значение начального вектора Н0 определяется в
описании алгоритма Ех.

40.

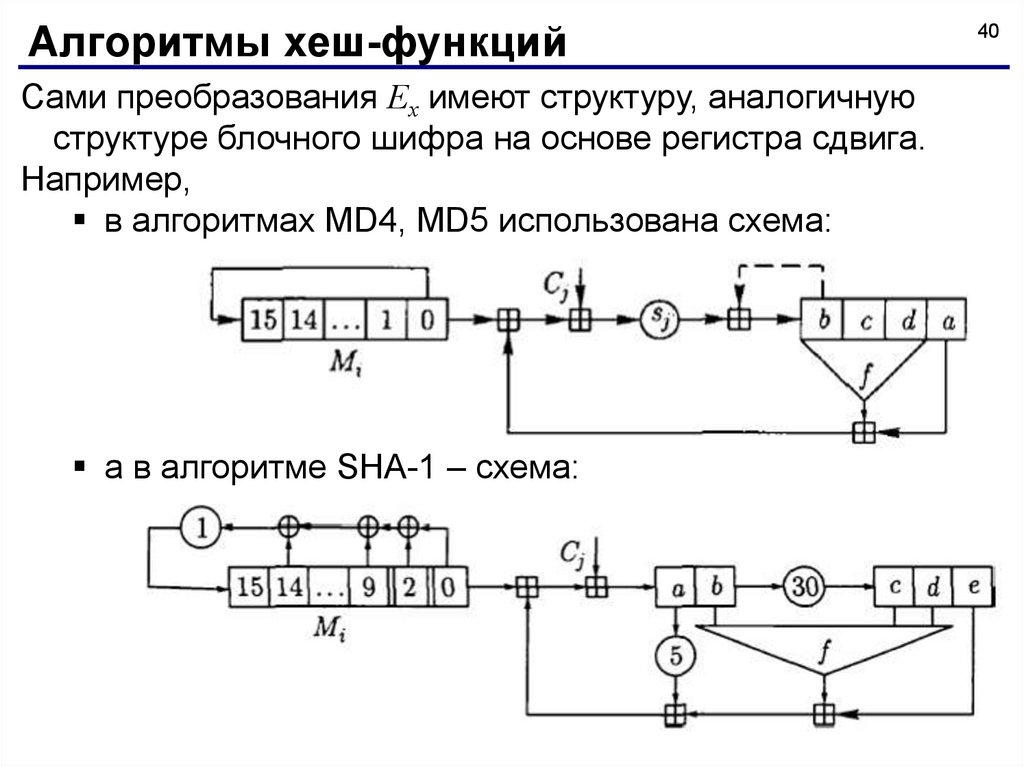
Алгоритмы хеш-функций
Сами преобразования Ех имеют структуру, аналогичную
структуре блочного шифра на основе регистра сдвига.
Например,
в алгоритмах MD4, MD5 использована схема:
а в алгоритме SHA-1 – схема:
40

41.

Алгоритмы хеш-функций
41
Блок открытого текста длиной 512 бит записывается в
накопитель, который работает как циклический регистр
сдвига длиной 14 с размером ячейки 32 бита.
В каждом такте с него считывается 32 бита и подается на
вход нелинейного регистра
длиной 4 для MD
и длиной 5 для SHA.
Начальный вектор H0 = (a, b, c, d) записывается во второй
регистр в указанном на рис. слайда 40 порядке.
Заключительное состояние, в которое перейдет второй
регистр после выполнения всех циклов, будет определять
искомое значение свертки HN=(а', b', c', d').
Для усложнения на каждом шаге j
происходит суммирование с некоторыми заранее
заданными константами Cj,
а также выполняются определенные циклические сдвиги sj.
Функции fj(b, c, d) меняются определенным образом.

42.

Алгоритмы хеш-функций
В алгоритме MD4 выполняется 3 цикла по 16 шагов, в
которых применяются соответственно функции:
(b c) ( b d)
(b c) (b d) (c d)
b c d
где символами , , обозначены логические функции
покоординатных соответственно
дизъюнкции, конъюнкции и отрицания двоичных
векторов.
42

43.

Алгоритмы хеш-функций
43
В алгоритме MD5 выполняется 4 цикла по 16 шагов, в
которых применяются соответственно функции:
(b c) ( b d)
(b c) (b d) (c d)
b c d
b (c d)
Кроме того, в алгоритме MD5 введена дополнительная
обратная связь, показанная на рис. слайда 40 пунктиром.

44.

Стандарты хеш-функций
44
В алгоритме SHA-1 выполняется 4 цикла по 20 шагов, в
которых применяются соответственно функции:
(b d) (c d)
b c d
(b c) (b d) (c d)
b c d
При этом по сравнению с алгоритмом MD4 изменен
как первый регистр, в котором введена линейная
обратная связь,
так и второй, длина которого увеличена до 5 ячеек (рис.
слайда 40).
Значения циклических сдвигов в этом алгоритме
фиксированы.

45.

Стандарты хеш-функций
45
В стандарте хеш-функции ГОСТ Р 34.11-94 приняты
значения n = m = 512.
Одношаговая сжимающая функция f(x, H), используемая
для вычисления последовательности значений
Hi = f(Mi, Hi–1),
построена на базе 4 параллельно работающих схем
блочного шифрования (ГОСТ 28147-89), каждая из
которых
имеет 256-битовый ключ
и оперирует с блоками размером 64 бита.
Каждый из ключей вычисляют в соответствии с
некоторой линейной функцией от блока исходного
сообщения хi и значения Hi–1.

46.

Стандарты хеш-функций
46
Значение Hi является линейной функцией результата
шифрования, блока исходного сообщения Mi и значения
Hi–1.
После вычисления значения HN для
последовательности блоков М1, М2,…, MN применяют
еще два шага вычисления согласно формуле
Н = h(M) = f( , f(L, HN)),
где – сумма по модулю 2 всех блоков сообщения;
L – длина сообщения.

47.

Хеш-функция СТБ 1176.1–99
Государственный стандарт РБ СТБ 1176.1
«Информационная технология. Защита информации.
Функция хеширования» введен в действие 30.09.1999г.
Определяемая стандартом функция h действует на
последовательности байтов.
Хеш-значение является словом длиной L из диапазона
142 L 256.
Используется 256-битовое начальное хеш-значение,
которое выбирается произвольным образом, единым для
группы пользователей.
47

48.

Хеш-функция СТБ 1176.1–99
48
Обозначения.
Преобразования стандарта выполняются над числами
множества
Z(n)={0, 1, …, 2n–1}.
Отождествим число a Z(n) c вектором Vn, содержащим
двоичную запись a, и перенесем на Z(n) действие
операций:
– сложения по модулю 2,
[+] – сложения в Vn по правилу: c =a [+] b,
если c a b mod 2n ,
где v – число 2n–1v1+2n–2v2+…+ vn для вектора v=(v1,
v2, …, vn) Vn,
<<< – циклического сдвига компонентов вектора Vn
(первый аргумент) на указанное число позиций (второй
аргумент).

49.

Хеш-функция СТБ 1176.1–99
Разложение числа a по основанию 2m , ai Z(m), будем
записывать в виде a=ak–1||…||a1||a0.
49

50.

Хеш-функция СТБ 1176.1–99
50
Преобразования.
При вычислении значений h используются следующие
вспомогательные преобразования.
1. Преобразования 0, 1, 2, 3: Z(512) Z(512) действуют
на число X=x15||…||x1||x0, xi Z(32), по правилам:
0(X)=(( x15 x13 x3 x0) [+] C0 ) ||x15||…||x1;
1(X)=(( x15 x2 x0) [+] C1 ) ||x15||…||x1;
2(X)=(( x9 x4 x0) [+] C2 ) ||x15||…||x1;
3(X)=(( x13 x8 x0) [+] C3 ) ||x15||…||x1;
где C0 = (2BDA732E)16, C1 = (3920FE85)16, C2 = (BC1641F9)16,
C3 = (75FE243B)16.

51.

Хеш-функция СТБ 1176.1–99
51
2. В стандарте используются S-блоки s: Z(8) Z(8), j sj,
которые задаются числами s255||…||s1||s0 Z(2048)
Преобразование числа X Z(128) определяют восемь
S-блоков, заданных числами Y1, …, Y8.
Образ (X; Y1, …, Y8) является результатом 32-кратного
действия подстановки Фейстеля:
X X0 ||( X1 f(X0)), X= X1 || X0,
Xi Z(64)
Используемая тактовая функция f : Z(64) Z(64)
действует по правилу:
x8||…||x1 ( s8(x8) ||…|| s1(x1) ) <<< 3, xi Z(8),
где si – S-блок Z(8) Z(8), определяемый числом Yi.

52.

Хеш-функция СТБ 1176.1–99
52
3. Преобразование : Z(256) Z(256) ставит в соответствие
числу X=x7||…||x1||x0, xi Z(32),
число (X)= x6||…||x0|| (x0 x2 x4 x7).
4. Отображение : Z(128) Z(256) Z(256) ставит в
соответствие
числам X=x3||…||x0 и Y=y7||…||y0, xi, yi Z(32),
число (X, Y)= y3||…||y0|| (( y3 [+] x3) y7) ||…|| (( y0 [+] x0) y4).

53.

Хеш-функция СТБ 1176.1–99
Входные данные.
Подлежащее хешированию сообщение M является
последовательностью байтов m1, …, ml Z(8).
Сообщение дополняется таким минимальным числом k
нулевых байтов ml+1, …, ml+k, что n=(l+k)/32 – целое
число.
Затем определяются числа
Mi= m32i ||…|| m32(i–1)+2 || m32(i–1)+1, i=1, …, n,
и число Mn+1= l.
53

54.

Хеш-функция СТБ 1176.1–99
54
Переменные.
При вычислении хеш-значений используются следующие
переменные.
Переменная H Z(256), H = H1 || H0 = h7||…||h0,
где H0, H1 Z(128), hi Z(32).
При выполнении алгоритма переменная H содержит
текущее хеш-значение,
а в начале вычислений – стартовое хеш-значение.
Переменные T0, T1, …, T7 Z(2048).
Значения переменных T1, T3, T5, T7 не изменяются
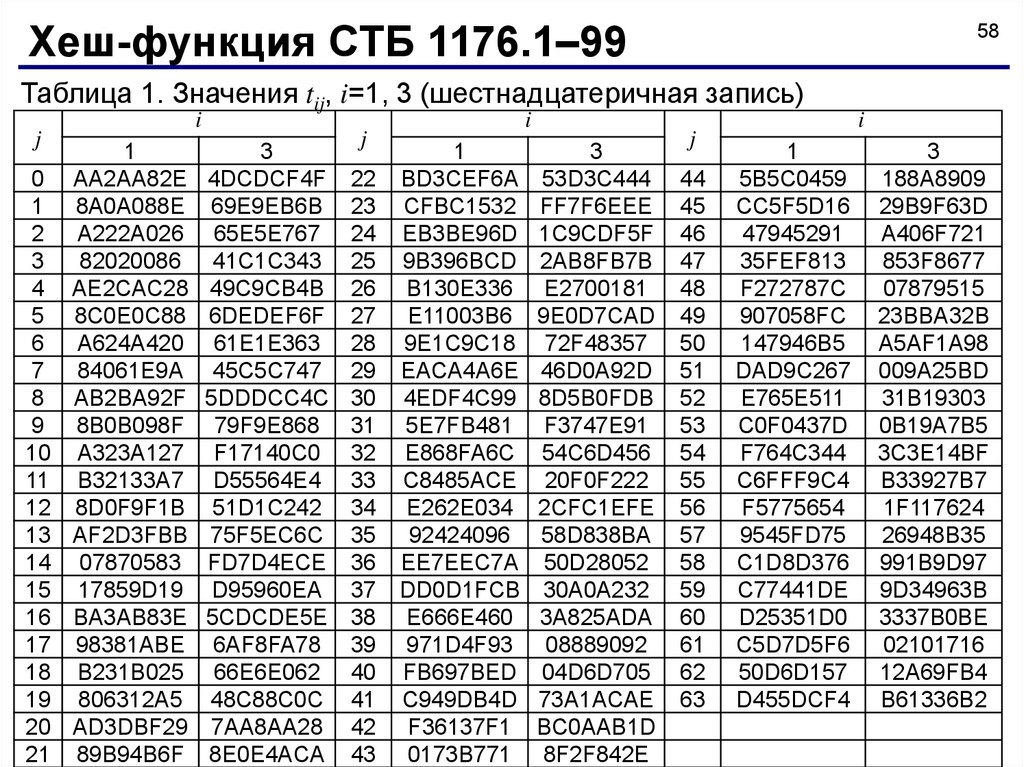
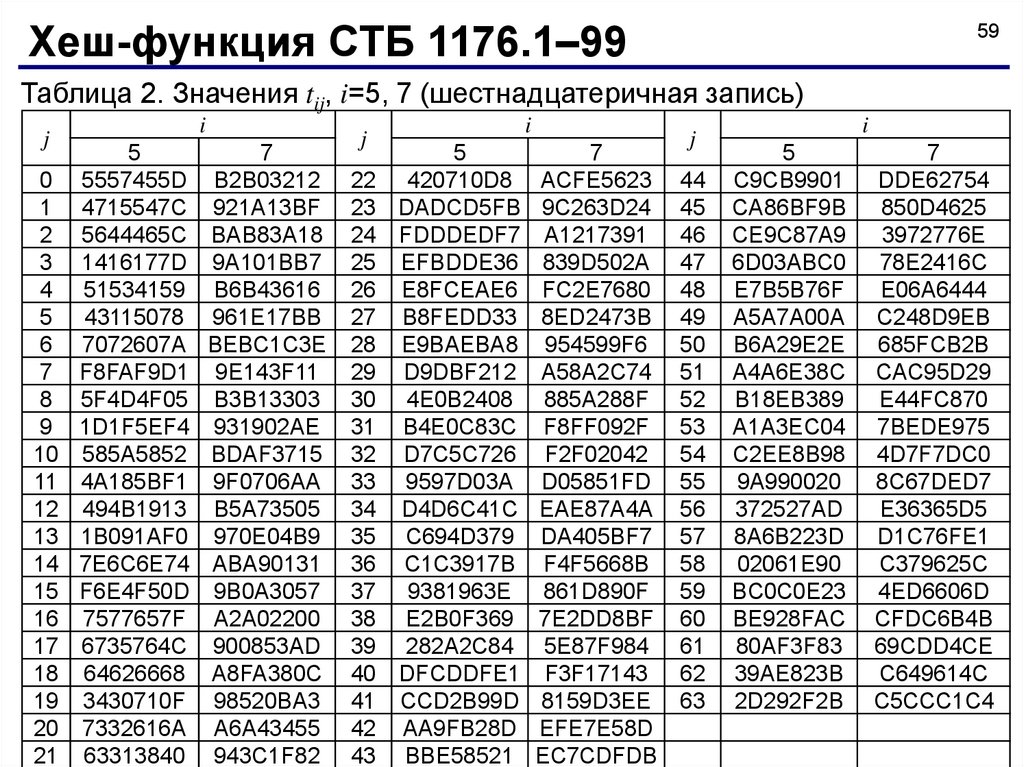
при выполнении алгоритма и заданы в табл. 1, 2
числами tij Z(32) так, что Ti=ti,63||…||ti,0.
Значения переменных T0, T2, T4, T6 определяются
числами rij Z(512): Ti=ri3 || ri2 || ri1 || ri0.

55.

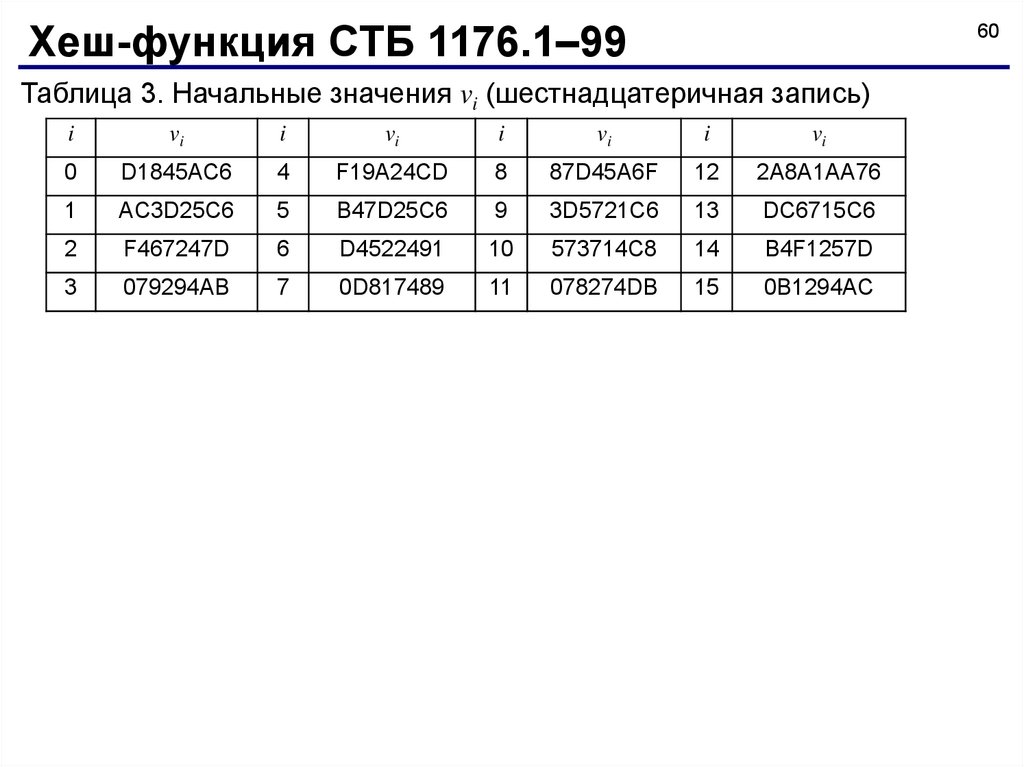
Хеш-функция СТБ 1176.1–99
Переменная V Z(512), V = v15||…||v1||v0, vi Z(32).
Начальные значения переменных vi указаны в табл.
3.
Переменная K Z(256), K = K1 || K0 = k7||…||k0,
где K0, K1 Z(128), Ki Z(32).
Переменная W Z(256), W = W1 || W0,
где W0, W1 Z(128).
55

56.

Хеш-функция СТБ 1176.1–99
Алгоритм.
Алгоритм вычисления хеш-значения h(M) состоит из
следующих шагов.
1. d 1
2. K Md
3. V (v15 [+] h7) ||…|| (v8 [+] h0) || (v7 [+] k7) ||…|| (v0 [+] k0)
4. Для i=0, 2, 4, 6 выполнить:
V 029(V), ri0 V
V 118(V), ri1 V
V 219(V), ri2 V
V 317(V), ri3 V
5. W K H
6. W0 (W0; T0, T1, T2, T3, T4, T5, T6, T7)
7. W1 (W1; T4, T1, T0, T3, T6, T5, T2, T7)
56

57.

Хеш-функция СТБ 1176.1–99
8. W 31(W)
9. W (H0, (H0, W))
10. W (K0, (K0, W))
11. W (H1, (H1, W))
12. W (K1, (K1, W))
13. H W
14. d d + 1
15. Если d < n + 2, то вернуться к шагу 2. Иначе перейти к
следующему шагу.
16. Вернуть H mod 2L
57

58.

Хеш-функция СТБ 1176.1–99
58
Таблица 1. Значения tij, i=1, 3 (шестнадцатеричная запись)
j
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
i
1
AA2AA82E
8A0A088E
A222A026
82020086
AE2CAC28
8C0E0C88
A624A420
84061E9A
AB2BA92F
8B0B098F
A323A127
B32133A7
8D0F9F1B
AF2D3FBB
07870583
17859D19
BA3AB83E
98381ABE
B231B025
806312A5
AD3DBF29
89B94B6F
3
4DCDCF4F
69E9EB6B
65E5E767
41C1C343
49C9CB4B
6DEDEF6F
61E1E363
45C5C747
5DDDCC4C
79F9E868
F17140C0
D55564E4
51D1C242
75F5EC6C
FD7D4ECE
D95960EA
5CDCDE5E
6AF8FA78
66E6E062
48C88C0C
7AA8AA28
8E0E4ACA
j
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
i
1
BD3CEF6A
CFBC1532
EB3BE96D
9B396BCD
B130E336
E11003B6
9E1C9C18
EACA4A6E
4EDF4C99
5E7FB481
E868FA6C
C8485ACE
E262E034
92424096
EE7EEC7A
DD0D1FCB
E666E460
971D4F93
FB697BED
C949DB4D
F36137F1
0173B771
3
53D3C444
FF7F6EEE
1C9CDF5F
2AB8FB7B
E2700181
9E0D7CAD
72F48357
46D0A92D
8D5B0FDB
F3747E91
54C6D456
20F0F222
2CFC1EFE
58D838BA
50D28052
30A0A232
3A825ADA
08889092
04D6D705
73A1ACAE
BC0AAB1D
8F2F842E
j
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
1
5B5C0459
CC5F5D16
47945291
35FEF813
F272787C
907058FC
147946B5
DAD9C267
E765E511
C0F0437D
F764C344
C6FFF9C4
F5775654
9545FD75
C1D8D376
C77441DE
D25351D0
C5D7D5F6
50D6D157
D455DCF4
i
3
188A8909
29B9F63D
A406F721
853F8677
07879515
23BBA32B
A5AF1A98
009A25BD
31B19303
0B19A7B5
3C3E14BF
B33927B7
1F117624
26948B35
991B9D97
9D34963B
3337B0BE
02101716
12A69FB4
B61336B2

59.

Хеш-функция СТБ 1176.1–99
59
Таблица 2. Значения tij, i=5, 7 (шестнадцатеричная запись)
j
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
i
5
5557455D
4715547C
5644465C
1416177D
51534159
43115078
7072607A
F8FAF9D1
5F4D4F05
1D1F5EF4
585A5852
4A185BF1
494B1913
1B091AF0
7E6C6E74
F6E4F50D
7577657F
6735764C
64626668
3430710F
7332616A
63313840
7
B2B03212
921A13BF
BAB83A18
9A101BB7
B6B43616
961E17BB
BEBC1C3E
9E143F11
B3B13303
931902AE
BDAF3715
9F0706AA
B5A73505
970E04B9
ABA90131
9B0A3057
A2A02200
900853AD
A8FA380C
98520BA3
A6A43455
943C1F82
j
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
i
5
7
420710D8 ACFE5623
DADCD5FB 9C263D24
FDDDEDF7 A1217391
EFBDDE36 839D502A
E8FCEAE6 FC2E7680
B8FEDD33 8ED2473B
E9BAEBA8 954599F6
D9DBF212 A58A2C74
4E0B2408 885A288F
B4E0C83C F8FF092F
D7C5C726 F2F02042
9597D03A D05851FD
D4D6C41C EAE87A4A
C694D379 DA405BF7
C1C3917B F4F5668B
9381963E 861D890F
E2B0F369 7E2DD8BF
282A2C84 5E87F984
DFCDDFE1 F3F17143
CCD2B99D 8159D3EE
AA9FB28D EFE7E58D
BBE58521 EC7CDFDB
j
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
i
5
C9CB9901
CA86BF9B
CE9C87A9
6D03ABC0
E7B5B76F
A5A7A00A
B6A29E2E
A4A6E38C
B18EB389
A1A3EC04
C2EE8B98
9A990020
372527AD
8A6B223D
02061E90
BC0C0E23
BE928FAC
80AF3F83
39AE823B
2D292F2B
7
DDE62754
850D4625
3972776E
78E2416C
E06A6444
C248D9EB
685FCB2B
CAC95D29
E44FC870
7BEDE975
4D7F7DC0
8C67DED7
E36365D5
D1C76FE1
C379625C
4ED6606D
CFDC6B4B
69CDD4CE
C649614C
C5CCC1C4

60.

Хеш-функция СТБ 1176.1–99
60
Таблица 3. Начальные значения vi (шестнадцатеричная запись)
i
vi
i
vi
i
vi
i
vi
0
D1845AC6
4
F19A24CD
8
87D45A6F
12
2A8A1AA76
1
AC3D25C6
5
B47D25C6
9
3D5721C6
13
DC6715C6
2
F467247D
6
D4522491
10
573714C8
14
B4F1257D
3
079294AB
7
0D817489
11
078274DB
15
0B1294AC

61.

Хеш-функция СТБ 1176.1–99
Концепция криптографии с открытыми ключами была
выдвинута
61