Хэш - функции (лекция 7)

1. Лекция 7.

ХЭШ-ФУНКЦИИ
1. Основные понятия
2. Коллизии
3. Алгоритм SHA-1

2.

Криптографическая хэш-функция h — это функция,
определенная на битовых строках произвольной длины со
значениями строк битов фиксированной длины.
Хеширование (hashing) — преобразование
по детерминированному алгоритму входного массива
данных произвольной длины в выходную битовую строку
фиксированной длины.
Такие преобразования также называются хэш функциями или функциями свёртки, а их результаты
называют хэш-кодом или сверткой сообщения.
Хэш - функции произвольного вида принадлежат к
классу однонаправленных функций без потайного хода.
Хэш-код создается функцией Н: h = H (M),
где М - сообщение произвольной длины
h - хэш-код фиксированной длины.

3.

В криптографии хэш-функции применяются для задач:
— построения систем контроля целостности данных при их передаче или
хранении,
— аутентификации источника данных.
При решении первой задачи для каждого набора данных вычисляется
значение хэш-функции (код аутентификации сообщения,
имитовставка), которое передается или хранится вместе с самими
данными. При получении данных пользователь вычисляет значение
свертки и сравнивает его с имеющимся контрольным значением.
Несовпадение говорит о том, что данные были изменены. Для выработки
имитовставки обычно применяют хэш-функции, значение которых
зависит от секретного ключа пользователя. Этот ключ должен быть
известен передающей и проверяющей сторонам. Такие хэш-функции
называют ключевыми.
Имитовставки, формируемые с помощью ключевых хэш-функций, не
должны позволять противнику создавать поддельные (сфабрикованные)
сообщения (fabrication) при атаках типа имитация (impersonation) и
модифицировать передаваемые сообщения (modification)при атаках
типа подмена (substitution).

4.

При решении второй задачи - аутентификации источника
данных, обмен данными происходит между не доверяющими
друг другу сторонами. В такой ситуации применяют схемы
цифровой подписи, позволяющие осуществлять
аутентификацию источника данных. Как правило, при этом
сообщение, прежде чем быть подписано личной подписью,
основанной на секретном ключе пользователя, "сжимается" с
помощью хэш-функции, выполняющей функцию кода
обнаружения ошибок. В данном случае хэш-функция не зависит
от секретного ключа и может быть фиксирована и известна
всем. Основными требованиями к ней являются гарантии
невозможности подмены подписанного документа, а также
подбора двух различных сообщений с одинаковым значением
хэш-функции

5. Классификация хэш-функций

Криптографические хэш-функции
разделяются на два класса:
- хэш-функции без ключа (MDC (Modification
(Manipulation) Detect Code) - коды),
- хэш-функции c ключом (MАC (Message
Authentication Code) - коды).
Хэш-функции разделяются на два подкласса:
- слабые хэш-функции,
- сильные хэш-функции

6. Схема Меркеля – Дамгарда

Наиболее распространенной криптографической функцией
хэширования на основе одношаговой функции сжатия является
итеративная схема Меркеля – Дамгарда.
В конец хэшируемого сообщения M приписывается длина
сообщения и дополнение, так чтобы длина увеличенного
сообщения была кратна числу m, где m – длина строки, которую
может обработать функция сжатия.
Пусть сообщение разбито на t m-битовых блоков (строк): M1,
M2,…, Mt .
Свертки, получаемые в ходе итераций, обозначим H1, H2,..., Ht ,
результирующая свертка всего сообщения H (M).

7.

Последовательная процедура вычисления свертки:
Н0 = v
Нi = f (Mi , Hi-1 )
(*)
h(M) = НN
Здесь:
М = (M1 , M2 , …, MN ) – некоторое сообщение, разделенные на
части одинаковой длины | Mi |= m
(при необходимости конец сообщения дополняется до нужной
длины)
v – начальный вектор (для ключевых хэш-функций обычно 0,
для бесключевых выбирается случайным образом )

8. Ключевые хэш-функции

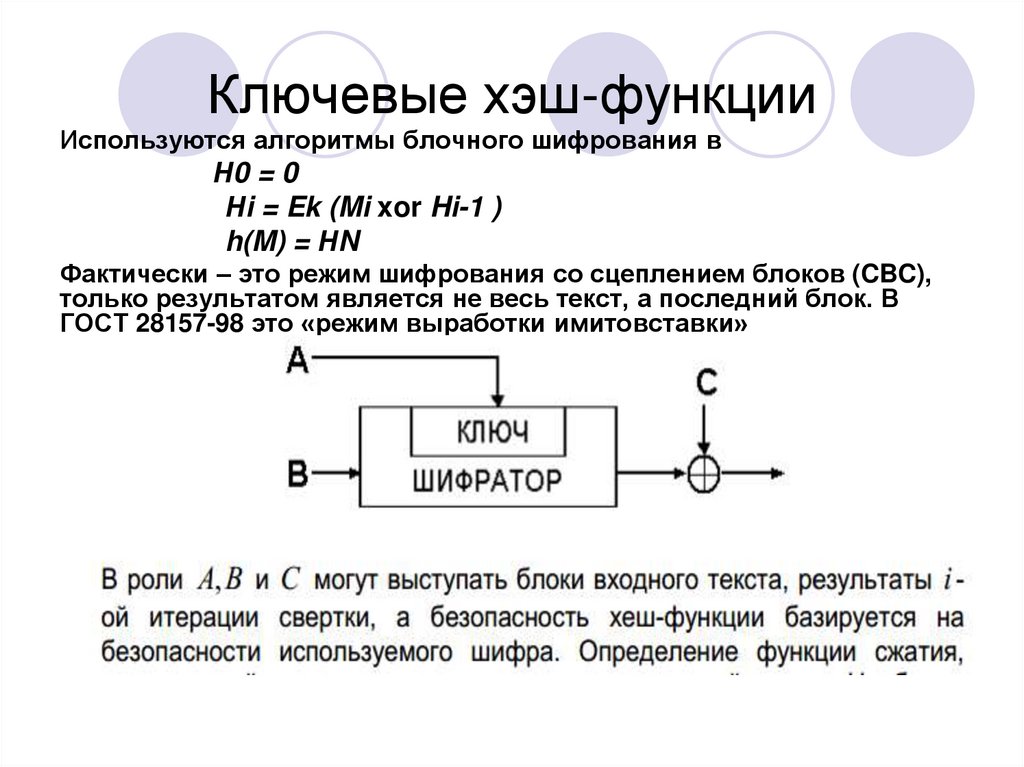
Используются алгоритмы блочного шифрования в
Н0 = 0
Нi = Ek (Mi xor Hi-1 )
h(M) = НN
Фактически – это режим шифрования со сцеплением блоков (CBC),
только результатом является не весь текст, а последний блок. В
ГОСТ 28157-98 это «режим выработки имитовставки»

9.

10. Бесключевые хэш-функции

Большинство известных бесключевых ХФ основано на
разбиении произвольно длинных сообщений на
блоки фиксированной длины и их последовательной
обработке криптографической ХФ. Этот метод
называется итеративным хэшированием.
Пример
где
Н0
– произвольное начальное число.

11.

12. Требования к хэш-функциям

1.
2.
3.
4.
5.
6.
Хэш-функция Н должна применяться к блоку
данных любой длины.
Хэш-функция Н создает выход фиксированной
длины.
Н (М) относительно легко (за полиномиальное
время) вычисляется для любого значения М.
Для любого данного значения хэш-кода h
вычислительно невозможно найти M такое, что Н
(M) = h.
Для любого данного х вычислительно невозможно
найти y, не равный x, что H (y) = H (x).
Вычислительно невозможно найти произвольную
пару (х, y) такую, что H (y) = H (x).

13.

Первые три свойства требуют, чтобы хэшфункция создавала хэш-код для любого сообщения.
Четвертое свойство определяет требование
односторонности хэш-функции: легко создать хэш-код по
данному сообщению, но невозможно восстановить
сообщение по данному хэш-коду. Это свойство важно, если
аутентификация с использованием хэш-функции включает
секретное значение. Само секретное значение может не
посылаться, тем не менее, если хэш-функция не является
односторонней, противник может легко раскрыть секретное
значение следующим образом. При перехвате передачи
атакующий получает сообщение М и хэш-код С = Н (SAB ||
M). Если атакующий может инвертировать хэш-функцию, то,
следовательно, он может получить SAB || M = H-1 (C). Так как
атакующий теперь знает и М и SAB || M, получить SAB
совсем просто.

14.

Пятое свойство гарантирует, что невозможно найти
другое сообщение, чье значение хэш-функции совпадало бы
со значением хэш-функции данного сообщения. Это
предотвращает подделку аутентификатора при
использовании зашифрованного хэш-кода. Если данное
свойство не выполняется, атакующий имеет возможность
выполнить следующую последовательность действий:
перехватить сообщение и его зашифрованный хэш-код,
вычислить хэш-код сообщения, создать альтернативное
сообщение с тем же самым хэш-кодом, заменить исходное
сообщение на поддельное. Поскольку хэш-коды этих
сообщений совпадают, получатель не обнаружит подмены.
Хэш-функция, которая удовлетворяет первым пяти
свойствам, называется простой или слабой хэшфункцией.
Если кроме того выполняется шестое свойство, то такая
функция называется сильной хэш-функцией.

15.

Не доказано существование необратимых хэшфункций, для которых вычисление какого-либо
прообраза заданного значения хэш-функции
теоретически невозможно. Обычно нахождение
обратного значения является лишь вычислительно
сложной задачей.
В общем случае однозначного соответствия между
исходными данными и хеш-кодом нет из-за того, что
количество значений хеш-функций всегда меньше,
чем вариантов входных данных. Следовательно,
существует множество входных сообщений, дающих
одинаковые хеш-коды (такие ситуации
называются коллизиями ). Вероятность
возникновения коллизий играет немаловажную роль
в оценке качества хеш-функций.

16.

Простейшая хеш-функция может быть составлена с
использованием операции "сумма по модулю 2" следующим
образом: получаем входную строку, складываем все байты по
модулю 2 и байт-результат возвращаем в качестве значения
хеш-фукнции. Длина значения хеш-функции составит в этом
случае 8 бит независимо от размера входного сообщения.
Например, пусть исходное сообщение, переведенное в
цифровой вид, было следующим (в шестнадцатеричном
формате): 3E 54 A0 1F B4
Переведем сообщение в двоичный вид, запишем байты друг
под другом и сложим биты в каждом столбике по модулю 2:
0011 1110
0101 0100
1010 0000
0001 1111
1011 0100
---------0110 0101
Результат ( 0110 0101(2) или 65(16) ) и будет значением хешфункции.

17.

Однако такую хеш-функцию нельзя использовать для
криптографических целей, например для формирования
электронной подписи, так как достаточно легко изменить
содержание подписанного сообщения, не меняя значения
контрольной суммы.
Поэтому рассмотренная хеш-функция не годится для
криптографических применений. В криптографии хеш-функция
считается хорошей, если трудно создать два прообраза с
одинаковым значением хеш-функции, а также, если у выхода
функции нет явной зависимости от входа.
Для криптографических хэш-функций также важно, чтобы при
малейшем изменении аргумента значение функции сильно
изменялось (лавинный эффект). В частности, значение хеша не
должно давать утечки информации даже об отдельных битах
аргумента. Это требование является залогом криптостойкости
алгоритмов хэширования, хэширующих пользовательский пароль
для получения ключа.

18. Контрольные суммы

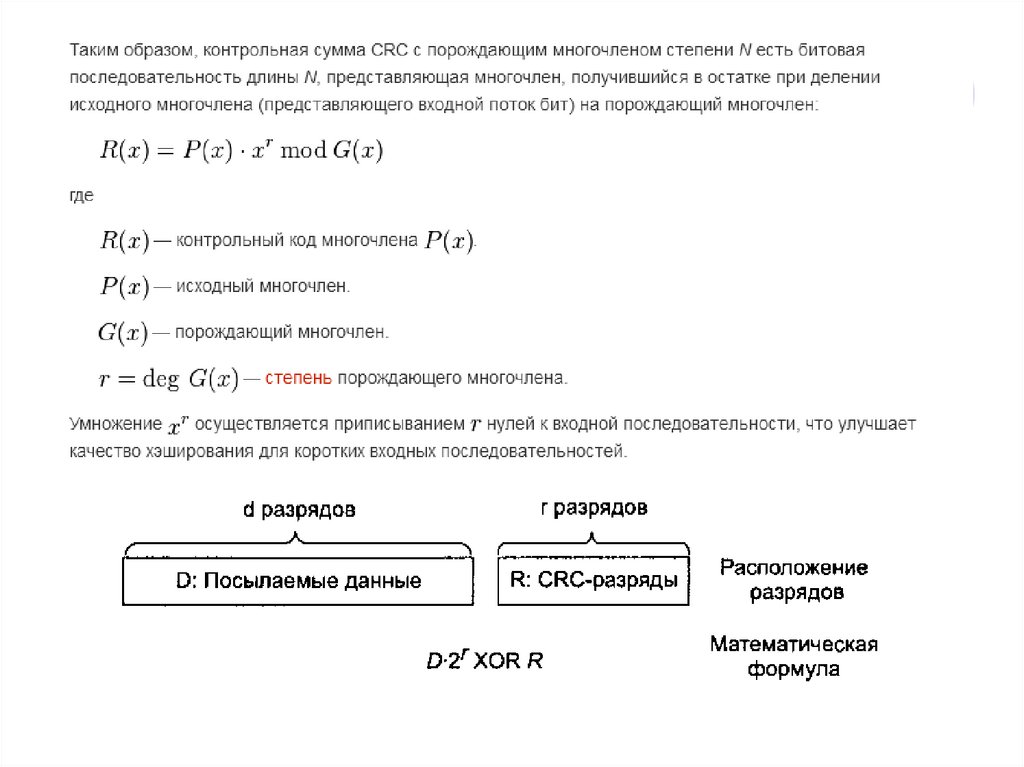
Алгоритм вычисления контрольной суммы (CRC, cyclic redundancy
check, проверка избыточности циклической суммы) — способ
цифровой идентификации некоторой последовательности данных,
который заключается в вычислении контрольного значения её
циклического избыточного кода.
С точки зрения математики КС является типом хэш-функции,
используемой для вычисления контрольного кода — небольшого
количества бит внутри большого блока данных, например сетевого
пакета или блока компьютерного файла, применяемого для
обнаружения ошибок при передаче или хранении информации.
Результат вычисления КС добавляется в конец блока данных
непосредственно перед началом передачи или сохранения данных на
каком-либо носителе информации. Впоследствии он проверяется для
подтверждения её целостности.
Популярность КС обусловлена тем, что подобная проверка просто
реализуема двоичном цифровом оборудовании, легко анализируется,
и хорошо подходит для обнаружения общих ошибок, вызванных
наличием шума в каналах передачи данных. Он широко используется в
проводных и беспроводных сетях, и в устройствах хранения данных,
для проверки информации на подлинность и защиты от
несанкционированного изменения.

19. Циклический избыточный код CRC (Cyclic redundancy code)

Циклический избыточный код CRC (Cyclic redundancy code)
Алгоритм CRC базируется на свойствах деления с остатком двоичных
многочленов, т.е. хэш-функция является по остатком от
деления многочлена, соответствующего входным данным, на некий
фиксированный порождающий многочлен.
В виде двоичного многочлена может быть представлен любой из
блоков обрабатываемых данных, и любой двоичный многочлен
обращается в набор битов. Количество различных многочленов
степени меньше N равно 2N, что совпадает с числом всех двоичных
последовательностей длины N.
При делении с остатком степень многочлена остатка строго меньше
степени многочлена делителя, т.е. если в качестве делителя выбрать
многочлен степени N, то различных остатков от деления он будет
давать как раз 2N,
При "правильном" выборе порождающего многочлена (делителя),
остатки от деления на него будут обладать нужными
свойствами хэширования - хорошей перемешиваемостью и быстрым
алгоритмом вычисления. Второе обеспечивается тем, что степень
порождающего многочлена обычно пропорциональна длине байта
или машинного слова (например 8, 16 или 32).

20.

21.

В зависимости от вида порождающего многочлена и его длины, изменяется
вероятность совпадения контрольных сумм для различных исходных данных и
время контрольного суммирования. Наиболее популярными являются
алгоритмы CRC, работающие с порождающими многочленами: восьмой (CRC8), шестнадцатой (CRC - 16) и тридцать второй (CRC – 32) степени.
Выбор длины порождающего многочлена, кратной байту, позволяет ускорить
работу программы по контрольному суммированию, обеспечивая достаточную
надежность полученного результата. Например, контрольное суммирование
CRC-32 в пределе позволяет получить надежность порядка: 232 = 4.294.967.296.
Что в принципе позволяет, практически со 100% вероятностью, обнаруживать
сбои при хранении и передаче данных.
Существует достаточно большое разнообразие порождающих многочленов для
алгоритмов контрольного суммирования CRC – 8, 16 и 32, подобранных на
основе теории кодирования и многочисленных исследований.
CRC-8: x8 + x7 + x6 + x4 + x2 + 1 -Используется формой Dallas Semiconductor в
устройствах низкоскоростной связи.
CRC-16: x16 + x15 + x2 + 1 - используется в таких интерфейсах, как USB, ModBus
и других линиях связи.
CRC-32: x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 используется при кодировании видео и аудио сигналов с использованием
стандарта MPEG-2, при кодировании растровых изображений в формате PNG и
во многих других случаях.

22. Коллизии

Коллизией хеш-функции называется два различных входных блока
данных х и у таких, что
Коллизии существуют для большинства хеш-функций, но для
«хороших» хеш-функций частота их возникновения близка к
теоретическому минимуму.
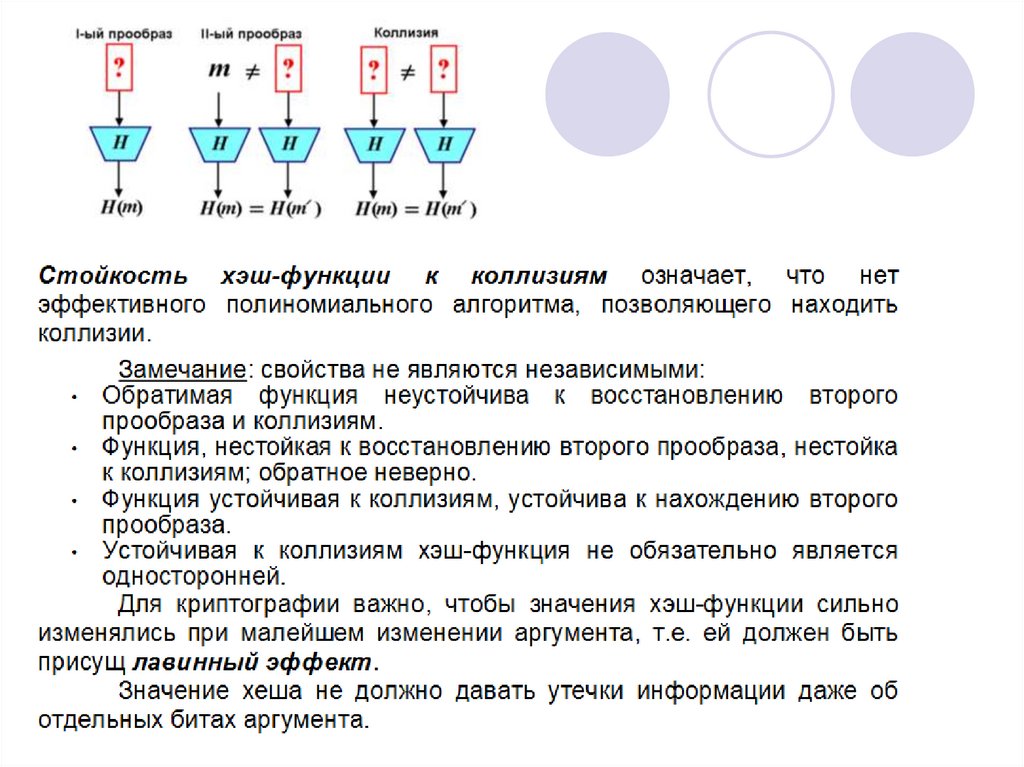
Для того, чтобы хеш-функция H считалась криптографически
стойкой, она должна удовлетворять трём основным требованиям, на
которых основано большинство применений хеш-функций в
криптографии:
•Необратимость: для заданного значения хеш-функции m должно
быть практически невозможно найти блок данных
, для
которого
.
•Стойкость к коллизиям первого рода: для заданного
сообщения M должно быть практически невозможно подобрать
другое сообщение N, для которого
.
•Стойкость к коллизиям второго рода: должно быть практически
невозможно подобрать пару сообщений
, имеющих
одинаковый хеш.

23.

24. Использование коллизий для взлома

В качестве примера можно рассмотреть простую
процедуру аутентификации пользователя:
при регистрации в системе пользователь вводит свой пароль, к
которому применяется некоторая хеш-функция, значение
которой записывается в базу данных;
при каждом вводе пароля, к нему применяется та же хешфункция, а результат сравнивается с тем, который записан в
БД.
При таком подходе, даже если злоумышленник получит доступ к
базе данных, он не сможет восстановить исходные пароли
пользователей (при условии необратимости используемой хешфункции). Однако, если злоумышленник умеет находить
коллизии для используемой хеш-функции, ему не составит
труда найти поддельный пароль, который будет иметь ту
же хеш-сумму, что и пароль пользователя.
Можно использовать коллизии для подделки сообщений:
информация о валютных операциях, к примеру, часто
шифруется посредством хеш-функций; злоумышленник,
обладая методом нахождения коллизий этой хеш-функции,
может заменить сообщение поддельным и тем самым повлиять
на ход валютной операции.

25. Защита от использования коллизий

Существует ряд методов защиты от взлома, защиты
от подделки паролей, подписей и сертификатов, даже если
злоумышленнику известны методы построения коллизий для
какой-либо хеш-функции.
Одним из методов является метод «salt», применяемый при
хранении UNIX-паролей — добавление некоторой
последовательности символов перед хешированием. Иногда,
эта же последовательность добавляется и к полученному хешу.
После такой процедуры итоговые хеш-таблицы значительно
сложнее анализировать, а так как эта последовательность
секретна, существенно повышается сложность построения
коллизий — злоумышленнику должна быть также известна
последовательность «salt».
Другим методом является конкатенация хешей, получаемых от
двух различных хеш-функций. При этом, чтобы подобрать
коллизии к хеш-функции
, являющейся
конкатенацией хеш-функций
и
, необходимо
знать методы построения коллизий и для
, и
.
Недостатком конкатенации является увеличение размера хеша,
что не всегда приемлемо в практических приложениях.

26. Методы поиска коллизий

Атака «дней рождения» позволяет находить коллизии для хешфункции с длиной значений n битов в среднем за примерно 2n / 2
вычислений хэш-функции. Поэтому n-битная хеш-функция
считается криптостойкой, если вычислительная сложность
нахождения коллизий для неё близка к 2n / 2.
Парадокс дней рождения — утверждение, что если дана группа
из 23 или более человек, то вероятность того, что хотя бы у двух
из них дни рождения (число и месяц) совпадут, превышает 50 %.
Для группы из 60 или более человек вероятность совпадения дней
рождения хотя бы у двух её членов составляет более 99 %, хотя
100 % она достигает, когда в группе не менее 366 человек (с
учётом високосных лет — 367).
Проводим аналогию: человек - своего рода вход для хешфункции, день рождения - хеш-значение. В этом случае аналог
совпадения дней рождения - коллизия.

27.

Применяя так называемый "парадокс дня рождения" к слабым-хэш
функциям формулируется следующая задача:
Предположим, количество выходных значений хэш-функции Н равно n.
Каким должно быть число k, чтобы для конкретного значения X и
значений Y1, …, Yk вероятность того, что хотя бы для одного Yi
выполнялось равенство
H (X) = H (Y) была бы больше 0,5?
k = n/2
для m-битового хэш-кода достаточно выбрать 2m-1 сообщений, чтобы
вероятность совпадения хэш-кодов была больше 0,5.
На практике это означает следующее, возьмём к примеру слабую хэшфункцию MySQL(64bit) всё множество её значений
2^64=18446744073709551616 вариантов. Чтоб найти совпадение с
исходным паролем с вероятностью 50% нам требуется подать на вход
2^63=2^64/2=18446744073709551616/2=9223372036854775808
случайных паролей, т.е. ровно половину.
Примем среднюю скорость вычислений одного хеша 8 000 000 000 000
п/c. на GF8600GT получим время 1152921сек.~320часов.~13 дней. Что
это означает? Это означает что мы можем не искать исходный пароль,
последовательно подавая на вход пароли, генерируемые простым
брутфорсом (последовательно) а подавать случайное значение пароля
из широкого диапазона > чем число возможных хэшей и в 50% через
13 дней непрерывного брута мы получаем хэш, который совпадёт с
хэшем от исходного пароля (а может это будет и оригинальный
пароль).

28.

29. Хэш-функция SHA-1

Алгоритм получает на входе сообщение максимальной
длины 264 бит и создает в качестве выхода дайджест сообщения
длиной 160 бит.

30.

Шаг 1: добавление недостающих битов
Сообщение добавляется таким образом, чтобы его длина была
кратна 448 по модулю 512 (длина 448 mod 512). Добавление
осуществляется всегда, даже если сообщение уже имеет нужную
длину. Таким образом, число добавляемых битов находится в
диапазоне от 1 до 512.
Добавление состоит из единицы, за которой следует
необходимое количество нулей.
Шаг 2: добавление длины
К сообщению добавляется блок из 64 битов. Этот блок
трактуется как беззнаковое 64-битное целое и содержит длину
исходного сообщения до добавления.
Результатом первых двух шагов является сообщение, длина
которого кратна 512 битам. Расширенное сообщение может быть
представлено как последовательность 512-битных блоков Y0, Y1, .
. . , YL-1, так что общая длина расширенного сообщения есть L *
512 бит. Таким образом, результат кратен шестнадцати 32-битным
словам.
Пример 1. На вход алгоритма хеширования SHA-1 подается
сообщение длиной 2590 битов. Сколько битов будет содержать
дополнение сообщения? m +s +64 ≡ 0(mod512) ⇒ − s− m =
64(mod512) s = − 2590−64 (mod512) = −2654(mod512) ≡ 418.
Дополнение состоит из одной 1 и 417 нулей.

31.

Шаг 3: инициализация SHA-1 буфера
Используется 160-битный буфер для хранения
промежуточных и окончательных результатов хэш-функции.
Буфер может быть представлен как пять 32-битных
регистров A, B, C, D и E. Эти регистры инициализируются
следующими шестнадцатеричными числами:
A = 67452301
B = EFCDAB89
C = 98BADCFE
D = 10325476
E = C3D2E1F0
Вектор инициализации, подаваемый на вход 1-го
раунда – результат конкатенации SHA0= A ||B|| C|| D|| E
.

32.

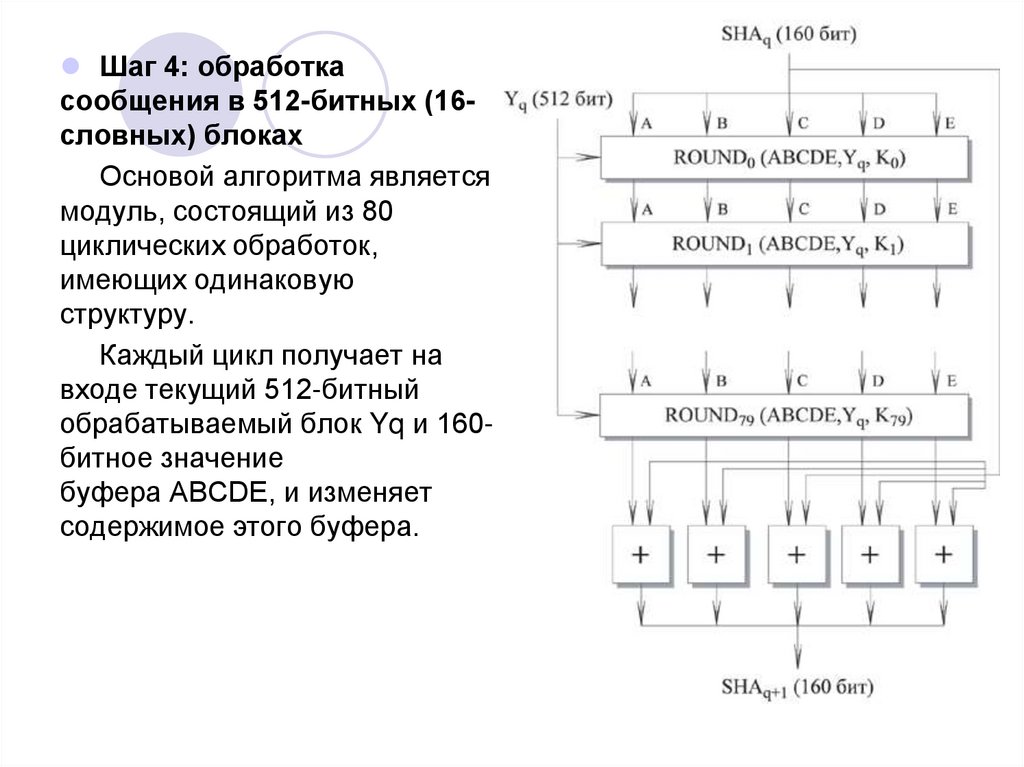
Шаг 4: обработка
сообщения в 512-битных (16словных) блоках
Основой алгоритма является
модуль, состоящий из 80
циклических обработок,
имеющих одинаковую
структуру.
Каждый цикл получает на
входе текущий 512-битный
обрабатываемый блок Yq и 160битное значение
буфера ABCDE, и изменяет
содержимое этого буфера.

33.

В каждом цикле используется дополнительная константа Кt,
Для получения SHAq+1 выход 80-го цикла
складывается со значением SHAq. Сложение по
модулю 232 выполняется независимо для каждого из
пяти слов в буфере с каждым из соответствующих
слов в SHAq.
Шаг 5: выход
После обработки всех 512-битных блоков
выходом L-ой стадии является 160-битный
дайджест сообщения.

34.

Рассмотрим более детально логику в каждом из 80 циклов
обработки одного 512-битного блока. Каждый цикл можно
представить в виде:
ТЕМР(A, B, C, D, E, Wt , Kt) = CLS5 (A) + ft (B, C, D) + E + Wt + Kt,
E = D; D = C; C = CLS30 (B); B = A; A = ТЕМР
где
A, B, C, D, E - пять слов из буфера.t - номер цикла, 0 t 79.
ft - элементарная логическая функция.
CLSs - циклический левый сдвиг 32-битного аргумента на s
битов.
Wt - 32-битное слово, полученное из текущего входного 512битного блока.
Kt - дополнительная константа.
+ - сложение по модулю 232.
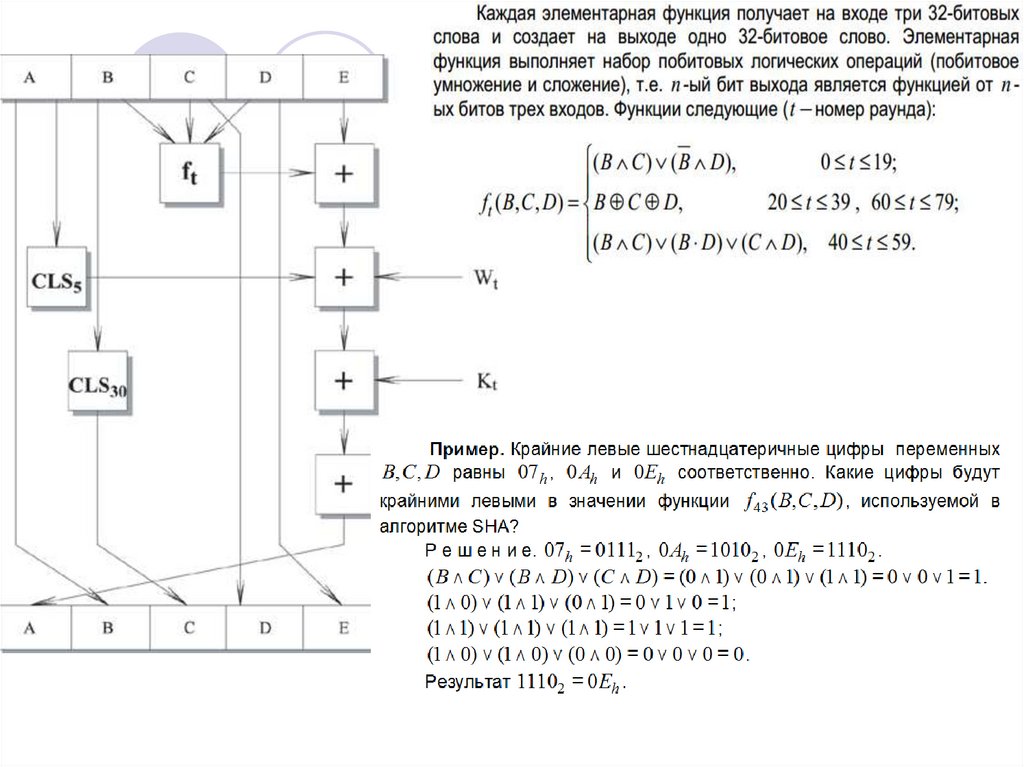
Логика выполнения отдельного шага:

35.

36.

32-битные слова Wt получаются из очередного 512-битного
блока сообщения следующим образом.
Wt= Yt , при t = 0,1,...,15; 1
Wt = CLS1(Wt −3⊕Wt−8⊕Wt−14⊕Wt−16 ) при t =16,...,79, где
CLS1– операция циклического сдвига аргумента на один разряд
влево.

37.

Алгоритм SHA-1 можно суммировать следующим образом:
SHA0 = IV
SHAq+1 = Σ32 (SHAq , ABCDEq )
SHA = SHAL-1
Где
IV - начальное значение буфера ABCDE.
ABCDEq - результат обработки q-того блока сообщения.
L - число блоков в сообщении, включая поля добавления и
длины.
Σ32 - сумма по модулю 232, выполняемая отдельно для каждого
слова буфера.
SHA - значение дайджеста сообщения.

38. MD5

39.  ГОСТ Р 34.11 — 2012

ГОСТ Р 34.11 — 2012
Размер хеша: 256 или 512 бит
Размер блока входных данных: 512 бит
Концепции построения
не должно быть свойств, которые позволяли бы применить
известные атаки.
должны использоваться изученные конструкции и
преобразования.
Вычисление хеш-функции должно быть эффективным,
занимать мало времени.
Не должно быть лишних преобразований, усложняющих
конструкцию хеш-функции. Причем каждое используемое в хешфункции преобразование должно отвечать за определенные
криптографические свойства.

40.

В основу хеш-функции положена итерационная конструкция МерклаДамгарда с использованием MD-усиления. Под MD-усилением
понимается дополнение неполного блока при вычислении хешфункции до полного путем добавления вектора (0 … 01) такой длины,
чтобы получился полный блок. Из дополнительных элементов нужно
отметить следующие:
Завершающее преобразование, которое заключается в том, что
функция сжатия применяется к контрольной сумме всех блоков
сообщения по модулю 2512.
При вычислении хеш-кода на каждой итерации применяются разные
функции сжатия. Можно сказать, что функция сжатия зависит от
номера итерации.