vektory_v_prostranstve

1.

Векторы в пространстве
вход

2.

Понятие вектора в пространстве
Вектор(направленный отрезок) –
отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0

3.

Коллинеарные векторы
Два ненулевых вектора называются коллинеарными,
если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы

4.

Сонаправленные векторы
Сонаправленные векторы - векторы, лежащие
по одну сторону от прямой, проходящей через их
начала.
a
a b
b
Нулевой вектор считается сонаправленным с
любым вектором.
• Равные векторы

5.

Равные векторы
Равные векторы - сонаправленные векторы,
длины которых равны.
a
a b a b , a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.

6.

Противоположно направленные
векторы
Противоположно направленные векторы –
векторы, лежащие по разные стороны от прямой,
проходящей через их начала.
a
a b
b
Противоположные векторы

7.

Противоположные векторы
Противоположные векторы – противоположно
направленные векторы, длины которых равны.
a
a b a b , a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.

8.

Признак коллинеарности
Если существует
такое число k при котором
выполняетс я равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы .
Доказательство

9.

Доказательство признака
коллинеарности
Два вектора a и b коллинеарн ы тогда и
только тогда , когда имеет место равенство
a kb
вектор
k a b , если k 0
( следует
из определени
вектор
k a b , если k 0
произведен
ия вектора
Значит вектор b и k a коллинеарн ы ,
т . к . сонаправле нные и противолож
но
направленн ые векторы лежат на одной
или параллельн ых прямых .
ч . т .д .
я
на число )

10.

Определение компланарных
векторов
Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB 1 , AC, AC 1 компланарн ы, т.к.
BB 1 AA 1 , а векторы AA 1 , AC , AC 1
лежат в плоскости (AA 1 C)

11.

О компланарных векторах
Любые два вектора всегда компланарны.
α
a
b
a
b
a
b
a и b компланарн
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb
ы

12.

Признак компланарности
Если вектор c можно разложить по векторам
а и b , т .е. представит ь в виде
с xa yb
где х и у некоторые числа , то векторы a , b
и c компланарн ы .
Доказательство
Задачи

13.

Задачи на компланарность
1)
2)
Компланарны ли векторы:
а) a , b , 2 a , 3 b ;
б) a , b , a b , a b ?
Справка
Решение
Известно, что векторы a , b и c компланарны.
Компланарны ли векторы:
а) a , 2 b , 3 c ;
б) a b , a 2 c , 2 b 3 c ?
Справка
Решение

14.

Решение
а )векторы a и 2 a коллинеарн ы,
векторы b и 3b коллинеарн ы,
значит векторы a , b, 2 a и 3b компланарн ы
б )векторы a , b и a b компланарн ы,
векторы a , b и a b компланарн ы,
значит векторы a , b, a b и a b компланарн ы

15.

Решение
a) если векторы a , 2 b , 3 c компланарн ы,
то существуют такие х и у, что
a xb y c
проверяем существуют ли такие т и п, что
a m 2b n 3c
имеем :
x
2m x m
2
y
3n y n
3
m и п определяют ся единственн ым образом,
значит векторы компланарн ы

16.

Решение
a b,a 2c,2b 3c
б)если векторы
такие
ы, то существуют
компланарн
a b x( a 2 c ) y(2 b 3 c )
a b x a 2x c 2y b 3y c
a (1 x) b (1 2y) c ( 2x 3y) 0
1 x 0 x 1
1
1 2y 0
y
3y 2x 0
2
1
a b a 2 c (2 b 3 c )
2
,
х и у существуют
искомые
ы
компланарн
векторы
значит
х и у, что

17.

Доказательство признака
компланарности
B1 OC xOA yOB
С
с xa yb
c
B
b
x , y некоторые числа
A
Доказать :
A1
O
Дано :
a
a , b и с компланарн ы
Доказательство :
Пусть a и b не коллинеарны
О произвольная точка
OA a , OB b
OA,OB ,OA1 ,OB1 (OAB)
OA1 x OA OB1 y OB
OC c OA1 OB1 x OA y OB
OA a ,OB b ,OC c лежат в одной плоскости
a ,b ,c компланарны ч.т.д

18.

Свойство компланарных
векторов
Если векторы a , b и c компланарн ы , то один из них
можно выразить линейным образом через два других ,
т .е . представит ь в виде :
с xa yb
причем коэффициен ты разложения
определяют ся единственн ым образом .

19.

Действия с векторами
Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

20.

Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения

21.

Правило треугольника
Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А вектор
AB , равный а
2. от точки В отложить
вектор
BC , равный
3. вектор
суммой
векторов
AC называется
B
a
a
b
А
b
a b
C
b
aиb

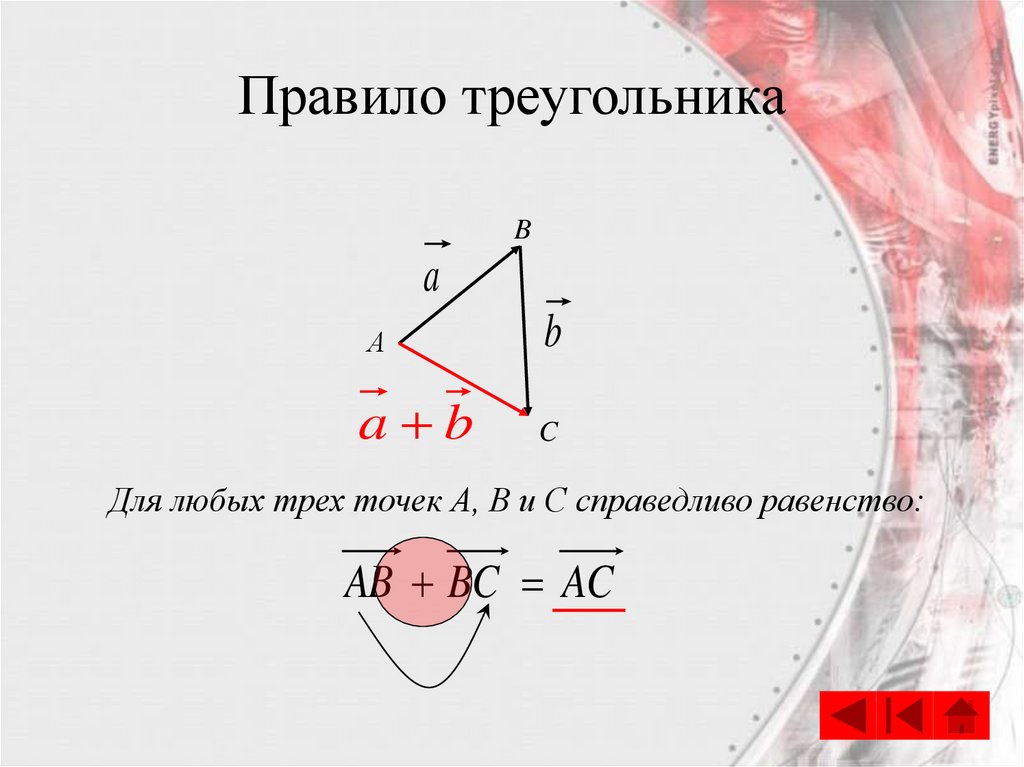
22.

Правило треугольника
B
a
А
b
a b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC

23.

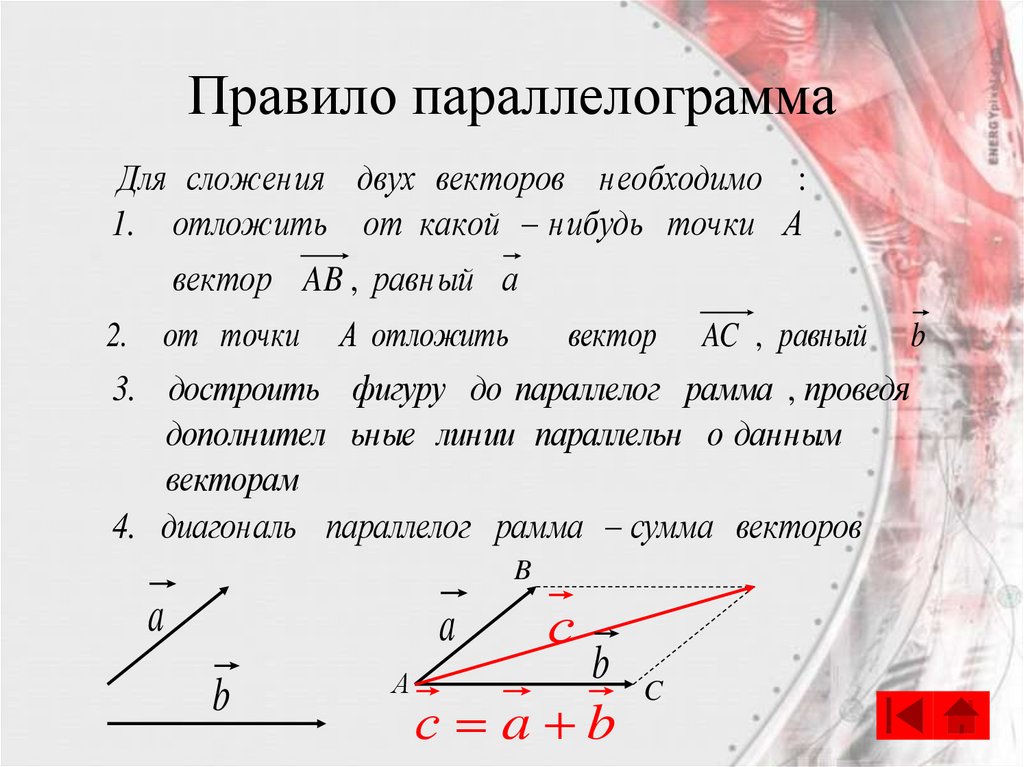
Правило параллелограмма
Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB , равный а
2.
от точки
А отложить
вектор
AC , равный
3. достроить фигуру до параллелог рамма , проведя
дополнител ьные линии параллельн о данным
векторам
4. диагональ параллелог рамма сумма векторов
B
a
a
b
А
с
b
с a b
C
b

24.

Свойства сложения
Для любых векторов
равенства :
a , b и c справедлив ы
a b b a
переместит
ельный
закон
a b с а b с сочетатель ный закон

25.

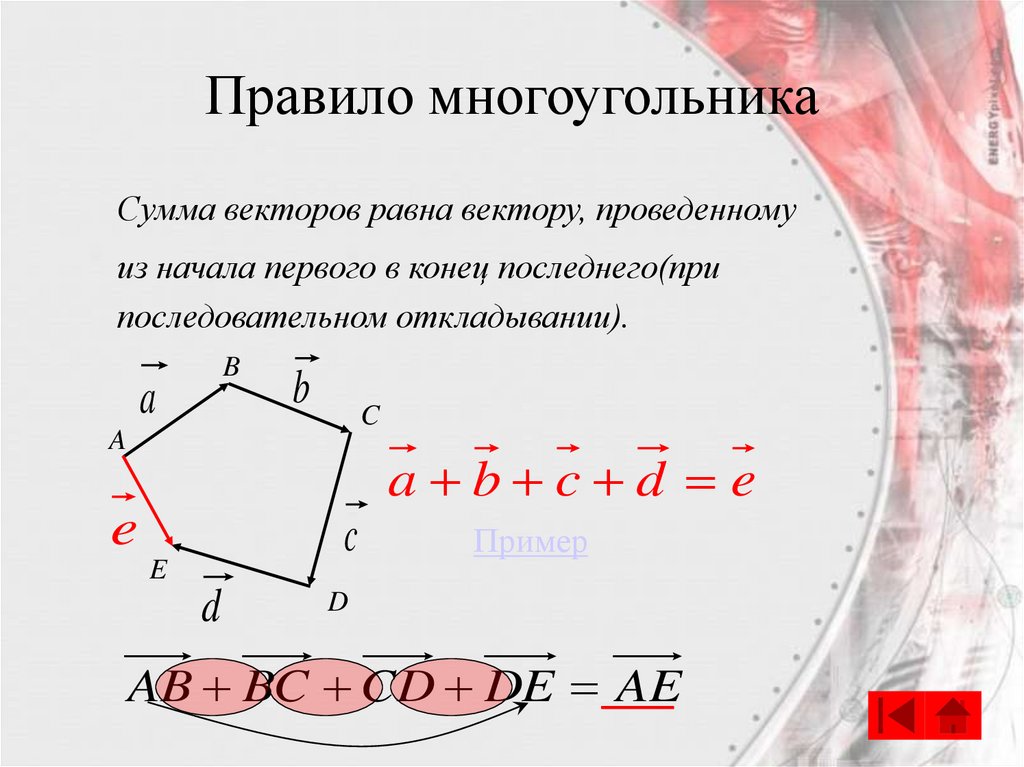
Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
B
a
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE

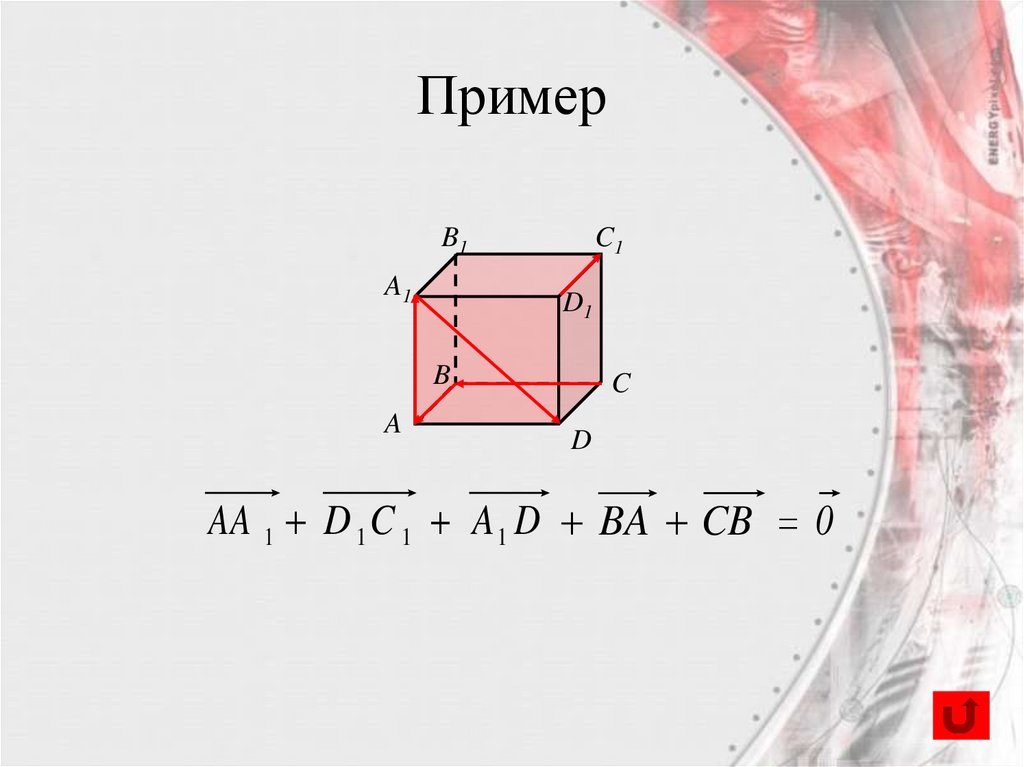
26.

Пример
B1
A1
C1
D1
B
A
C
D
AA 1 D 1 C 1 A 1 D BA CB 0

27.

Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B1
A1
C1
d
AB b
D1
с bB
C
А
a
AD a
D
AC 1 AD AB AA 1
AA1 c
AC1 d

28.

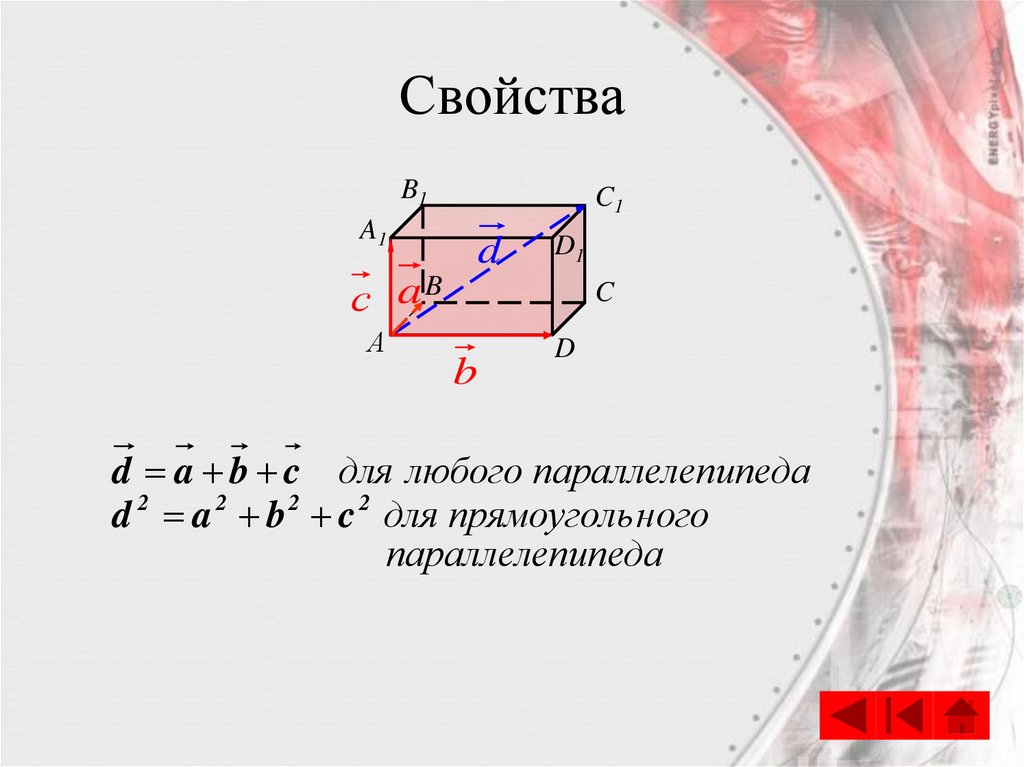
Свойства
B1
C1
A1
d
D1
с aB
А
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда

29.

Вычитание векторов
• Вычитание
• Сложение с противоположным

30.

Вычитание
Разностью векторов a и b называется такой
вектор, сумма которого с вектором b равна
вектору a .

31.

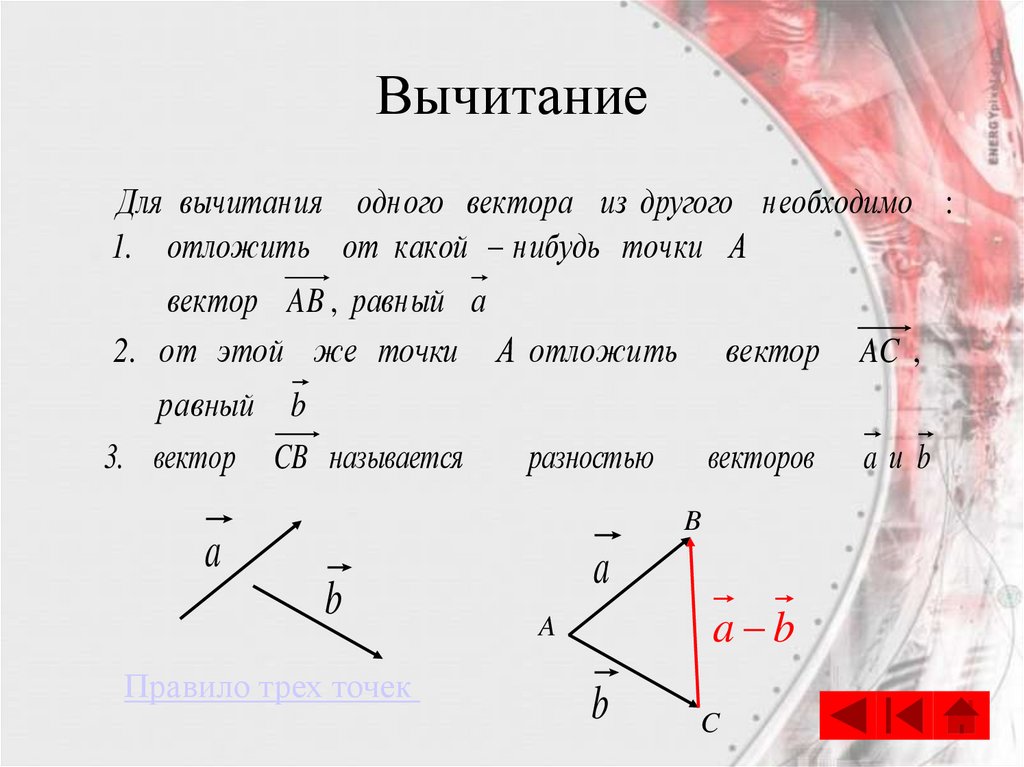
Вычитание
Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB , равный а
2. от этой же точки А отложить
вектор
AC ,
равный b
3. вектор CB называется
векторов
aиb
разностью
B
a
b
Правило трех точек
a
a b
A
b
C

32.

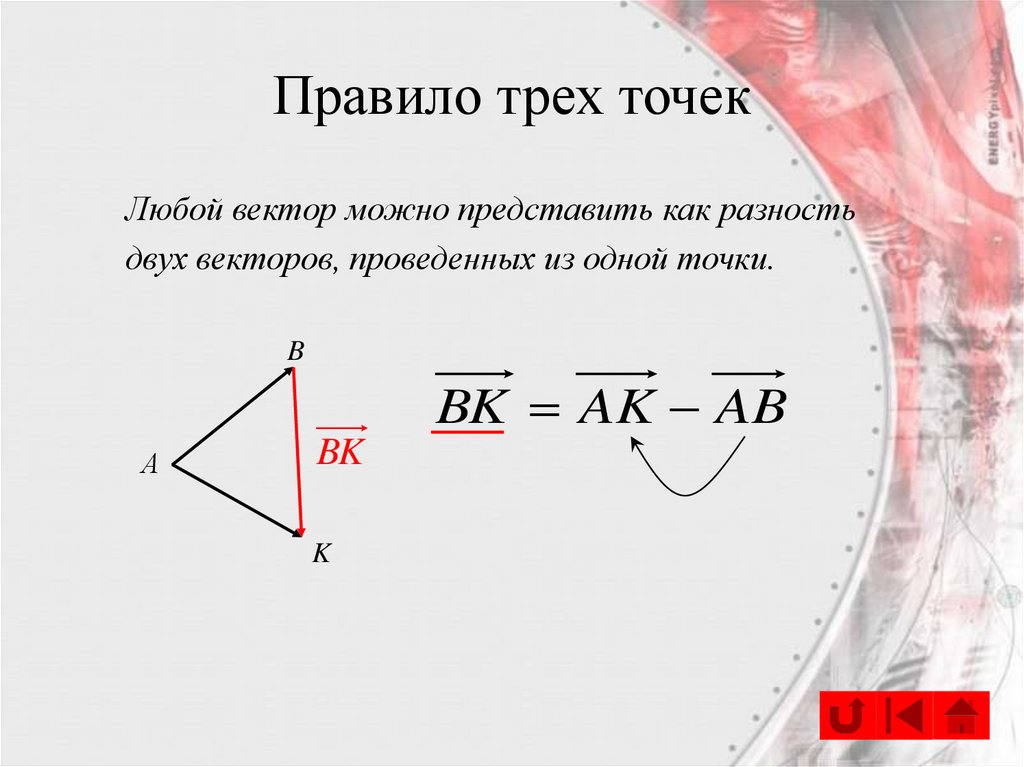
Правило трех точек
Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK AK AB
А
BK
K

33.

Сложение с противоположным
Разность векторов a и b можно представить как
сумму вектора
вектору
.
иaвектора, противоположного
b
a b a b
a
B
b
a b
b
O
А
a

34.

Умножение вектора на число
Произведен
ием ненулевого
вектора
a на число
называется
такой
b , длина
которого
вектор
к а , при чем векторы
равна
при k 0 и противопол
a
ожно
2a
b
a и b сонаправле
направлены
1
b
3
k
ны
при k 0.

35.

Свойства
• Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
• Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

36.

Свойства
Для любых векторов a и b и любых
чисел k, l справедлив ы равенства :
(kl) a k(l a )
сочетатель ный закон
k( a b ) k a k b
1 ый распредели тельный
закон
(k l) a k a l a
2 ой распредели тельный
закон

37.

Скалярное произведение
Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
a b a b cos ( a ; b )
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

38.

Справедливые утверждения
• скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0
a b
• скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
2
a
а
2
а
2

39.

Вычисление скалярного
произведения в координатах
Скалярное произведен ие векторов a x 1 ; y 1 ; z 1
и b x 2 ; y 2 ; z 2 выражается
a b x1 x 2 y1 y2 z1 z2
Доказательство
формулой

40.

Доказательство формулы скалярного
произведения
Доказатель
ство :
I . при a 0 или b 0 , равенство
a b x 1 x 2 y 1 y 2 z 1 z 2 справедлив
о , т .к . 0 0;0;0
II . при a 0 , b 0
О произвольн ая точка
B
b
OA a , OB b
если a и b неколлинеа рны , то
α a
AB 2 OA 2 OB 2 2 OA OB cos α ( по теореме Oкосинусов )
A
это равенство верно и в том случае когда векторы
a и b коллинеарн ы
O
B
A
B
2
2
cos α 1, AB
(OA OB)
2
2
OA OB 2OA OB
2
2
OA OB 2OA OBcos α
2
2
cos α 1, AB
(OA OB)
2
2
OA OB 2OA OB
2
2
OA OB 2OA OBcos α
b
O
a
A

41.

Доказательство формулы скалярного
произведения
Так как AB b a , OA a , OB b , то
2
2
2
1
ab ( a b b a )
2
a x1 ; y 1 ; z 1 b x 2 ; y 2 ; z 2 b a x 2 x1 ; y 2 y 1 ; z 2 z 1
2
2
a x y z , b x 22 y 22 z 22 ,
2
1
2
1
2
1
2
b a (x 2 x1 ) 2 (y 2 y 1 ) 2 (z 2 z 1 ) 2
1 2
(x1 y 12 z 12 x 22 y 22 z 22 (x 2 x1 ) 2 (y 2 y 1 ) 2
2
1
(z 2 z 1 ) 2 ) (x12 y 12 z 12 x 22 y 22 z 22 x 22 2x 1 x 2
2
x12 y 22 2y 1 y 2 y 12 z 22 2z 1 z 2 z 12 ) x1 x 2 y 1 y 2 z 1 z 2
ab

42.

Свойства скалярного
произведения
Для любых
числа
10.
k справедлив
a , b и с и любого
ы равенства
:
2
a 0 причем a 0 при a 0
20. a b b a
30.
векторов
(переместительный закон)
a b c a c b c (распределительный
закон)
(сочетательный закон)
40. k a b k a b

43.

Разложение вектора
• По двум неколлинеарным векторам
• По трем некомпланарным векторам

44.

Разложение вектора по двум
неколлинеарным векторам
Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.
Доказательство

45.

Доказательство теоремы
Дано :
b
a , b неколлинеа рные
векторы
Доказать :
p
a
P
B
a A
1)Пусть p коллинеарен b .
Тогда p y b , где y –
некоторое число.
Следовательно,
p
b
O
p xa yb
Доказатель ство :
A1
p 0 a y b
т.е. p разложен по
векторам a и b .

46.

Доказательство теоремы
2) p не коллинеарен ни вектору a , ни вектору b .
Отметим О – произвольную точку.
OA a OB b OP p
PA BO PA OA A
1
1
1
p OA 1 A1 P (пп правилу треугольни ка)
но : OA 1 и A1 P коллинеарн ы a и b соответств енно,
значит OA 1 x a , A1 P y b ,
следовател ьно p x a y b , т.е. p разложен по a и b
ч.т.д.

47.

Доказательство теоремы
Докажем, что коэффициенты разложения
определяются единственным образом.
Допустим: p x1 a y 1 b
Тогда: p x a y b z c
1
1
-
1
p xa yb zc
0 (x x1 )a (y y 1 )b
x x 1 0, y y 1 0,
если бы x x 1 0 то a
y y1
b
x x1
а значит a , и b коллинеарн ы, что
противореч ит условию теоремы
значит x x1 0, y y 1 0, откуда
x x1 и y y 1 .

48.

Разложение вектора по трем
некомпланарным векторам
Если вектор p представлен в виде
p xa yb zc
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
Доказательство

49.

Доказательство теоремы
С
P
pB
с b P2 P1
O
aA
Доказатель ство :
О произвольн ая точка
Дано :
abc
некомпланрные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP 2 P2 P1 P1 P
OP 2 , и OA , PP 1 и OB , P1 P , OC коллинеарн ы
OP 2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a y b z c ч.т.д.

50.

Доказательство теоремы
Докажем, что коэффициенты разложения
определяются единственным образом.
Допустим: p x1 a y 1 b z 1 c
Тогда: p x a y b z c
1
p x a yb z c
1
-
1
0 (x x1 )a (y y1 )b (z z 1 )c
x x1 0, y y1 0, z z 1 0
x x1
y y1
если бы z z 1 0 то с
a
b
z z1
z z1
а значит a , b , и с компланарны, что
противореч ит условию теоремы
значит x x1 , y y1 , z z 1

51.

Базисные задачи
Вектор, проведенный в середину отрезка
Вектор, проведенный в точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид треугольника
Вектор, проведенный в точку пересечения
диагоналей параллелограмма
Вектор, лежащий на диагонали параллелепипеда

52.

Вектор, проведенный в середину
отрезка,
равен полусумме векторов, проведенных из той же
точки в его концы.
С
A
B
O
1
1
1
OC ( OA OB ) OA OB
2
2
2
Доказательство

53.

Доказательство
С
A
B
O
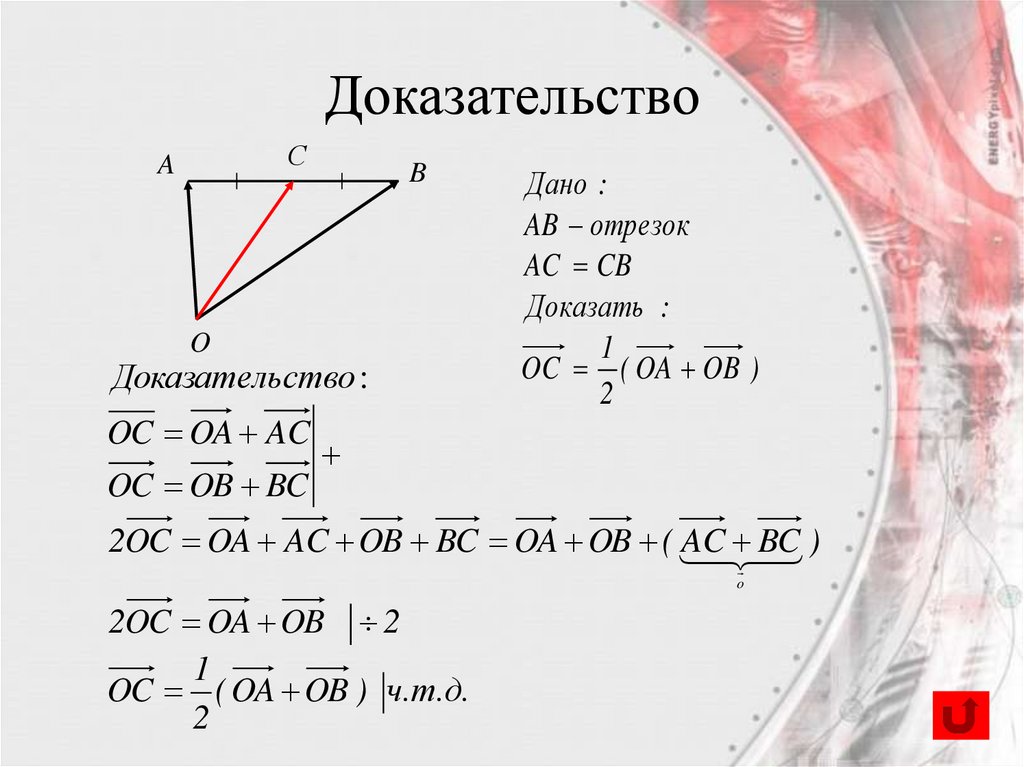
Доказательство :
OC OA AC
OC OB BC
Дано :
AB отрезок
AC CB
Доказать :
1
OC ( OA OB )
2
2OC OA AC OB BC OA OB (
AC
BC
)
o
2OC OA OB 2
1
OC ( OA OB ) ч.т.д.
2

54.

Вектор, проведенный в точку отрезка
Точка С делит отрезок АВ в отношении т : п.
A
m
Сn
B
O
n
m
OC
OA
OB
m n
m n
Доказательство

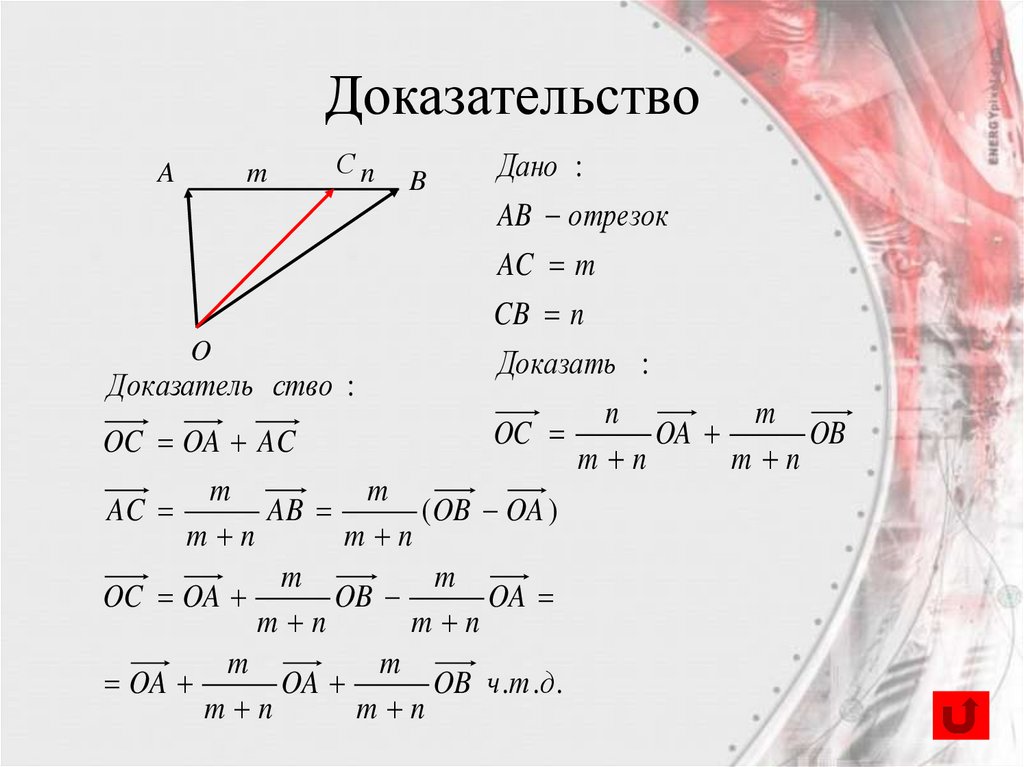
55.

Доказательство
A
m
Сn
O
Доказатель ство :
B
Дано :
AB отрезок
AC m
CB n
Доказать :
n
m
OC
OA
OB
m n
m n
OC OA AC
m
m
AC
AB
( OB OA )
m n
m n
m
m
OC OA
OB
OA
m n
m n
m
m
OA
OA
OB ч .т .д.
m n
m n

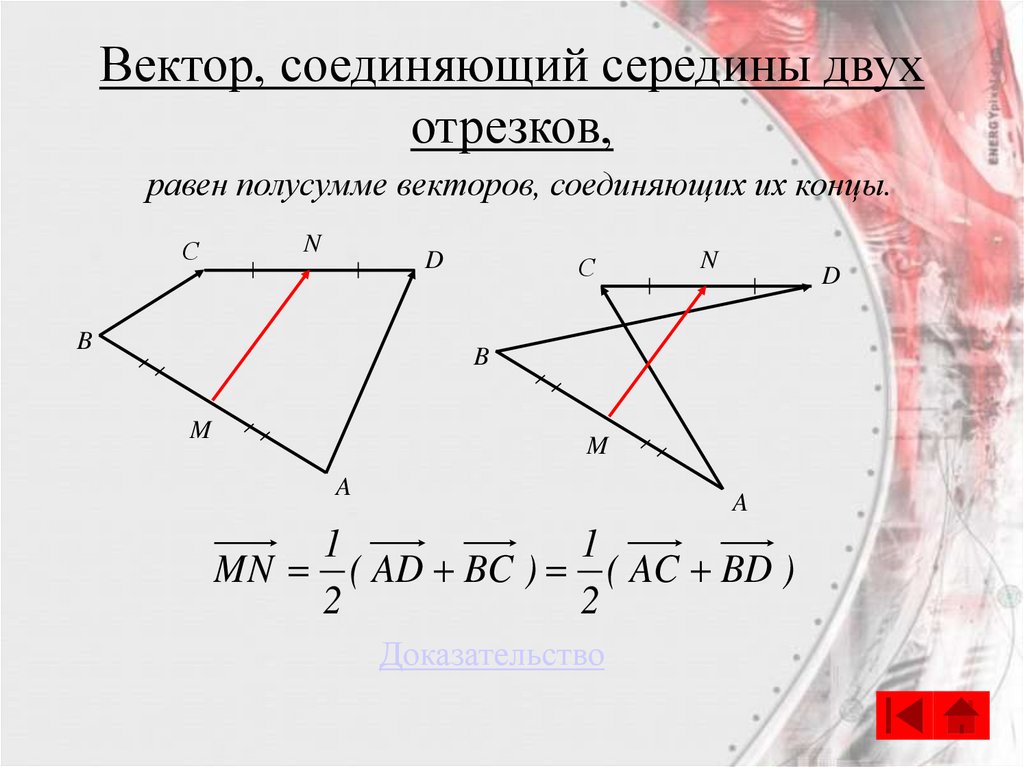
56.

Вектор, соединяющий середины двух
отрезков,
равен полусумме векторов, соединяющих их концы.
С
N
D
B
С
N
D
B
M
M
A
A
1
1
MN ( AD BC ) ( AC BD )
2
2
Доказательство

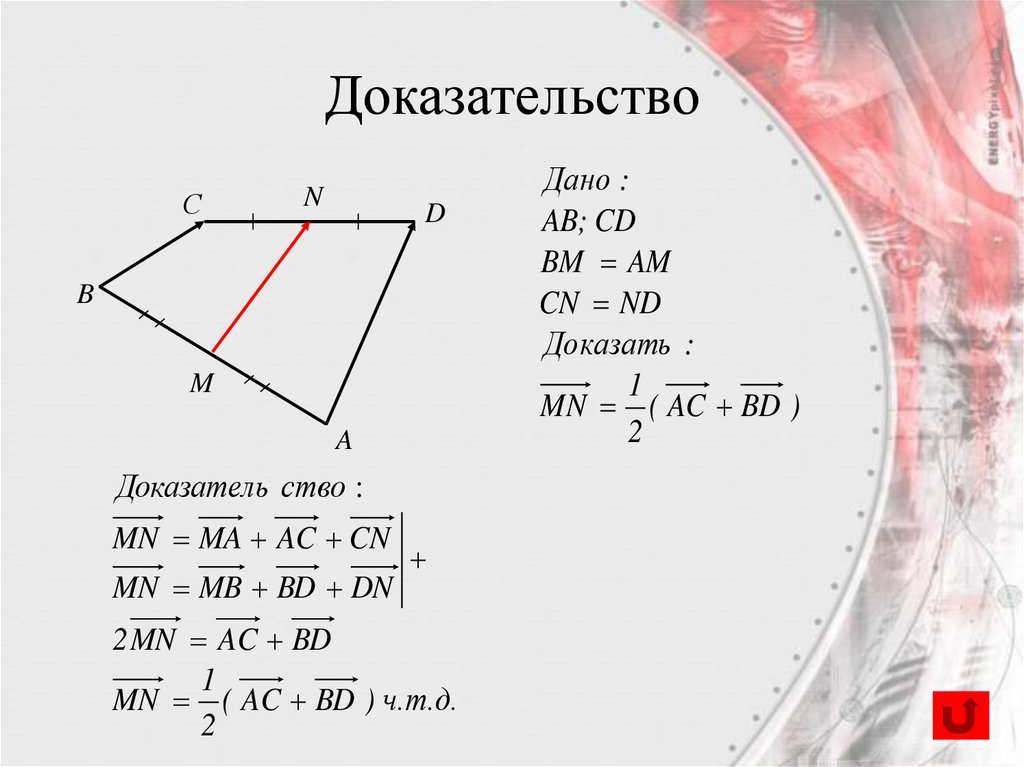
57.

Доказательство
С
N
D
B
M
A
Доказатель ство :
MN MA AC CN
MN MB BD DN
2 MN AC BD
1
MN ( AC BD ) ч.т.д.
2
Дано :
AB; CD
BM AM
CN ND
Доказать :
1
MN ( AC BD )
2

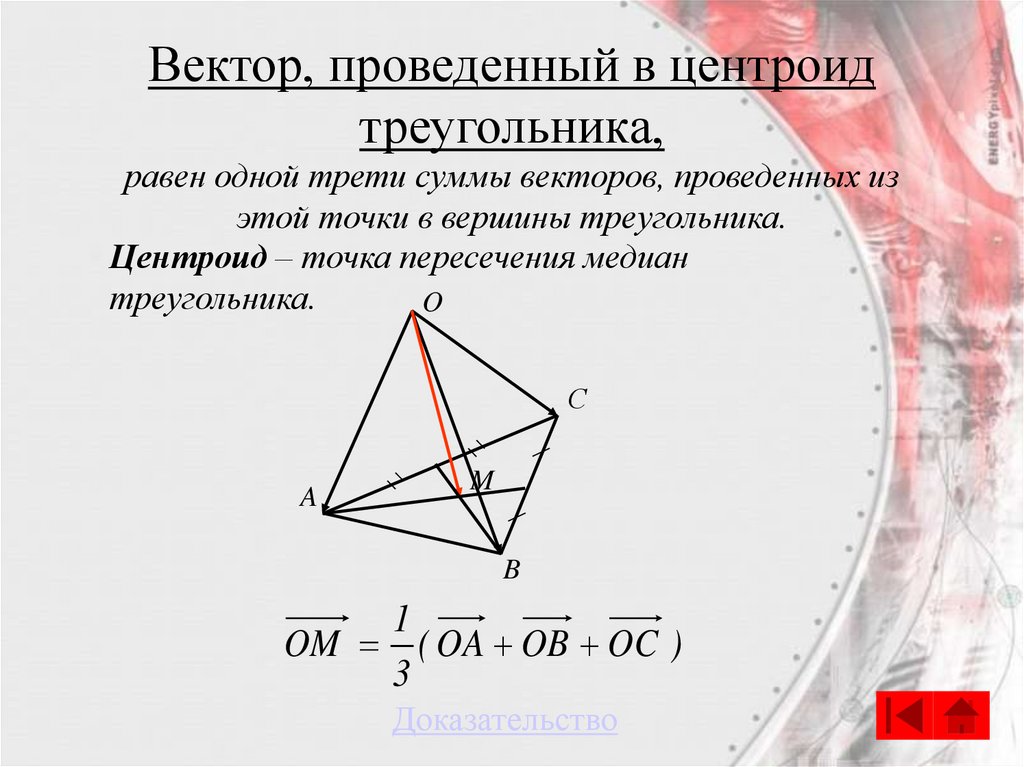
58.

Вектор, проведенный в центроид
треугольника,
равен одной трети суммы векторов, проведенных из
этой точки в вершины треугольника.
Центроид – точка пересечения медиан
треугольника.
O
С
A
M
B
1
OM ( OA OB OC )
3
Доказательство

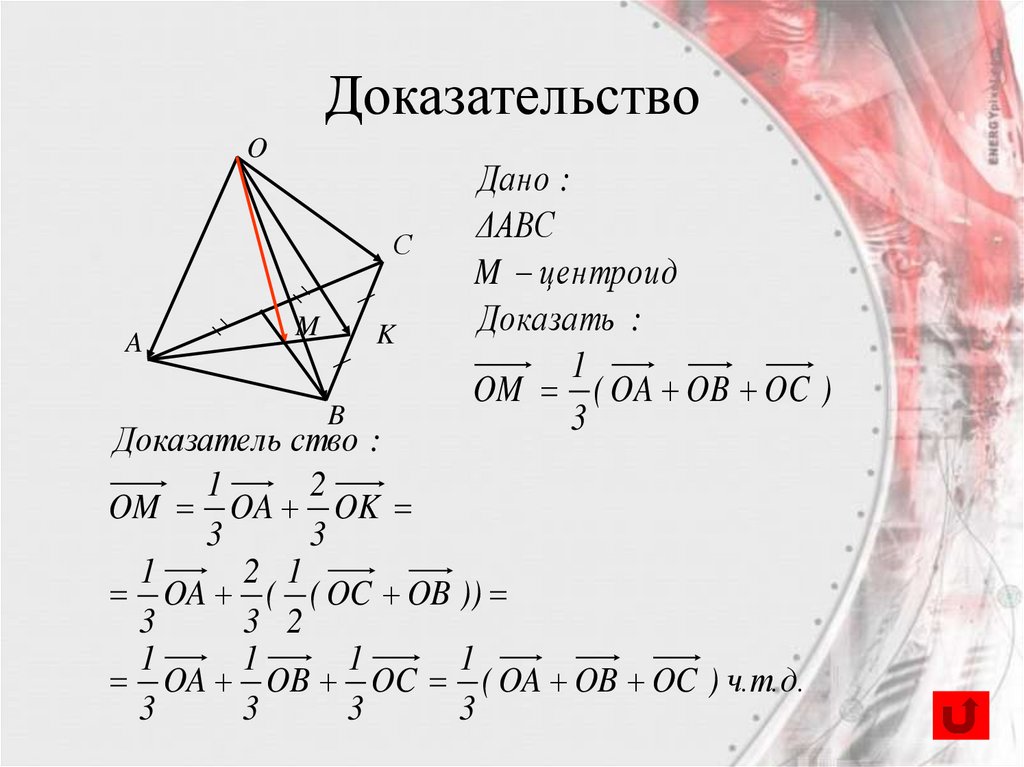
59.

Доказательство
O
С
A
M
K
B
Дано :
ΔABC
M центроид
Доказать :
1
OM ( OA OB OC )
3
Доказатель ство :
1
2
OM OA OK
3
3
1
2 1
OA ( ( OC OB ))
3
3 2
1
1
1
1
OA OB OC ( OA OB OC ) ч.т.д.
3
3
3
3

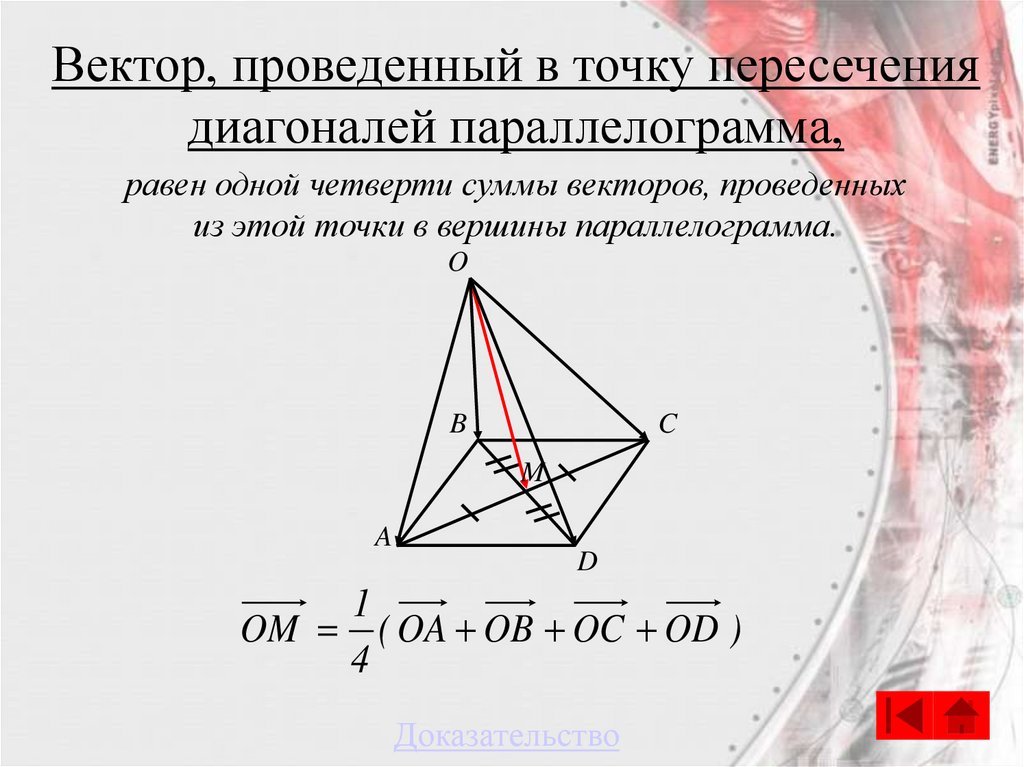
60.

Вектор, проведенный в точку пересечения
диагоналей параллелограмма,
равен одной четверти суммы векторов, проведенных
из этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство

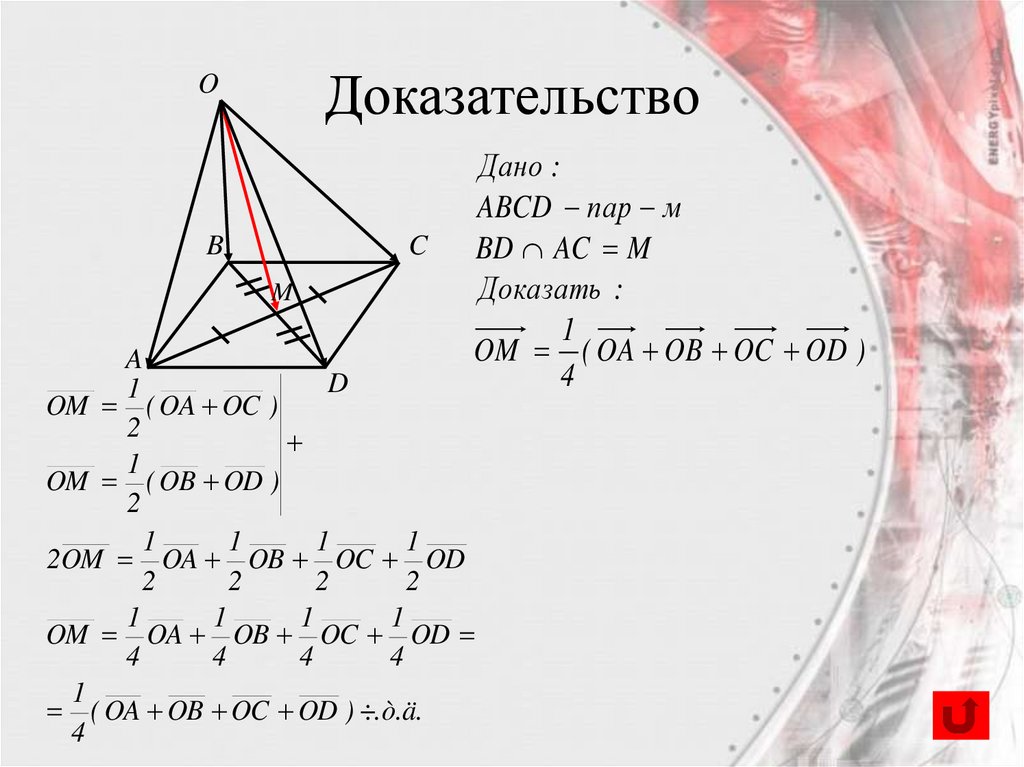
61.

Доказательство
O
B
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷.ò.ä.
4

62.

Вектор, лежащий на диагонали
параллелепипеда,
равен сумме векторов, лежащих на трех его ребрах,
исходящих из одной вершины.
B1
C1
A1
a
A
d
D1
B
C
b
с
D
d a b c
Доказательство

63.

Доказательство
B1
C1
A1
a
A
d
AA 1 a
D1
B
C
b
D
с
Доказатель ство :
AC 1 AA 1 AB 1 BC 1
AA 1 AB AD
a b c ч .т .д .
Дано :
ABCDA 1 B 1 C 1 D 1 пар м
AB b
AD c
AC 1 d
Доказать
:
d a b c

64.

Помощь в управлении
презентацией
• управление презентацией осуществляется с
помощью левой клавиши мыши
• переход от одного слайда к другому и на
гиперссылки по одиночному щелчку
• завершение презентации при нажатии кнопки
выход
переход к следующему слайду
возврат к содержанию
возврат к подтеме
возврат с гиперссылок

65.

Проверь себя
• Устные вопросы
• Задача 1. Задача на доказательство
• Задача 2. Разложение векторов
• Задача 3. Сложение и вычитание векторов
• Задача 4. Скалярное произведение

66.

Устные вопросы
Справедливо ли утверждение:
а) любые два противоположно направленных
вектора коллинеарны?
б) любые два коллинеарных вектора сонаправлены?
в) любые два равных вектора коллинеарны?
г) любые два сонаправленных вектора равны?
д) если a b , b c , то a c ?
е) существуют векторы a , b и c такие, что a
и c не коллинеарны, b и c не коллинеарны, а a
и b коллинеарны?
Ответы

67.

Ответы
а) ДА
б) НЕТ (могут быть и противоположно
направленными)
в) ДА
г) НЕТ (могут иметь разную длину)
д) ДА
е) ДА

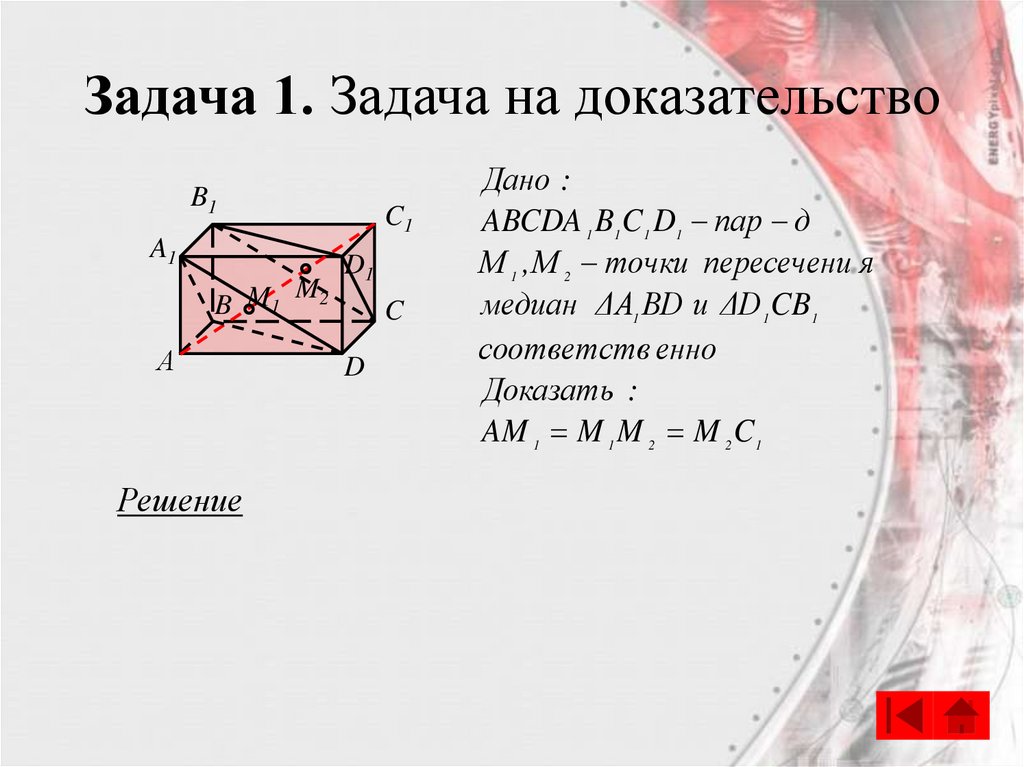
68.

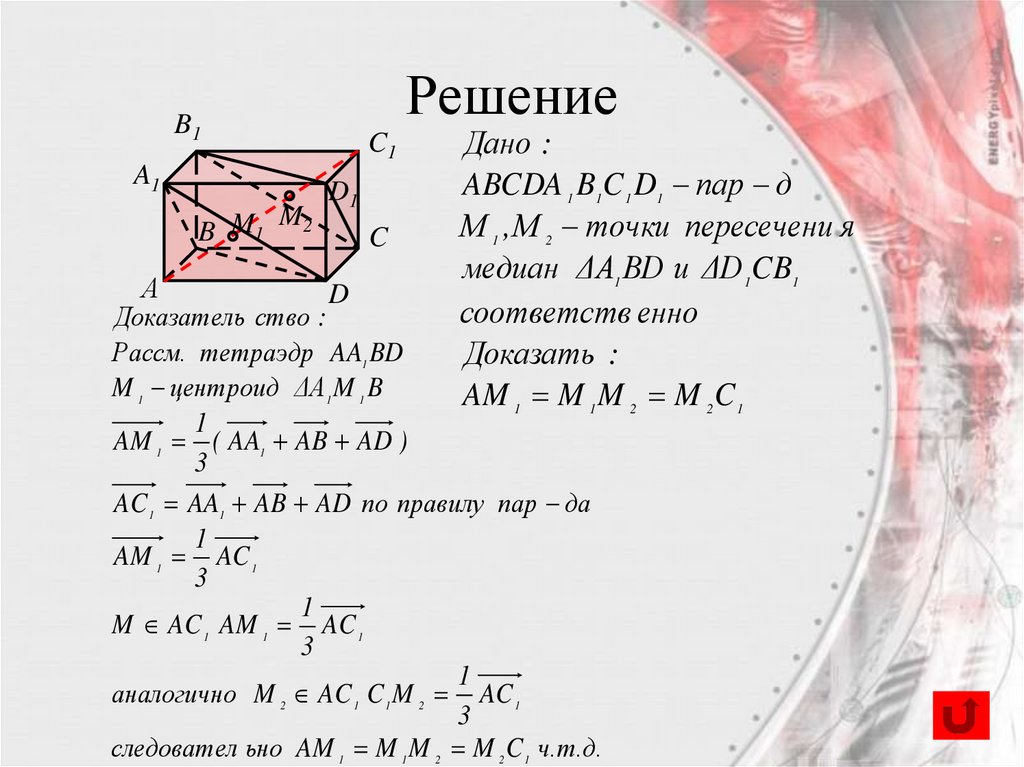
Задача 1. Задача на доказательство
B1
C1
A1
B M1
А
Решение
M2
D1
C
D
Дано :
ABCDA 1 B1C 1 D1 пар д
М 1 , М 2 точки пересечени я
медиан ΔА1 ВD и ΔD 1CB1
соответств енно
Доказать :
AM 1 M 1 M 2 M 2 C 1

69.

Решение
B1
C1
A1
B M1
M2
D1
C
Дано :
ABCDA 1 B1C 1 D1 пар д
М 1 , М 2 точки пересечени я
медиан ΔА1 ВD и ΔD 1CB1
соответств енно
Доказать :
AM 1 M 1 M 2 M 2 C 1
А
D
Доказатель ство :
Рассм. тетраэдр AA1 BD
M 1 центроид ΔA1 M 1 B
1
AM 1 ( AA1 AB AD )
3
AC 1 AA1 AB AD по правилу пар да
1
AM 1 AC 1
3
1
M AC 1 AM 1 AC 1
3
1
аналогично M 2 AC 1 C 1 M 2 AC 1
3
следовател ьно AM 1 M 1 M 2 M 2 C 1 ч.т.д.

70.

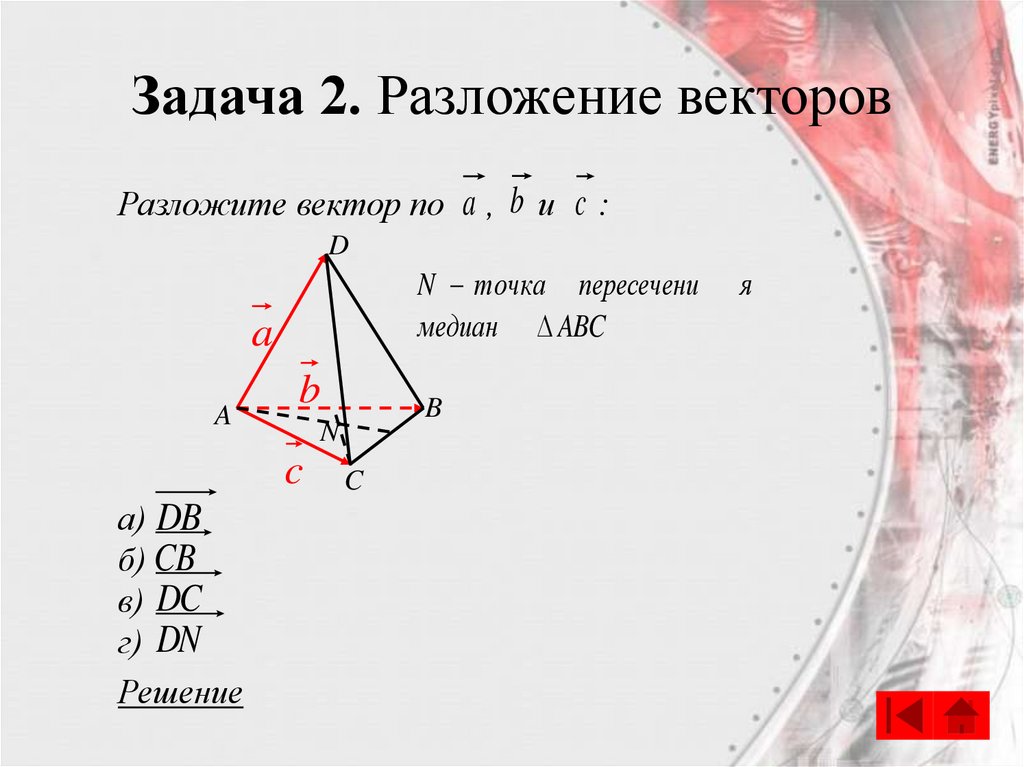
Задача 2. Разложение векторов
Разложите вектор по a , b и c :
D
N точка пересечени
медиан ABC
a
A
b
N
c
а) DB
б) CB
в) DC
г) DN
Решение
B
C
я

71.

Решение
а) DB b a
б) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2

72.

Задача 3. Сложение и вычитание
Упростите выражения:
а) CM MK
б) DM MA
в) SD ST
г) PL PK
д) AC BC PM AP BM
е) AD MP EK EP MD
Решение

73.

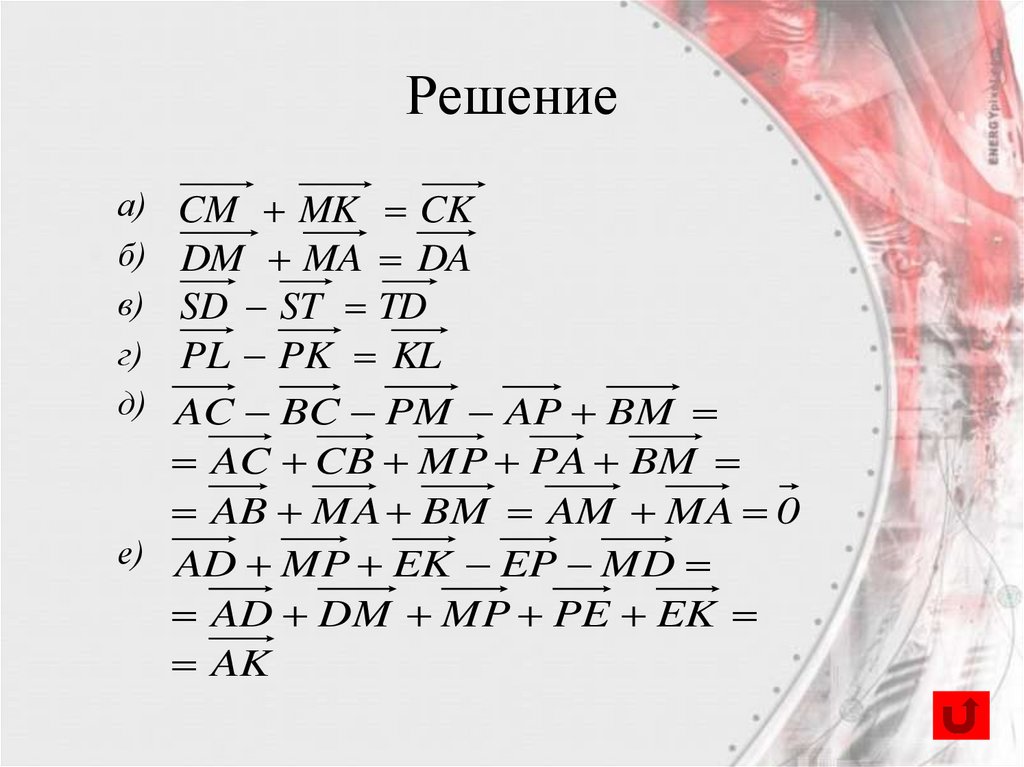
Решение
CM MK CK
DM MA DA
SD ST TD
PL PK KL
AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK
а)
б)
в)
г)
д)

74.

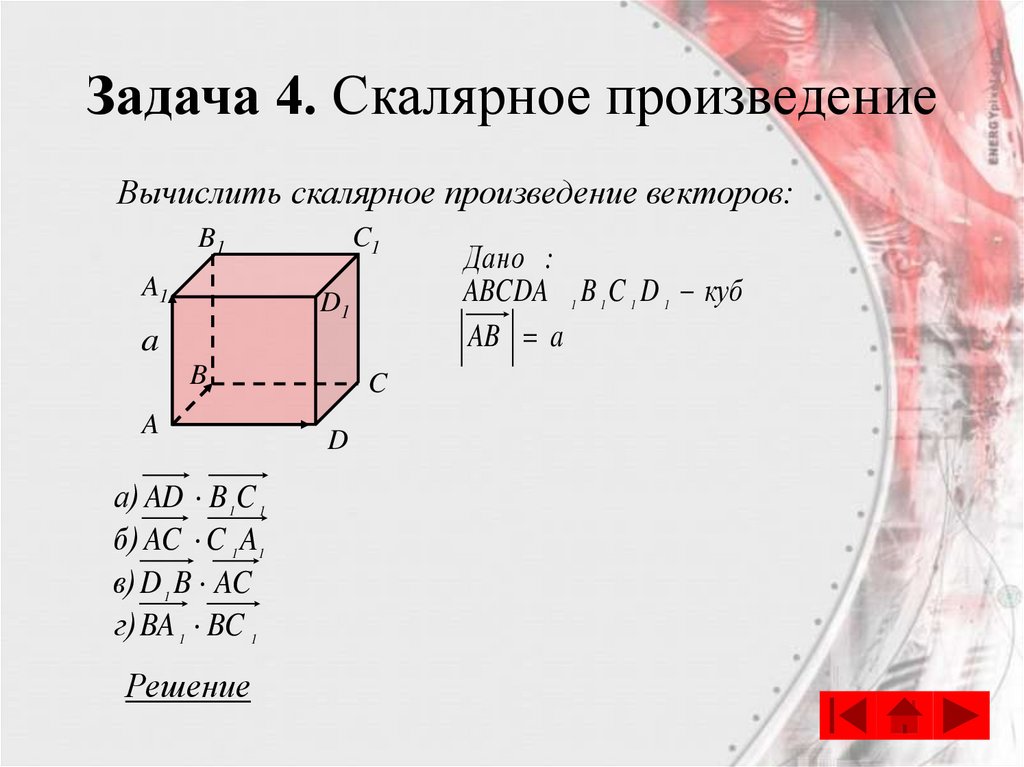
Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов:
C1
B1
A1
D1
a
B
A
а) AD B 1 C 1
б) AC C 1 A1
в) D 1 B AC
г) BA 1 BC 1
Решение
C
D
Дано :
ABCDA 1 B 1 C 1 D 1 куб
AB a

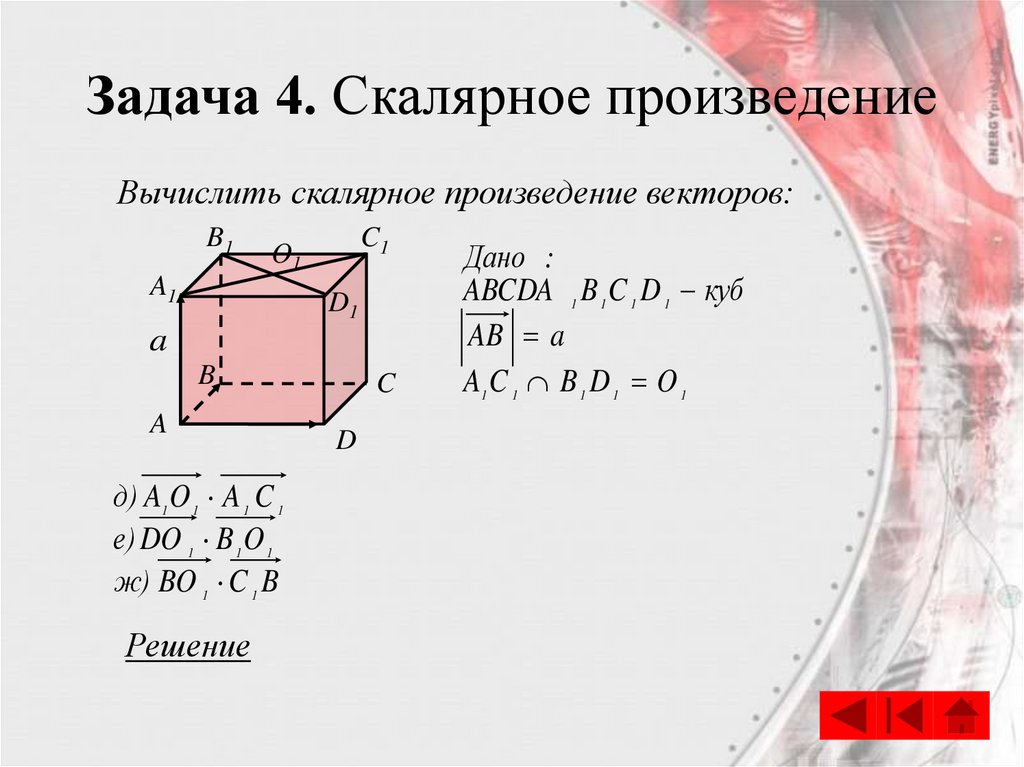
75.

Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов:
B1
C1
O1
A1
D1
a
B
A
д) A1 O 1 A 1 C 1
е) DO 1 B 1 O 1
ж) BO 1 C 1 B
Решение
C
D
Дано :
ABCDA 1 B 1 C 1 D 1 куб
AB a
A1 C 1 B 1 D 1 O 1

76.

Решение
2
а)AD B1C1 AD AD2 a 2
б)AC диагональквадрата
AC A1C1 C1 A1
AC C 1A1 AC ( A1C1 ) AC A1C1 (a 2 )2 2a2
в)D1 B диагональкуба
D1 B a 2 (a 2 )2 3a(п( т.Пифагораиз ΔDD1 B)
2
D1 B AC 3a 2 a 2 cos45 a3 6
a3 3
2
г)BA1 , BC1 диагоналиквадратов
ΔA1 BC1 равносторонний, A1 BC1 60
1 2a2
BA1 BC1 a 2 a 2
a2
2
2

77.

Решение
д)A1O1 половинадиагоналиквадрата
A1C1 диагональ квадрата
O1 A1C1 0
a 2
A1O1 A1 C1
a 2 cos0 a 2
2
е)D1O1 , B1O1 половиныдиагонали квадрата
a 2 a 2
a2
D1O1 B1O1 D1O1 ( O1 B1 )
2
2
2

78.

Решение
ж)I способ решениепо определению : B1
C1
O1
a 2 2 a 6
A1
BO1 a 2 (
)
D1
2
2
C1 B диагональквадрата
c
B
1
1
C
b a
O1 BC1 A1 BC1 60 30
2
2
A
a 6
3 2 D
BO1 C1 B BO1 ( BC1 )
a 2 cos30 a
2
2
II способ разложениепо базису:
1
1
BO1 a b c
2
2
C1 B b a
2
1
1
BO1 C1 B ( a b c ) ( a b ) ( a ab
2
2
2
1
1
1
1 2
1 2
3
ac bc ab b ) ( a a ) a 2
2
2
2
2
2
2