Similar presentations:
Автоматизоване керування стрічковим конвеєром з розробкою підсистеми адаптивного керування тепловими режимами роботи
1.
Міністерство освіти і науки УкраїниКриворізький національний університет
Факультет інформаційних технологій
Кафедра автоматизації, комп’ютерних наук і технологій
КВАЛІФІКАЦІЙНА РОБОТА
на здобуття ступеню вищої освіти – магістр
за освітньо-професійною програмою
«Кіберфізичні системи в промисловості, бізнесі та транспорті»
зі спеціальності
174 – Автоматизація, комп’ютерно-інтегровані технології та робототехніка
тема роботи:
«Автоматизоване керування стрічковим конвеєром з розробкою
підсистеми адаптивного керування тепловими режимами роботи
приводного барабана»
Виконав ст. гр. АКІТР-23-2м.
Керівник
___________ Єфименко М.С.
___________Курганов І.Д.
2.
Об'єктом досліджень є технологічний процес транспортування рудноїмаси стрічковими конвеєрами.
Предмет дослідження – методи оптимального управління натягом
стрічки та швидкістю обертання приводного барабана стрічкового
конвеєра із застосуванням інтегрального критерію якості управління
тепловими втратами
Ідея роботи полягає в автоматичному керуванні натягом стрічки або її
швидкістю на основі інформації зосередженої в теплових втратах для
контролю та оптимального керування режимами роботи фрикційної пари
приводний барабан – стрічка конвеєра.
Метою роботи є створення адаптивних підсистем автоматичного
управління натяжною та приводною станціями конвеєрних установок з
контролем кута робочого ковзання, що забезпечують раціональні режими
роботи конвеєра.
3. Задачі для вирішення відповідно поставленої мети
• 1. Розробити модель для визначення величини кутаробочого ковзання, в зоні якого відбувається випромінювання
теплового джерела внаслідок дії сил тертя.
• 2. Виконати цифрове моделювання теплового поля
фрикційної пари, засобами пакета MATLAB у додатку PDE
Toolbox методом кінцевих елементів.
• 3. Розробити структурну схему адаптивної системи з
еталонною моделлю, як систему з розподіленими
параметрами, що дозволяє реалізувати результати цифрового
моделювання двовимірного розподілу теплового поля
фрикційної пари барабан-стрічка.
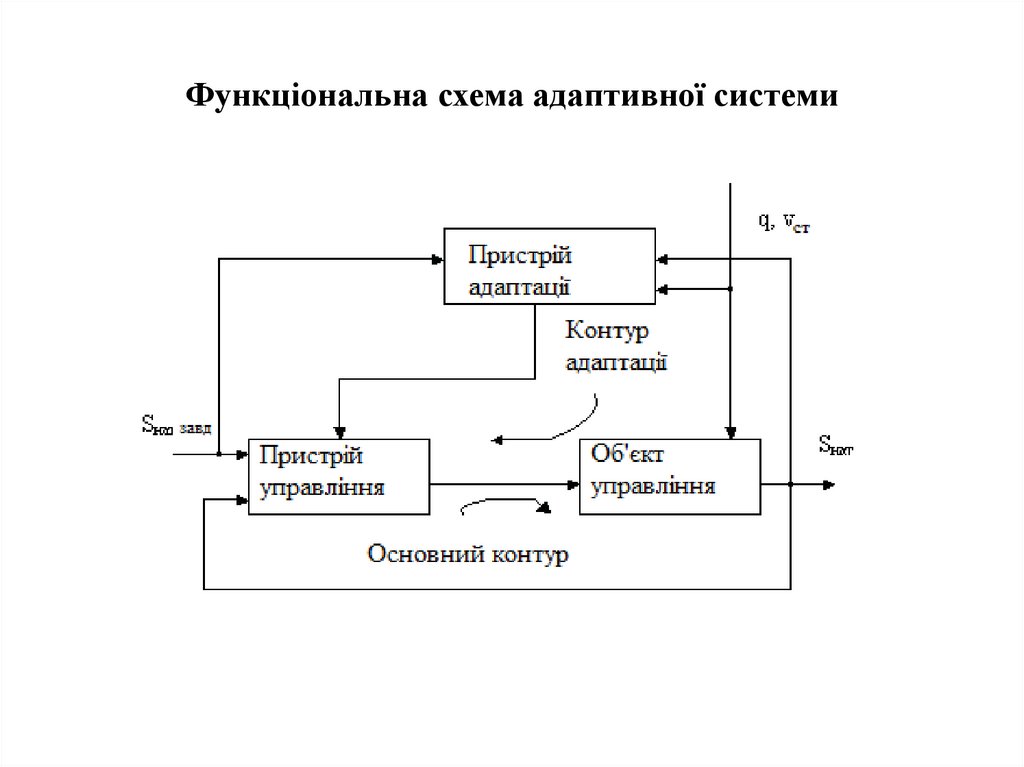
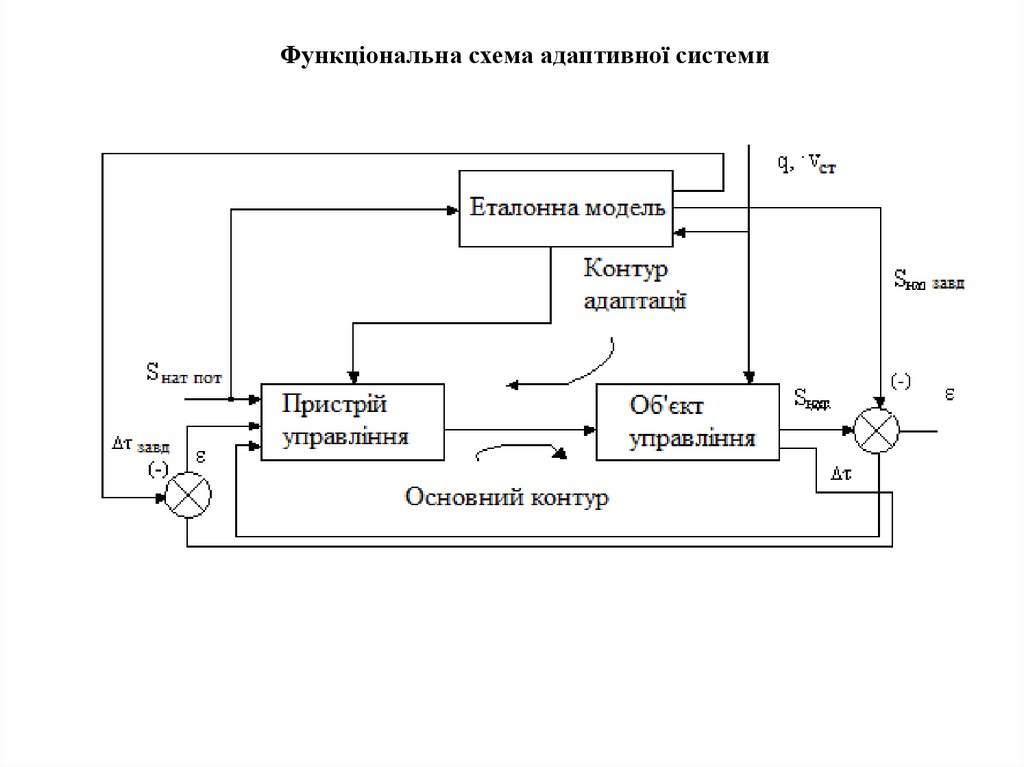
4. Функціональна схема адаптивної системи
5.
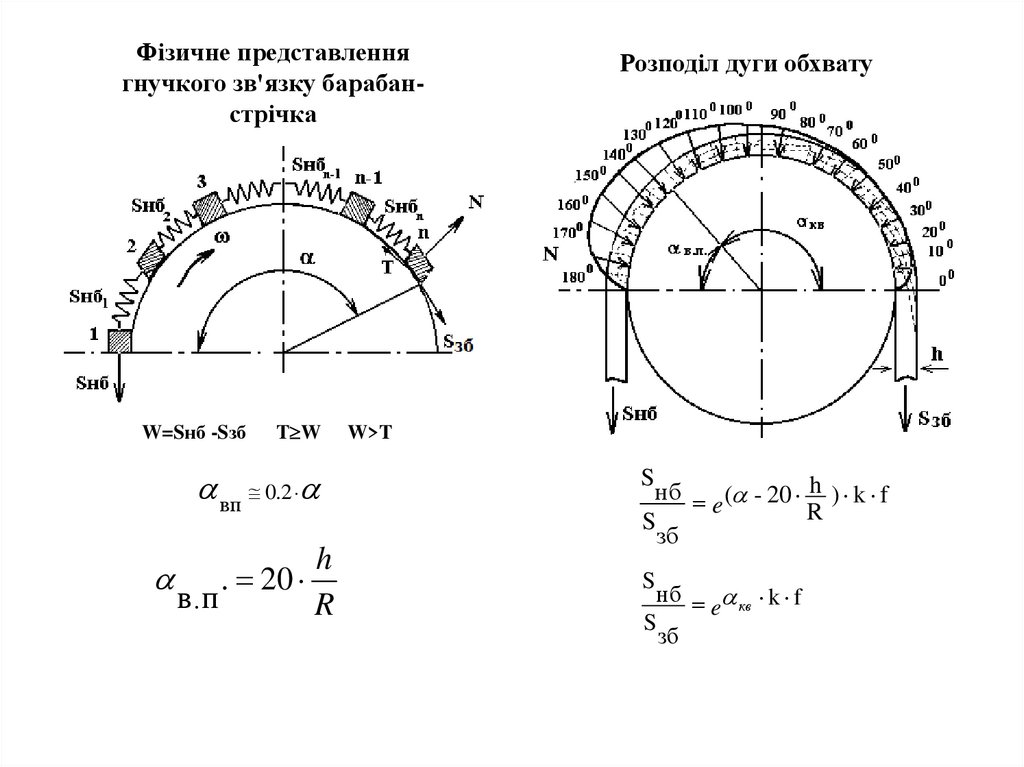
Фізичне представленнягнучкого зв'язку барабанстрічка
W=Sнб -Sзб
T W
Розподіл дуги обхвату
W>T
вп 0.2
S
h
. 20
в.п
R
S
нб ( - 20 h ) k f
e
R
S
зб
нб кв k f
e
S
зб
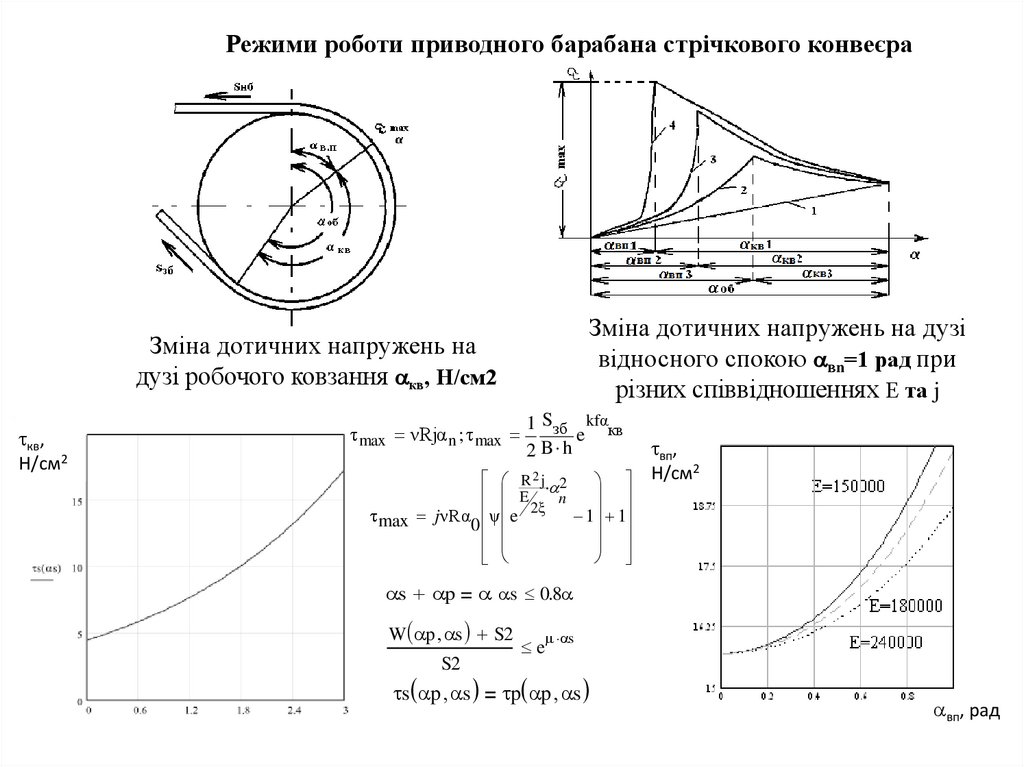
6. Режими роботи приводного барабана стрічкового конвеєра
Зміна дотичних напружень на дузівідносного спокою вn=1 рад при
різних співвідношеннях Е та j
Зміна дотичних напружень на
дузі робочого ковзання кв, Н/см2
кв,
Н/см2
τ max νRjα n ; τ max
1 Sзб kfαкв
e
2 B h
вп,
2
Н/см
R 2 j 2
n
E
2ξ
τ max jνRα0 ψ e
1 1
s p
s 0.8
W p s S2
S2
s p s
e
s
p p s
вп, рад
7.
Математична модель з розподіленими параметрамиx1
x1
t x1
1( x, t ) N 0 ( x, , t ) 1 ( )d N1 ( x, , t ) 1 ( )d G ( x, , t , ) f ( , , u ( , )) d d
0
0
1
0
x0
x0
t
t
0
0
0 x0
K 0 ( x, t , ) g 0 ( , u 0 ( )) d K1 ( x, t , ) g1 ( , u1 ( )) d ,
10(0)(x) = 10(1)(x)=0 x [x0, x1] g0(t, u0(t))= g1(t, u1(t))=0, t>0
f ( x, t , u ( x, t )) ( x 0 ) (t 0 )
t x1
1( x, t ) G ( x, , t , ) ( 0 ) ( 0 )d d G ( x, 0 , t , 0 )
0 x0
t x1
1( x, t ) G ( x, , t ) w( , )d d
0 x0
w , A1 ( ) 1(00) ( ) ( w1 ( , ) w0 ( , )) f ( , , u ( , ))
8.
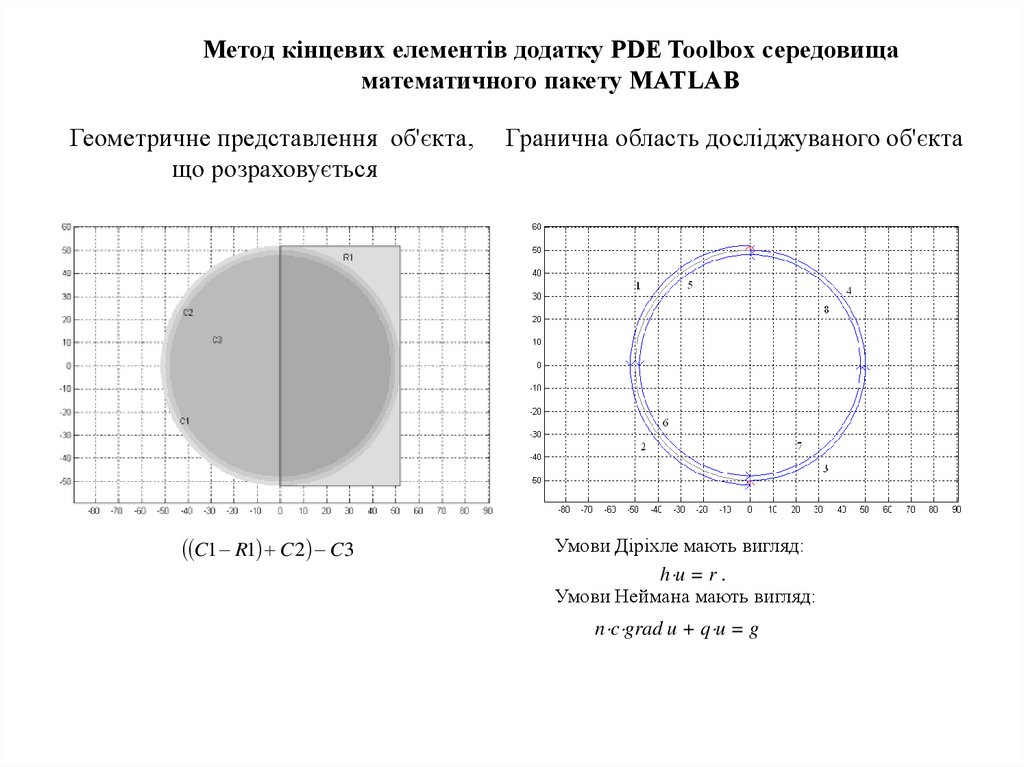
Метод кінцевих елементів додатку PDE Toolbox середовищаматематичного пакету MATLAB
Геометричне представлення об'єкта,
що розраховується
C1 R1 C 2 C3
Гранична область досліджуваного об'єкта
Умови Діріхле мають вигляд:
h u = r .
Умови Неймана мають вигляд:
n c grad u + q u = g
9.
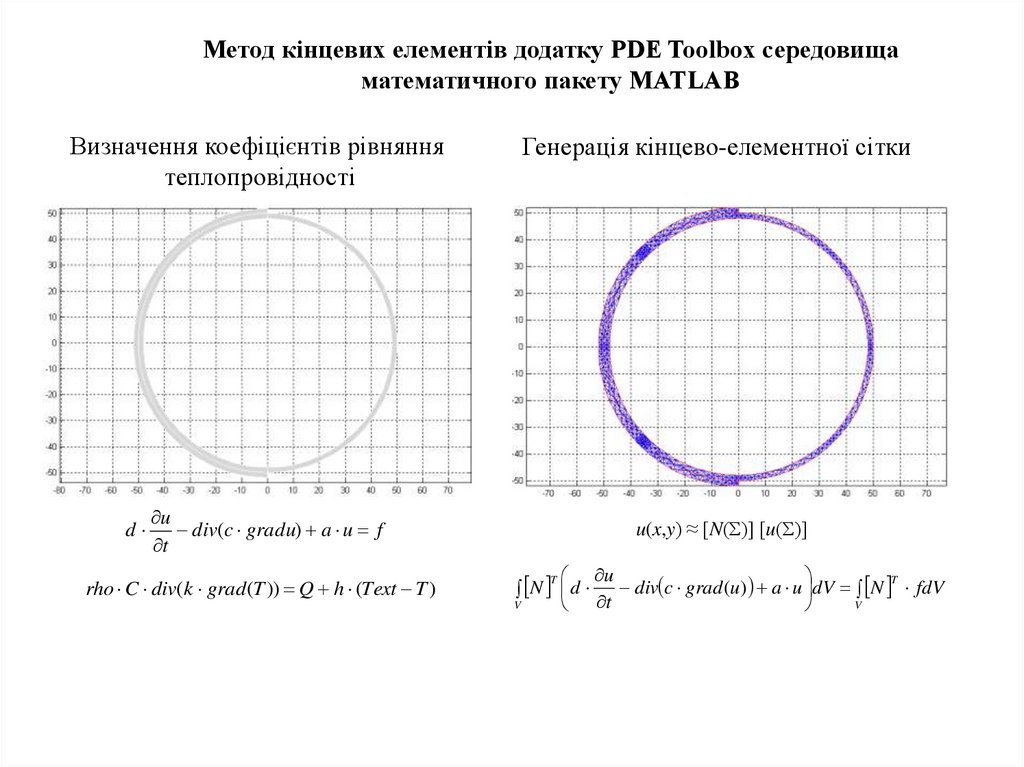
Метод кінцевих елементів додатку PDE Toolbox середовищаматематичного пакету MATLAB
Визначення коефіцієнтів рівняння
теплопровідності
Генерація кінцево-елементної сітки
u
div(c gradu) a u f
t
u(x,y) ≈ [N(Σ)] [u(Σ)]
rho C div(k grad (T )) Q h (Text T )
u
T
T
div c grad (u ) a u dV N fdV
N d
V
V
t
d
10.
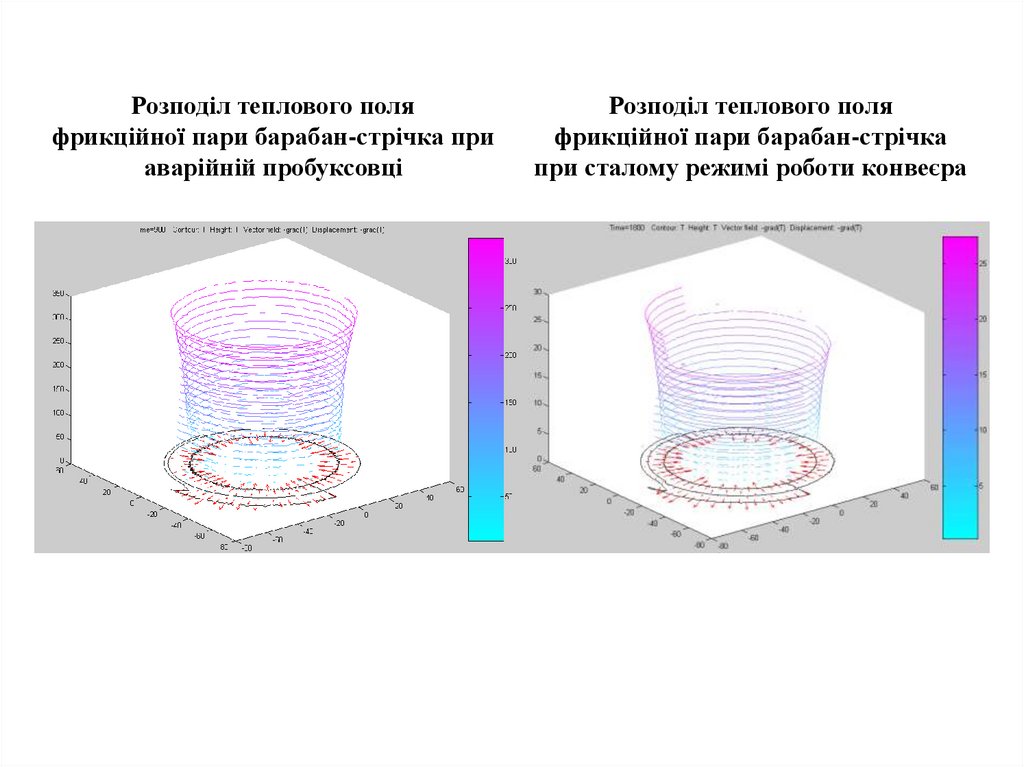
Розподіл теплового поляфрикційної пари барабан-стрічка при
аварійній пробуксовці
Розподіл теплового поля
фрикційної пари барабан-стрічка
при сталому режимі роботи конвеєра
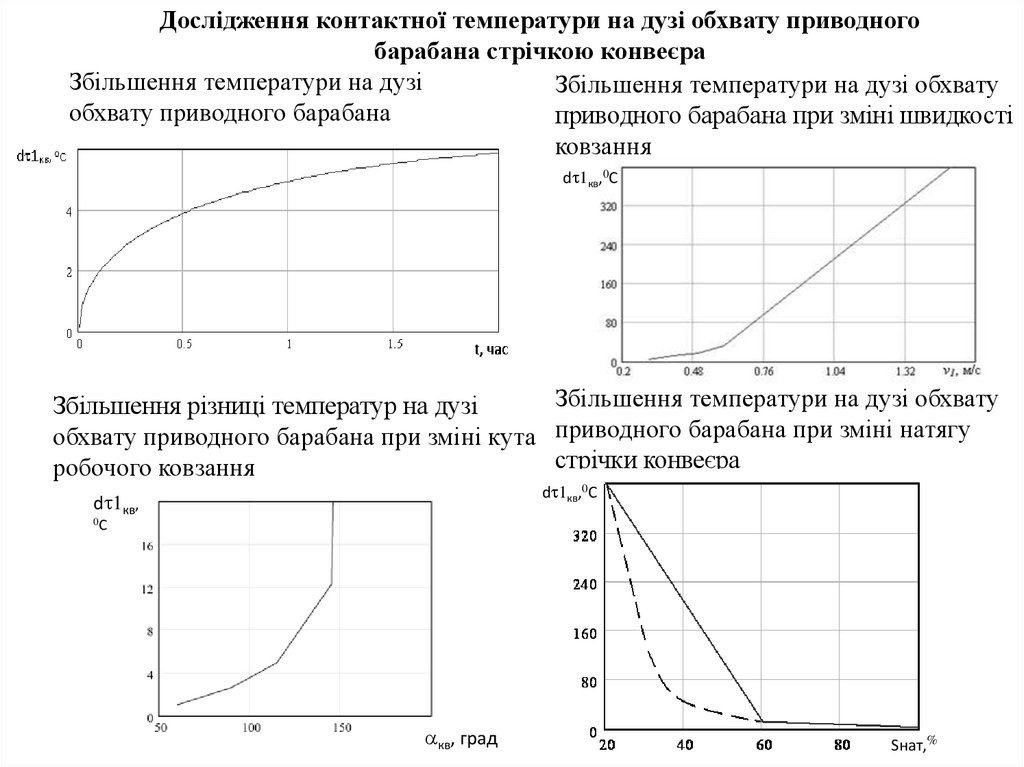
11. Дослідження контактної температури на дузі обхвату приводного барабана стрічкою конвеєра
Збільшення температури на дузіЗбільшення температури на дузі обхвату
обхвату приводного барабана
приводного барабана при зміні швидкості
ковзання
d 1кв,0C
Збільшення температури на дузі обхвату
Збільшення різниці температур на дузі
обхвату приводного барабана при зміні кута приводного барабана при зміні натягу
стрічки конвеєра
робочого ковзання
d 1кв,0C
d 1кв,
0C
кв, град
Sнат,%
12.
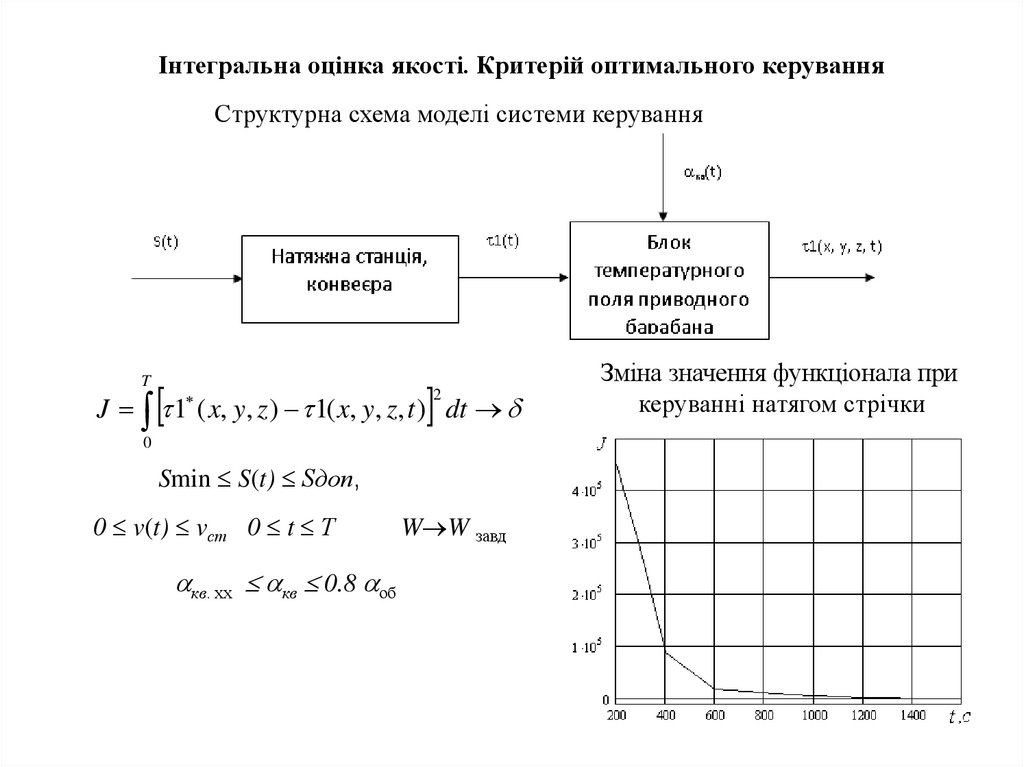
Інтегральна оцінка якості. Критерій оптимального керуванняСтруктурна схема моделі системи керування
T
J 1 ( x, y, z ) 1( x, y, z, t ) dt
2
0
Smin S(t) Sдоп,
0 v(t) vст 0 t Т
кв. хх кв 0.8 об
W W завд
Зміна значення функціонала при
керуванні натягом стрічки
13.
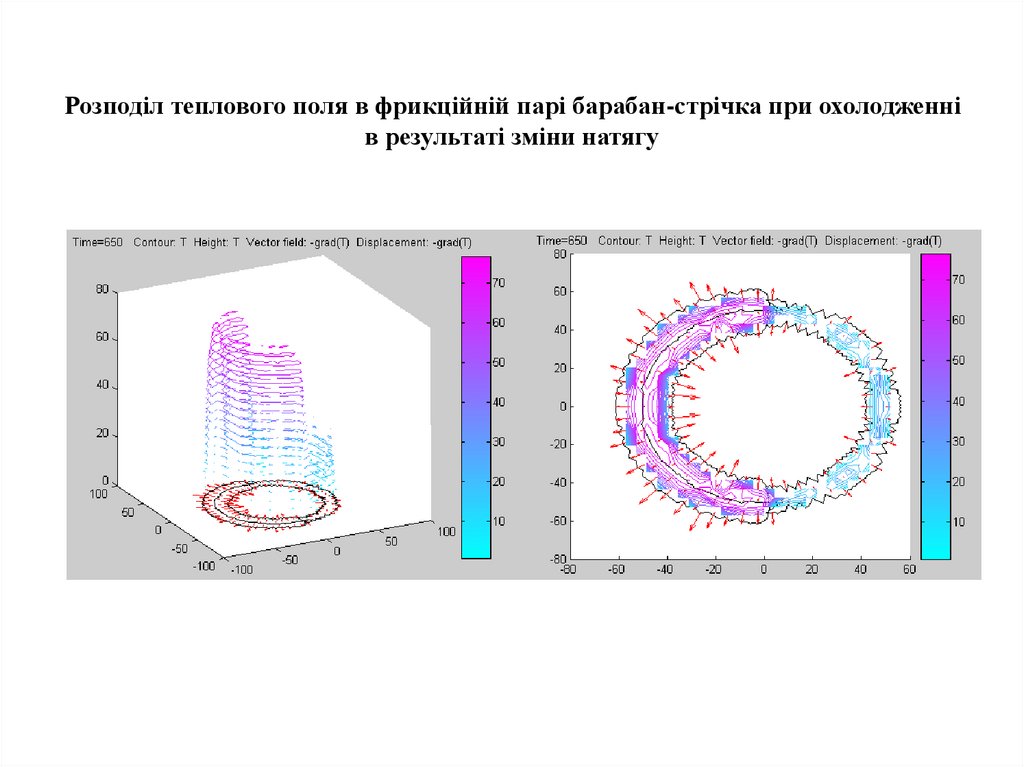
Розподіл теплового поля в фрикційній парі барабан-стрічка при охолодженнів результаті зміни натягу
14.
Функціональна схема адаптивної системи15.
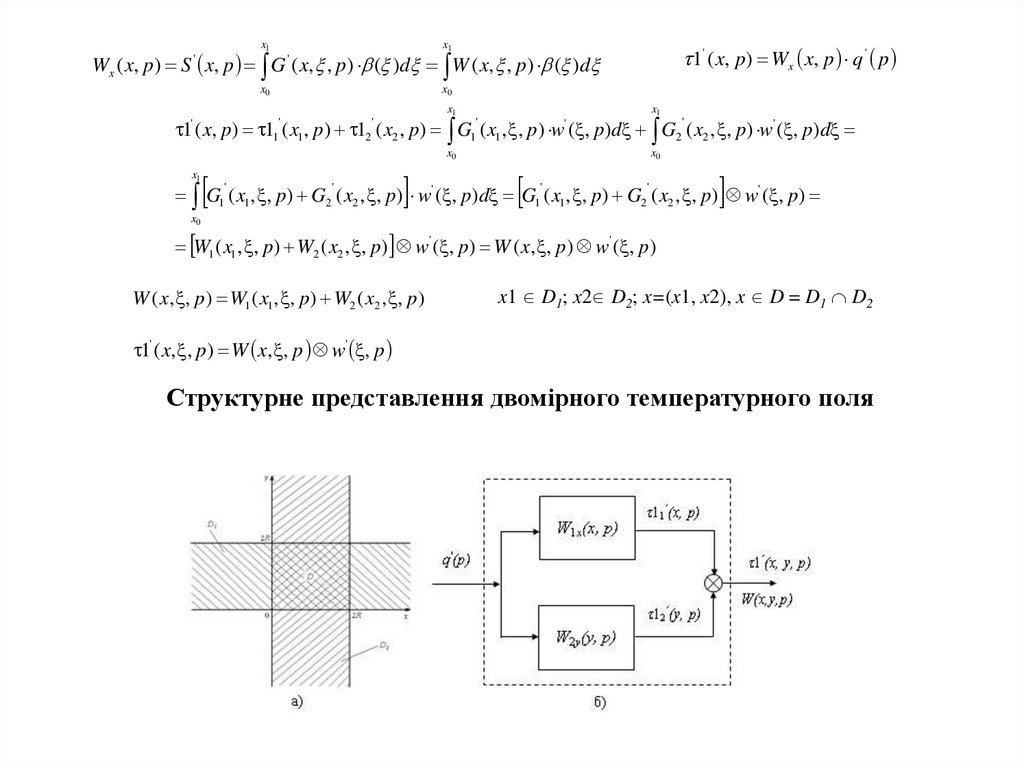
Структурне представлення лінійного об'єкта керування:а – стаціонарний розподілений блок;
б – стаціонарний об'єкт з зосередженими параметрами
t
x1
1( x, t ) G( x, , t ) ( ) q( )d d G( x, , t ) ( )d q( )d S x, t q( )d
0 x0
0
0
x0
t x1
t
Структурне представлення розподіленого x-блока з зосередженим входом та
розподіленим виходом
x1
S x, t G( x, , t ) ( )d
x0
x1
t x1
x1 t
Lt ( 1( x, t )) 1 ( x, p) Lt G( x, , t ) w( , )d d Lt G( x, , t ) w( , )d d G ' ( x, , p) w' ( , p)d
0 x0
x0 0
x0
.
'
де 1’(x, р), G’(x, ,p) и w’( , p) – відповідно зображення виходу об'єкта 1(x, t),
функція Гріна G(x, ,t) і функція керуючого впливу w( , ), а p – комплексна змінна
перетворення Лапласа.
W(x, ,p) = G’(x, ,p)
x1
x1
1 ( x , p ) G ( x , , p ) w ( , p )d q ( p ) G' ( x , , p ) ( )d S ' x , p q' ( p )
'
'
x0
'
'
x0
16.
x11' ( x, p) Wx x, p q ' p
x1
Wx ( x, p) S x, p G ( x, , p) ( )d W ( x, , p) ( )d
'
'
x0
x0
x1
x1
1 ( x, p) 1 ( x1 , p) 12 ( x2 , p) G ( x1 , , p) w ( , p)d G2 ( x2 , , p) w' ( , p)d
'
1
'
'
'
1
'
'
x0
x1
x0
G1 ( x1 , , p) G2 ( x2 , , p) w' ( , p)d G1 ( x1 , , p) G2 ( x2 , , p) w' ( , p)
'
'
'
'
x0
W1 ( x1 , , p) W2 ( x2 , , p) w' ( , p) W ( x, , p) w' ( , p)
W ( x, , p) W1 ( x1 , , p) W2 ( x2 , , p)
x1 D1; x2 D2; x=(x1, x2), x D = D1 D2
1' ( x, , p) W x, , p w' , p
Структурне представлення двомірного температурного поля
17.
d 2 1( x, y, t ) d 2 1( x, y, t )d 1( x, y, t )
dt
dx 2
dy 2
d 1( x, t )
d 2 1( x, t )
2
dt
dx
2
d 1( y, t ) d 1( y, t )
dy2
dt
1( x, y, t ) 11 ( x, t ) 12 ( y, t )
W ( x, y, p) W1x ( x, p) W2 y ( y, p)
x D1; y D2; D = D1 D2
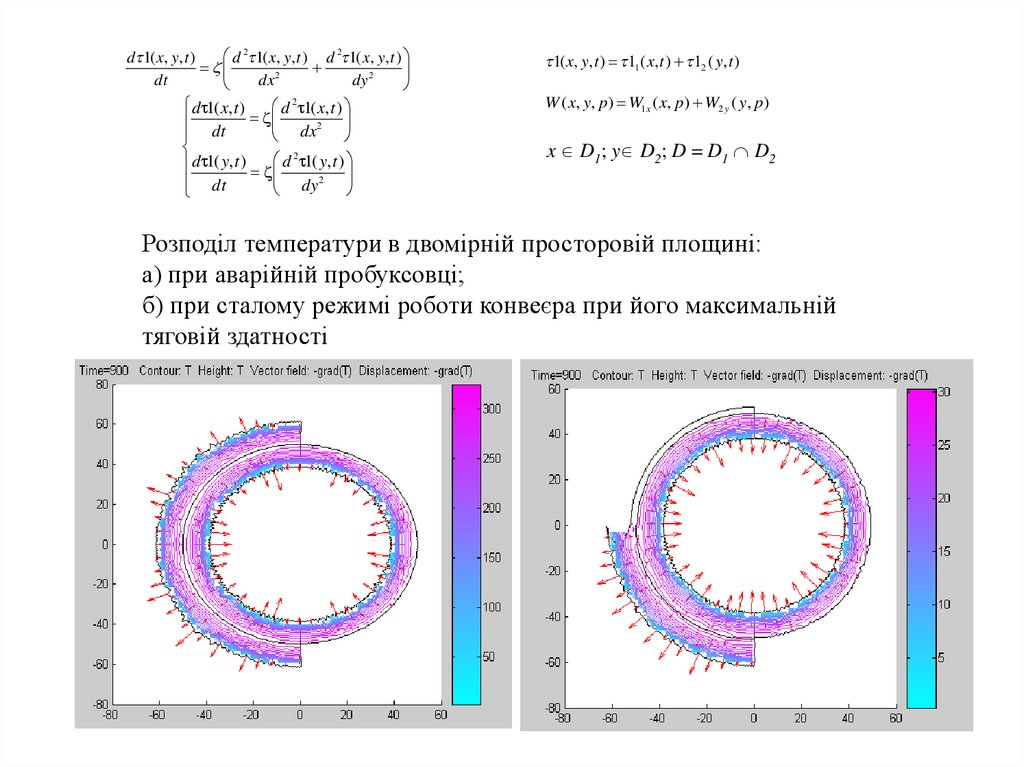
Розподіл температури в двомірній просторовій площині:
а) при аварійній пробуксовці;
б) при сталому режимі роботи конвеєра при його максимальній
тяговій здатності
18. Основні результати:
• Розроблено математичну модель для визначення величиникута робочого ковзання, в зоні якого відбувається
випромінювання теплового джерела внаслідок дії сил
тертя.
• Виконано цифрове моделювання температурного поля
фрикційної пари барабан-стрічка, що дозволяє її
використати в еталонній моделі адаптивної системи
управління.
• Створено адаптивну систему управління, яка дозволяє
мінімізувати
знос
стрічки
та
підвищити
енергоефективність конвеєра.
19.
Практична цінністьЗапропонована система може бути впроваджена на
промислових підприємствах для підвищення надійності
роботи конвеєрних установок і зменшення витрат на
обслуговування.
Висновки
Розроблена система автоматичного керування забезпечує
оптимальний режим роботи стрічкового конвеєра,
підвищуючи його довговічність та ефективність.
Дякую за увагу!







 industry
industry








