Similar presentations:
Операции над векторами. Сложение и вычитание векторов
1.
Операции над векторами.Сложение и вычитание
векторов, умножение
вектора на число
2.
=+
3.
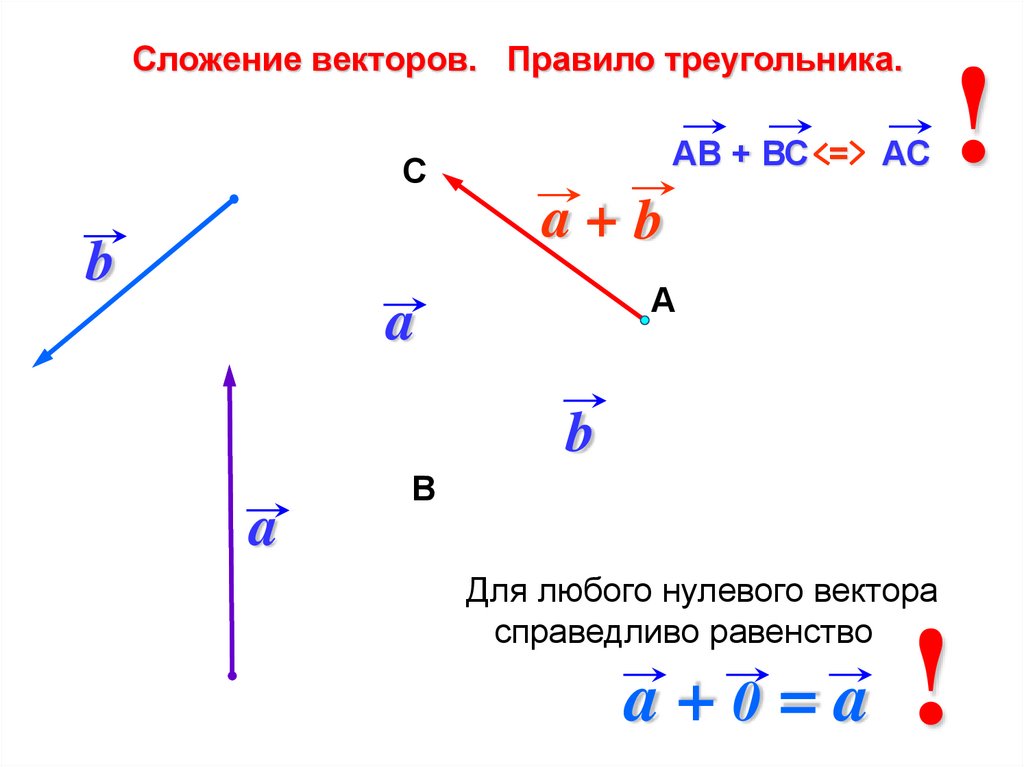
Сложение векторов. Правило треугольника.АВ + ВС = АС
С
!
a+b
b
А
a
b
a
В
Для любого нулевого вектора
справедливо равенство
a+0=a
!
4.
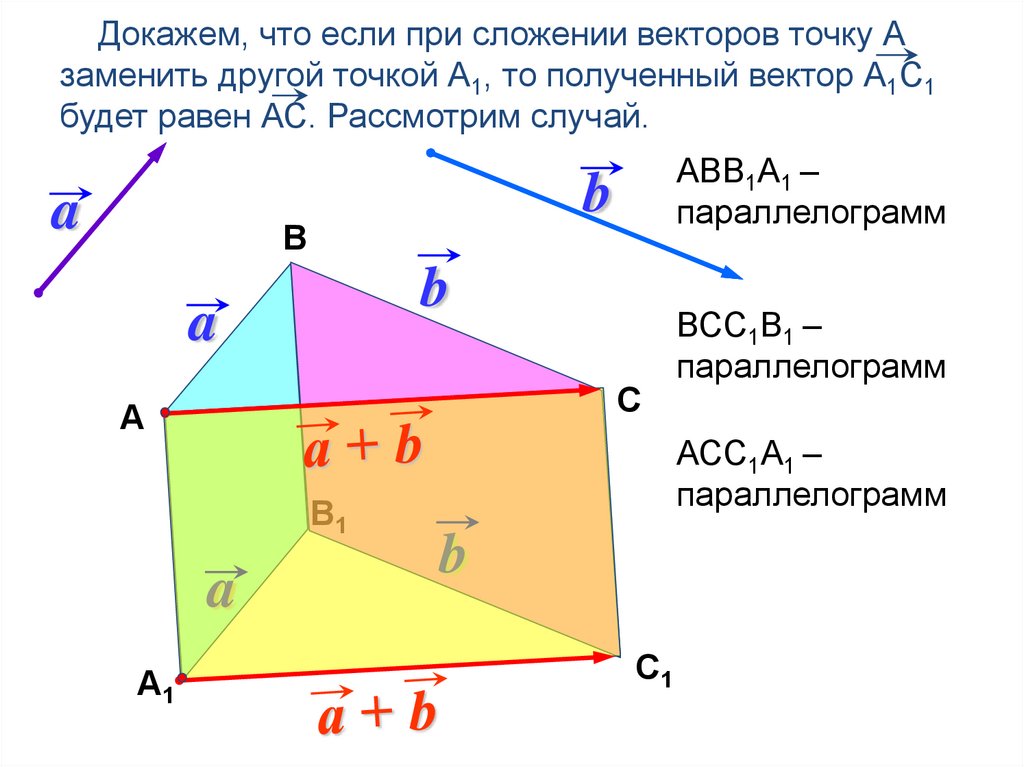
Докажем, что если при сложении векторов точку Азаменить другой точкой А1, то полученный вектор А1С1
будет равен АС. Рассмотрим случай.
a
b
В
b
a
С
А
В1
a
А1
АВВ1А1 –
параллелограмм
ВСС1В1 –
параллелограмм
АСС1А1 –
параллелограмм
b
С1
5.
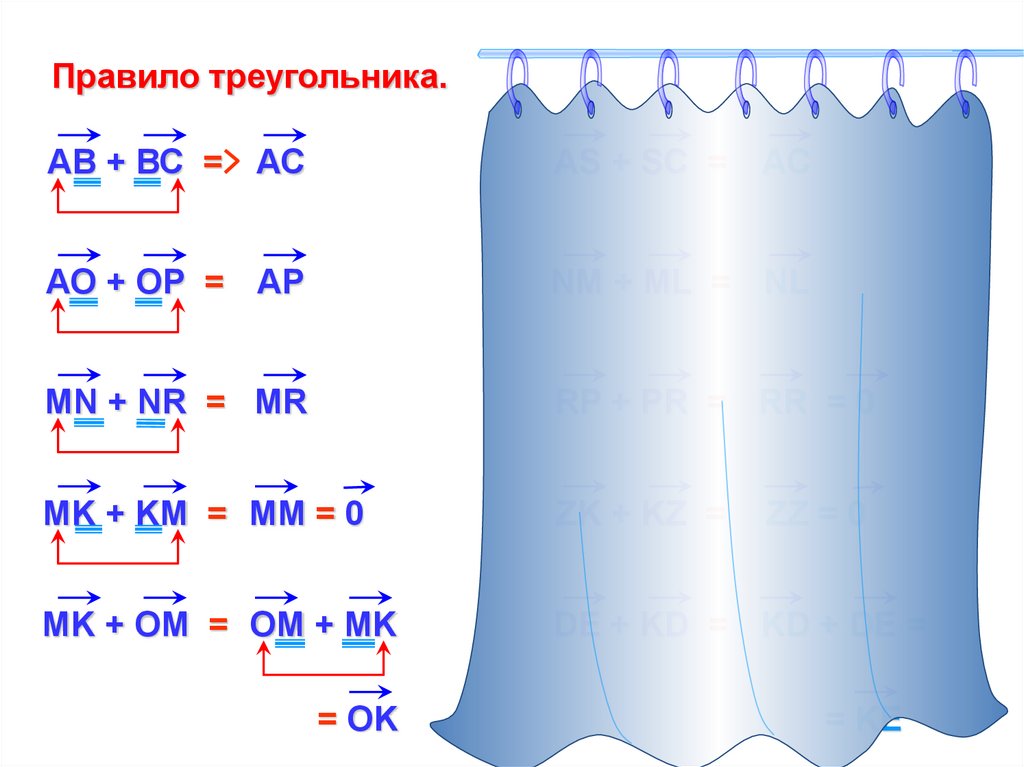
Правило треугольника.АВ + ВС = АС
АS + SС =
АО + ОР = АР
NM + ML = NL
MN + NR = MR
RP + PR = RR = 0
MK + KM = MM = 0
ZK + KZ =
MK + OM = OM + MK
DE + KD = KD + DE =
= OK
АС
ZZ = 0
= KE
6.
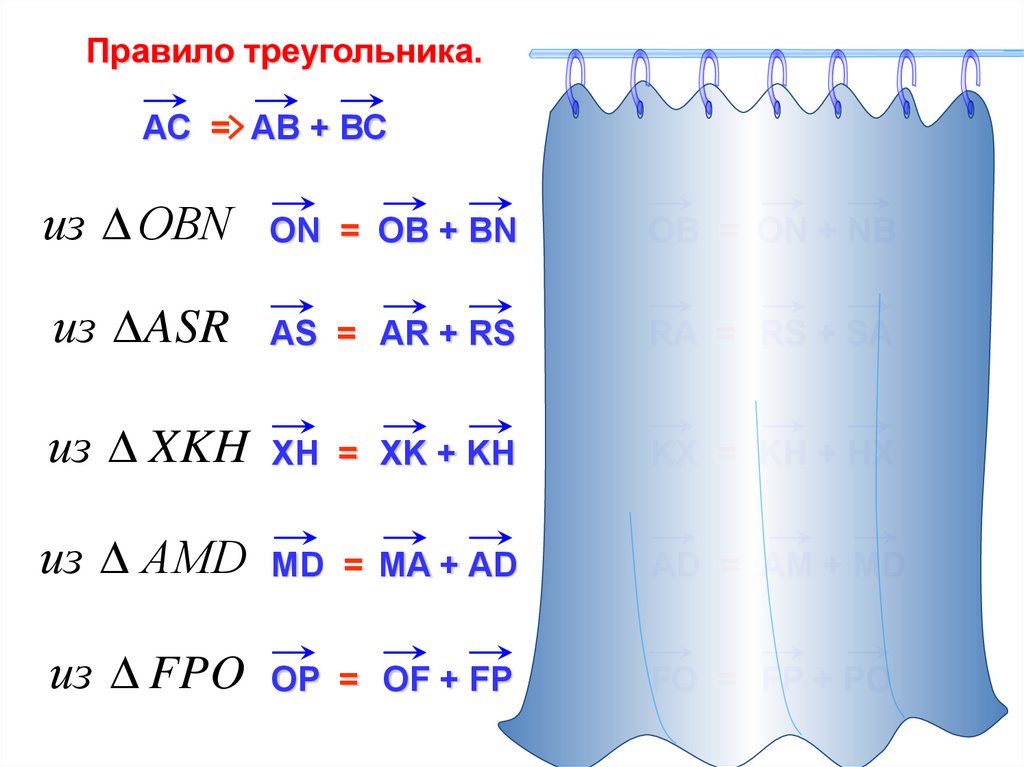
Правило треугольника.АС = АВ + ВС
из ОВN
ON = OB + ВN
OB = ON + NВ
из ASR
AS = AR + RS
RA = RS + SA
из XKH XH = XK + KH
KX = KH + HX
из АMD MD = MA + AD
AD = AM + MD
из FPO OP = OF + FP
FO = FP + PO
7.
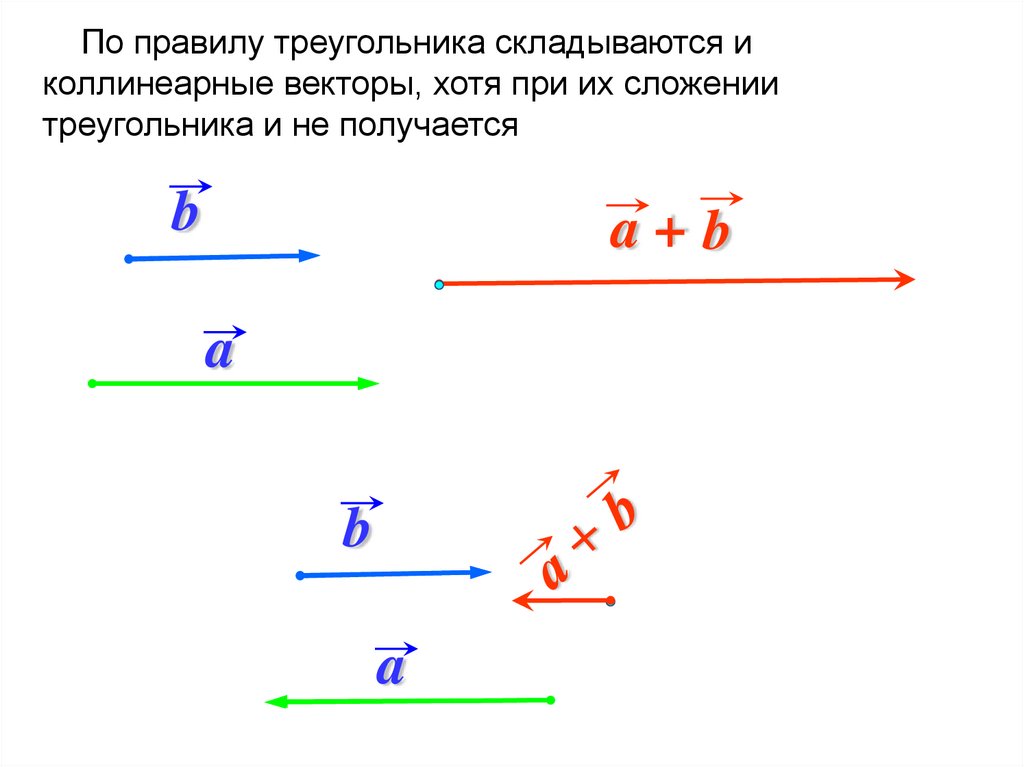
По правилу треугольника складываются иколлинеарные векторы, хотя при их сложении
треугольника и не получается
b
a+b
a
b
a
8.
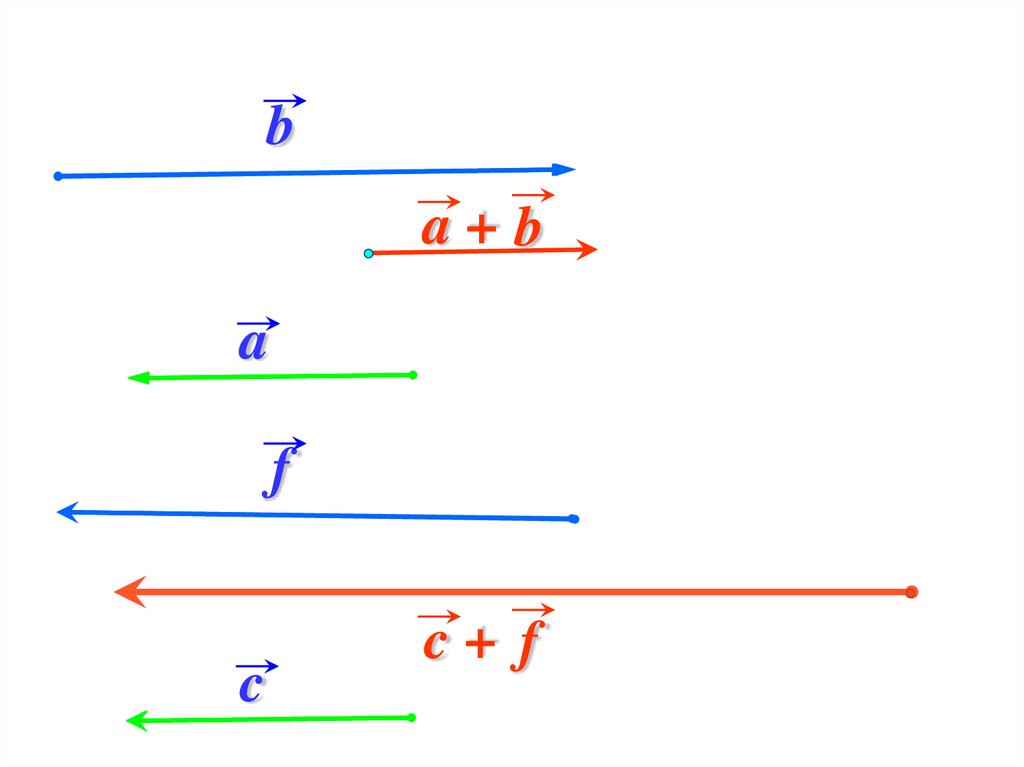
ba+b
a
f
c
c+ f
9.
Законы сложения векторовТеорема
Для любых векторов
1
a, b, c справедливы равенства:
a+b=b+a
!
переместительный закон
2 (a + b) + c = a + (b + c)
сочетательный закон
!
10.
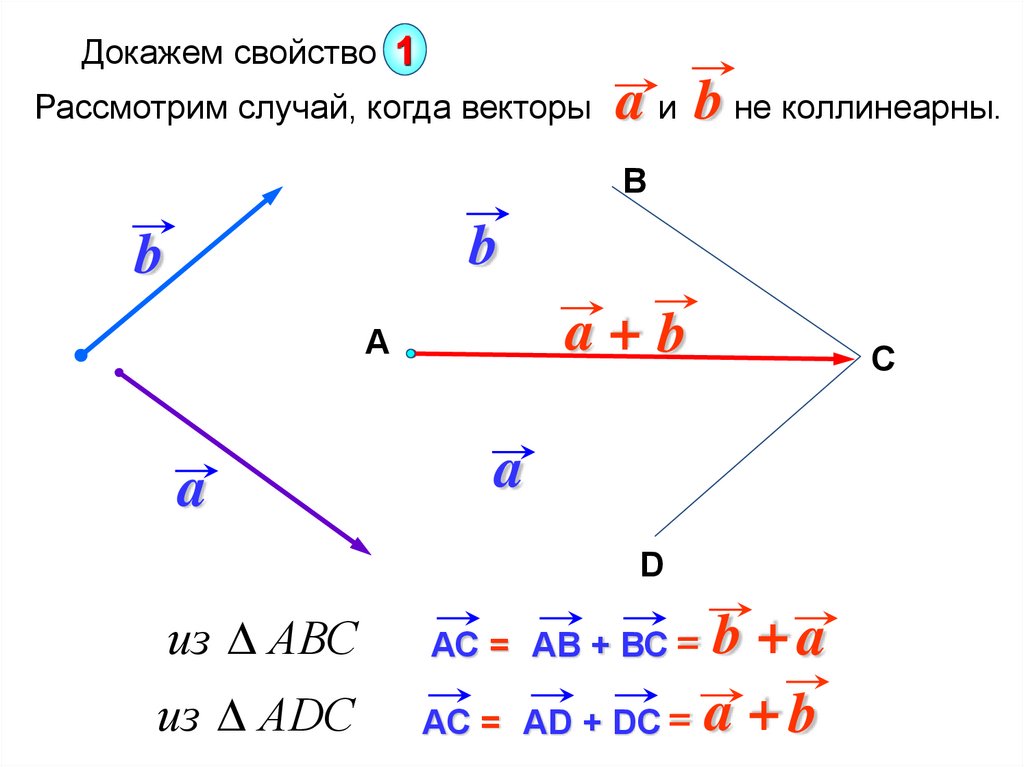
Докажем свойство 1Рассмотрим случай, когда векторы
a и b не коллинеарны.
В
b
b
a+b
А
a
a
D
из АВС
из АDС
b +a
АС = АD + DС = a + b
АС = АВ + ВС =
C
11.
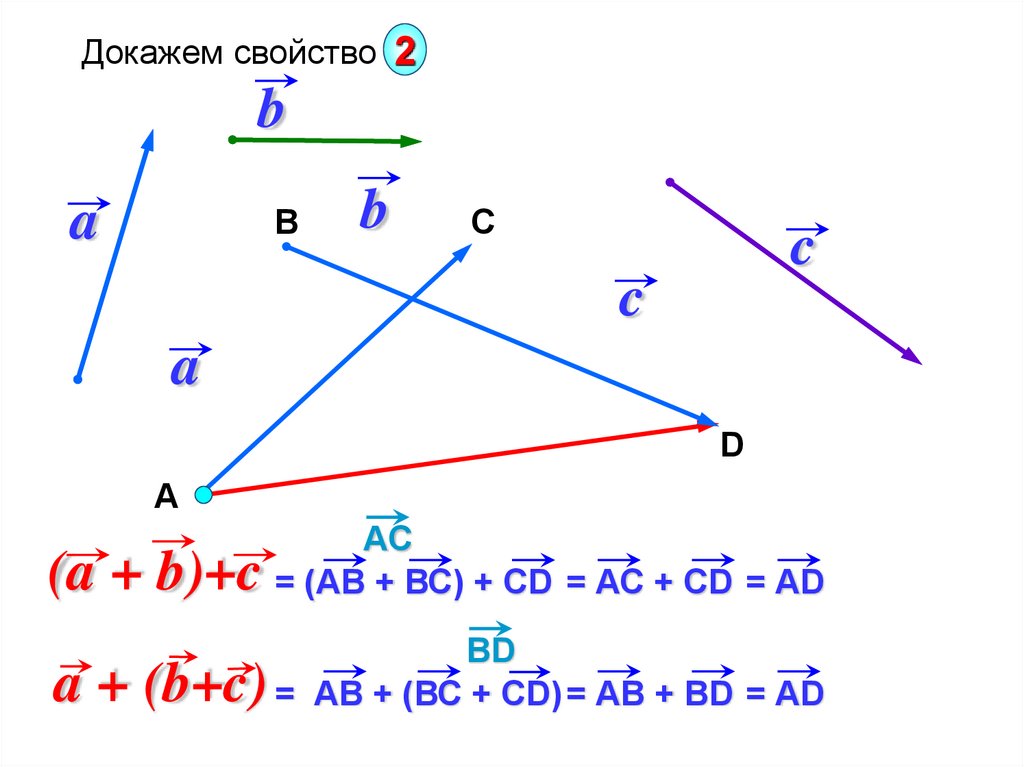
Докажем свойство 2b
a
В
b
C
c
c
a
D
А
(a + b)+c
АC
= (АВ + ВС) + CD = АС + CD = АD
a + (b+c)
BD
= АВ + (ВС + CD) = АB + BD = АD

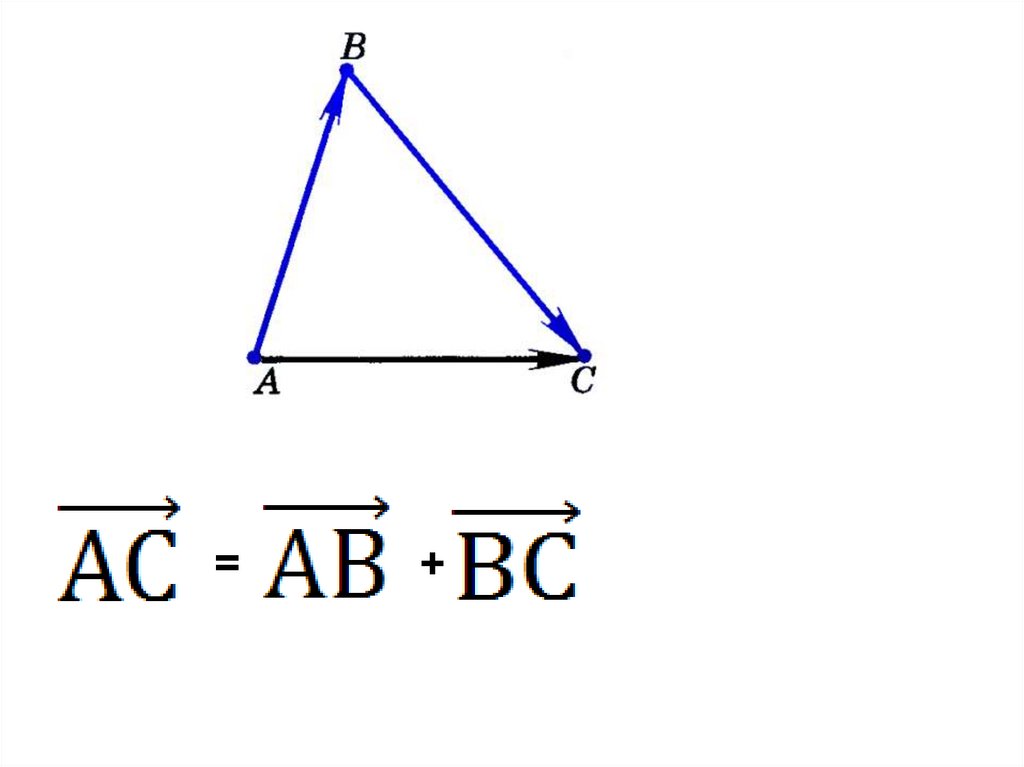



 mathematics
mathematics








