лек-10

1. Моделирование одномерных временных рядов

2. Опр. Временной (динамический) ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или

периодов времени.
• Пространственные модели – модели,
построенные по данным, характеризующим
совокупность различных объектов в определенный
момент времени;
• Модели временных рядов – модели,
построенные по данным, характеризующим один
объект за ряд последовательных моментов времени.
• Классификация факторов, под влиянием которых
формируются значения временного ряда:
– факторы, формирующие тенденцию ряда;
– факторы, формирующие циклические колебания ряда;
– случайные факторы.

3.

• Аддитивная модель временного ряда –
модель, в которой ряд представлен как сумма тенденции,
циклической и случайной компонент.
• Мультипликативная модель временного ряда
– модель, в которой ряд представлен как произведение
тенденции, циклической и случайной компонент.
• Задачи эконометрического исследования
временных рядов:
– выявление и количественное описание каждой
компоненты;
– прогнозирование будущих значений ряда;
– построение моделей взаимосвязи двух или более
временных рядов.

4. Автокорреляция элементов временного ряда

• Опр. Автокорреляция элементов временного ряда –
корреляционная зависимость между последовательными
элементами временного ряда.
• Опр. Лаг – число периодов, по которым рассчитывается
коэффициент автокорреляции между парами элементов
ряда.
• Опр. Автокорреляционная функция временного ряда –
последовательность коэффициентов автокорреляции с
лагами, равными 1, 2, 3 ….
• Замечание. С увеличением лага число пар значений, по которым
рассчитывается коэффициент автокорреляции уменьшается.
Для
статистической достоверности используется правило: максимальный
лаг не больше n/4.

5. Пример 1 Потребление электроэнергии жителями региона за 16 кварталов

• Вывод:
– имеются сезонные колебания периодичностью в
четыре квартала.

6. Моделирование тенденции временного ряда

• Аналитическое выравнивание временного ряда – построение
аналитической функции, характеризующей зависимость
элементов ряда от времени, или тренда.
• Для построения тренда используются функции:
– линейная:
– гиперболическая:
– экспоненциальная:
yˆ t t
yˆt / t
ˆyt e a bt t
– степенная:
yˆ t t
– полиномиальная:
ˆyt 1t 2t 2 ... k t k

7. Способы определения типа тенденции:

• качественный анализ изучаемого процесса путем построения
графика зависимости членов ряда от времени;
• вычисление коэффициентов автокорреляции разного порядка;
• вычисление коэффициентов автокорреляции разного порядка для
исходного и преобразованного ряда и их сравнение
– если имеется большое различие, то это говорит о наличии
нелинейной тенденции ;
• перебор основных форм тренда и выбор уравнения тренда по
максимальному значению коэффициента детерминации.
• Пример 2 Имеются помесячные данные о темпах роста номинальной
заработной платы за 10 месяцев в процентах к уровню декабря
предыдущего года.
• Выводы:
– по графику видно наличие возрастающей тенденции;
– коэффициенты автокорреляции показывают наличие тенденции;
– небольшое различие коэффициентов по членам ряда и их логарифмам
говорит о возможности нелинейной тенденции;
– по коэффициенту детерминации наилучшим является степенной тренд:
yˆ t 80,32 t
0 ,193

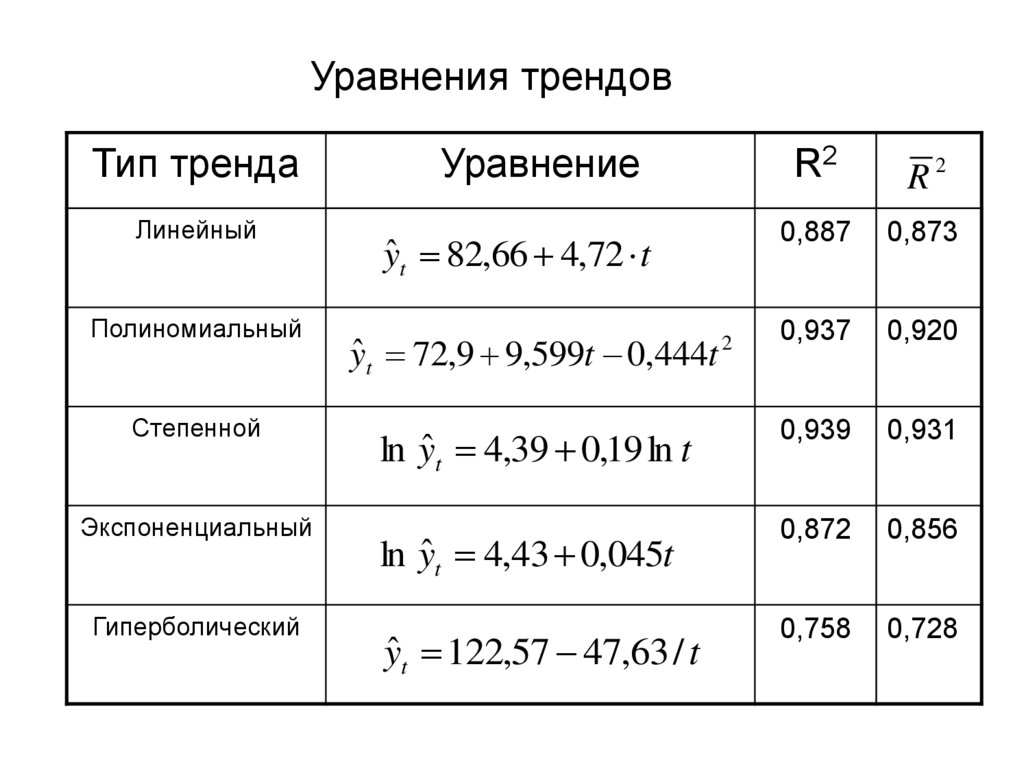
8. Уравнения трендов

Тип тренда
Линейный
Полиномиальный
Степенной
Экспоненциальный
Гиперболический
Уравнение
R2
R2
yˆ t 82,66 4,72 t
0,887
0,873
0,937
0,920
ln yˆ t 4,39 0,19 ln t
0,939
0,931
ln yˆ t 4,43 0,045t
0,872
0,856
yˆ t 122,57 47,63 / t
0,758
0,728
yˆ t 72,9 9,599t 0,444t
2

9. Моделирование сезонных и циклических колебаний

• Два подхода
– Расчет сезонной компоненты методом скользящей средней и
построение аддитивной или мультипликативной модели;
– применение фиктивных переменных.
• Аддитивная модель
Y=T+S+E
• Мультипликативная модель
Y=TSE
• T - трендовая составляющая,
• S – циклическая (сезонная) составляющая,
• E – случайная составляющая.

10. Алгоритм построения модели

• 1. Выравнивание исходного ряда методом скользящей
средней.
• 2. Расчет сезонной компоненты S.
• 3. Устранение сезонной компоненты из исходных
членов ряда и получение выравненных данных (T+E) в
аддитивной модели или (TE) в мультипликативной
модели.
• 4. Аналитическое выравнивание уровней (T+E) или
(TE) и расчет значений T с использованием
полученного уравнения тренда.
• 5. Расчет полученных по модели значений (T+S) или
(TS).
• 6. Расчет абсолютных и/или относительных ошибок.