Similar presentations:
Сетевые модели
1. Сетевые модели
РусановГеология
Семенов
Зотова
Цветоводство
Шляпина
Танцы
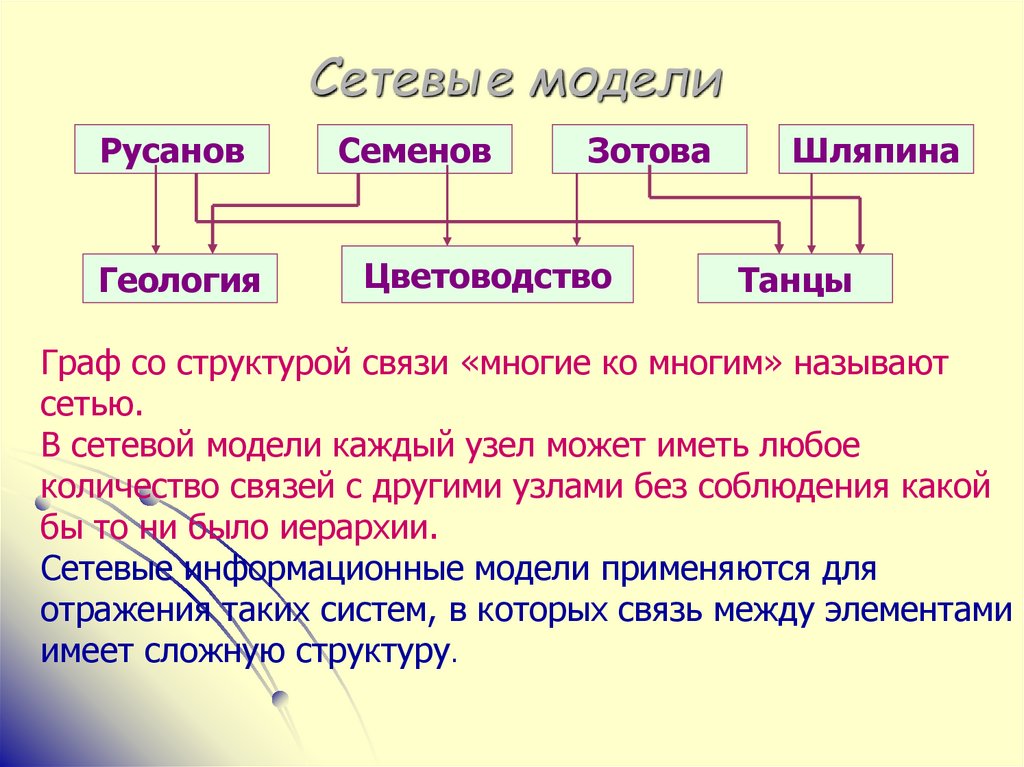
Граф со структурой связи «многие ко многим» называют
сетью.
В сетевой модели каждый узел может иметь любое
количество связей с другими узлами без соблюдения какой
бы то ни было иерархии.
Сетевые информационные модели применяются для
отражения таких систем, в которых связь между элементами
имеет сложную структуру.
2. Сетевые модели
Сетевые модели — способ исследования и проектированиясложных систем, анализа и оптимизации процессов,
состоящих из связанных подсистем или совокупности
последовательных и взаимосвязанных работ и событий.
СМ позволяют дать ответы на следующие вопросы:
как наилучшим образом распределить исполнителей,
чтобы выполнить разработку в срок;
как определить вероятное время выполнения разработки
и выделить те работы, которые наиболее сильно влияют на
срок завершения;
откуда взять ресурсы, если некоторые работы срываются;
как распределить ресурсы (рабочую силу, материалы,
финансы), чтобы не было простоев и авралов.
3. Сетевые модели
Основные понятияСетевая модель базируется на теории ориентированных графов.
Сетевой график — отображение сетевой модели в виде орграфа.
Основными элементами сетевого графика являются:
работа — процесс, связанный с затратами времени и ресурсов
либо только времени и приводящий к достижению определенных
результатов;
ресурсы — материалы, сырье, оборудование, контингент
исполнителей, необходимый для производства работы,
финансовые средства и прочее.
Рис. 2. Пример простейшей сетевой
4. Сетевые модели
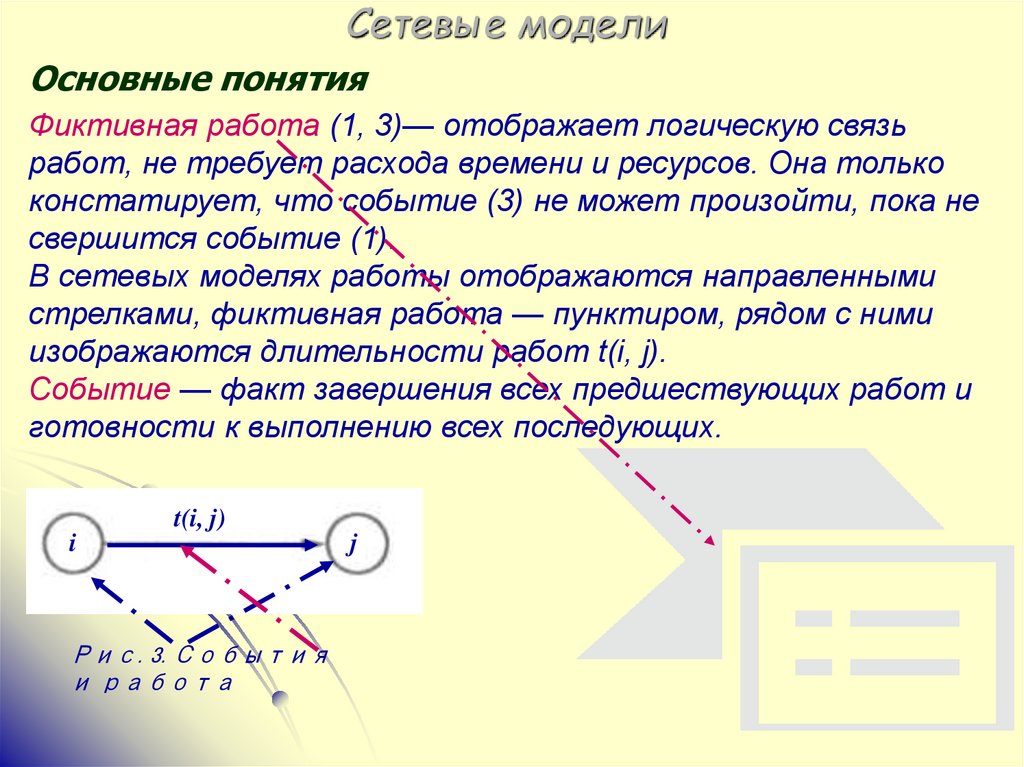
Основные понятияФиктивная работа (1, 3)— отображает логическую связь
работ, не требует расхода времени и ресурсов. Она только
констатирует, что событие (3) не может произойти, пока не
свершится событие (1).
В сетевых моделях работы отображаются направленными
стрелками, фиктивная работа — пунктиром, рядом с ними
изображаются длительности работ t(i, j).
Событие — факт завершения всех предшествующих работ и
готовности к выполнению всех последующих.
t(i, j)
i
Рис. 3. События
и работа
j
5. Сетевые модели
Основные понятияКаждая работа в сети характеризуется:
начальным событием — (i);
конечным событием — (j);
Работы кодируются в терминах событий, т. е. каждая из них
идентифицируется своими начальным и конечным событиями.
Исходное событие («самое начальное») сети (0) иногда
обозначается (I); завершающее событие («самое конечное») —
(С).
Путь — последовательность работ в сети, в которой
конечное событие любой работы совпадает с начальным
событием следующей за ней работы.
Путь кодируется в событиях, через которые он проходит,
например, путь (3, 5, 6) (или (3—5—6); иногда он обозначается
начальным и конечным событиями пути — L(3, 6).
6. Сетевые модели
Основные понятияМогут быть определены следующие типы путей:
1. частичные:
путь, соединяющий два любых события i и j — L(i,j), например, (1, 3,
5) для i = 1, j = 5;
путь от исходного события до данного i-го —L(I, j), например, если i
= 3, то это пути (0, 1, 3) и (0, 3);
путь от данного i-го события до конечного — L(i, С); если i = 3, то
это (3, 5, 6).
7. Сетевые модели
Основные понятия2. Полные пути — от начального события до конечного события,
обозначаются Li, например, 5 полных путей:
L1 = (0, 1, 4, 6); L2 = (0, 1, 3, 5, 6); L3 = (0, 3, 5, 6);
L4 = (0, 2, 5, 6); L5 = (0, 2, 6).
Если известны все длительности работ на СМ, то можно определить
продолжительность любого пути: T ( L) t (i, j )
( i , j ) L
Например, для L1 T(L1) = 28.
T(L2) = 30
T(L3) = 27
T(L4) = 23
T(L5) = 21
8. Сетевые модели
Основные понятияПуть, имеющий наибольшую продолжительность, называется
критическим (LKp), и длительность его обозначается Ткр. На графе это
L2 LKp = (0, 1, 3, 5, 6); Ткр = 30. Работы, находящиеся на критическом
пути, называются критическими. Это работы (0, 1), (1, 3), (3, 5), (5, 6).
Критические работы выделяются на СМ полужирными или двойными
стрелками.
Сам по себе факт обнаружения на сложной СМ критического пути и
критических работ является достаточно важным результатом,
позволяющим выявить узкие места проекта и сосредоточить на них
максимальное внимание.
Время выполнения проекта в целом не
может быть меньше Ткр, поэтому первая
задача при анализе СМ — выявление LKp и
критических работ и поиск возможностей
по сокращению их длительности. На этом
базируется и в этом состоит сущность
первого из сетевых методов — метода
критического пути (Critical Path Method).
9. Сетевые модели
Правила составления СМНа рисунке приведен ориентированный граф, содержащий ряд ошибок с
точки зрения СМ:
1. Тупик (Е). Поскольку сеть одноцелевая, такое звено запрещено.
2. Имеется два исходных события — (А) и (Г).
3. Граф содержит цикл (Б, В, Д) — такие работы никогда не закончатся.
Выводы:
1. Начальное и конечное
событие должны
быть в единственном
экземпляре.
2. Не должно быть
циклов.
10. Сетевые модели
Правила составления СМ3. нельзя допускать работ с одинаковыми i и j, поскольку каждая работа
идентифицируется своими начальным и конечным событиями (рис. а). В
этом случае следует ввести фиктивные работы (рис. б), которые
обеспечивают необходимую развязку;
4. определения событий должны нести максимум информации, например,
если для начала работы (Т, У), (рис. в) нужны результаты только (П, Т) и
(Р, Т), то следует это отразить (например, используя фиктивные работы,
рис. г).
Неточности
Их
устранение
11. Сетевые модели
Правила нумерации событийДля любой работы СМ номер начального события должен быть меньше
номера конечного события (i < j) и каждый путь должен проходить по
возрастающей последовательности номеров событий. Алгоритм
нумерации событий (вычеркивания дуг), который также позволяет
обнаруживать структурные ошибки:
отыскивается начальное (I) событие (в него не входит ни одна работа),
ему присваивается номер 0;
зачеркиваются работы, выходящие из него;
определяются события, не
имеющие теперь входящих работ
(первый ранг), нумеруются в
произвольном порядке 1, 2 или 2, 1;
зачеркиваются работы,
выходящие из них, определяются
события второго ранга;
по достижении конечного
события (С) процесс прекращается.
12. Сетевые модели
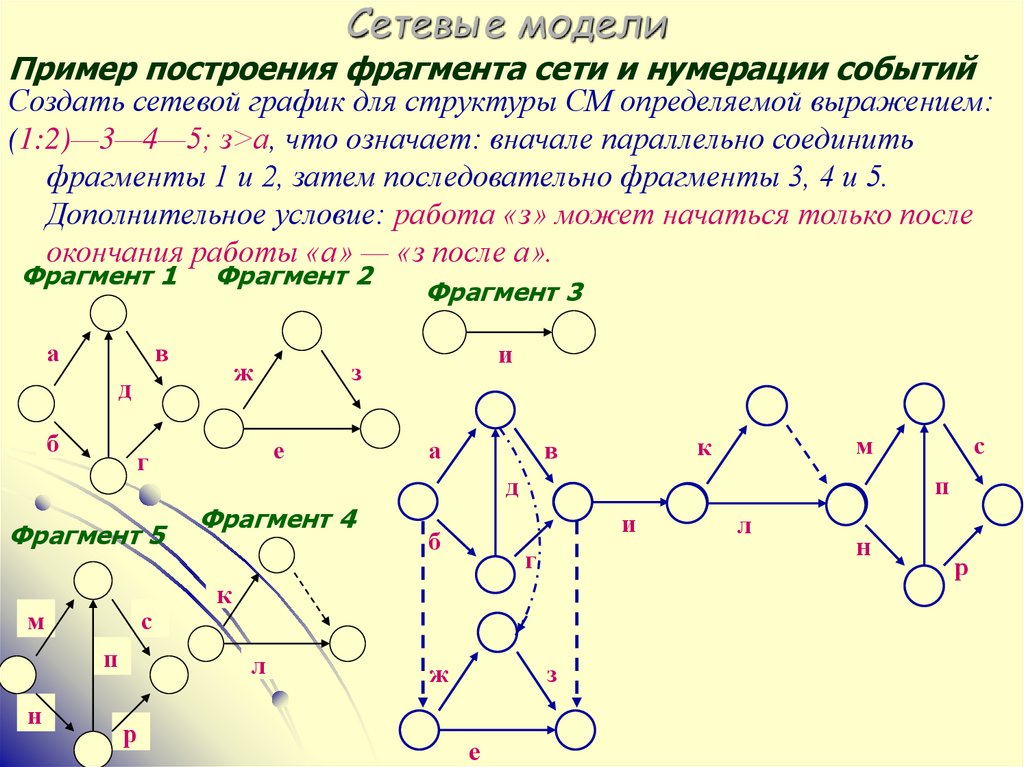
Пример построения фрагмента сети и нумерации событийСоздать сетевой график для структуры СМ определяемой выражением:
(1:2)—3—4—5; з>а, что означает: вначале параллельно соединить
фрагменты 1 и 2, затем последовательно фрагменты 3, 4 и 5.
Дополнительное условие: работа «з» может начаться только после
окончания работы «а» — «з после а».
Фрагмент 1
а
Фрагмент 2
в
ж
д
б
Фрагмент 5
м
с
п
н
а
м
к
в
Фрагмент 4
и
б
г
к
ж
з
е
с
п
д
л
р
и
з
е
г
Фрагмент 3
л
н
р
13. Сетевые модели
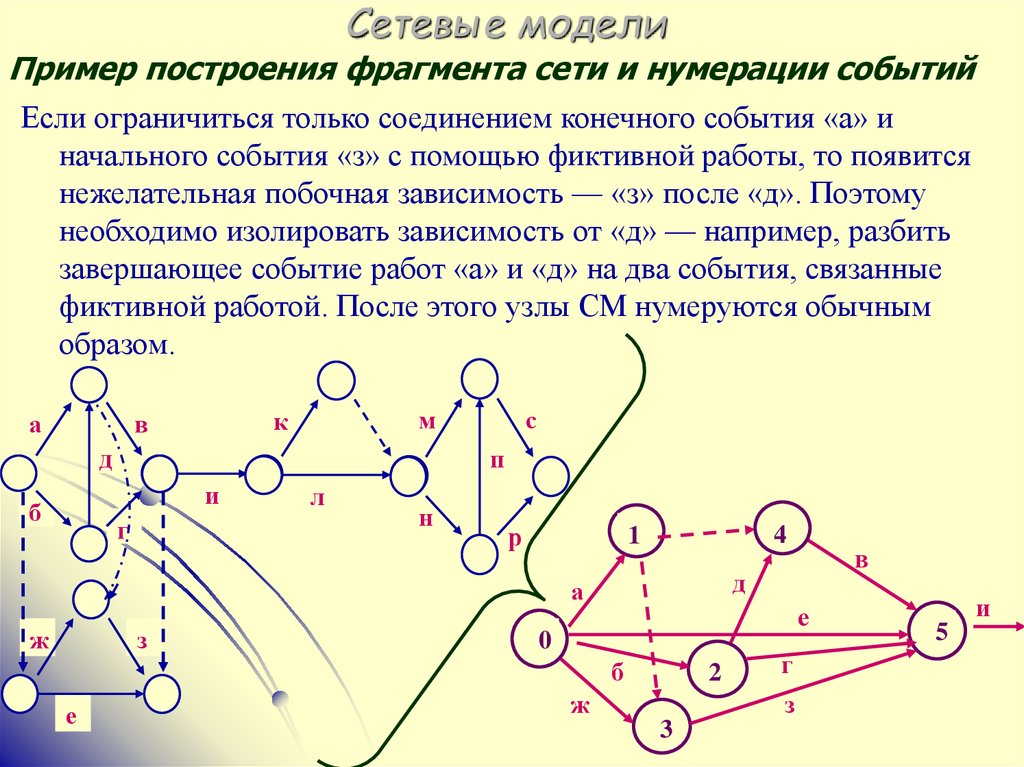
Пример построения фрагмента сети и нумерации событийЕсли ограничиться только соединением конечного события «а» и
начального события «з» с помощью фиктивной работы, то появится
нежелательная побочная зависимость — «з» после «д». Поэтому
необходимо изолировать зависимость от «д» — например, разбить
завершающее событие работ «а» и «д» на два события, связанные
фиктивной работой. После этого узлы СМ нумеруются обычным
образом.
а
м
к
в
п
д
и
б
с
г
л
н
р
4
1
д
а
ж
з
е
0
б
е
в
2
ж
г
з
3
и
5
14. Сетевые модели
УкрупнениеСетевые модели
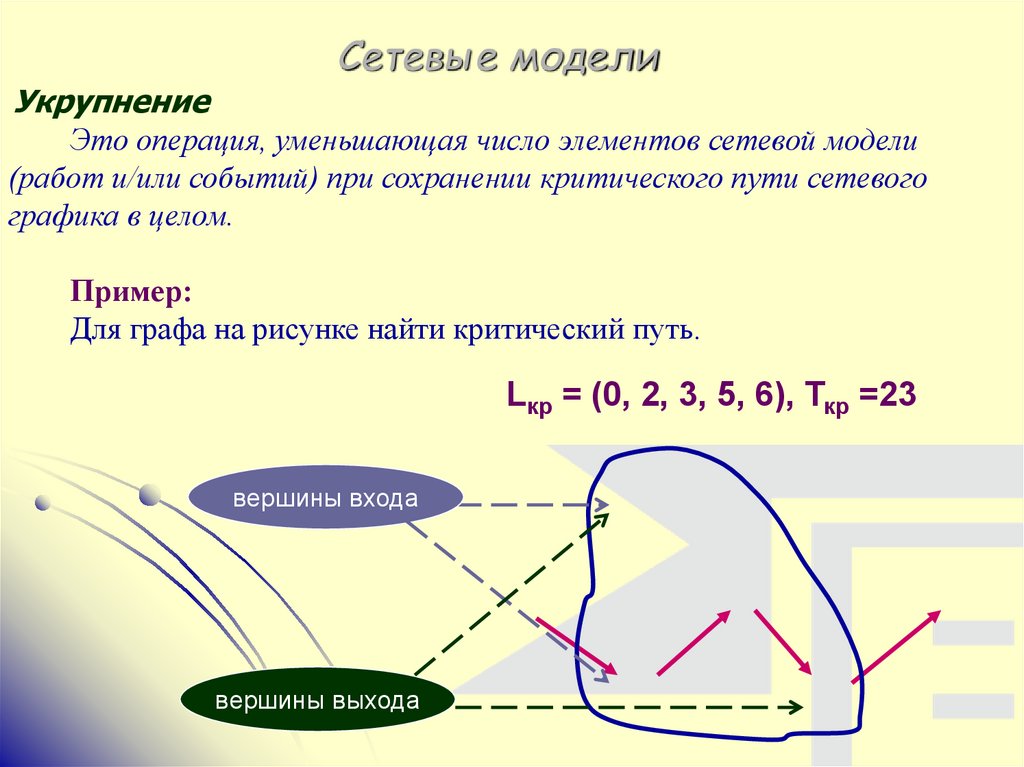
Это операция, уменьшающая число элементов сетевой модели
(работ и/или событий) при сохранении критического пути сетевого
графика в целом.
Пример:
Для графа на рисунке найти критический путь.
Lкр = (0, 2, 3, 5, 6), Ткр =23
вершины входа
вершины выхода
15. Сетевые модели
УкрупнениеСетевые модели
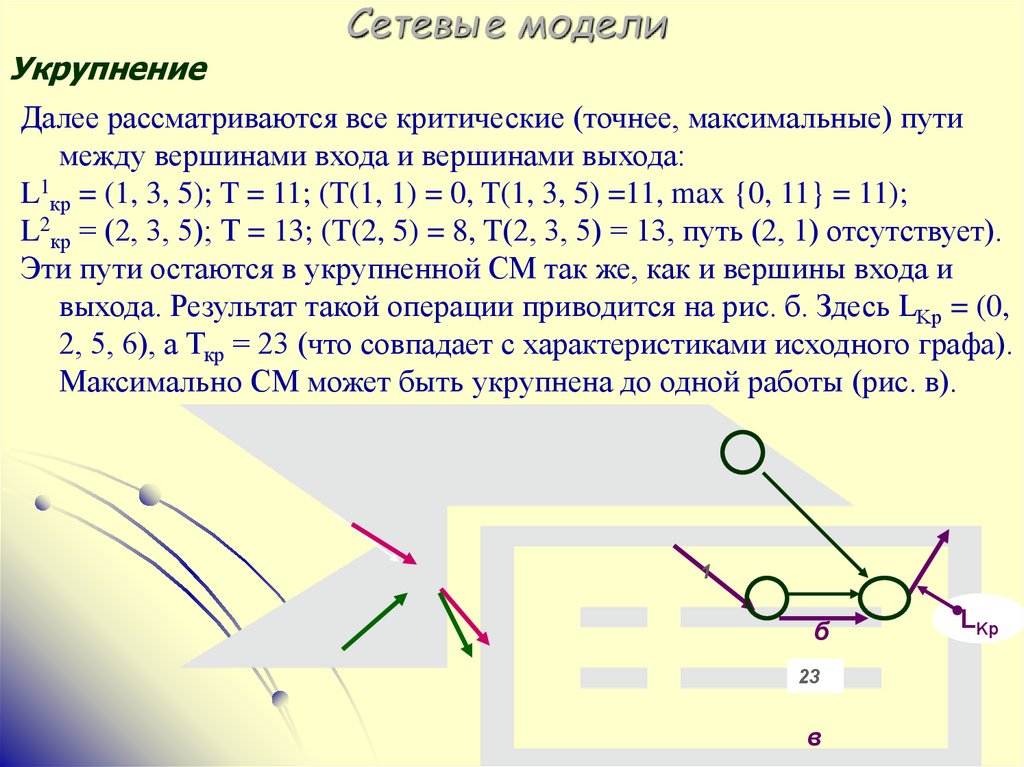
Далее рассматриваются все критические (точнее, максимальные) пути
между вершинами входа и вершинами выхода:
L1кp = (1, 3, 5); T = 11; (T(1, 1) = 0, T(1, 3, 5) =11, max {0, 11} = 11);
L2кp = (2, 3, 5); Т = 13; (T(2, 5) = 8, T(2, 3, 5) = 13, путь (2, 1) отсутствует).
Эти пути остаются в укрупненной СМ так же, как и вершины входа и
выхода. Результат такой операции приводится на рис. б. Здесь LKр = (0,
2, 5, 6), а Ткр = 23 (что совпадает с характеристиками исходного графа).
Максимально СМ может быть укрупнена до одной работы (рис. в).
1
б
23
в
LKр
16. Сетевые модели
РазукрупнениеСетевые модели
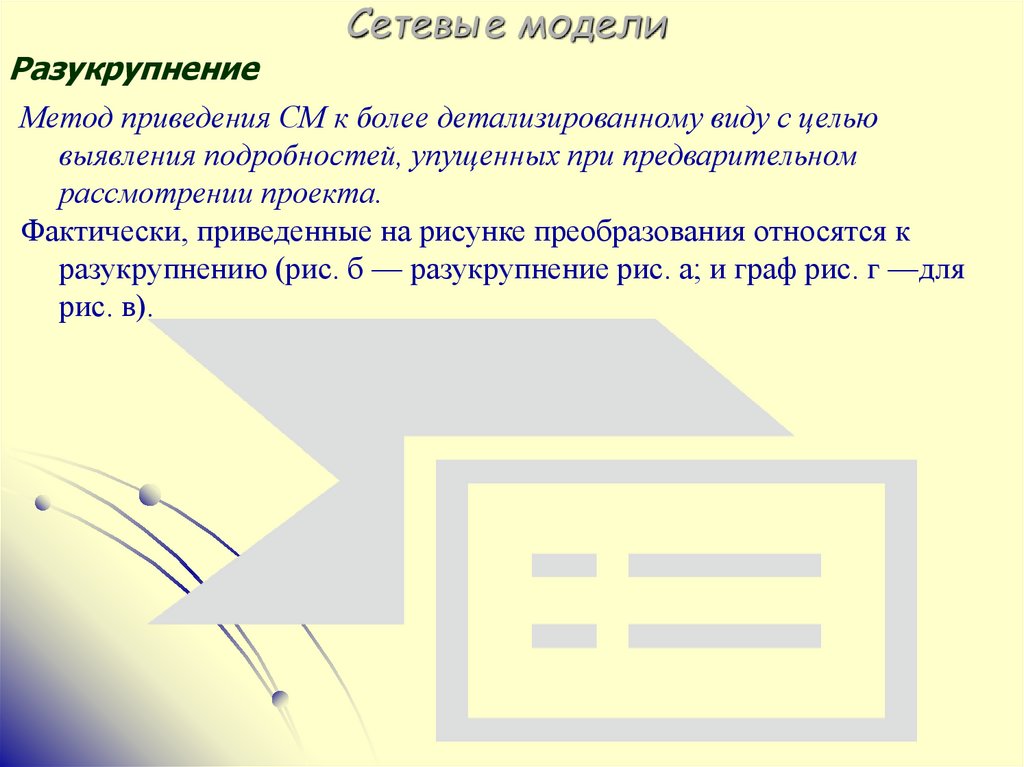
Метод приведения СМ к более детализированному виду с целью
выявления подробностей, упущенных при предварительном
рассмотрении проекта.
Фактически, приведенные на рисунке преобразования относятся к
разукрупнению (рис. б — разукрупнение рис. а; и граф рис. г —для
рис. в).
17. Сетевые модели
Декомпозиция СМСетевые модели
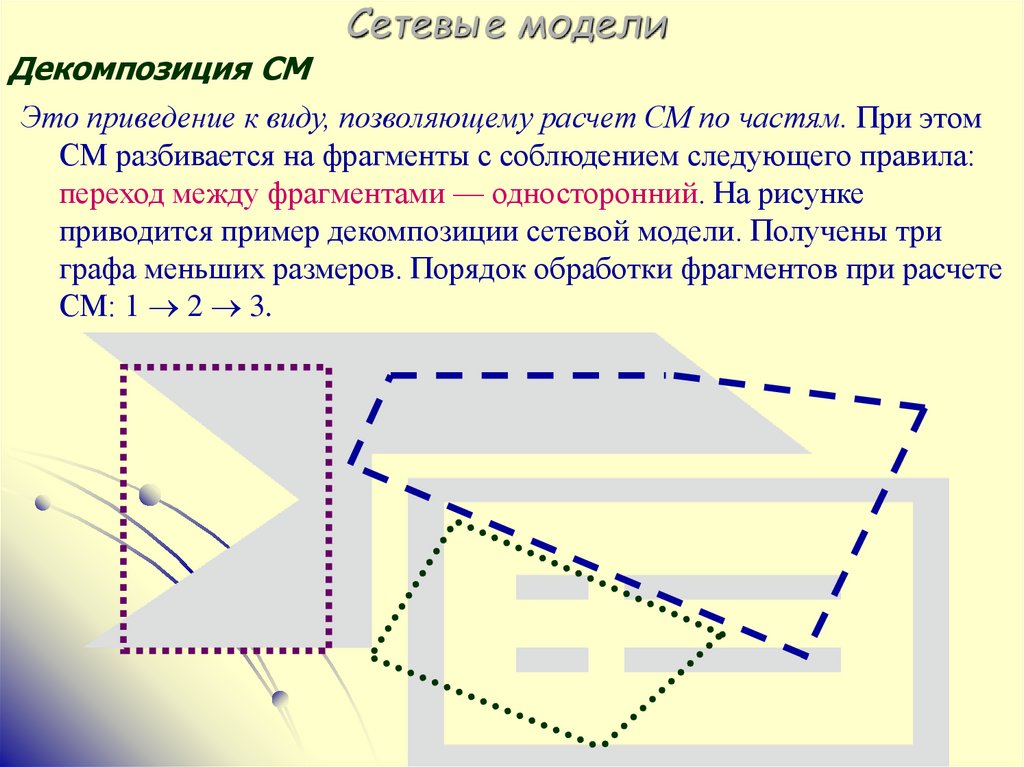
Это приведение к виду, позволяющему расчет СМ по частям. При этом
СМ разбивается на фрагменты с соблюдением следующего правила:
переход между фрагментами — односторонний. На рисунке
приводится пример декомпозиции сетевой модели. Получены три
графа меньших размеров. Порядок обработки фрагментов при расчете
СМ: 1 2 3.









 informatics
informatics








