Similar presentations:
Korrelyatsiyalyқ taldau
1.
Корреляциялықталдау
Доцент: Ахтаева Н.С.
2.
Дәріс жоспары:1. Корреляциялық талдау - ауру асқынуының
қауіп қатер факторын сандық бағалайтын әдіс
ретінде.
2. Шашырау диаграммасы.
3.Пирсонның корреляция коэффициенті.
4.Корреляция коэффициентін бағалаудың
сенімділігі.
3.
Корреляциялық талдауЭпидемиологияның ең маңызды міндеттерінің бірі
қауіп қатер факторы болып табылады.
Медицинада қауіп қатер факторы – бұл аурудың
пайда болуына мүмкіндік туғызатын фактор (мысалы,
темекі тарту - жүрек талмасы немесе қатерлі ісікке
алып келетін қауіп қатер факторы, су жүйесіндегі
болатын апат – іш өту ауруына алып келетін қауіп қатер
факторы).
Ауру асқынуындағы қауіп қатер факторын сандық
жағынан бағалау үшін корреляциялық талдау әдіс
қолданылады.
4.
Корреляциялық байланыс• Корреляциялық байланыс немесе корреляция деп бір
белгінің бір сандық мәніне екінші белгінің бірнеше
мәні (таралуы) сәйкес келетін тәуелділікті айтады.
• Мысалы, 1). Адамның бойының ұзындығы мен дене
салмағының арасында оң байланыс бар екендігі
белгілі, алайда бұл белгілердің мәндерінің арасында
толық сәйкестік жоқ. Бойларының ұзындықтары
бірдей (мысалы, 160 см) адамдарға әртүрлі дене
салмақтары (мысалы, 55, 60, 65 кг) сәйкес келеді.
5.
Корреляциялық байланыс• 2) Сапалық белгілерге қатысты да осыны байқауға
болады: әдетте ақсары адамдардың көздерінің түсі
көкшіл, қара торы адамдарда – қоңыр түсті болып
келеді. Алайда қоңыркөзді ақсары адамдар мен
көздері көкшіл түсті қараторы адамдар да кездеседі.
Бұл биологиялық белгіге генетикалық та, сыртқы
факторлар да ықпал ететіндігімен түсіндіріледі.
6.
Корреляциялық талдауКорреляцилық талдау – бұл екі немесе одан көп кездейсоқ
шамалардың арасындағы байланыстың тығыздығын және
бағытын анықтайтын сандық әдіс.
«Корреляция» терминін алғаш
рет француз палеонтологы Ж.
Кювье енгізді, ал статистикада
оны
Ф.
Гальтон
алғаш
қолданды.
Ж. Кювье
(1769 - 1832)
Ф. Гальтон
(1822 - 1911)
7.
Корреляция коэффициентіКорреляция коэффициенті – байланыстың күшін және оның
бағытын сипаттайтын, [-1, 1] аралығынды мәндерін қабылдайтын
көрсеткіш.
Байланыстың күшін бағалау үшін корреляция теориясында
ағылшын статистигі Чеддоктың шкаласы қолданылады
Байланыс күші
Толық
Күшті
Орта
Әлсіз
Байланыс жоқ
Байланыс сипаты
Тура (+)
Кері (-)
1
-1
0,7 ден 1ге
-0,7 ден -1ге
0,7 ден 0,3ке
-0,7 ден -0,3ке
0,3 ден 0ге
-0,3 тен 0ге
0
0
8.
Корреляциялық байланысБағыты бойынша тура және кері корреляциялық байланыс
деп бөлінеді.
Тура корреляциялық байланыс – бір айнымалының мәндері
өскенде екінші айнымалының мәндері өсетін (су құбырындағы
судағы стандартты емес сынамалар артқан кездеде, іш
сүзегімен аурудың артуы) байланыс.
Кері корреляциялық байланыс – бір айнымалының мәндері
кемігенде екінші айнымалының мәндері өсетін («В»
сарауруына қарсы екпе жұмысының ауқымын көбейткен
сайын, онымен ауыратындардың кемуі) байланыс.
9.
Корреляциялық байланысТура байланыс кезінде корреляция коэффициенті «0»-ден
«+1»-ге дейінгі мәндерді қабылдайды.
Кері байланыс кезінде корреляция коэффициенті «-1»-ден
«0»-ге дейінгі мәндерді қабылдайды.
Егер корреляция коэффициенті «0»-ге тең болса, онда
құбылыстар арасында байланыс болмайды.
Егер корреляция коэффициенті «+1» немесе «–1» болса, онда
құбылыстар арасында байланыс функционалдық болады.
10.
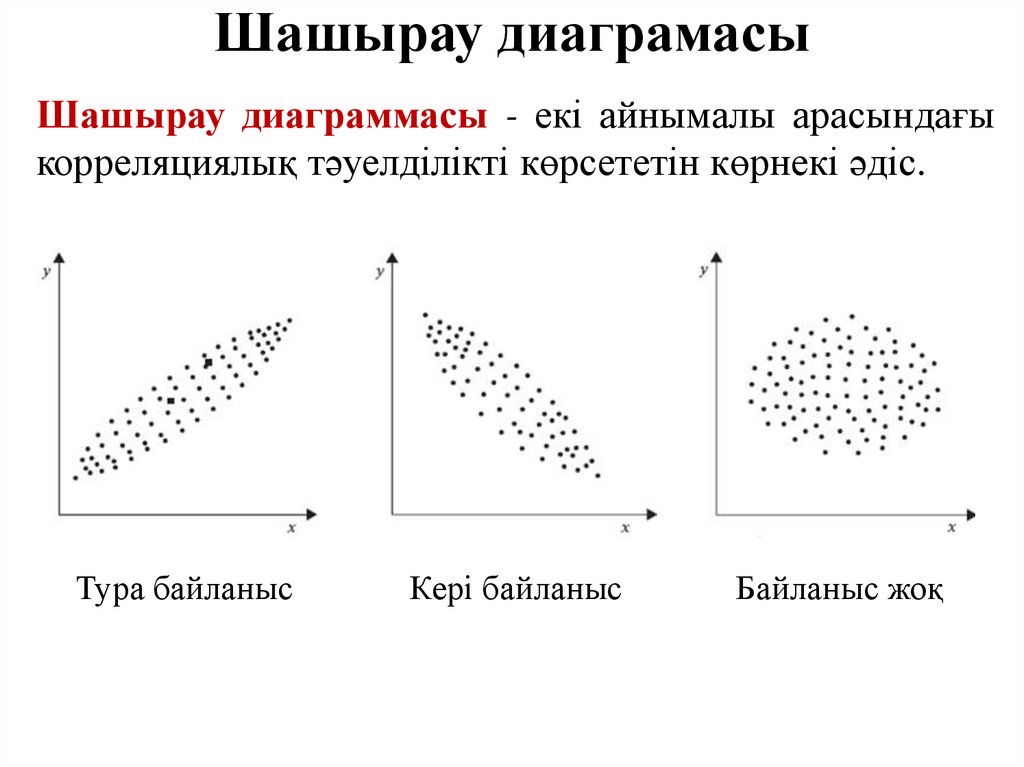
Шашырау диаграмасыШашырау диаграммасы - екі айнымалы арасындағы
корреляциялық тәуелділікті көрсететін көрнекі әдіс.
Тура байланыс
Кері байланыс
Байланыс жоқ
11.
Пирсонның корреляция коэффициентіПирсонның корреляция коэффициенті – байланыстың күшін
және бағытын сипаттайтын көрсеткіш:
мұндағы rxy – корреляция коэффициенті,
х, у – корреляцияланатын қатар,
,
- орташа шамалар.
корреляция коэффициенті параметрлік коэффициент болып
табылады.
12.
Cпирменнің рангілік корреляциякоэффициенті
rs 1
6
2
d
2
n (n 1)
13.
Корреляция коэффициентінің мәнділігіжөніндегі жорамалды тексеру:
1. H және H жорамалдарын анықтаймыз :
0
1
• H0: ρ=0 (корреляция жоқ),
• H1: ρ ≠0. (корреляция бар),
• 2. α мәнділік деңгейін береміз
,
14.
•3. Критерий статистикасын есептейміз:t
r
1 r
2
n 2
t статистикасы еркіндік дәрежесі (n-2) ге
тең болатын Стьюдент таралуы
15.
4. tα,n-2 сыни сыни нүктелерін табамыз.5. Егер │t│ ≥ tсыни , онда H0 жоққа
шығарылады.
Егер │t│ < tсыни , онда H0 қабылданады.
16.
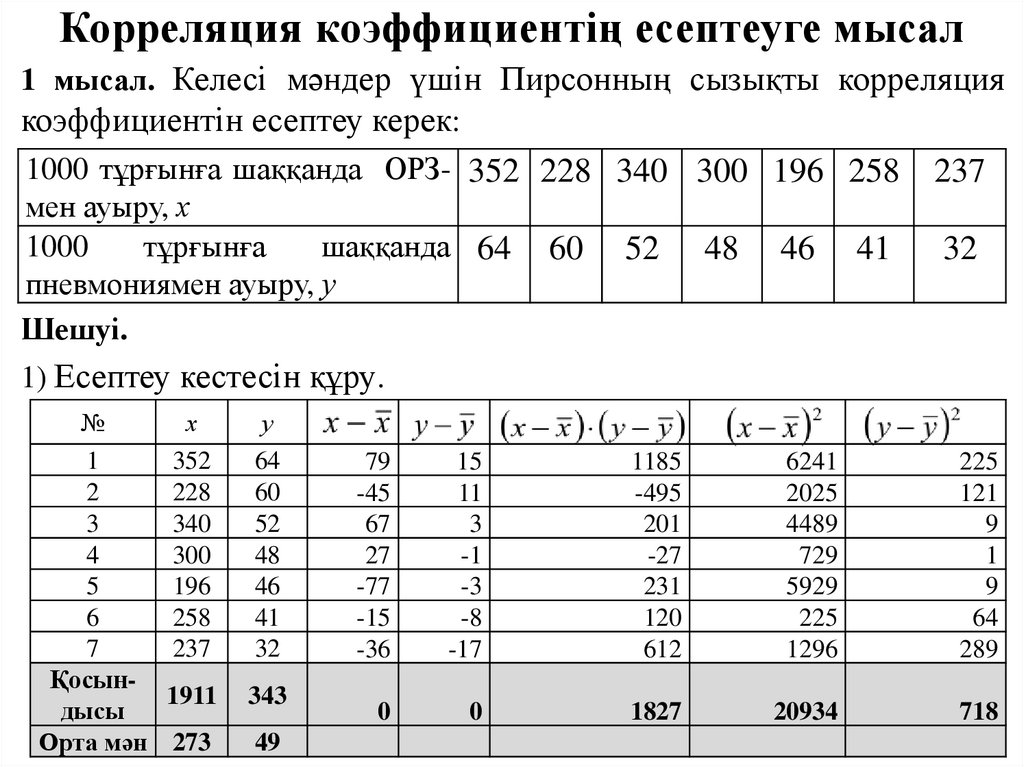
Корреляция коэффициентің есептеуге мысал1 мысал. Келесі мәндер үшін Пирсонның сызықты корреляция
коэффициентін есептеу керек:
1000 тұрғынға шаққанда ОРЗ- 352 228 340 300 196 258
мен ауыру, х
1000
тұрғынға
шаққанда 64 60 52 48 46 41
пневмониямен ауыру, у
Шешуі.
237
32
1) Есептеу кестесін құру.
№
1
2
3
4
5
6
7
Қосындысы
Орта мән
х
352
228
340
300
196
258
237
у
64
60
52
48
46
41
32
1911
343
273
49
79
-45
67
27
-77
-15
-36
15
11
3
-1
-3
-8
-17
1185
-495
201
-27
231
120
612
6241
2025
4489
729
5929
225
1296
225
121
9
1
9
64
289
0
0
1827
20934
718
17.
Корреляция коэффициентің есептеуге мысал1 мысал.
Шешуі (жалғасы).
2) Корреляция коэффициентін есептеу керек:
Алынған нәтижені талдау: қарастырылған
арасындағы байланыс тура, орта.
белгілердің
18.
Корреляция коэффициентің есептеуге мысал1 мысал.
Шешуі (жалғасы).
3) Стьюдент критерийін есептеу керек:

















 medicine
medicine