Similar presentations:
Elektronika dla Informatyków
1.
Elektronikadla
Informatyków
Część 2
1
2.
Sygnały zmienne (AC)Sygnał sinusoidalny
Najbardziej fundamentalny sygnał w elektronice,
ponieważ dowolny inny sygnał może być syntetyzowany
jako suma sygnałów sinusoidalnych o odpowiednich
częstotliwościach i amplitudach
u – napięcie chwilowe oznaczane małą literą, jedn. V
UA – amplituda oznaczana wielką literą, jedn. V
t – czas (s)
f – częstotliwość, jednostka: 1/sekunda = 1Hz (Hertz)
2
3.
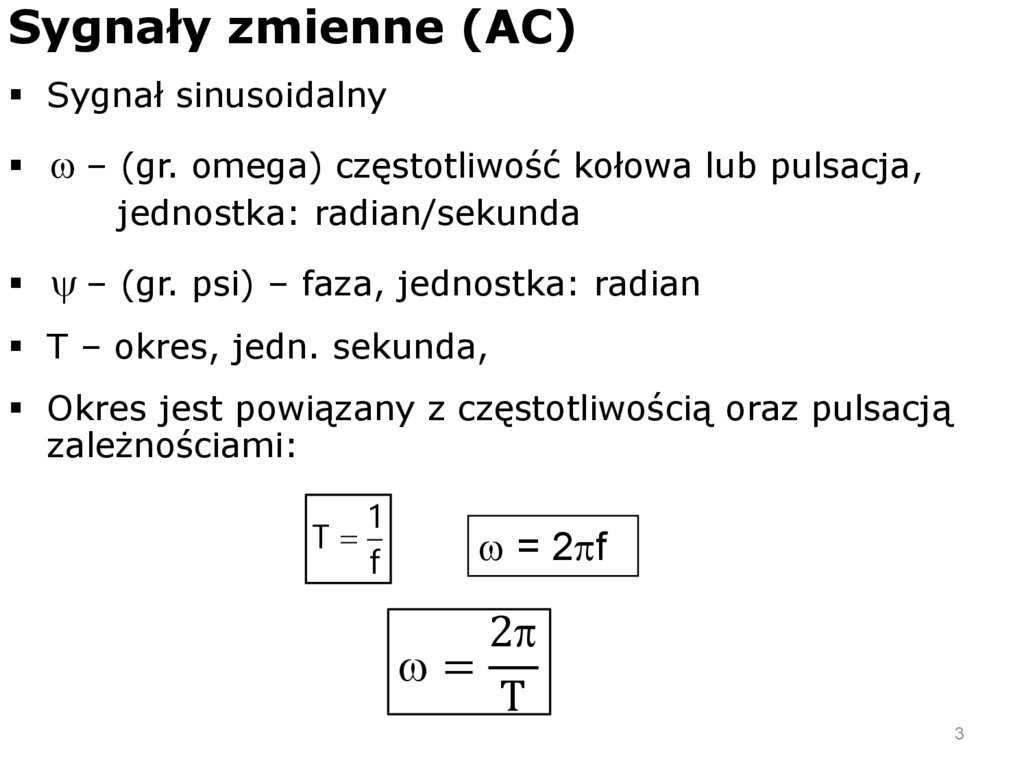
Sygnały zmienne (AC)Sygnał sinusoidalny
w – (gr. omega) częstotliwość kołowa lub pulsacja,
jednostka: radian/sekunda
y – (gr. psi) – faza, jednostka: radian
T – okres, jedn. sekunda,
Okres jest powiązany z częstotliwością oraz pulsacją
zależnościami:
1
T
f
w = 2pf
2p
w =
T
3
4.
Sygnały zmienne (AC)Symbol źródła napięcia zmiennego
U
Symbol ten może dotyczyć napięcia sinusoidalnego lub
napięcia zmiennego o innym przebiegu czasowym
U (wielka litera) oznacza amplitudę napięcia
Przeważnie wielkimi literami będziemy oznaczali
wielkości stałe w czasie a małymi zmienne (chwilowe)
Przykład: U, R – wielkości stałe w czasie
Przykład: u, i – wielkości zmienne w czasie
4
5.
Sygnały zmienne (AC)Sygnał sinusoidalny
Amplituda sygnału sinusoidalnego może być podawana
na wiele sposobów:
Wartość maksymalna UA lub Up
Amplituda międzyszczytowa Vpp = 2UA
Wartość skuteczna (rms – root mean square)
UA
Urms
Up
Vpp
5
6.
Sygnały zmienne (AC)Sygnał sinusoidalny
Wartość skuteczna napięcia sinusoidalnego jest to taka
wartość napięcia stałego, które podane na rezystancję
R przez czas odpowiadający okresowi T, spowoduje
wydzielenie się w tej rezystancji takiej samej ilości
energii cieplnej, co napięcie sinusoidalne w jednym
okresie.
Wartość skuteczna jest związana z amplitudą zależnością:
Urms =
UA
2
= 0,707·UA
Wartość skuteczna Urms wykorzystywana jest w obliczaniu
mocy sygnałów sinusoidalnych
6
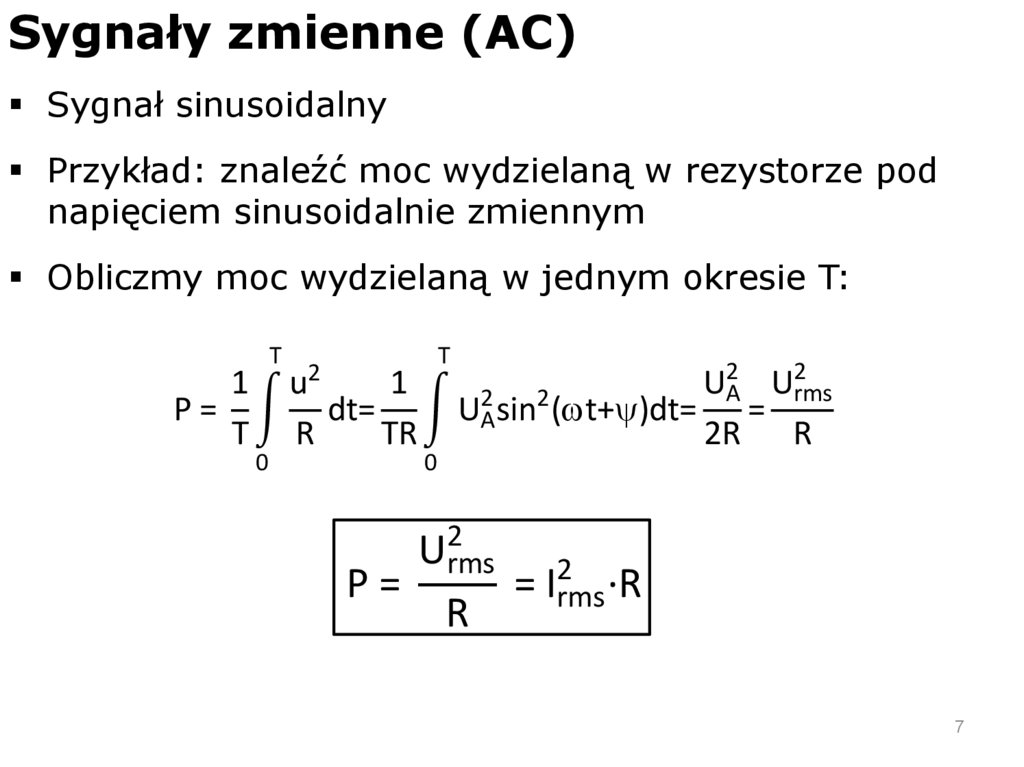
7.
Sygnały zmienne (AC)Sygnał sinusoidalny
Przykład: znaleźć moc wydzielaną w rezystorze pod
napięciem sinusoidalnie zmiennym
Obliczmy moc wydzielaną w jednym okresie T:
1
P =
T
T
0
T
2
u
1
dt=
R
TR
P =
0
2
2
U
U
A
rms
U2A sin2 (wt+y)dt= =
2R R
2
Urms
R
= I2rms ·R
7
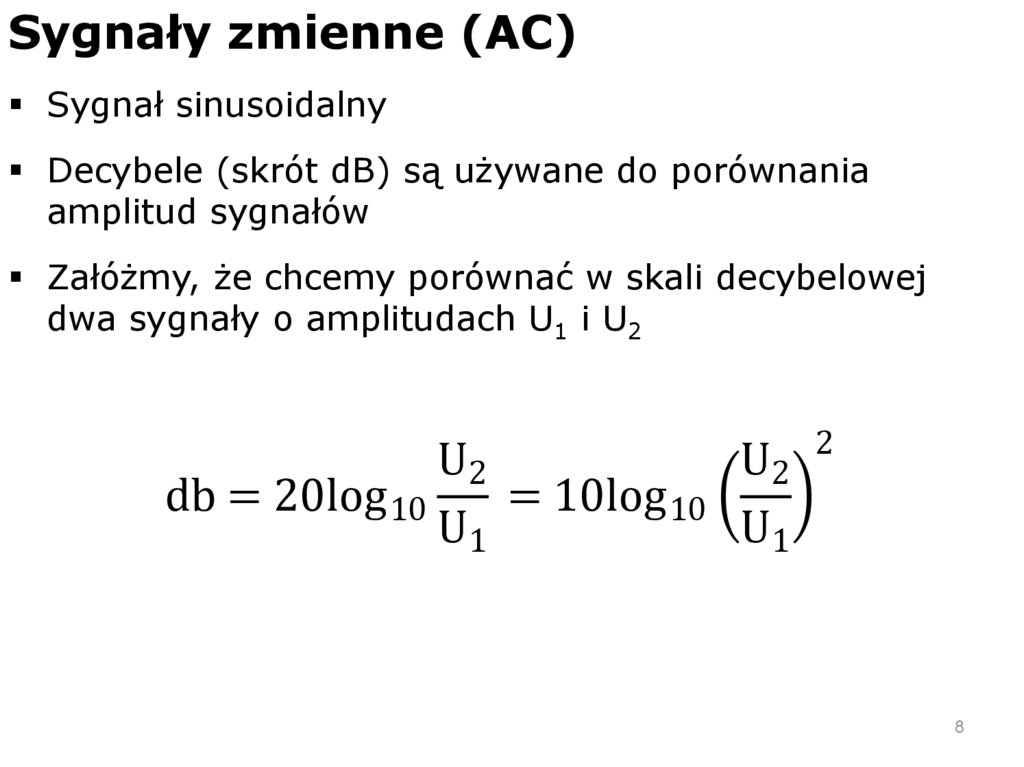
8.
Sygnały zmienne (AC)Sygnał sinusoidalny
Decybele (skrót dB) są używane do porównania
amplitud sygnałów
Załóżmy, że chcemy porównać w skali decybelowej
dwa sygnały o amplitudach U1 i U2
U2
U2
db = 20log 10
= 10log 10
U1
U1
2
8
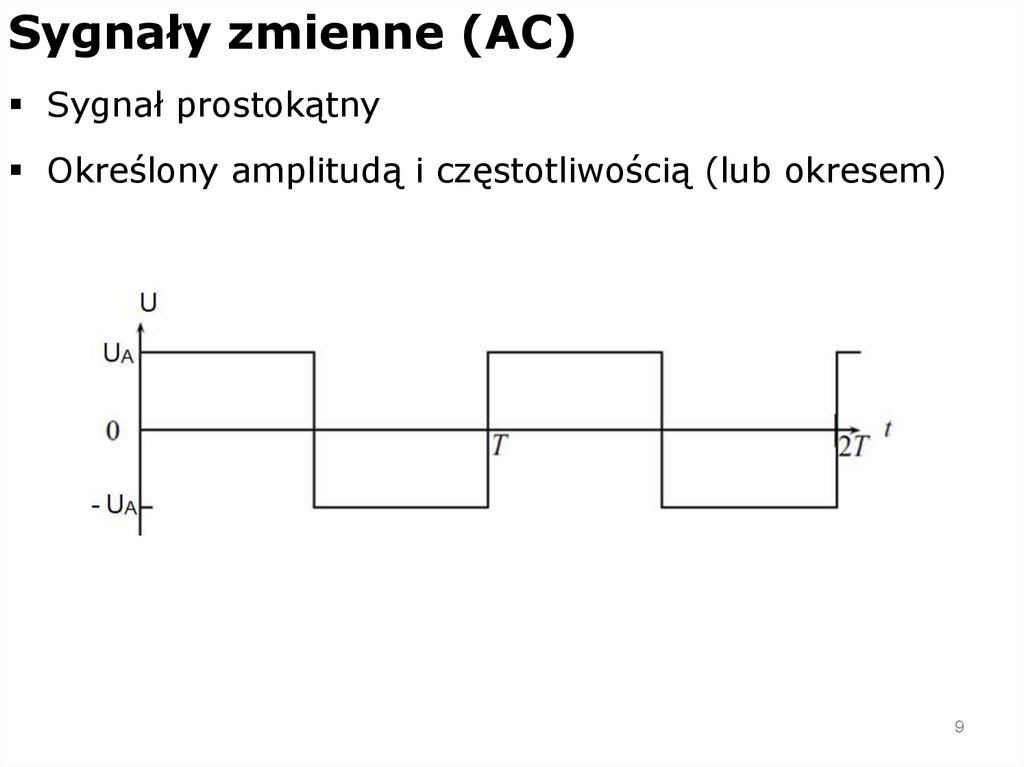
9.
Sygnały zmienne (AC)Sygnał prostokątny
Określony amplitudą i częstotliwością (lub okresem)
9
10.
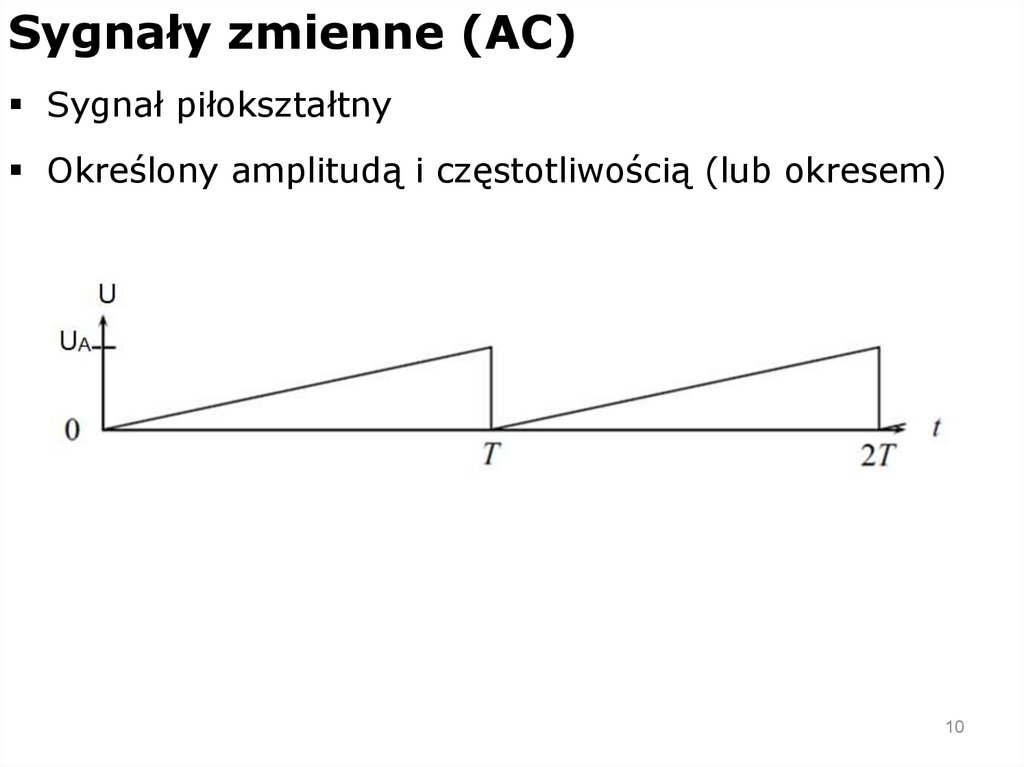
Sygnały zmienne (AC)Sygnał piłokształtny
Określony amplitudą i częstotliwością (lub okresem)
10
11.
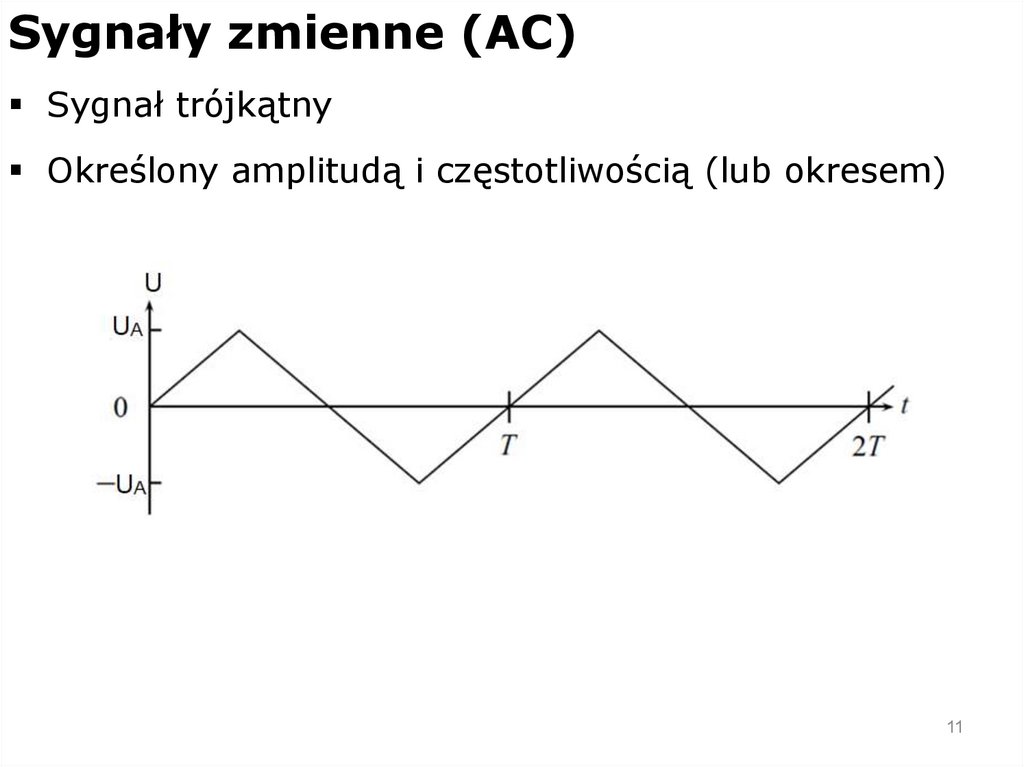
Sygnały zmienne (AC)Sygnał trójkątny
Określony amplitudą i częstotliwością (lub okresem)
11
12.
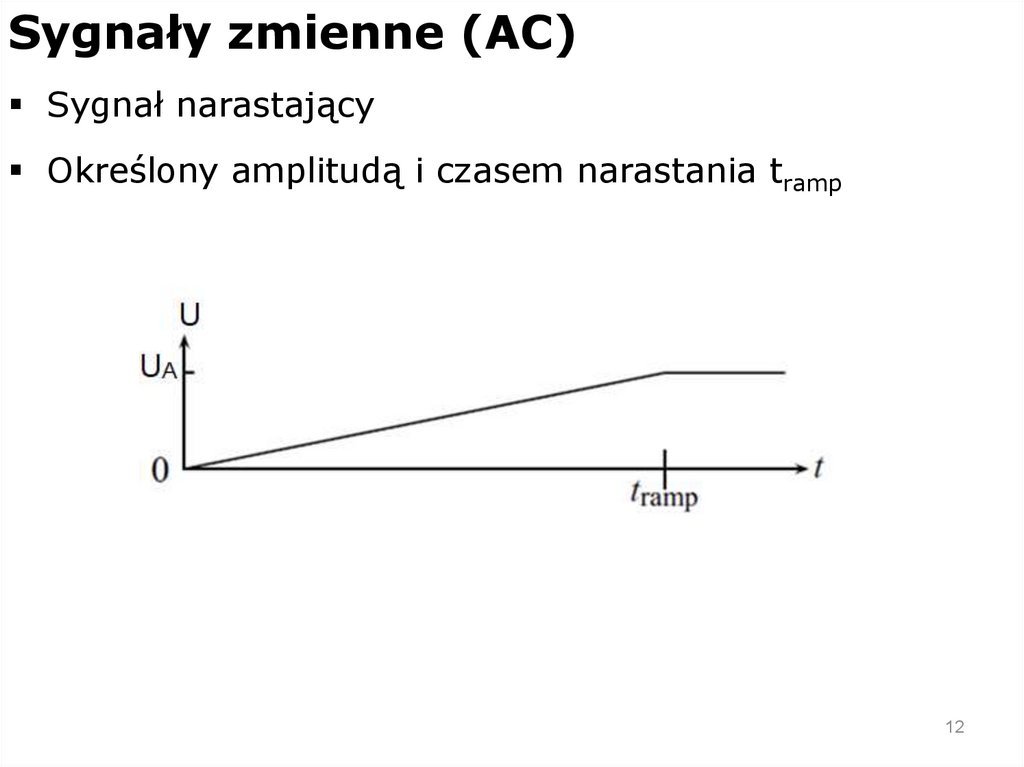
Sygnały zmienne (AC)Sygnał narastający
Określony amplitudą i czasem narastania tramp
12
13.
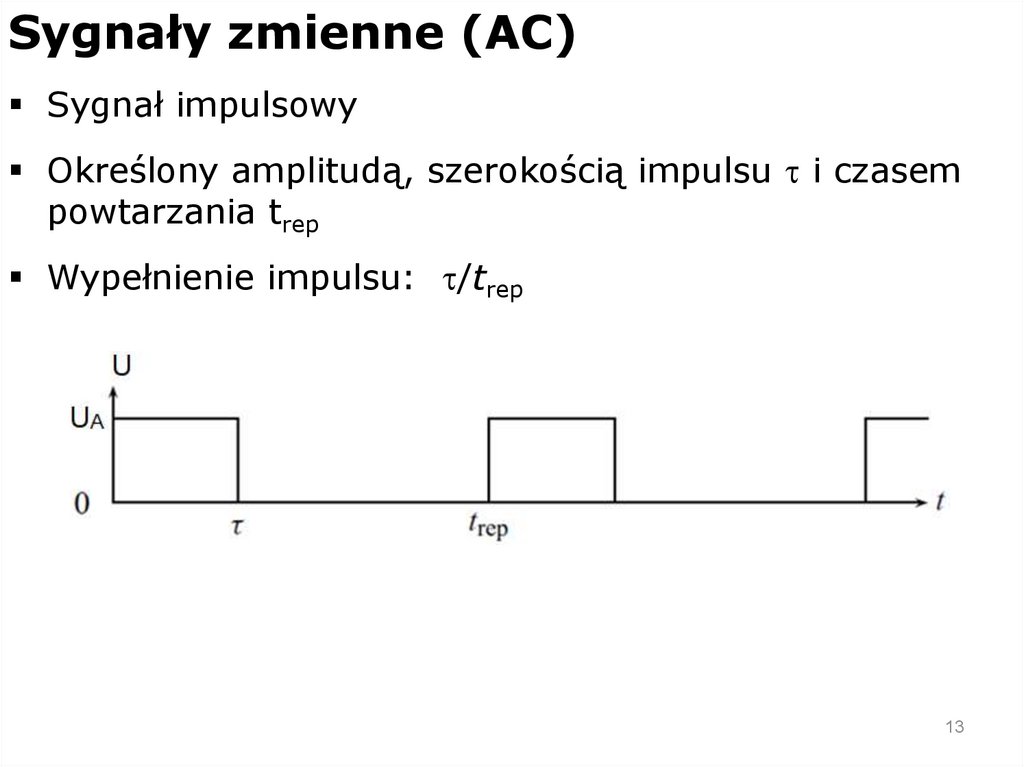
Sygnały zmienne (AC)Sygnał impulsowy
Określony amplitudą, szerokością impulsu t i czasem
powtarzania trep
Wypełnienie impulsu: t/trep
13
14.
Sygnały zmienne (AC)Szum
Szumy to sygnały losowe pochodzenia termicznego
lub inne niepożądane sygnały pojawiające się w
obwodzie.
Szum w uproszczeniu jest opisany zawartymi w nim
częstotliwościami.
14
15.
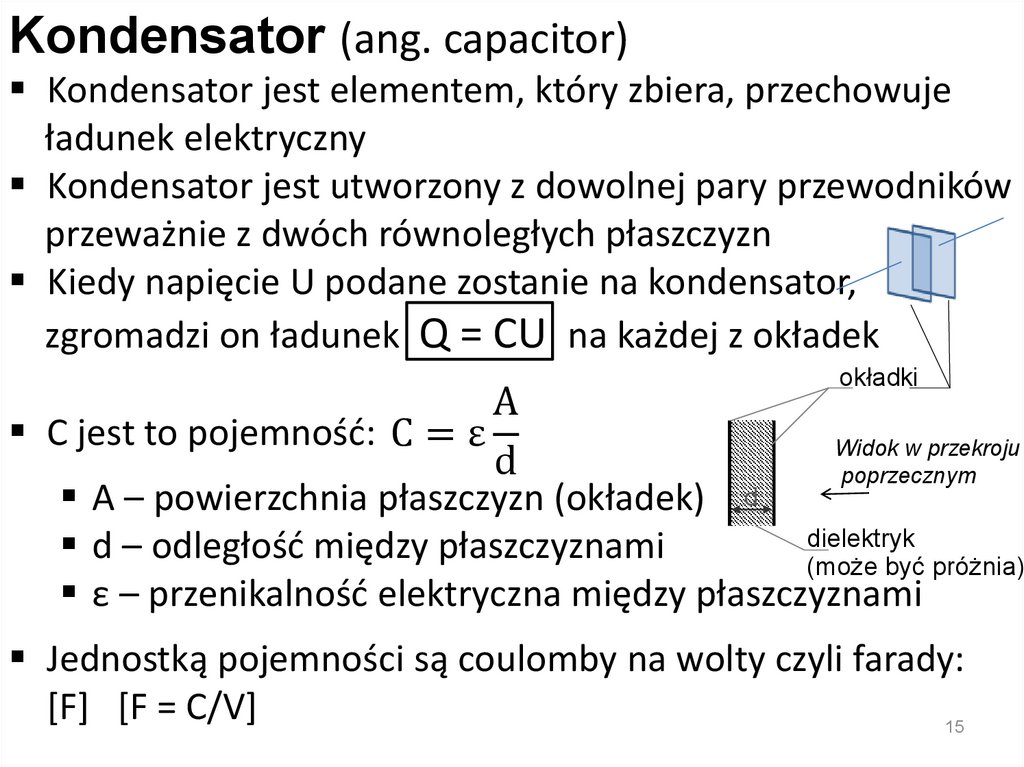
Kondensator (ang. capacitor)Kondensator jest elementem, który zbiera, przechowuje
ładunek elektryczny
Kondensator jest utworzony z dowolnej pary przewodników
przeważnie z dwóch równoległych płaszczyzn
Kiedy napięcie U podane zostanie na kondensator,
zgromadzi on ładunek Q = CU na każdej z okładek
okładki
A
C jest to pojemność: C = ε
Widok w przekroju
d
poprzecznym
A – powierzchnia płaszczyzn (okładek) d
dielektryk
d – odległość między płaszczyznami
(może być próżnia)
ε – przenikalność elektryczna między płaszczyznami
Jednostką pojemności są coulomby na wolty czyli farady:
[F] [F = C/V]
15
16.
KondensatorTypowe wartości pojemności kondensatorów mieszczą się
w zakresie od pF do μF
Napięcie przebicia kondensatora jest maksymalnym
napięciem przy którym może pracować. Powyżej tego
napięcia następuje przebicie elektryczne dielektryka
dQ
Z definicji prądu: i =
więc natężenie prądu
dt
płynącego przez kondensator wynosi:
du
i=C
dt
Uwaga: w definicji wielką literą Q oznaczyliśmy ładunek zmienny w czasie
16
17.
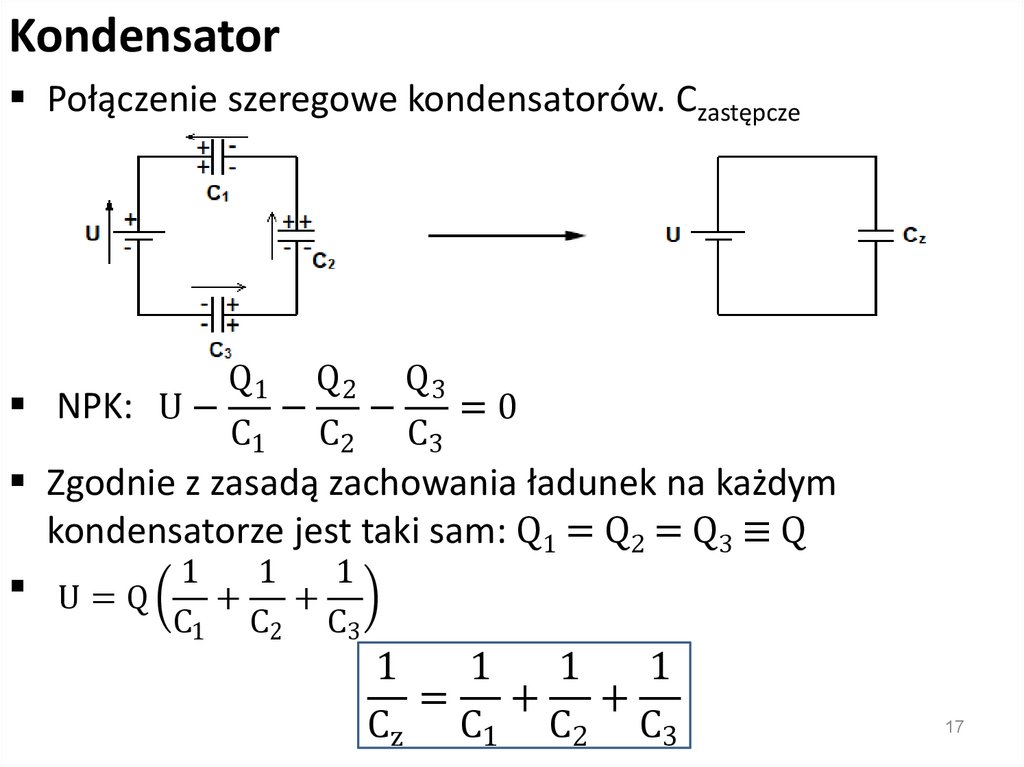
KondensatorPołączenie szeregowe kondensatorów. Czastępcze
Q1 Q 2 Q 3
NPK: U − −
−
=0
C1 C2 C3
Zgodnie z zasadą zachowania ładunek na każdym
kondensatorze jest taki sam: Q1 = Q2 = Q3 ≡ Q
U=Q 1 + 1 + 1
C1
C2
C3
1
1
1
1
= + +
Cz C1 C2 C3
17
18.
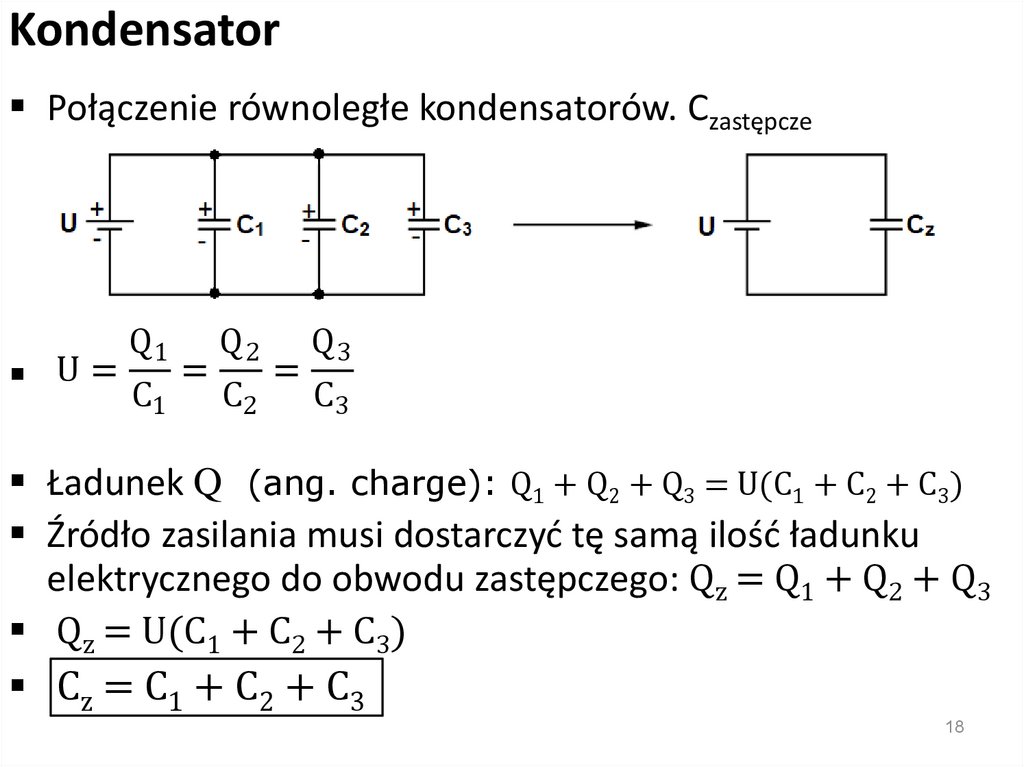
KondensatorPołączenie równoległe kondensatorów. Czastępcze
Q1 Q 2 Q 3
U=C =C =C
1
2
3
Ładunek Q (ang. charge): Q1 + Q2 + Q3 = U(C1 + C2 + C3)
Źródło zasilania musi dostarczyć tę samą ilość ładunku
elektrycznego do obwodu zastępczego: Qz = Q1 + Q2 + Q3
Qz = U(C1 + C2 + C3)
Cz = C 1 + C 2 + C 3
18
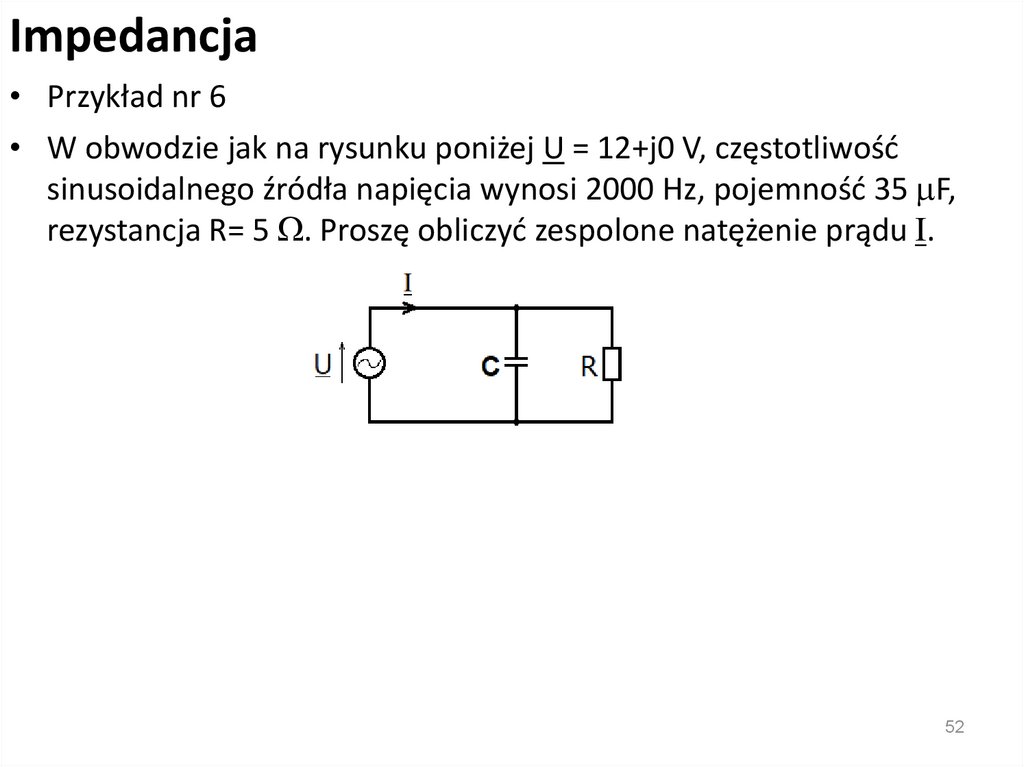
19.
KondensatorPrzykład nr 1
Proszę obliczyć pojemność Cz poniższego obwodu
CZ
• C34= C3 + C4 = 100·10-6 + 10·10-6 = 110·10-6
1/CZ = 1/C1 + 1/C2 + 1/C34 = 1/2.7*10-6 + 1/2.7·10-6 + 1/110·10-6
1/CZ = 0.37·106 + 0.37·106 + 0.009·106 = 0.749·106
CZ = 1/0.749·106 = 1.335·10-6
CZ = 1.335 mF - wynik
19
20.
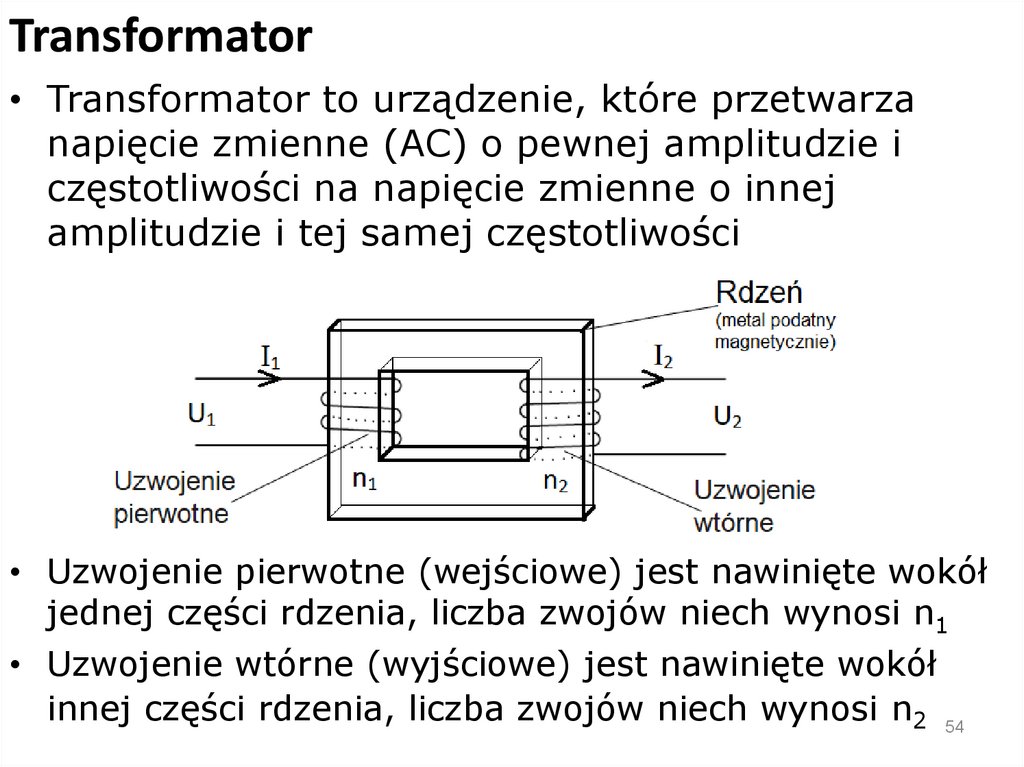
Cewka (ang. inductor)di
Prąd i zmienny w czasie indukuje napięcie: u=L
dt
L jest nazywana samoindukcyjnością lub indukcyjnością
Dowolna pętla obwodu posiada indukcję, którą zazwyczaj
pomijamy podobnie jak pomijamy małą rezystancję kabli i
połączeń elektrycznych
Jeśli w obwodzie potrzebna jest indukcyjność, umieszczony
zostaje element dyskretny
zwój
rdzeń
2R
μ – przenikalność magnetyczna rdzenia, na którym nawinięta
jest cewka, N – liczba zwojów przewodnika, R – promień
cewki, l – długość zwoju
Jednostką indukcyjności jest volt razy sekunda na amper, czyli
Henr [H] = V s/A
20
21.
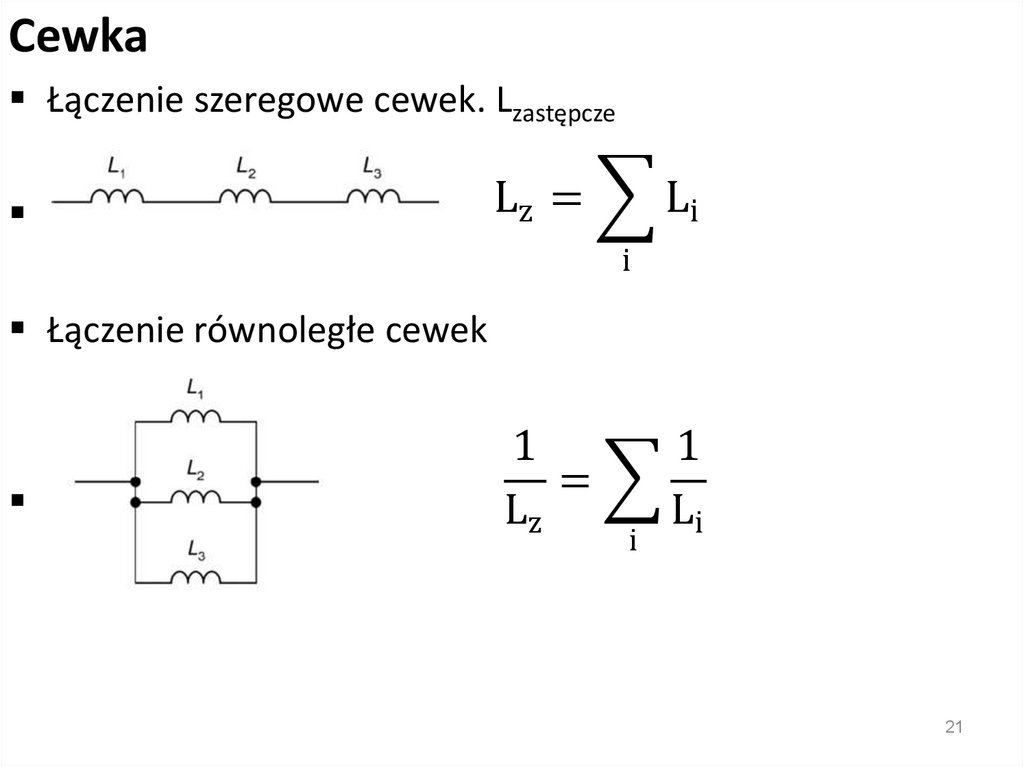
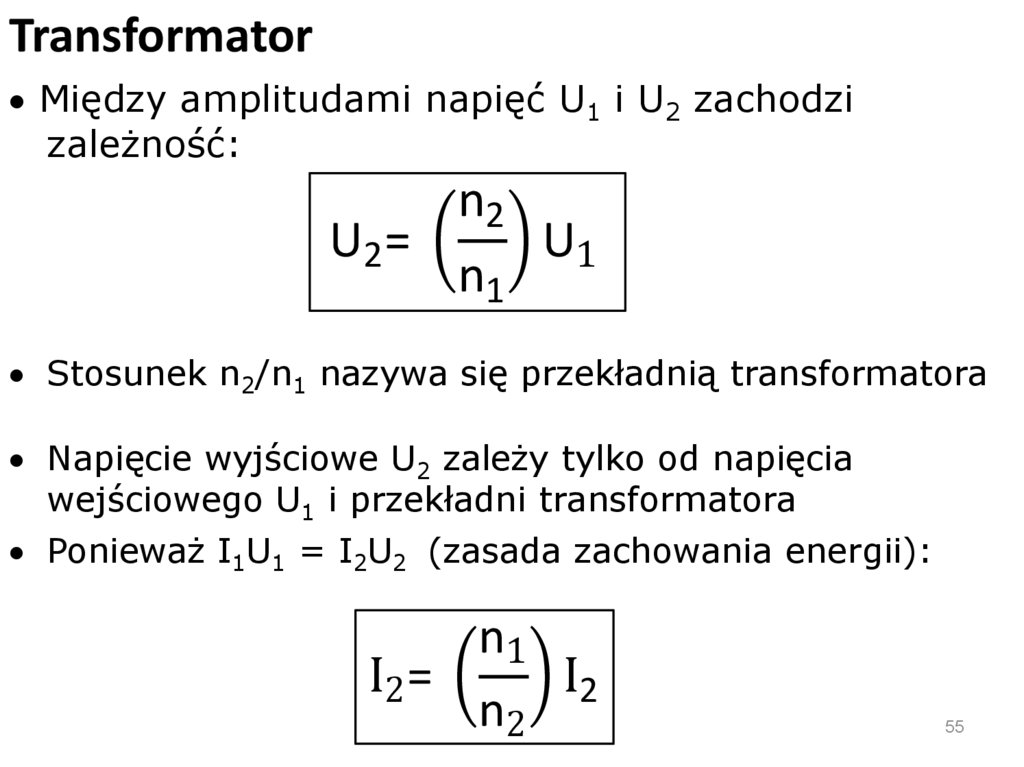
CewkaŁączenie szeregowe cewek. Lzastępcze
Lz =
Li = L1 + L2 + L3
i
Łączenie równoległe cewek
1
=
Lz
i
1
1
1
1
=
+ +
Li
L1 L2 L3
21
22.
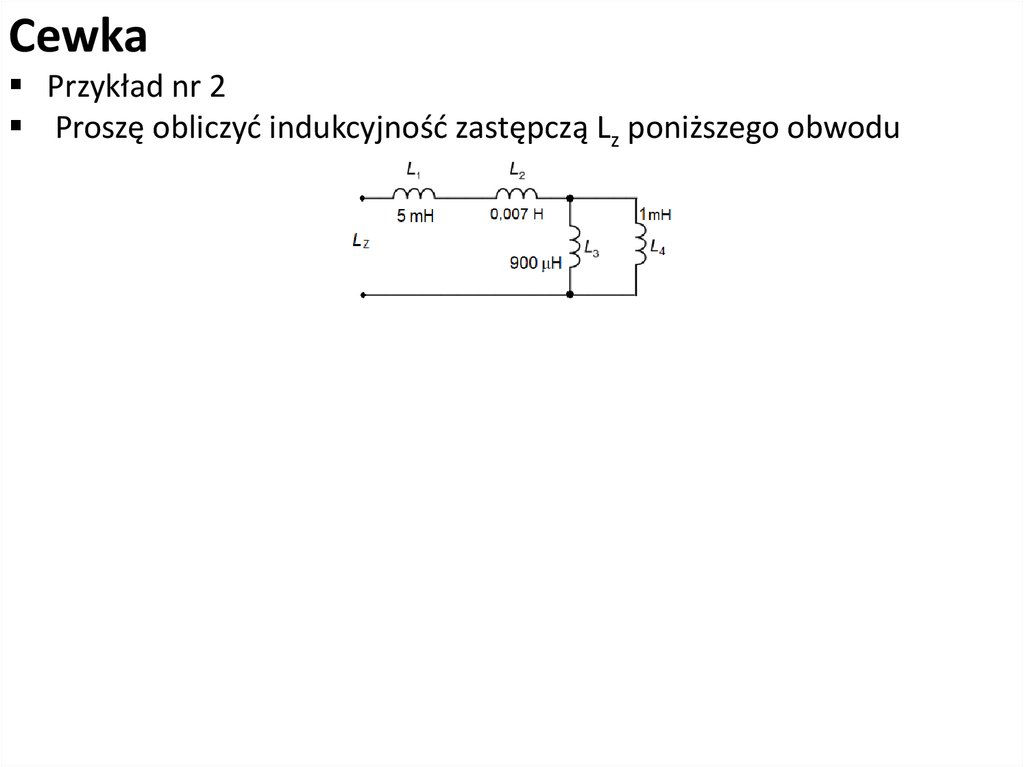
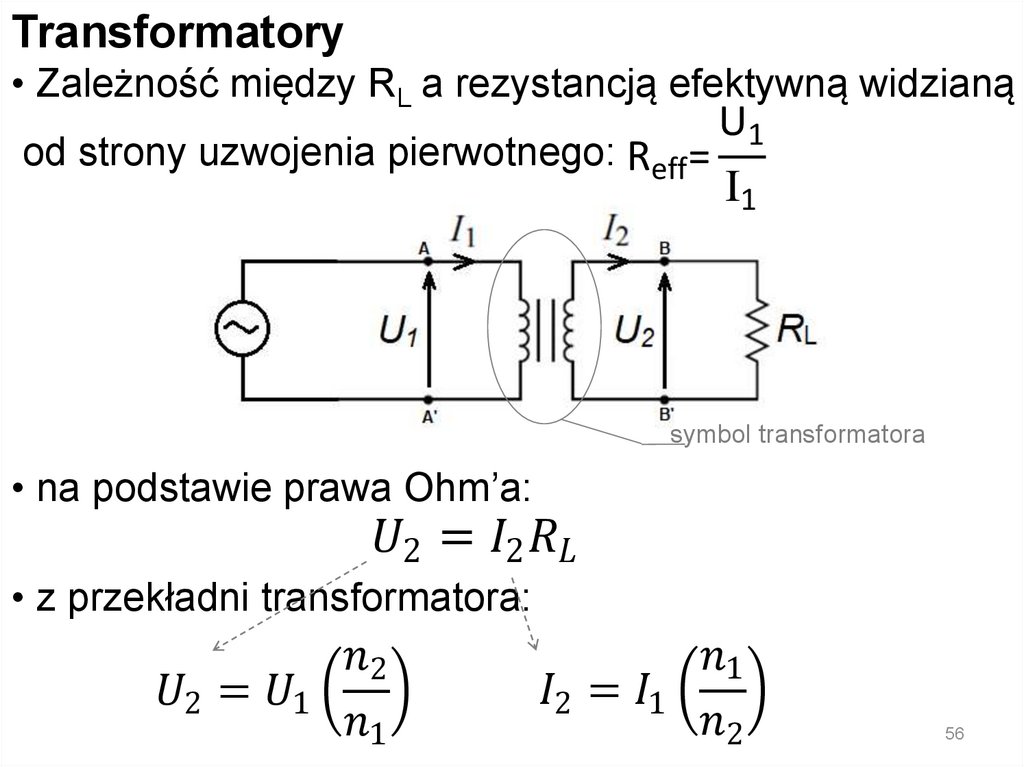
CewkaPrzykład nr 2
Proszę obliczyć indukcyjność zastępczą Lz poniższego obwodu
L12 = L1 + L2 = 5 10-3 + 7 10-3 = 12 10-3
1 1 1
1
1
1
1
3
3
3
= + =
+
=
+
=
1,11 10
+
10
=
2,11 10
L34 L3 L4 900 10-6 1 10-3 0,9 10-3 10-3
1
-3
L34 =
=0,474 10
2,11 103
LZ = L12 + L34 = 12 10-3 + 0,474 10-3 = 12,474 10-3
LZ = 12,474 mH
22
23.
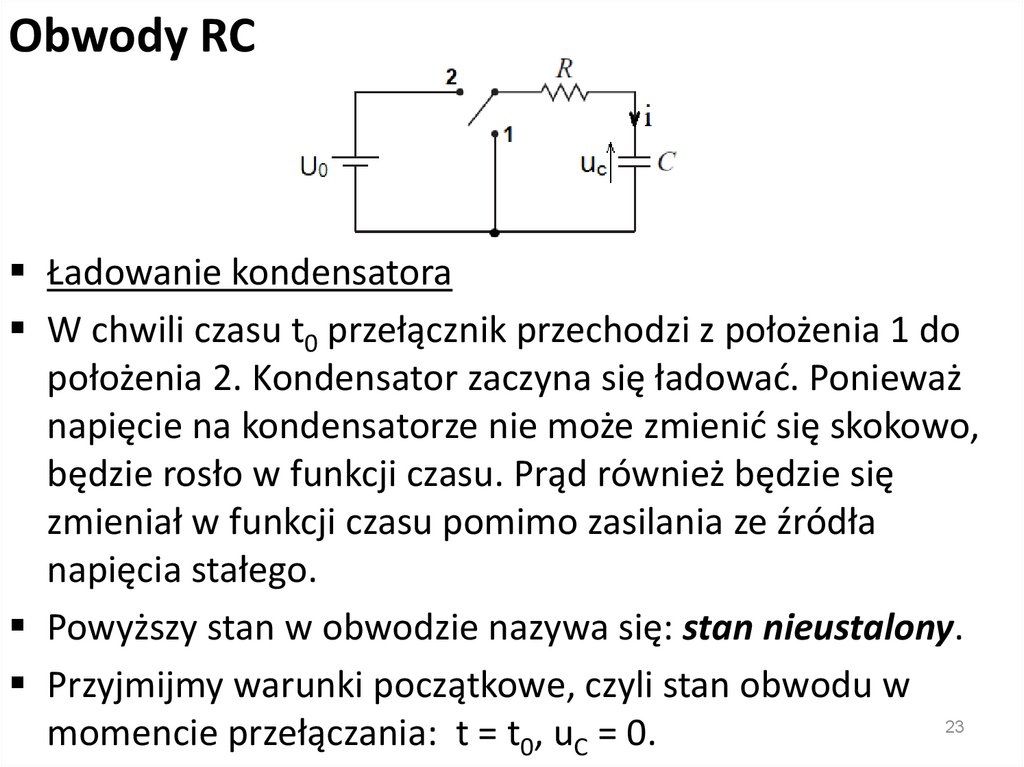
Obwody RCŁadowanie kondensatora
W chwili czasu t0 przełącznik przechodzi z położenia 1 do
położenia 2. Kondensator zaczyna się ładować. Ponieważ
napięcie na kondensatorze nie może zmienić się skokowo,
będzie rosło w funkcji czasu. Prąd również będzie się
zmieniał w funkcji czasu pomimo zasilania ze źródła
napięcia stałego.
Powyższy stan w obwodzie nazywa się: stan nieustalony.
Przyjmijmy warunki początkowe, czyli stan obwodu w
23
momencie przełączania: t = t0, uC = 0.
24.
Obwody RC – ładowanie kondensatoraPrąd płynący w obwodzie w funkcji czasu:
U0
t
i =
exp –
R
RC
Napięcie na kondensatorze w funkcji czasu
t
uc = U0 1 – exp –
RC
exp(x) = ex
e- liczba Eulera
e = 2,718…..
24
25.
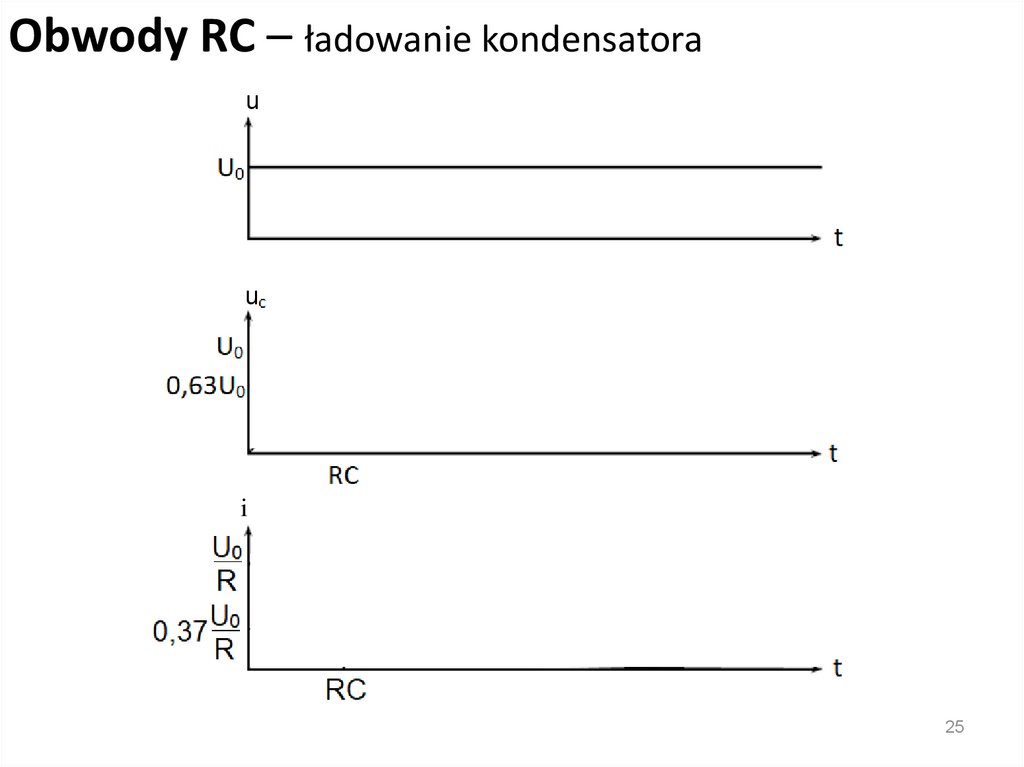
Obwody RC – ładowanie kondensatorau
u
i
25
26.
Obwody RC – ładowanie kondensatoraPrzebieg eksponenty zależy od stosunku t/RC
Iloczyn RC ma jednostki czasu, jest nazywany stałą czasową
zanikania
Stała czasowa RC często jest oznaczana grecką literą t
t decyduje o tym jak długo obwód dochodzi do stanu
ustalonego
Kiedy minie czas t = RC, prąd spada do około 37% wartości
początkowej a kondensator uzyskuje około 63% napięcia
pełnego naładowania (stanu ustalonego)
Większy kondensator potrzebuje więcej czasu aby się
naładować, większy rezystor ogranicza szybkość przepływu
ładunku (natężenie prądu) i wydłuża czas ładowania
26
27.
Obwody RC – ładowanie kondensatoraPo czasie t = 5t czyli kiedy minie 5 stałych czasowych od
momentu przełączenia prąd i napięcie zmieniają się już
bardzo mało
Mówimy że obwód RC doszedł do stanu ustalonego.
27
28.
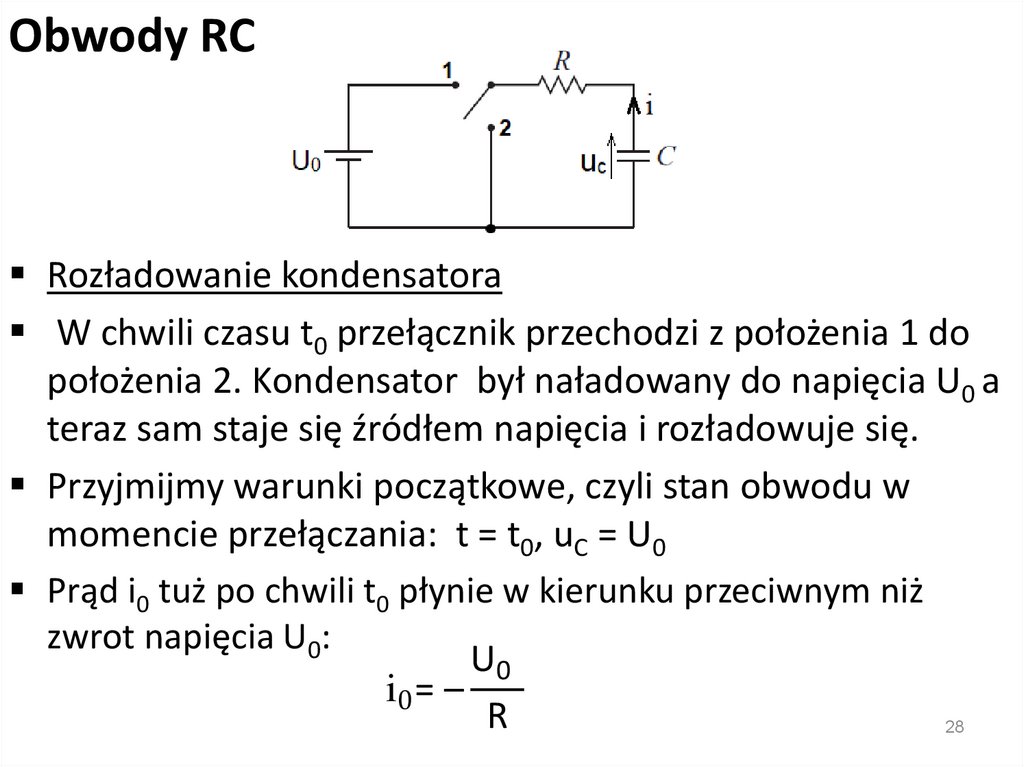
Obwody RCRozładowanie kondensatora
W chwili czasu t0 przełącznik przechodzi z położenia 1 do
położenia 2. Kondensator był naładowany do napięcia U0 a
teraz sam staje się źródłem napięcia i rozładowuje się.
Przyjmijmy warunki początkowe, czyli stan obwodu w
momencie przełączania: t = t0, uC = U0
Prąd i0 tuż po chwili t0 płynie w kierunku przeciwnym niż
zwrot napięcia U0:
U0
i0 = –
R
28
29.
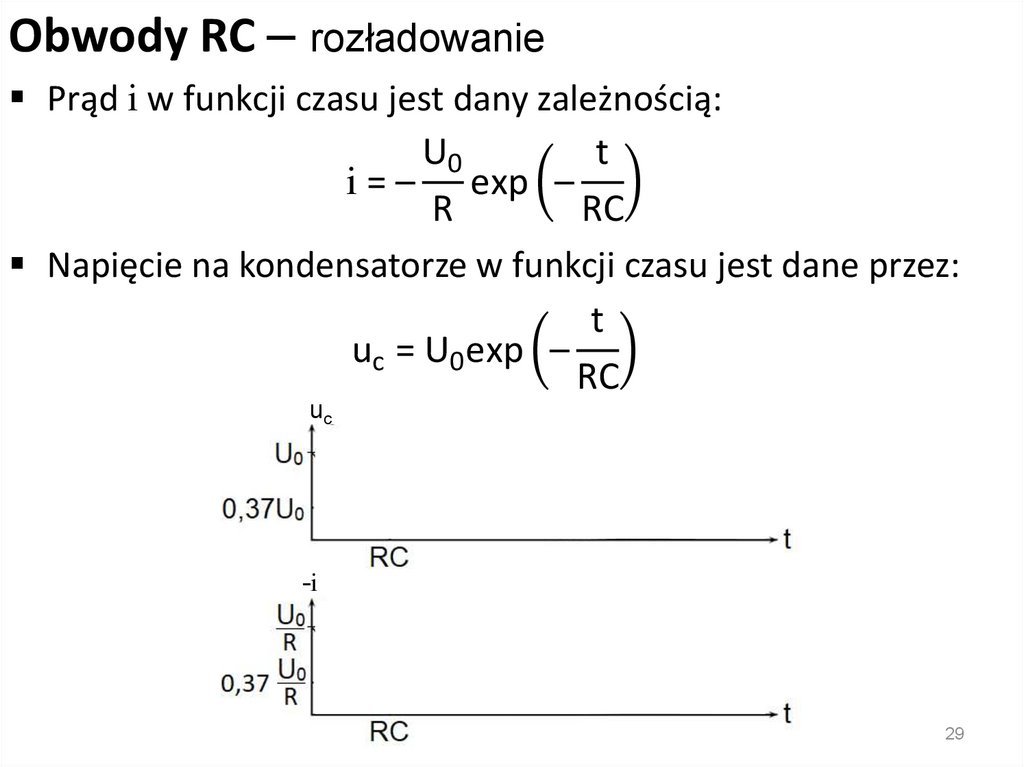
Obwody RC – rozładowaniePrąd i w funkcji czasu jest dany zależnością:
U0
t
i = – exp –
R
RC
Napięcie na kondensatorze w funkcji czasu jest dane przez:
t
uc = U0 exp –
RC
uc
-i
29
30.
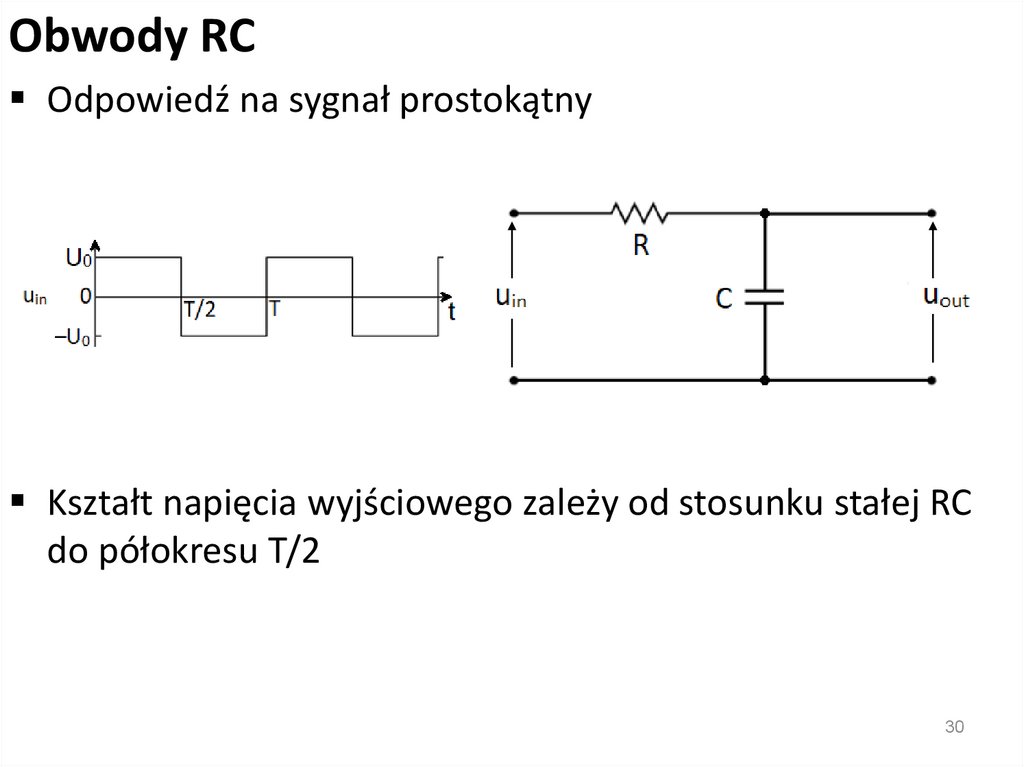
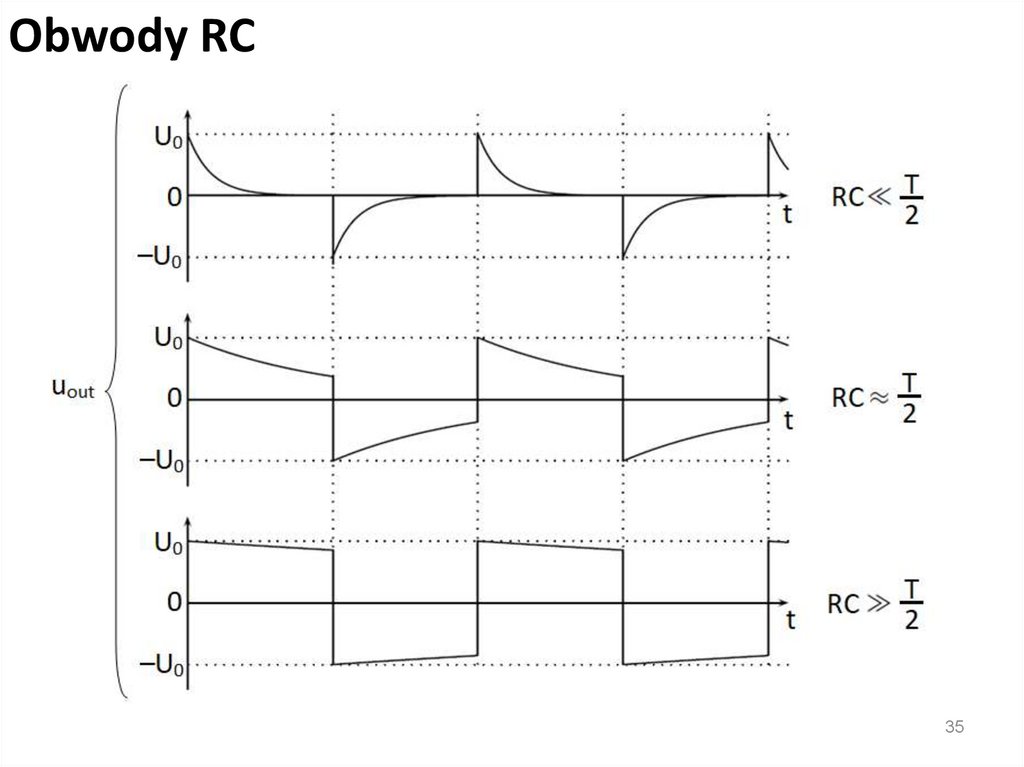
Obwody RCOdpowiedź na sygnał prostokątny
Kształt napięcia wyjściowego zależy od stosunku stałej RC
do półokresu T/2
30
31.
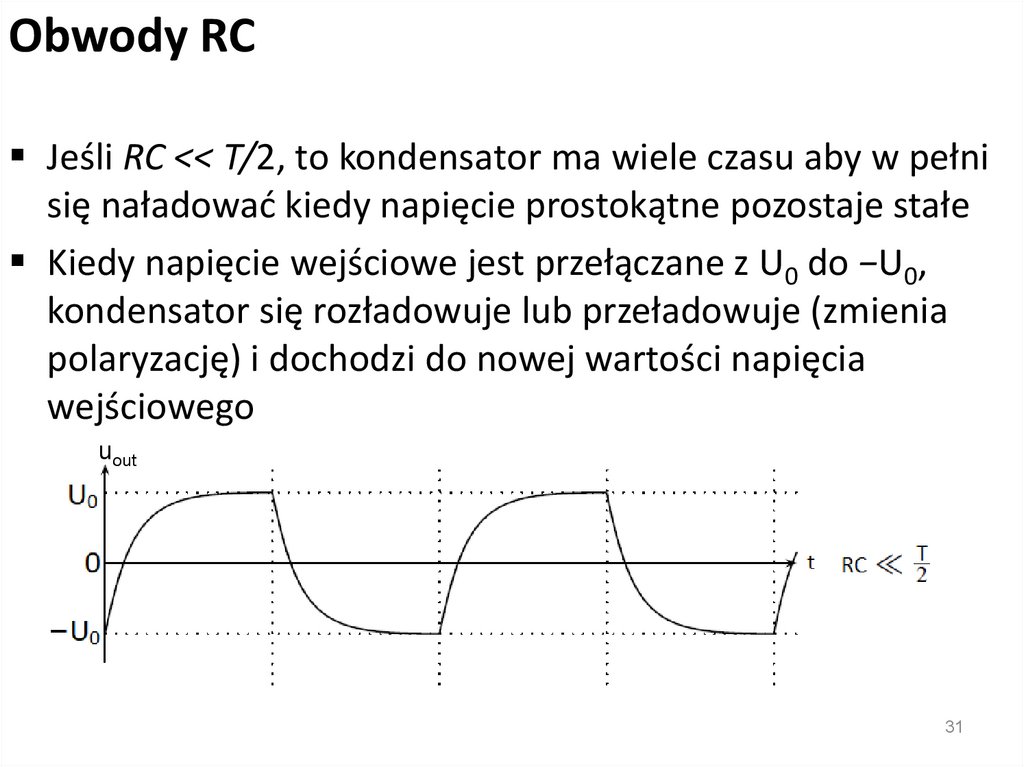
Obwody RCJeśli RC << T/2, to kondensator ma wiele czasu aby w pełni
się naładować kiedy napięcie prostokątne pozostaje stałe
Kiedy napięcie wejściowe jest przełączane z U0 do −U0,
kondensator się rozładowuje lub przeładowuje (zmienia
polaryzację) i dochodzi do nowej wartości napięcia
wejściowego
uout
31
32.
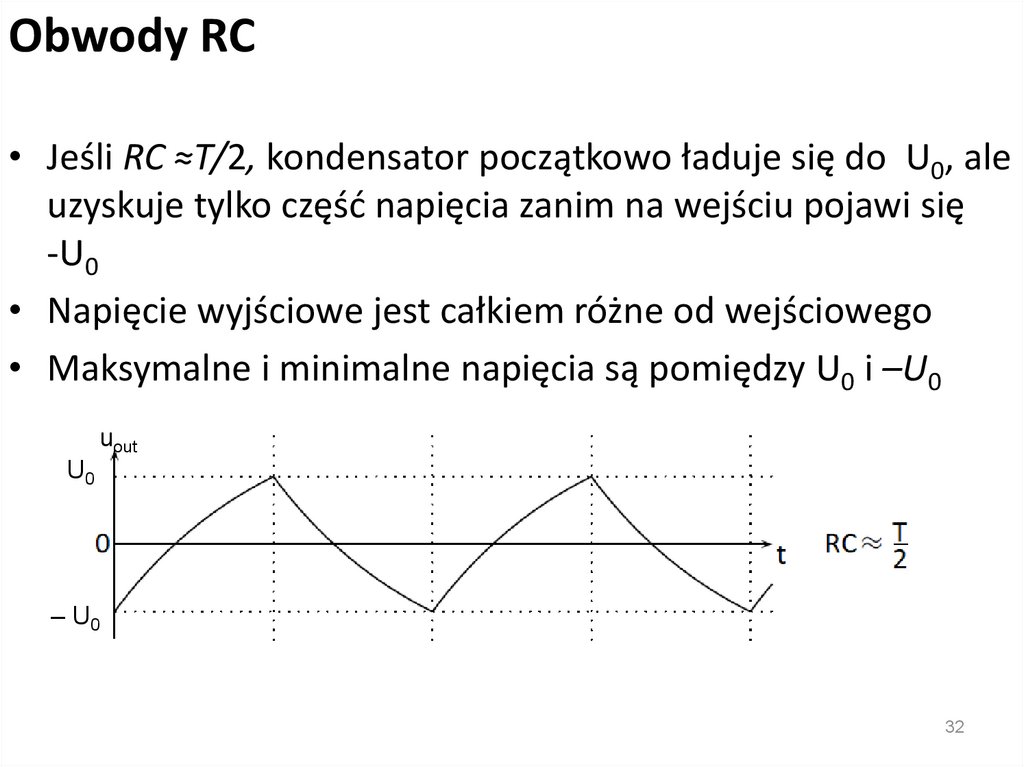
Obwody RC• Jeśli RC ≈T/2, kondensator początkowo ładuje się do U0, ale
uzyskuje tylko część napięcia zanim na wejściu pojawi się
-U0
• Napięcie wyjściowe jest całkiem różne od wejściowego
• Maksymalne i minimalne napięcia są pomiędzy U0 i –U0
uout
U0
– U0
32
33.
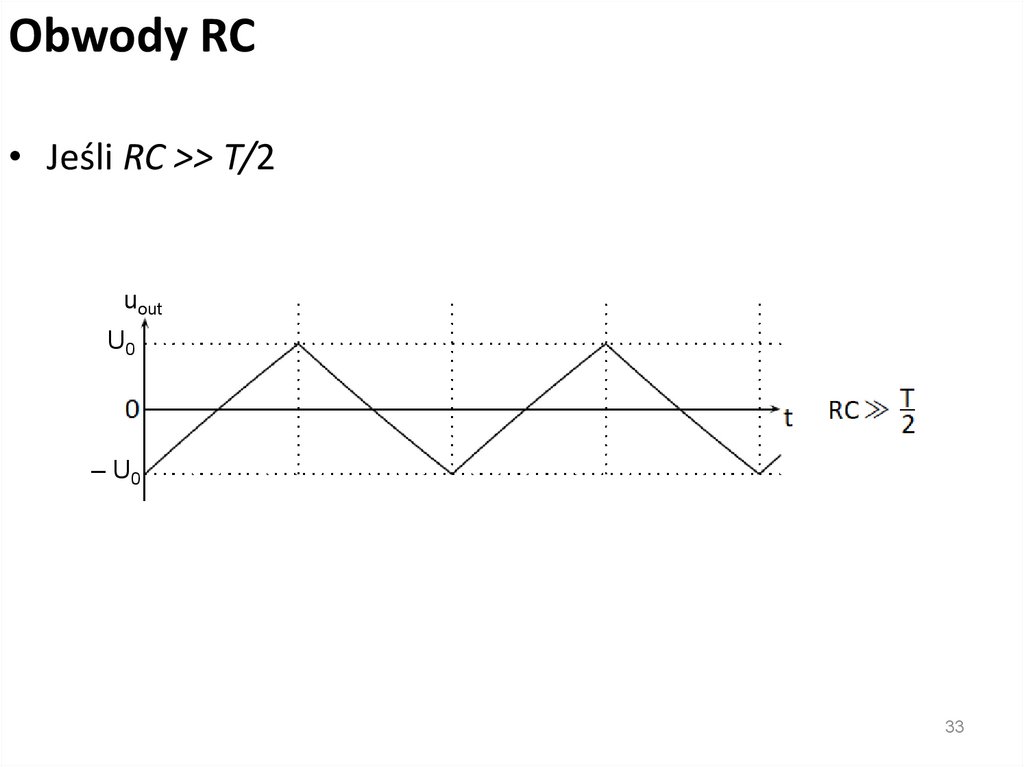
Obwody RC• Jeśli RC >> T/2
uout
U0
– U0
33
34.
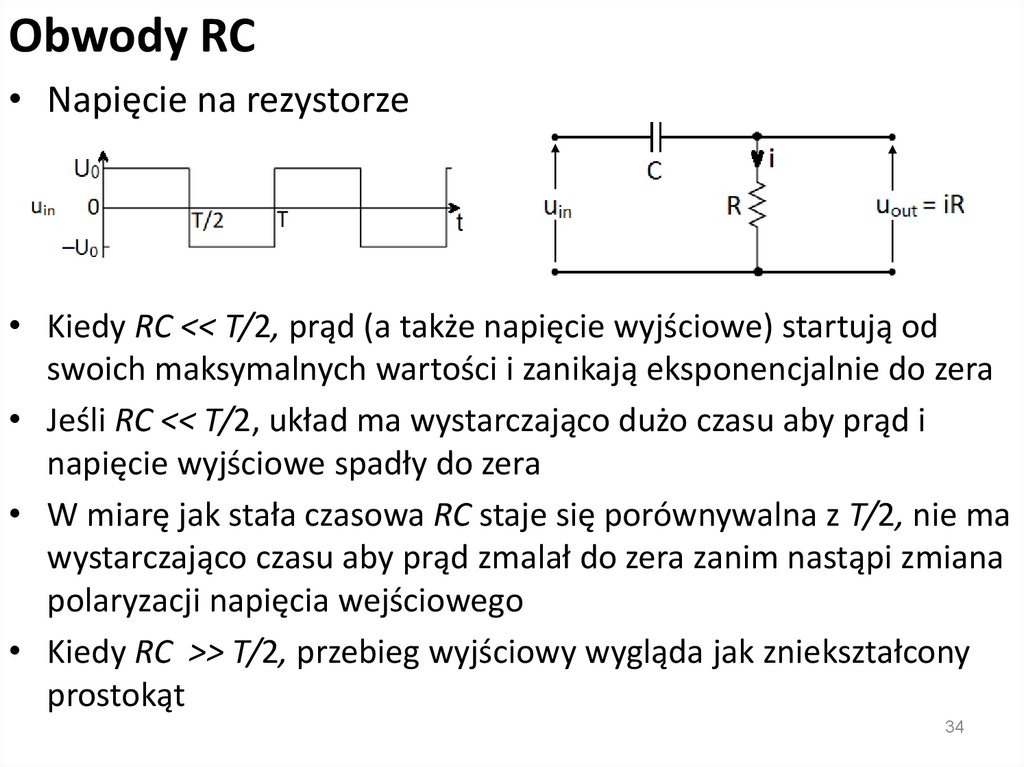
Obwody RC• Napięcie na rezystorze
• Kiedy RC << T/2, prąd (a także napięcie wyjściowe) startują od
swoich maksymalnych wartości i zanikają eksponencjalnie do zera
• Jeśli RC << T/2, układ ma wystarczająco dużo czasu aby prąd i
napięcie wyjściowe spadły do zera
• W miarę jak stała czasowa RC staje się porównywalna z T/2, nie ma
wystarczająco czasu aby prąd zmalał do zera zanim nastąpi zmiana
polaryzacji napięcia wejściowego
• Kiedy RC >> T/2, przebieg wyjściowy wygląda jak zniekształcony
prostokąt
34
35.
Obwody RC35
36.
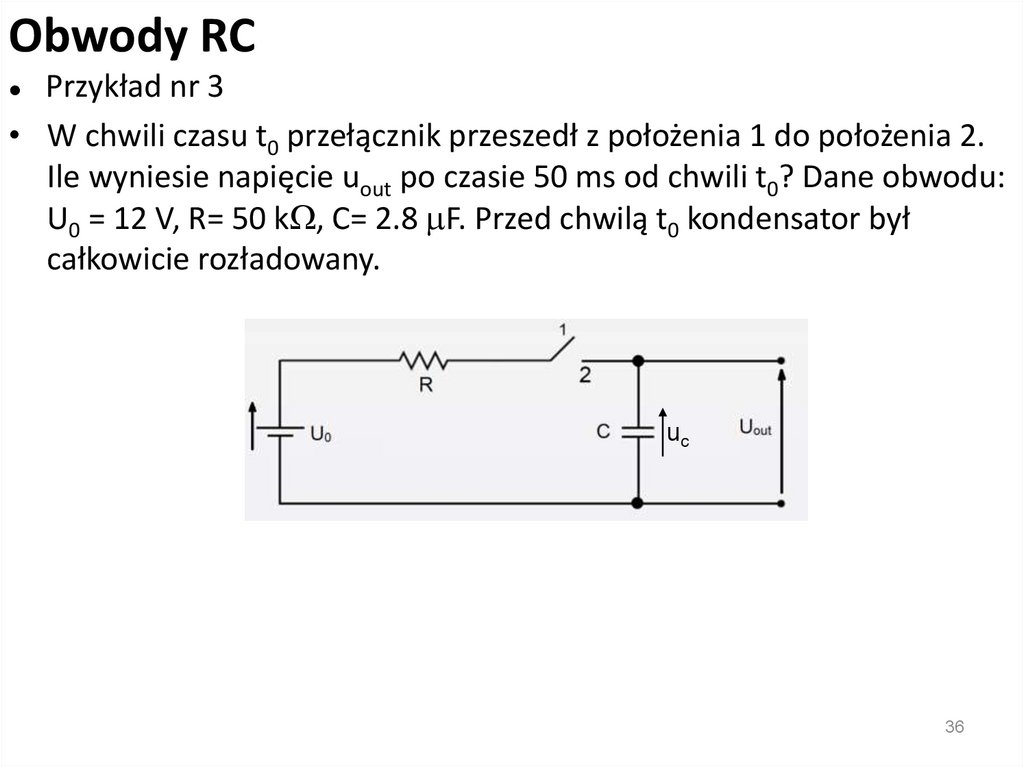
Obwody RCPrzykład nr 3
• W chwili czasu t0 przełącznik przeszedł z położenia 1 do położenia 2.
Ile wyniesie napięcie uout po czasie 50 ms od chwili t0? Dane obwodu:
U0 = 12 V, R= 50 kW, C= 2.8 mF. Przed chwilą t0 kondensator był
całkowicie rozładowany.
• uout=uc = U0·[1 – exp(-t/(RC))]
• uout= 12·[1 – exp(-50ms/(50kW·2.8mF))]
uc
• uout= 12·[1 – exp(-50·10–3/(50·103·2.8 10–6 ))]
• uout= 12·[1 – exp(-50·10–3/(140·10–3 ))]
• uout= 12·[1 – exp(-0.357143)]
• uout= 12·(1 – 0.7)
• uout= 3.6 V - wynik
36
37.
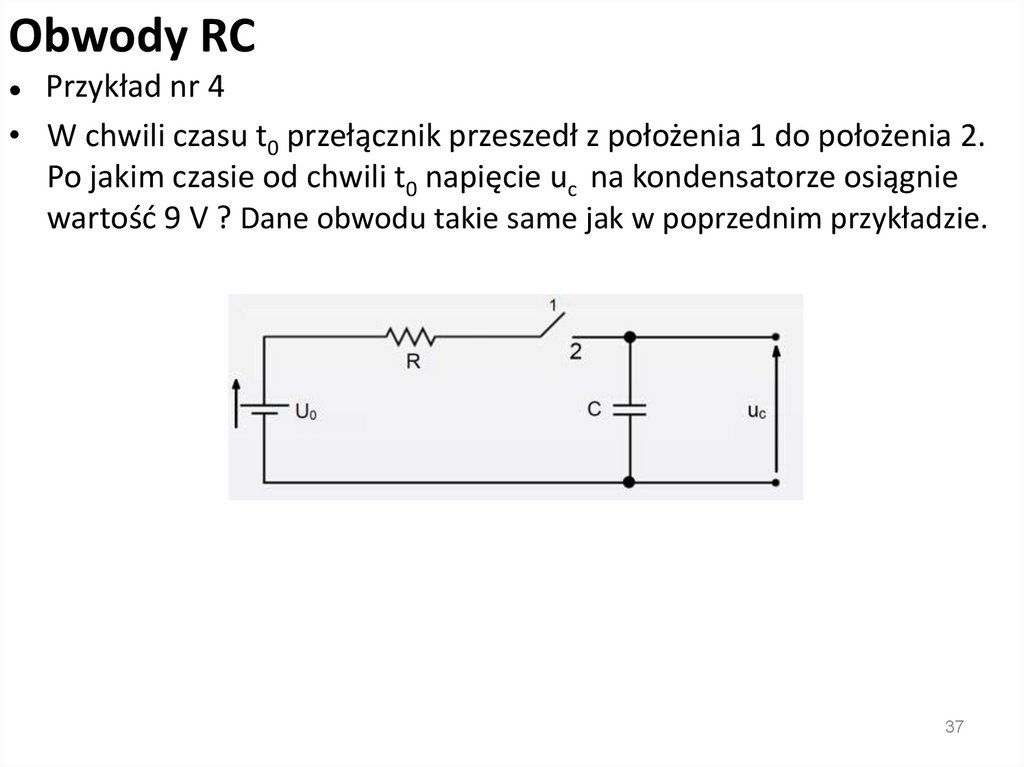
Obwody RCPrzykład nr 4
W chwili czasu t0 przełącznik przeszedł z położenia 1 do położenia 2.
Po jakim czasie od chwili t0 napięcie uc na kondensatorze osiągnie
wartość 9 V ? Dane obwodu takie same jak w poprzednim przykładzie.
uc = U0·[1 – exp(-t/RC)]
uc = U0 – U0· exp(-t/RC)
U0· exp(-t/RC) = U0 - uc /:U0
e(-t/RC) = (U0 - uc)/U0 / ln
ln e(-t/RC) = ln[(U0 - uc)/U0 ]
(-t/RC)·ln e = ln[(U0 - uc)/U0 ]
{ ln e =1 }
-t/RC = ln[(U0 - uc)/U0 ] /·(-RC)
t = -RC· ln[(U0 - uc)/U0 ]
t= - 50·103·2.8·10-6·ln[(12 – 9)/12]
t= - 140·10-3·ln(0.25) = -0.14·(-1.386)
37
t = 0.19 s
38.
Liczby zespolone (complex numbers)• Rozważamy prąd sinusoidalnie zmienny w
czasie: i = IAsin(ωt + φ)
• Nie chcemy wykonywać przekształceń
matematycznych na sinusoidach lub szeregach
aby obliczyć amplitudy prądu w obwodzie
• Problem ten może być rozwiązany w łatwy
sposób za pomocą liczb zespolonych
• z = a + jb
(postać algebraiczna)
• gdzie a oraz b są liczbami rzeczywistymi
• natomiast j jest wielkością urojoną: j = –1
• Liczby zespolone oznaczamy przez podkreślenie
z lub przez daszek z
38
39.
Liczby zespolone• Czasami korzystnie jest przedstawić liczbę zespoloną
z jako wektor na płaszczyźnie zespolonej, gdzie oś
pionowa jest osią urojoną (imaginaire) związaną z
częścią urojoną Im(z), natomiast oś pozioma jest
osią rzeczywistą związaną z częścią rzeczywistą Re(z)
• Wektor może też być reprezentowany za pomocą
długości (modułu) |z| tego wektora oraz kąta między
tym wektorem a dodatnią osią rzeczywistą (poziomą) 39
40.
• Liczby zespolone• Postać algebraiczna liczby zespolonej
• z = a + jb
• a,b – liczby rzeczywiste;
• j – wielkość urojona
• j = –1
• j·j = – 1
• j·(– j)= 1
• (– j)·(– j) = – 1
• 1
= –j
• j
• Re(z) = a - składowa rzeczywista liczby zespolonej
• Im(z) = b - składowa urojona liczby zespolonej
40
41.
• Liczby zespolone• Postać trygonometryczna liczby zespolonej
• z = |z|(cos + jsin )
• gdzie:
• |z| = √ a2 + b2
-moduł
• moduł czasami oznaczany jest przez liczbę rzeczywistą: z
• = tan–1(b/a)
• tan–1(x) – funkcja odwrotna do tangensa (arcus tangens)
• czasami oznaczana jako arctg(x) lub atan(x)
41
42.
Liczby zespolone• Rozwinięcie Taylora dla sinusa i cosinusa:
• Postać wykładnicza liczby zespolonej:
z = |z|ej
• gdzie e jest to liczba Eulera: e = 2.7828…
42
43.
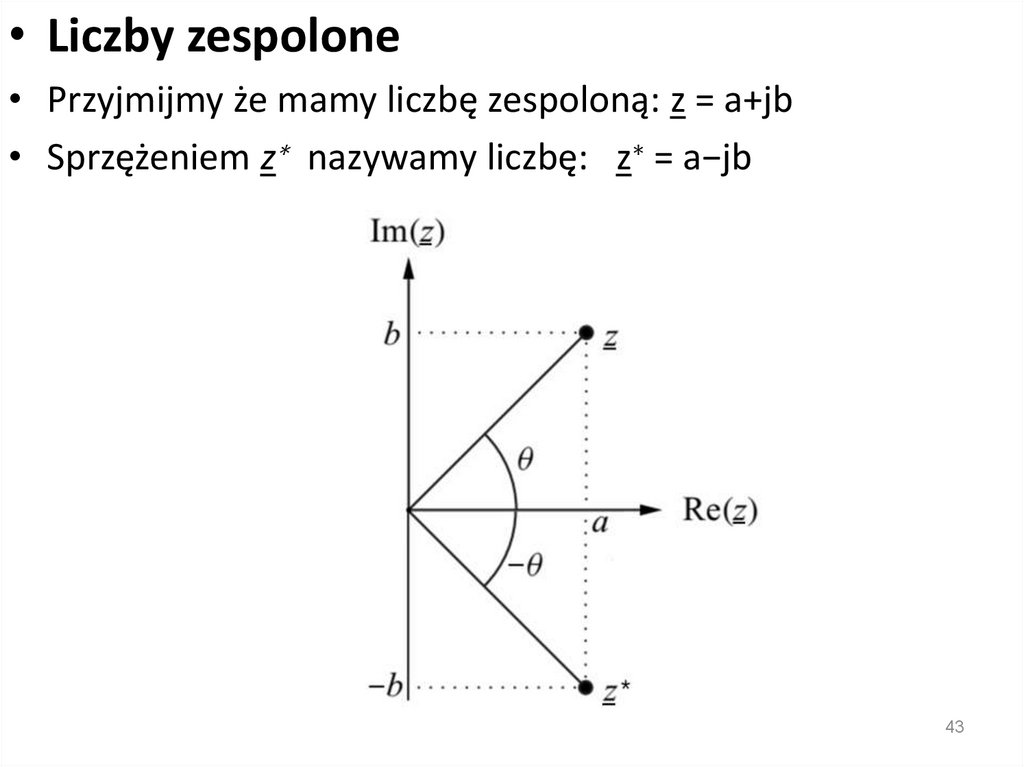
• Liczby zespolone• Przyjmijmy że mamy liczbę zespoloną: z = a+jb
• Sprzężeniem z∗ nazywamy liczbę: z∗ = a−jb
43
44.
• Liczby zespolone• W wyniku pomnożenia dowolnej liczby zespolonej przez jej
sprzężenie otrzymujemy kwadrat modułu:
• zz* = (a + jb)(a – jb) = a2 – j2b2 = a2 + b2 = |z|2
• Sprzężenie do liczby z = |z|ej w postaci wykładniczej:
• z* = |z|e−j
44
45.
• Liczby zespolone• Jeśli mamy dwie liczby zespolone z1 = a1 + jb1 i z2 = a2 + jb2 to
ich mnożenie jest dane wzorem:
• z1z2 = (a1 + jb1)(a2 + jb2) = (a1a2 – b1b2) + j(a1b2 + a2b1)
• a dzielenie jest dane wzorem:
45
46.
• Liczby zespolone• Jeśli mamy dwie liczby zespolone w postaci wykładniczej:
• z1 = |z1|ej 1 i z2 = |z2|ej 2 mnożenie jest dane wzorem:
• z1z2 = |z1|·|z2|ej( 1 + 2)
• dzielenie jest dane wzorem:
z1 |z1| j( 1 – 2)
• z =
e
|z2|
2
• Logarytm naturalny liczby z = |z|ej jest dany wzorem:
• Ln(z) = Ln(|z|) + j
• Kąt jest w tym przypadku w radianach
46
47.
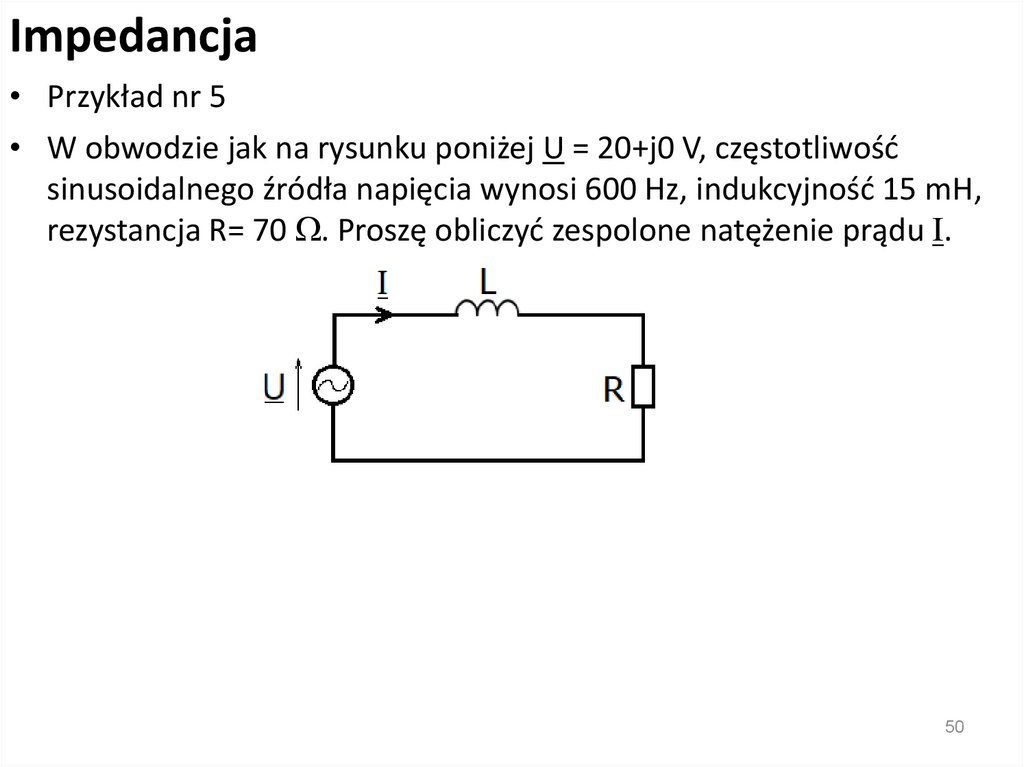
Impedancja• Liczby zespolone stosuje się do rozszerzenia prawa
Ohma
• Impedancja jest rozszerzeniem rezystancji, które ma
zastosowanie do rezystorów, kondensatorów i cewek
pracujących w obwodach prądu zmiennego
• Impedancja elementu obwodu jest liczbą zespoloną
• Jako symbolu impedancji używamy litery Z
47
48.
Impedancja• Impedancja ogranicza przepływ prądu, jest więc
uogólnioną rezystancją
• Dla kondensatorów i cewek impedancja jest
funkcją częstotliwości kołowej ω = 2pf
• Kiedy ω → 0, Zkondensatora → ∞ (kondensator dla prądu
stałego jest to przerwa w obwodzie)
• Kiedy ω → ∞, Zcewki → ∞ (cewka dla prądu zmiennego o
dużej częstotliwości jest to przerwa w obwodzie)
• Część rzeczywista zespolonej impedancji jest nazywana
impedancją rezystancyjną lub krótko: rezystancją.
• Część urojona jest nazywana impedancją reaktancyjną
lub krótko: reaktancją X (gdzie X= jX)
• Z = R + jX
48
49.
Impedancja• Zasady szeregowego i równoległego łączenia
impedancji są takie same jak dla rezystancji:

























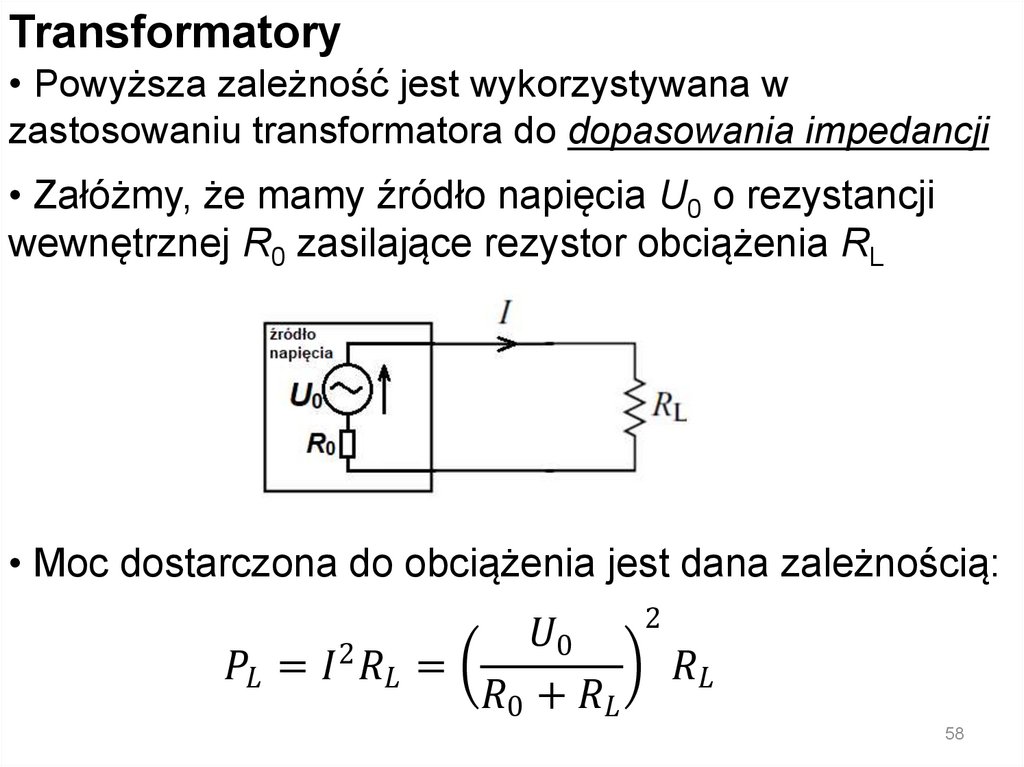


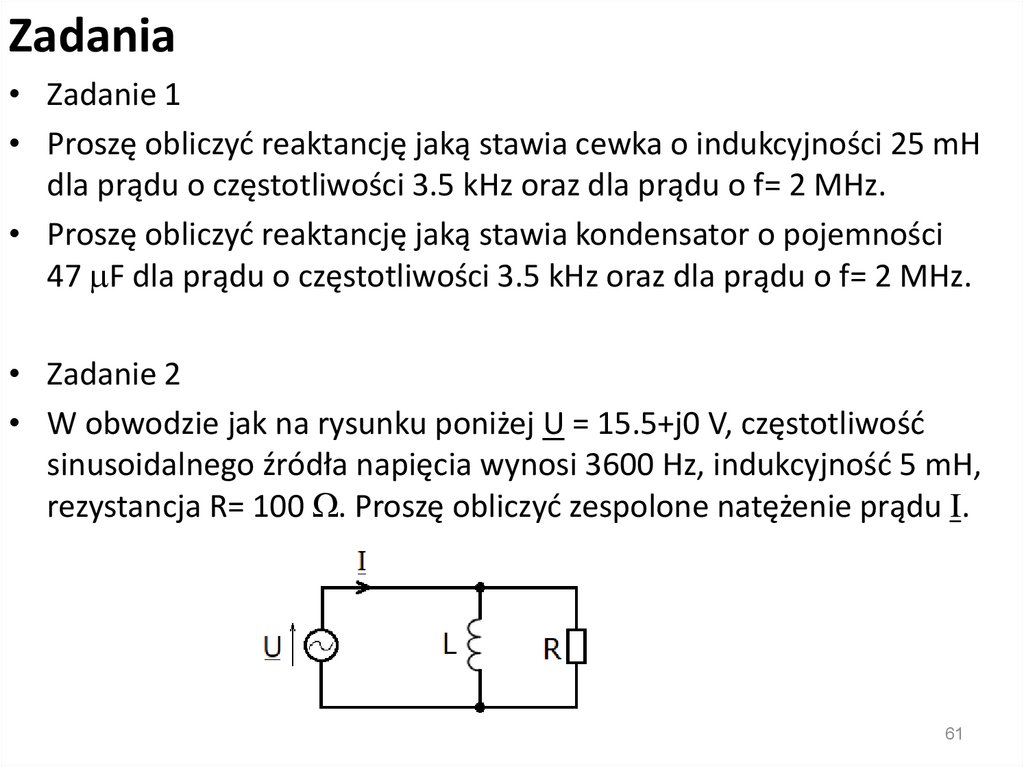

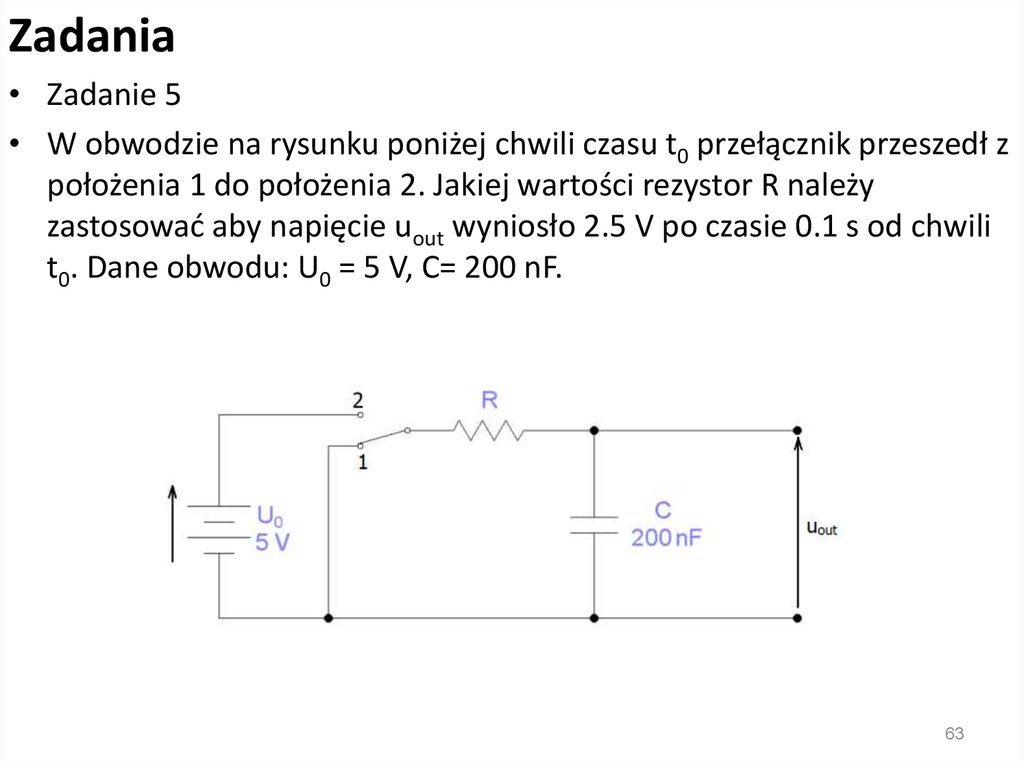

 electronics
electronics







