Similar presentations:
Комбинации многогранников и тел вращения
1.
2.
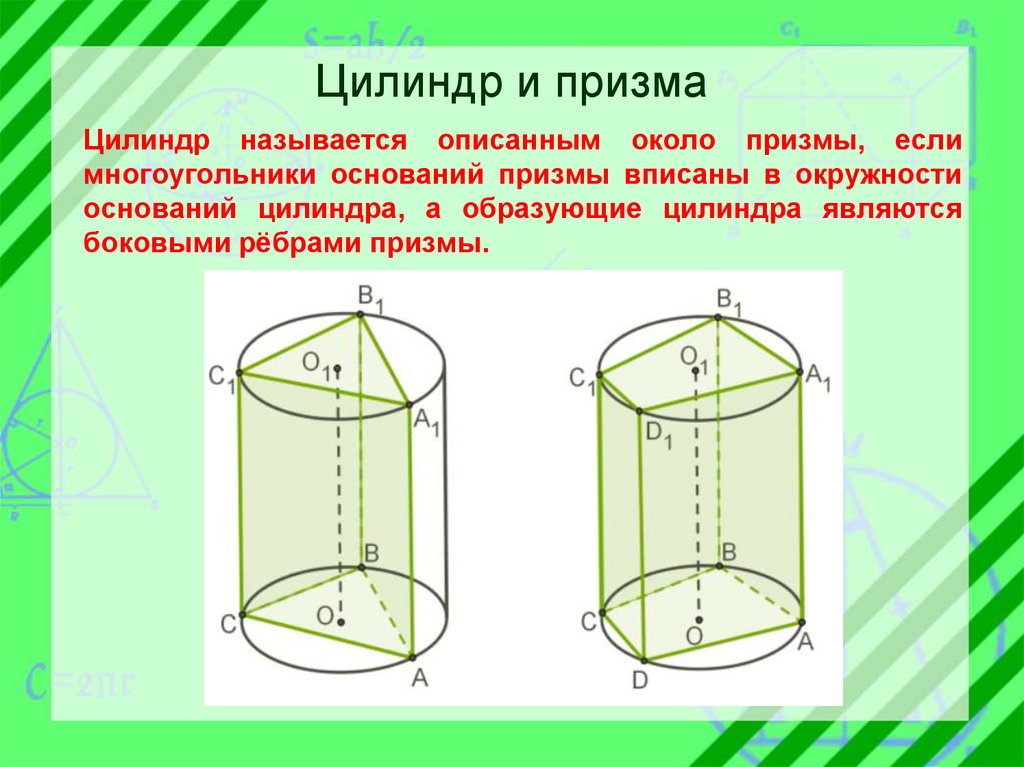
Цилиндр и призмаЦилиндр называется описанным около призмы, если
многоугольники оснований призмы вписаны в окружности
оснований цилиндра, а образующие цилиндра являются
боковыми рёбрами призмы.
3.
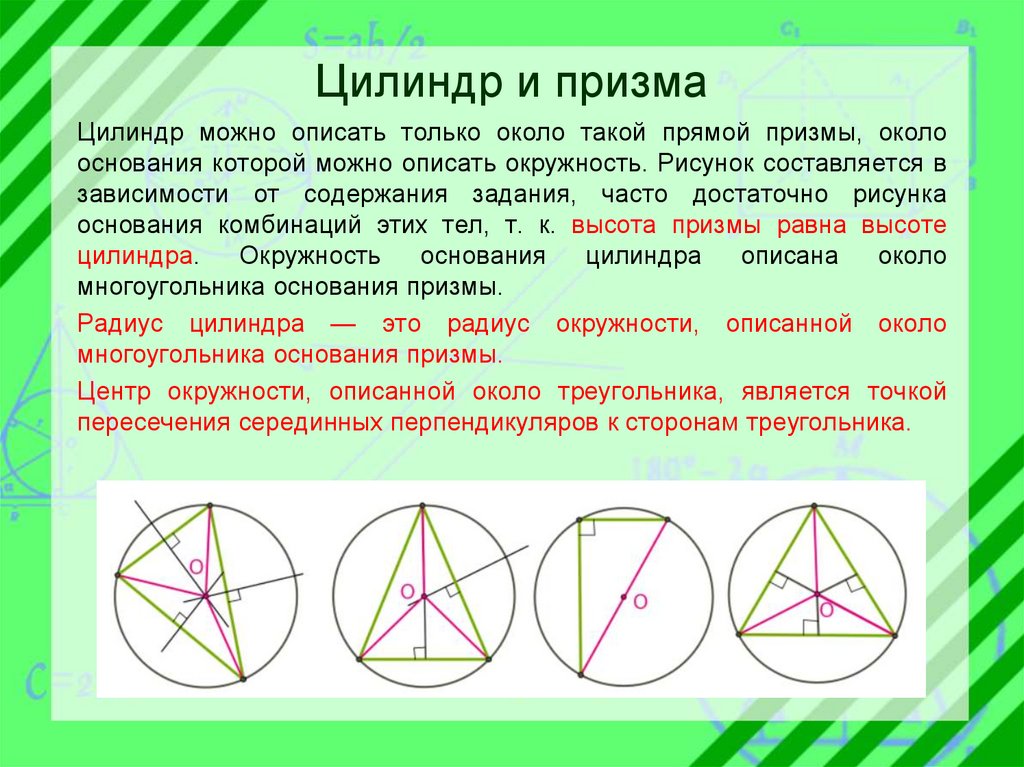
Цилиндр и призмаЦилиндр можно описать только около такой прямой призмы, около
основания которой можно описать окружность. Рисунок составляется в
зависимости от содержания задания, часто достаточно рисунка
основания комбинаций этих тел, т. к. высота призмы равна высоте
цилиндра.
Окружность
основания
цилиндра
описана
около
многоугольника основания призмы.
Радиус цилиндра — это радиус окружности, описанной около
многоугольника основания призмы.
Центр окружности, описанной около треугольника, является точкой
пересечения серединных перпендикуляров к сторонам треугольника.
4.
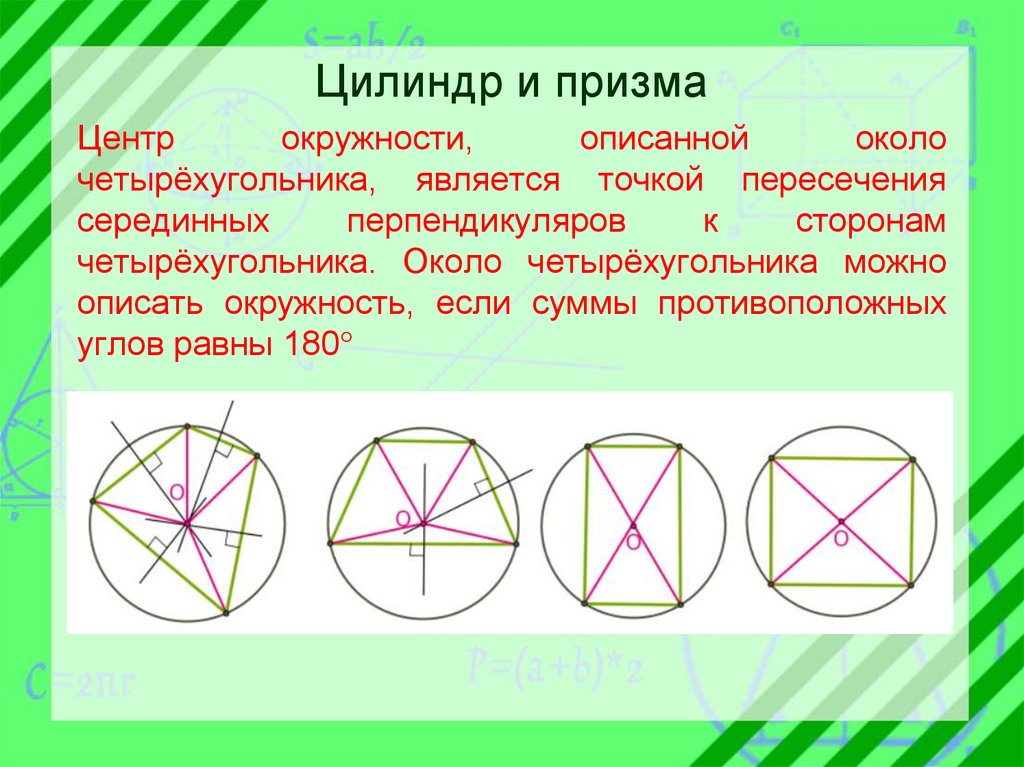
Цилиндр и призмаЦентр
окружности,
описанной
около
четырёхугольника, является точкой пересечения
серединных
перпендикуляров
к
сторонам
четырёхугольника. Около четырёхугольника можно
описать окружность, если суммы противоположных
углов равны 180
5.
6.
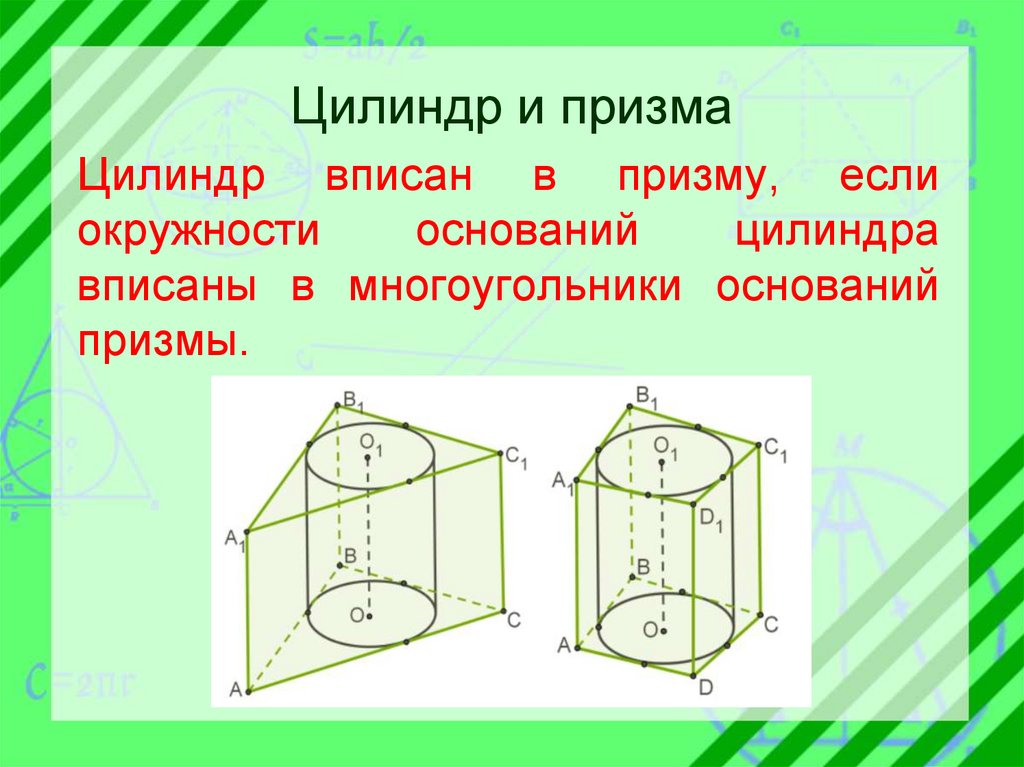
Цилиндр и призмаЦилиндр вписан в призму, если
окружности
оснований
цилиндра
вписаны в многоугольники оснований
призмы.
7.
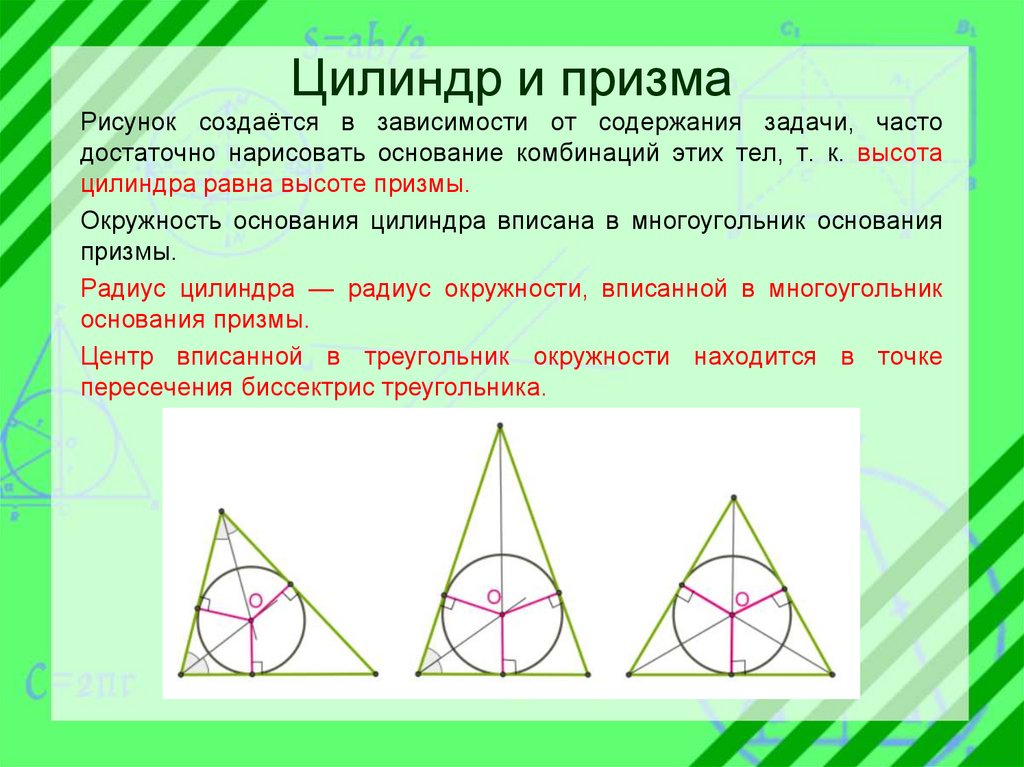
Цилиндр и призмаРисунок создаётся в зависимости от содержания задачи, часто
достаточно нарисовать основание комбинаций этих тел, т. к. высота
цилиндра равна высоте призмы.
Окружность основания цилиндра вписана в многоугольник основания
призмы.
Радиус цилиндра — радиус окружности, вписанной в многоугольник
основания призмы.
Центр вписанной в треугольник окружности находится в точке
пересечения биссектрис треугольника.
8.
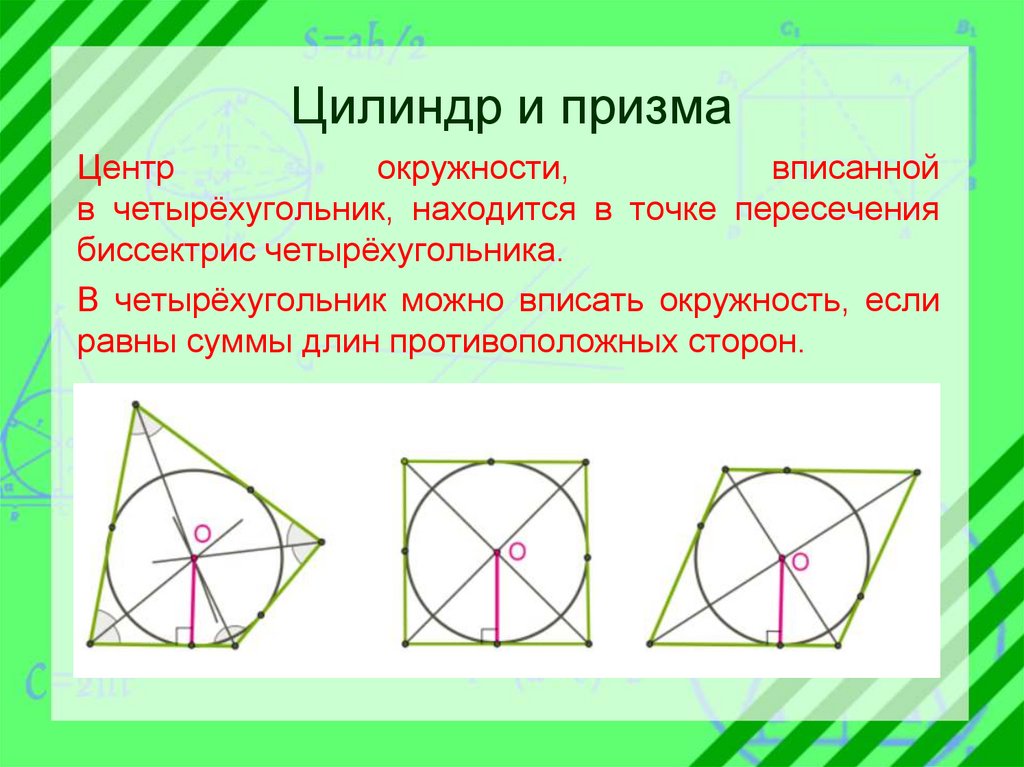
Цилиндр и призмаЦентр
окружности,
вписанной
в четырёхугольник, находится в точке пересечения
биссектрис четырёхугольника.
В четырёхугольник можно вписать окружность, если
равны суммы длин противоположных сторон.
9.
10.
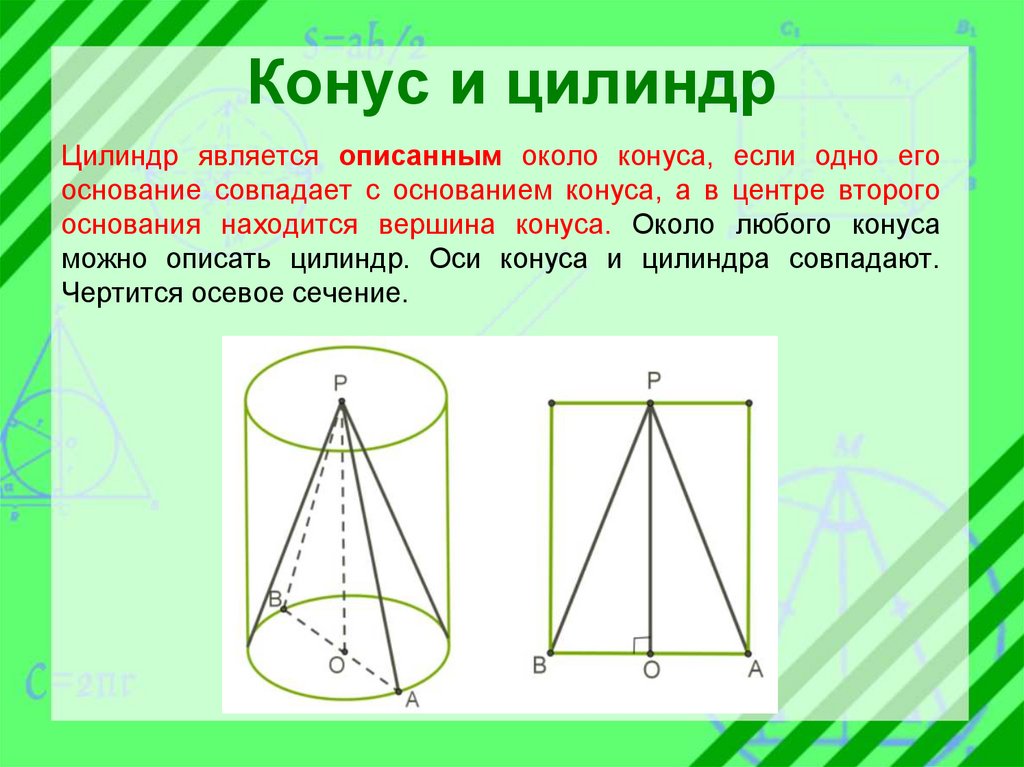
Конус и цилиндрЦилиндр является описанным около конуса, если одно его
основание совпадает с основанием конуса, а в центре второго
основания находится вершина конуса. Около любого конуса
можно описать цилиндр. Оси конуса и цилиндра совпадают.
Чертится осевое сечение.
11.
Конус и цилиндрЦилиндр является вписанным в конус, если одно его основание
находится в основании конуса, а второе основание касается всех
образующих конуса.
В любой конус можно вписать бесконечное множество цилиндров
(радиусы цилиндров меньше радиуса конуса).
Чертится осевое сечение. Центры оснований конуса и цилиндра
совпадают, а высота и радиусы различаются.
Чтобы определить зависимость между радиусами или
высотами конуса и цилиндра, в задаче должна присутствовать
дополнительная информация.
12.
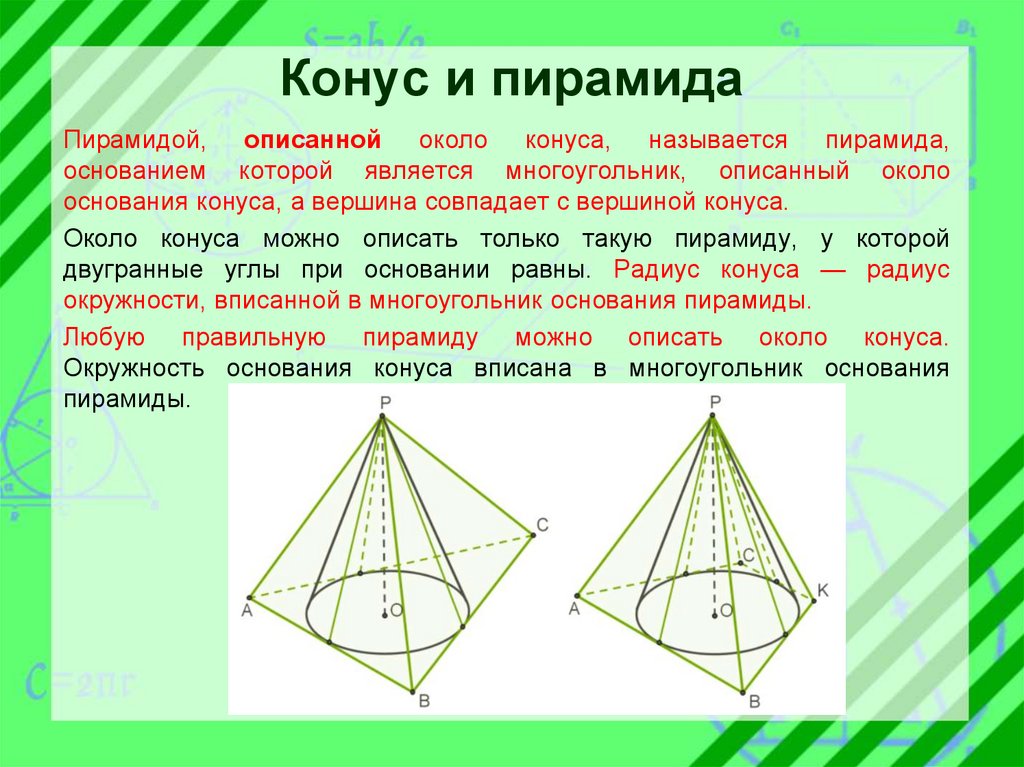
Конус и пирамидаПирамидой, описанной около конуса, называется пирамида,
основанием которой является многоугольник, описанный около
основания конуса, а вершина совпадает с вершиной конуса.
Около конуса можно описать только такую пирамиду, у которой
двугранные углы при основании равны. Радиус конуса — радиус
окружности, вписанной в многоугольник основания пирамиды.
Любую правильную пирамиду можно описать около конуса.
Окружность основания конуса вписана в многоугольник основания
пирамиды.
13.
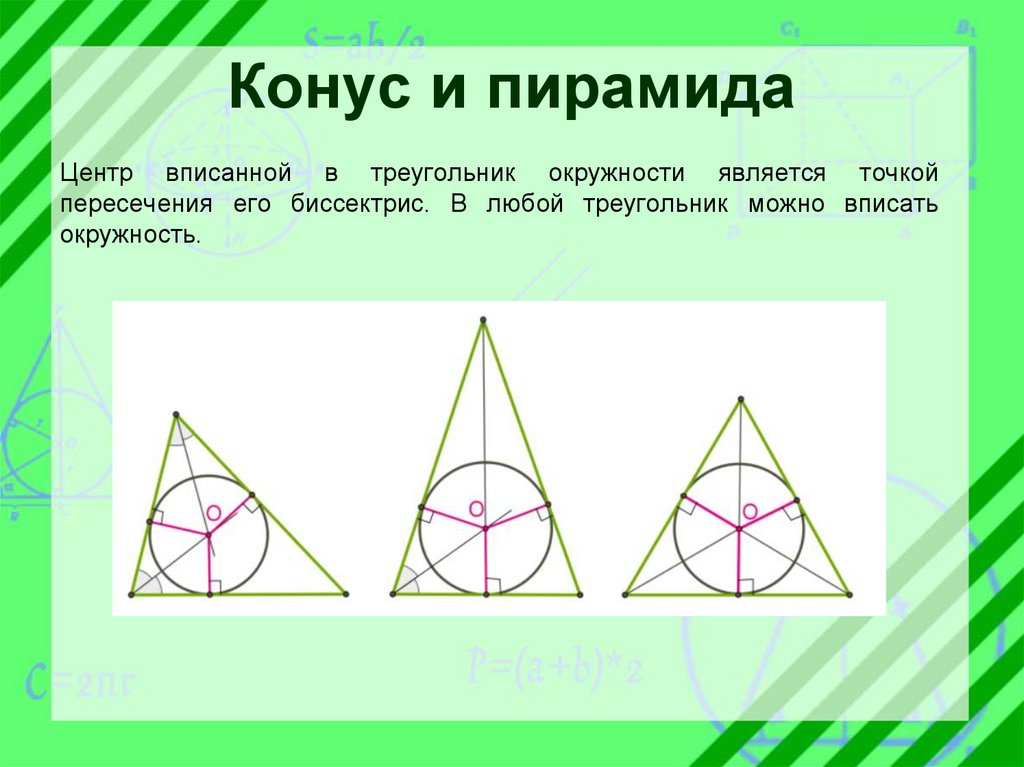
Конус и пирамидаЦентр вписанной в треугольник окружности является точкой
пересечения его биссектрис. В любой треугольник можно вписать
окружность.
14.
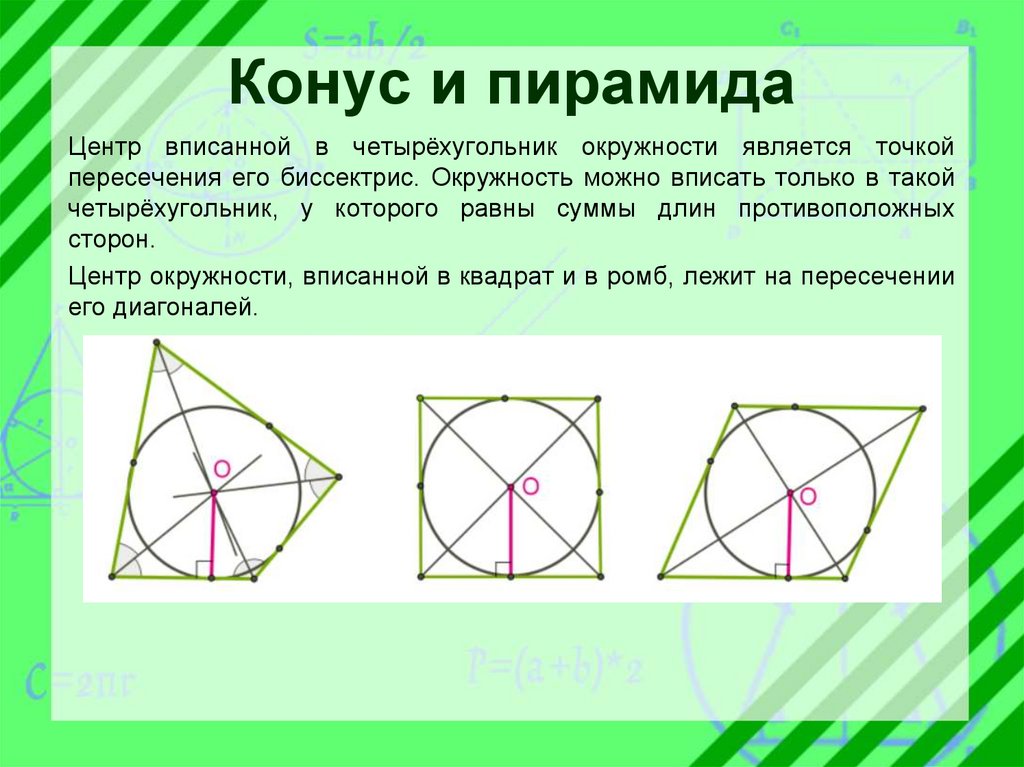
Конус и пирамидаЦентр вписанной в четырёхугольник окружности является точкой
пересечения его биссектрис. Окружность можно вписать только в такой
четырёхугольник, у которого равны суммы длин противоположных
сторон.
Центр окружности, вписанной в квадрат и в ромб, лежит на пересечении
его диагоналей.
15.
Конус и пирамидаПирамидой, вписанной в конус, называется такая пирамида,
многоугольник основания которой вписан в окружность основания конуса,
а вершиной является вершина конуса. В конус можно вписать только
такую пирамиду, боковые рёбра которой равны (совпадают
с образующими конуса).
Боковые рёбра равны у любой правильной пирамиды и у таких пирамид,
высота
которых
проецируется
в
центр
описанной
окружности.
Окружность
основания
конуса
описана
около
многоугольника основания пирамиды. Радиус конуса — радиус
окружности, описанной около многоугольника основания пирамиды.
16.
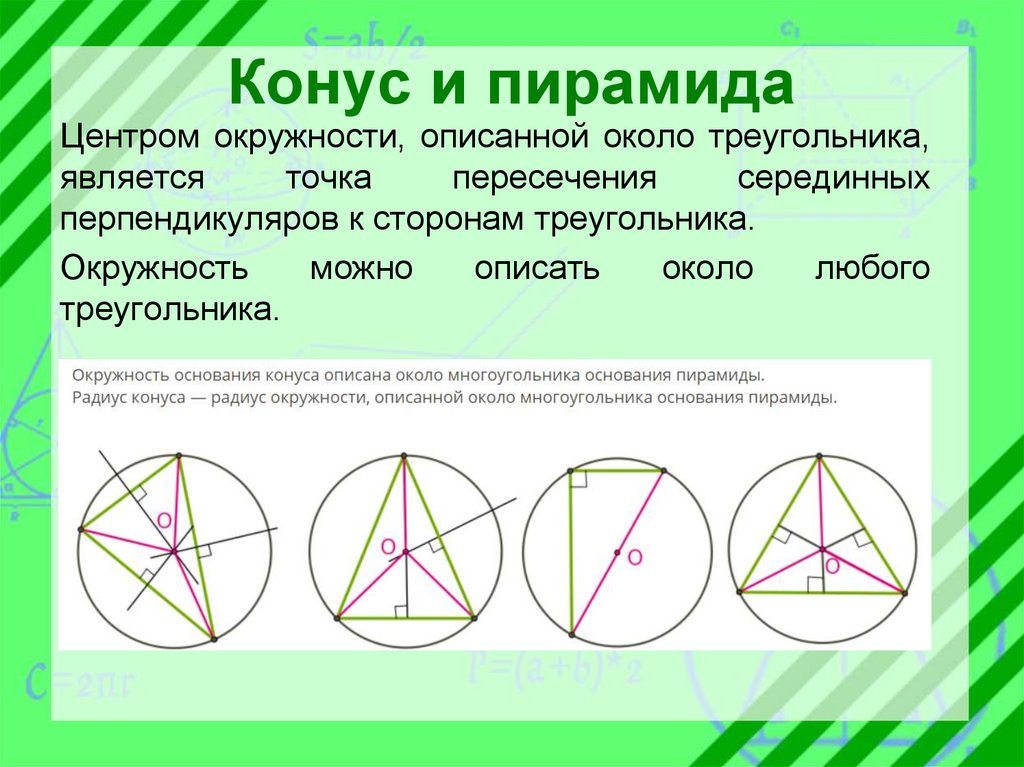
Конус и пирамидаЦентром окружности, описанной около треугольника,
является
точка
пересечения
серединных
перпендикуляров к сторонам треугольника.
Окружность
можно
описать
около
любого
треугольника.
17.
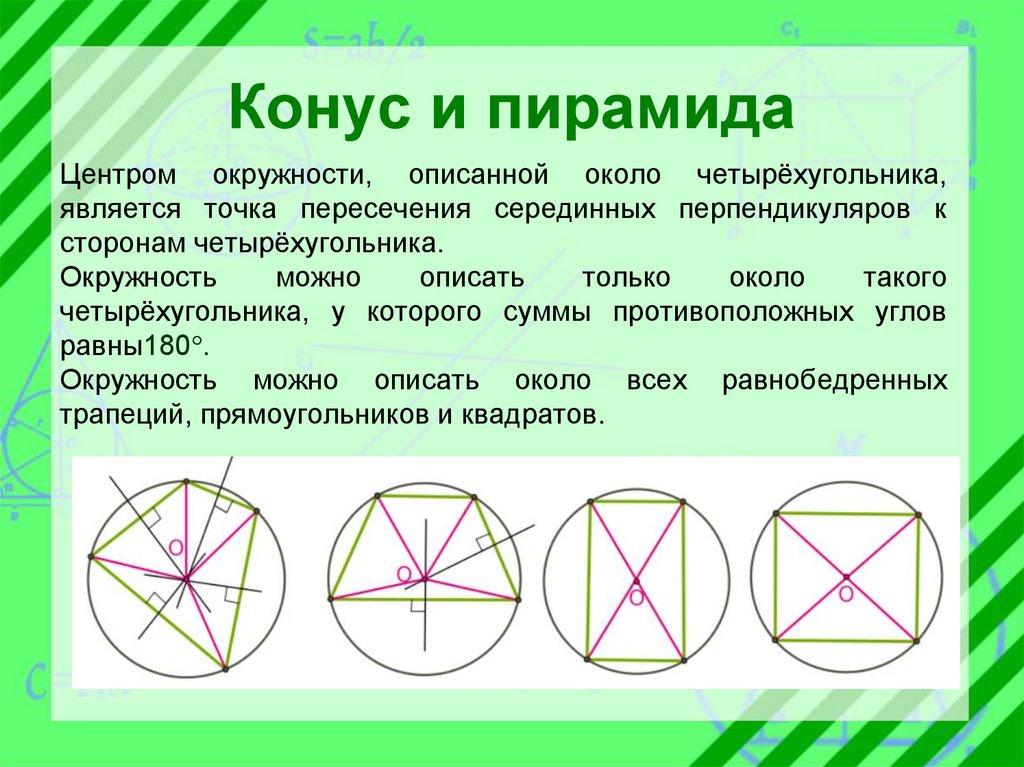
Конус и пирамидаЦентром окружности, описанной около четырёхугольника,
является точка пересечения серединных перпендикуляров к
сторонам четырёхугольника.
Окружность
можно
описать
только
около
такого
четырёхугольника, у которого суммы противоположных углов
равны180 .
Окружность можно описать около всех равнобедренных
трапеций, прямоугольников и квадратов.
18.
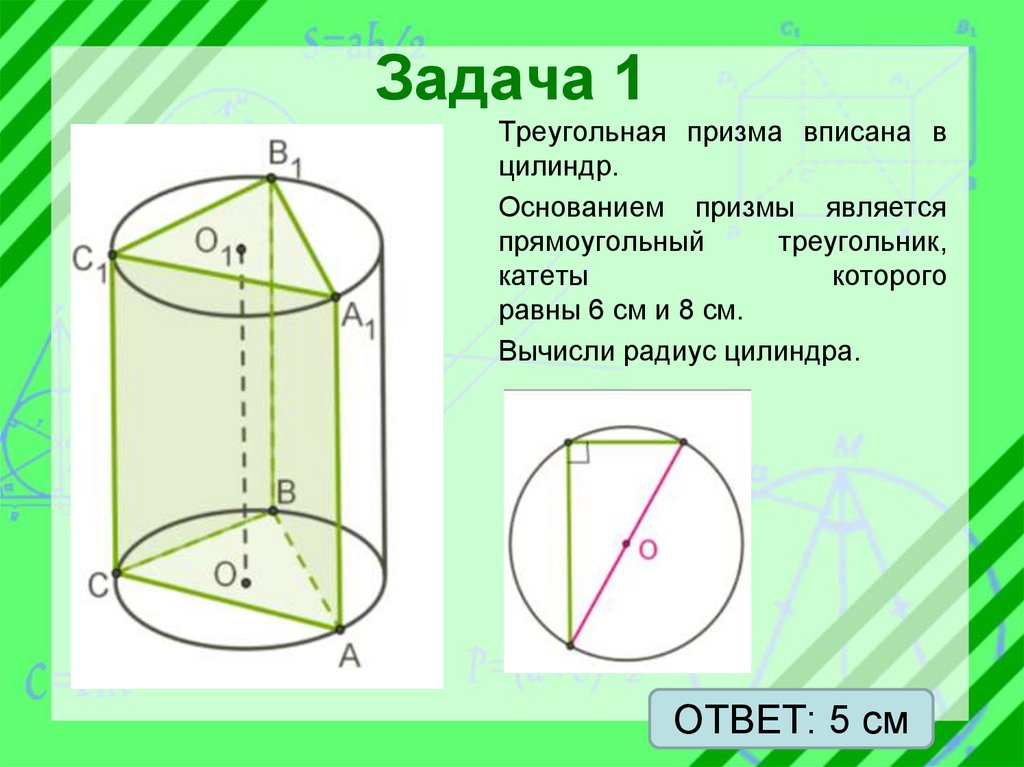
Задача 1Треугольная призма вписана в
цилиндр.
Основанием призмы является
прямоугольный
треугольник,
катеты
которого
равны 6 см и 8 см.
Вычисли радиус цилиндра.
ОТВЕТ: 5 см
19.
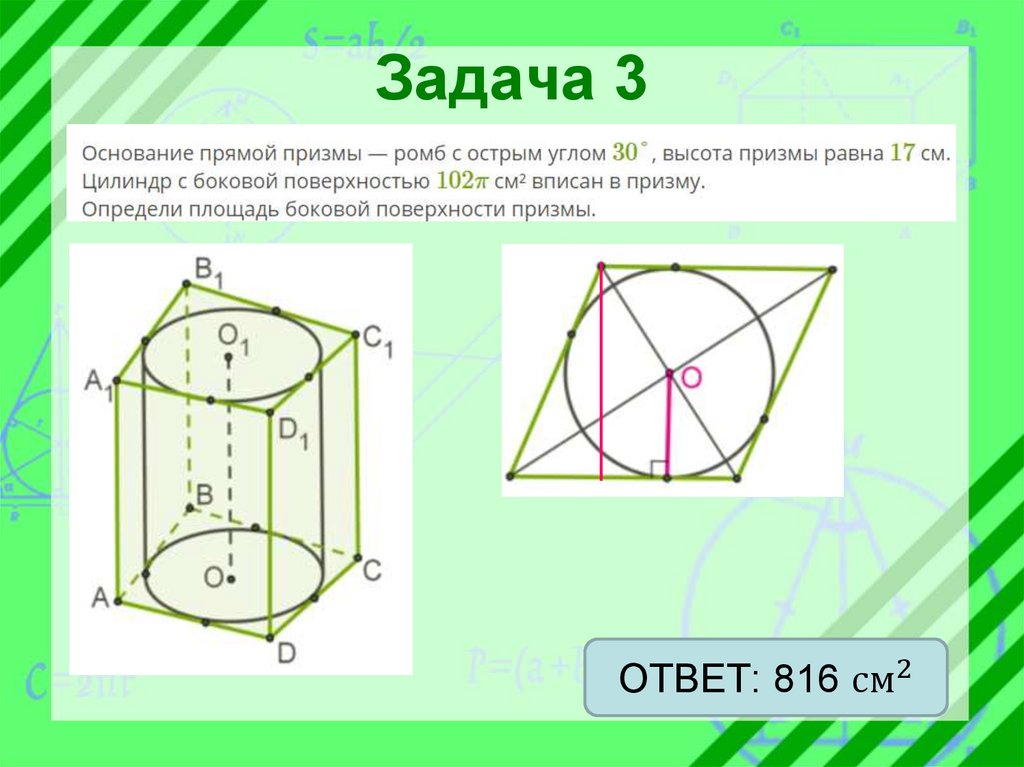
Задача 3ОТВЕТ: 816 см2
20.
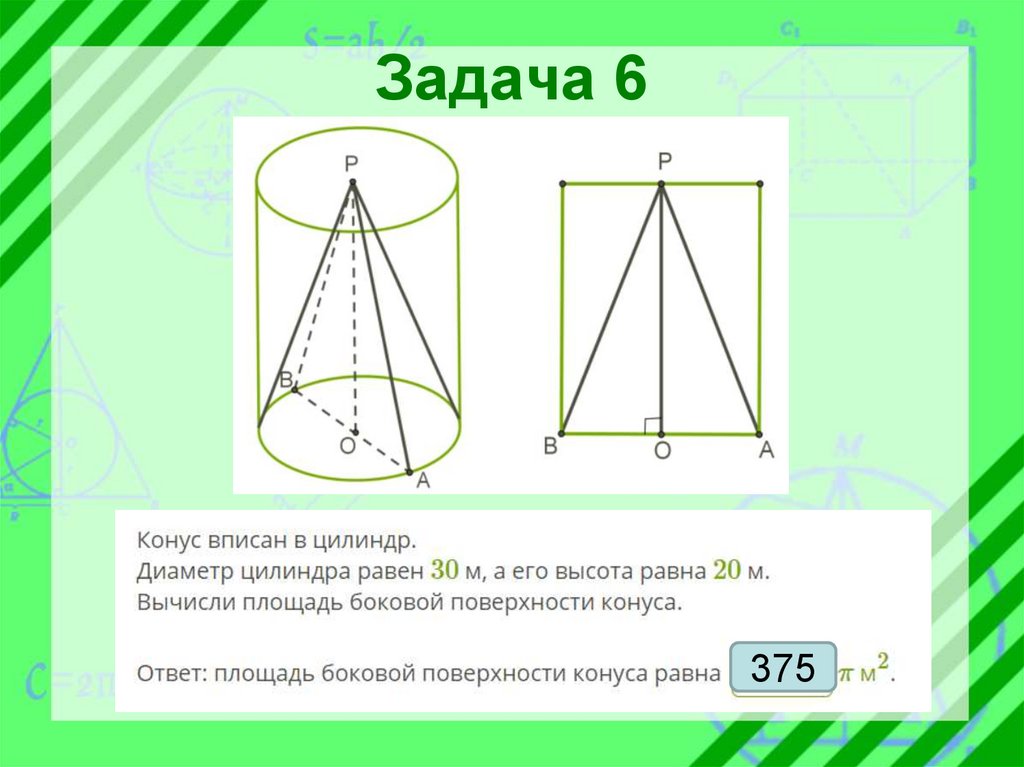
Задача 6375
21.
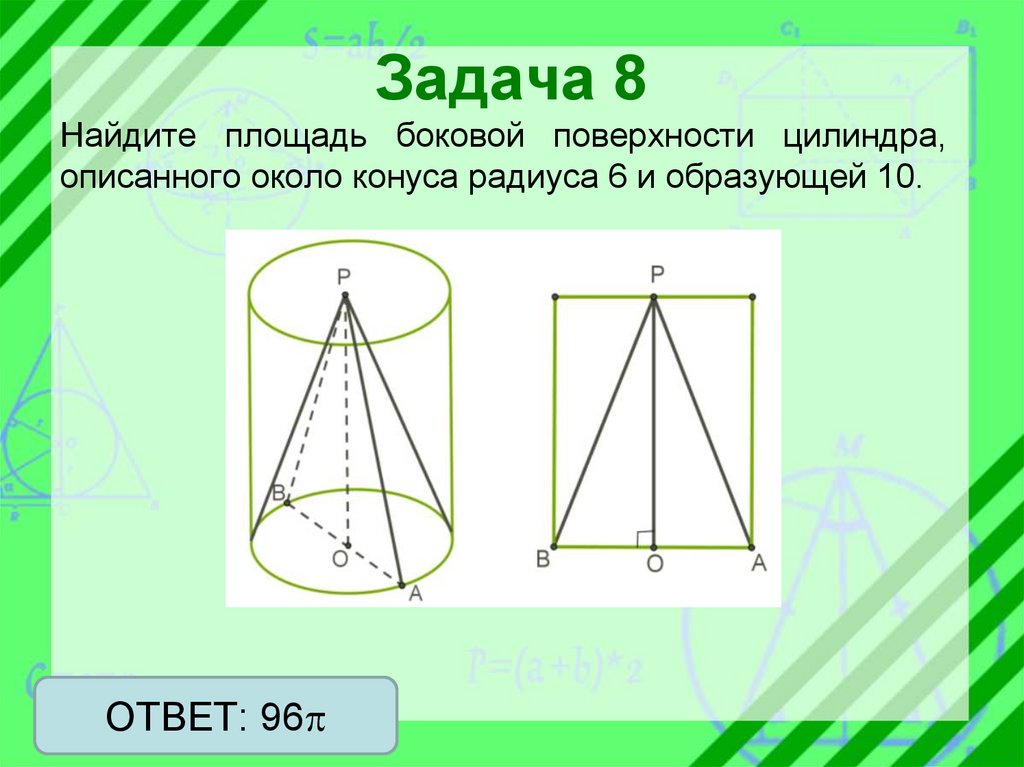
Задача 8Найдите площадь боковой поверхности цилиндра,
описанного около конуса радиуса 6 и образующей 10.
ОТВЕТ: 96
22.
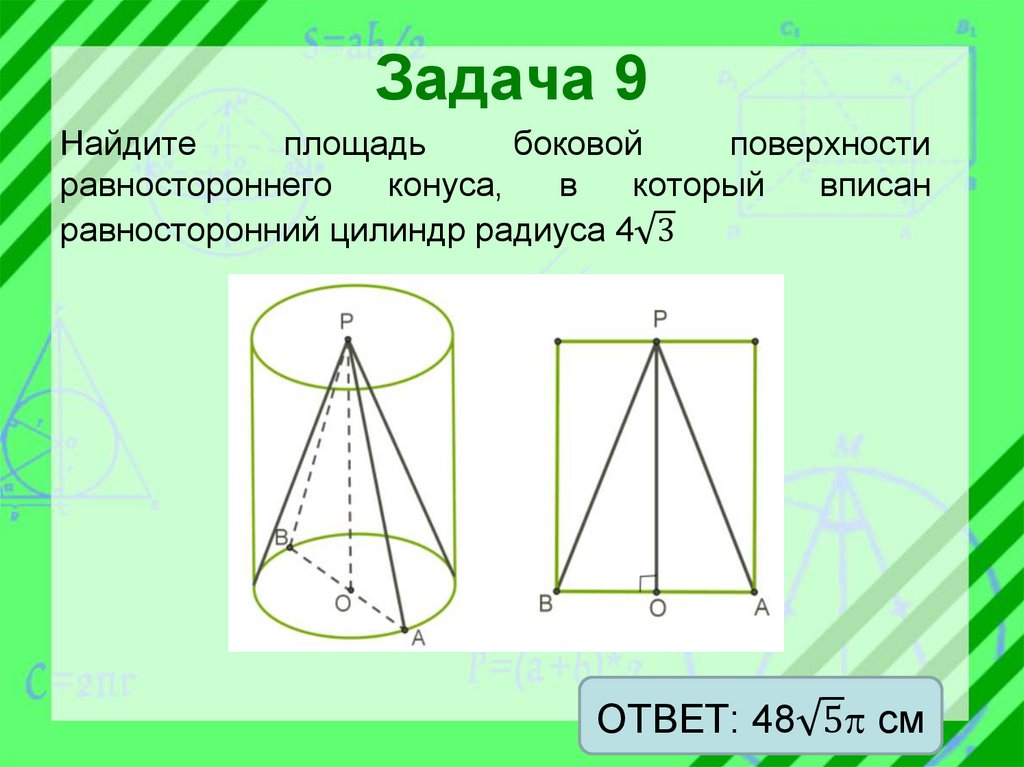
Задача 9Найдите
площадь
боковой
поверхности
равностороннего
конуса,
в
который
вписан
равносторонний цилиндр радиуса 4 3
ОТВЕТ: 48 5 см
23.
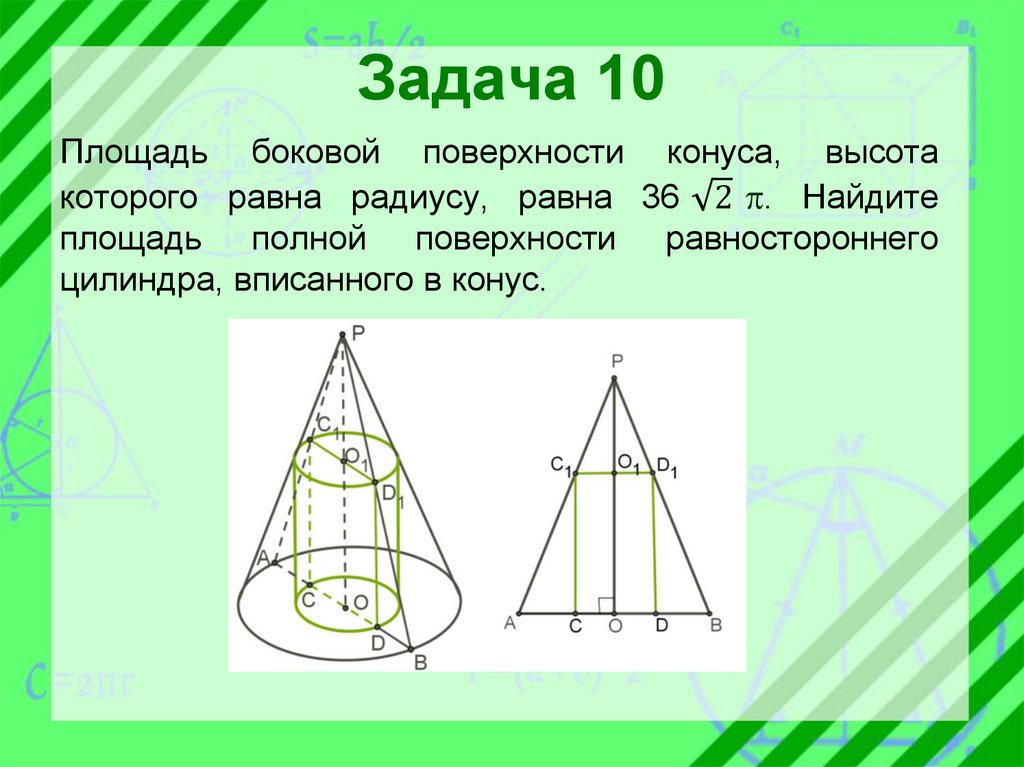
Задача 10Площадь боковой поверхности конуса, высота
которого равна радиусу, равна 36 2 . Найдите
площадь полной поверхности равностороннего
цилиндра, вписанного в конус.








 mathematics
mathematics








