ЕГЭ. Полный краткий справочник

1.

Справочные сведения
Полный краткий справочник
o Формулы сокращенного умножения
o Модуль числа, модуль выражения
o Степень с действительным показателем
o Корень n-ой степени из числа
o Логарифмы
o Арифметическая прогрессия
o Геометрическая прогрессия
o Бесконечно убывающая геометрическая прогрессия
o Основные формулы тригонометрии
o Производная и интеграл
o Треугольник
o Четырехугольники
o Окружность и круг
o Призма
o Пирамида
o Усеченная пирамида
o Цилиндр
o Конус
o Усеченный конус
o Сфера и шар
o Векторы и координаты
Особенности экзаменационных заданий профильной математики
o Задания 1: округление величин, проценты
▪ Особенности экзаменационных заданий на округление
▪ Округление величин с избытком и недостатком
▪ Проценты
▪ Особенности экзаменационных заданий на проценты
o Задания 2: анализ графических зависимостей
▪ Анализ графических зависимостей
▪ Особенности экзаменационных заданий на чтение графиков и диаграмм
o Задания 3 и 6: планиметрия
▪ Треугольник
▪ Равносторонний треугольник
▪ Равнобедренный треугольник
▪ Прямоугольный треугольник
▪ Тригонометрические функции дополнительных углов
▪ Основное тригонометрическое тождество и следствия из него
▪ Смежные углы
▪ Средняя линия треугольника
▪ Медиана треугольника
▪ Биссектриса треугольника
▪ Высота треугольника
▪ Серединный перпендикуляр
▪ Теорема косинусов
▪ Параллелограмм
▪ Прямоугольник
▪ Ромб
▪ Параллелограмм Вариньона
▪ Трапеция
▪ Правильный шестиугольник

2.

▪
▪
o
o
o
o
Теоремы о площадях многоугольников
Окружность
▪ Вписанный угол
▪ Хорда
▪ Касательная к окружности
▪ Секущая
▪ Круг и его элементы
▪ Соотношения между элементами окружности и круга
▪ Вписанная окружность
▪ Описанная окружность
▪ Вектор
▪ Сумма и разность векторов
▪ Координаты вектора
▪ Скалярное произведение векторов
▪ Расстояния от точки до координатных осей
▪ Расстояние между точками
Задания 4: вероятности событий
▪ Определение вероятности
▪ Теоремы о вероятностях событий
▪ Особенности экзаменационных заданий на начала теории вероятности
Задания 5: простейшие уравнения
▪ Простейшие уравнения
▪ Линейные уравнения
▪ Квадратные уравнения
▪ Рациональные уравнения
▪ Иррациональные уравнения
▪ Показательные уравнения
▪ Логарифмические уравнения
▪ Особенности решения экзаменационных заданий на простейшие уравнения
Задания 7: производные, первообразные
▪ Правила дифференцирования
▪ Производная числа, линейной и степенной функции
▪ Производная многочлена
▪ Уравнение прямой
▪ Уравнение касательной
▪ Физический смысл производной
▪ Монотонность и экстремумы функции
▪ Первообразная
▪ Криволинейная трапеция и ее площадь
Задания 8: стереометрия
▪ Особенности экзаменационных заданий по стереометрии
▪ Куб
▪ Призма. Прямоугольный параллелепипед
▪ Прямая призма
▪ Прямоугольный параллелепипед и его свойства
▪ Особенности правильной шестиугольной призмы
▪ Пирамида
▪ Сечения
▪ Цилиндр и его соотношения
▪ Конус и его соотношения
▪ Сфера и шар
▪ Комбинации круглых тел. Вписанные сферы
▪ Комбинации круглых тел. Описанные сферы
▪ Комбинации конуса и цилиндра

3.

▪
▪
▪
o
o
o
o
Комбинации многогранников и круглых тел. Описанные сферы
Комбинации многогранников и круглых тел. Вписанные сферы
Комбинации конуса, цилиндра и многогранников
Задания 9: тождественные преобразования выражений
▪ Действия с дробями
▪ Формулы сокращенного умножения
▪ Степень и её свойства
▪ Свойства степени
▪ Степень с дробным показателем
▪ Арифметический корень
▪ Свойства арифметического корня
▪ Определение логарифма и его свойства
▪ Основные тригонометрические формулы
▪ Правило для запоминания формул приведения
▪ Свойства четности и нечетности функций
Задания 10: задачи с прикладным содержанием
▪ Задачи с прикладным содержанием
Задания 11: текстовые задачи
▪ Определение процента
▪ Правило креста для решения задач на смеси
▪ Движение по прямой
▪ Движение по окружности
▪ Алгоритм решения задач на совместную работу
Задания 12: исследование функций при помощи производной
▪ Производная некоторых элементарных функций
▪ Правила дифференцирования
▪ Монотонность и экстремумы функции
▪ Наибольшее и наименьшее значение функции
Формулы сокращенного умножения
Модуль числа, модуль выражения
Определение
Основные свойства модуля
1.
2.

4.

3.
4.
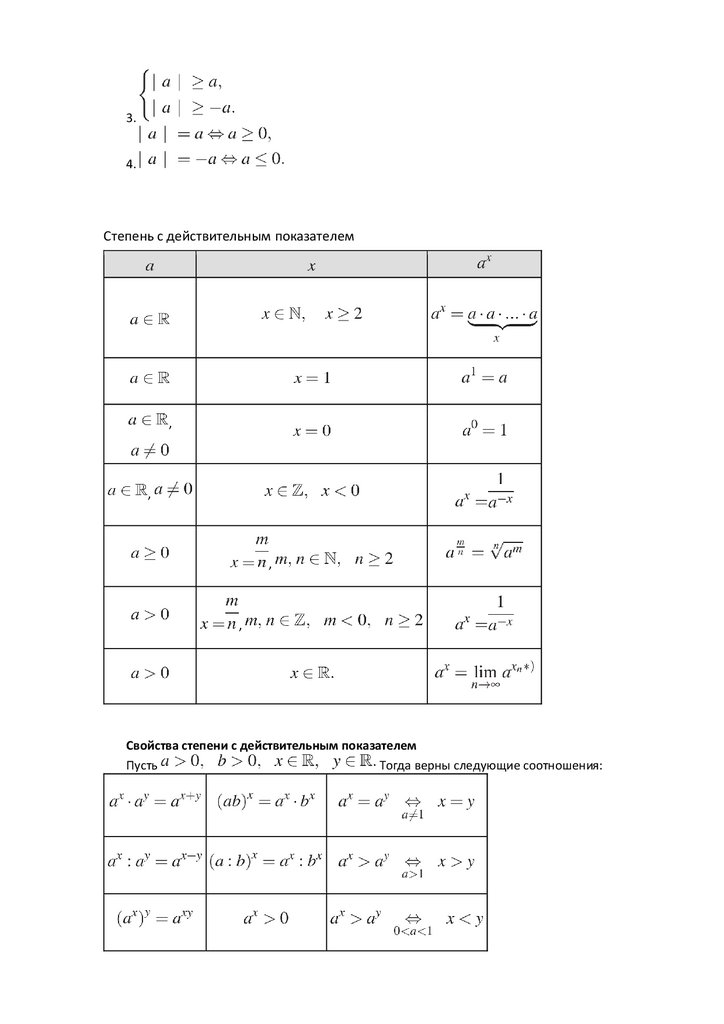
Степень с действительным показателем
,
,
,
,
Свойства степени с действительным показателем
Пусть
Тогда верны следующие соотношения:

5.

Корень n-ой степени из числа
Корнем n-ой степени
равна a.
из числа a называется число, n-ая степень которого
Арифметическим корнем четной степени n
из неотрицательного
числа a называется неотрицательное число, n-ая степень которого равна a.
Основные свойства арифметического корня
Логарифмы
Определение логарифма
Основное логарифмическое тождество
Основные свойства логарифмов
Пусть
шения:
Тогда верны следующие соотно-

6.

Арифметическая прогрессия
Формула n-го члена арифметической прогрессии
Характеристическое свойство арифметической прогрессии
Сумма n первых членов арифметической прогрессии
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными
также следующие формулы:
Геометрическая прогрессия
Формула n-го члена геометрической прогрессии
Характеристическое свойство геометрической прогрессии
Сумма n первых членов геометрической прогрессии

7.

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными
также следующие формулы
Бесконечно убывающая геометрическая прогрессия
Сумма бесконечно убывающей геометрической прогрессии
Основные формулы тригонометрии
Зависимость между тригонометрическими функциями одного аргумента
Формулы сложения

8.

Формулы тригонометрических функций двойного аргумента
Формулы понижения степени
Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения. Например:
Применение формул приведения укладывается в следующую схему:
— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что
;
— определяется знак приводимой функции;
— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид
или
, то функция меняется на сходственную
функцию, если аргумент приводимой функции имеет вид
Например, получим формулу
—
— IV четверть;
— в IV четверти тангенс отрицательный;
:
, то функция названия не меняет.

9.

— аргумент приводимой функции имеет вид
, следовательно, название функции ме-
няется. Таким образом:
Формулы преобразования суммы тригонометрических функций в произведение
Формулы преобразования произведения тригонометрических функций в сумму
Производная и интеграл
Таблица производных некоторых элементарных функций
Функция
c
Производная Функция
0
Производная

10.

Правила дифференцирования
1.
2.
3.
4.
5.
Уравнение касательной к графику функции
в его точке
:
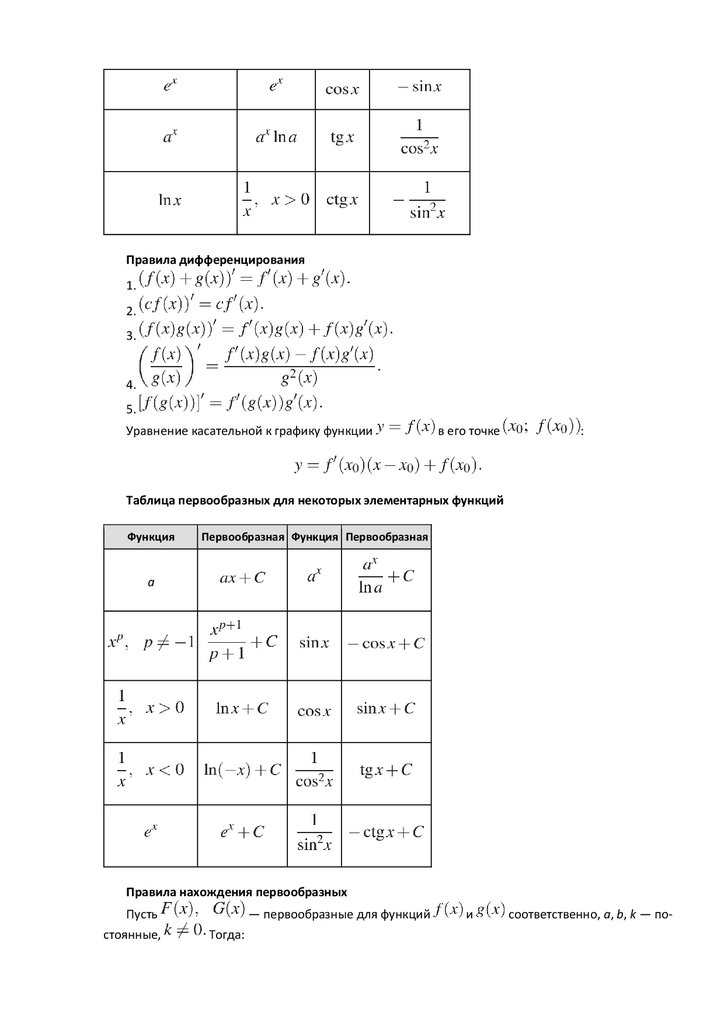
Таблица первообразных для некоторых элементарных функций
Функция
Первообразная Функция Первообразная
a
Правила нахождения первообразных
Пусть
стоянные,
― первообразные для функций
Тогда:
и
соответственно, a, b, k ― по-

11.

—
—
― первообразная для функции
― первообразная для функции
—
― первообразная для функции
— Формула Ньютона-Лейбница:
Четырехугольники
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определения следует,
что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и
ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не
параллельны.
Площадь четырехугольника
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между
ними.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на синус угла между
ними.
Треугольник
Пусть
но;
―
длины
сторон BC, AC, AB треугольника ABC соответствен-
―
полупериметр
треугольника ABC; A, B, C ―
величины
углов BAC, ABC, ACB треугольника ABC соответственно;
―
длины
высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около
треугольника ABC; r — радиус окружности, вписанной в треугольник ABC;
― площадь треугольника ABC. Тогда имеют место следующие соотношения:
(теорема синусов);
(теорема косинусов);

12.

Окружность и круг
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь
круга,
— длина дуги в градусов, — длина дуги в радиан,
— площадь сектора, ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в радиан. Тогда имеют
место следующие соотношения:
Вписанный угол
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Вписанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого
многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в
многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке. В четырехугольник можно вписать окружность
тогда и только тогда, когда суммы его противоположных сторон равны.
Описанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин
этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только
одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника
пересекаются в одной точке.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Призма
Пусть H ― высота призмы, AA1 ― боковое ребро призмы,
― периметр основания призмы,
― площадь основания призмы,
― площадь боковой поверхности призмы,
― площадь полной поверхности призмы, V ― объем призмы,
― периметр перпендикулярного сечения призмы,
― площадь перпендикулярного сечения призмы. Тогда имеют
место следующие соотношения:

13.

Свойства параллелепипеда
— Противоположные грани параллелепипеда равны и параллельны.
— Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
— Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Пирамида
Пусть H ― высота пирамиды,
― периметр основания пирамиды,
― площадь основания пирамиды,
― площадь боковой поверхности пирамиды,
― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:
;
.
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Усеченная пирамида
Пусть H ― высота усеченной пирамиды, и
― периметры оснований усеченной пирамиды, и
― площади оснований усеченной пирамиды,
― площадь боковой поверхности
усеченной пирамиды,
― площадь полной поверхности усеченной пирамиды, V ― объем
усеченной пирамиды.
Тогда имеют место следующие соотношения:
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Цилиндр
Пусть h ― высота цилиндра, r ― радиус цилиндра,
― площадь боковой поверхности цилиндра,
― площадь полной поверхности цилиндра, V ― объем цилиндра.
Тогда имеют место следующие соотношения:

14.

Конус
Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса,
― площадь боковой поверхности конуса,
― площадь полной поверхности конуса, V ― объем конуса.
Тогда имеют место следующие соотношения:
Усеченный конус
Пусть h ― высота усеченного конуса, r и ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,
― площадь боковой поверхности усеченного конуса, V ― объем
усеченного конуса. Тогда имеют место следующие соотношения:
Векторы и координаты
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется направленным отрезком или вектором.
Сумма и разность векторов
Для того, чтобы сложить неколлинеарные векторы
от какой-нибудь точки A векторы
Чтобы найти сумму
тора
векторов
и
и
векторов
достаточно отложить
и построить параллелограмм ABCD. Тогда
необходимо в конец вектора
и провести вектор из начала вектора
Чтобы найти разность
и
поместить начало век-
в конец вектора
и
вектора и провести вектор из конца вектора
Координаты вектора
необходимо в начало вектора
в конец вектора
поместить начало

15.

Пусть точка A имеет координаты
точка B имеет координаты
а точка С — середина отрезка АВ. Тогда координаты точки С равны полусумме соответствующих координат концов отрезка:
Пусть точка A имеет координаты
наты вектора
точка B имеет координаты
Тогда коорди-
равны разности соответствующих координат конца вектора и его начала:
Декартовы координаты вектора являются проекциями этого вектора на соответственные оси
систем координат.
Модуль вектора (длина вектора)
вычисляется по формуле
Пусть даны векторы
и
Тогда:
то есть действиям с векторами отвечают идентичные действия с их координатами.
Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов называется число, равное произведению
длин этих векторов на косинус угла между ними. Иными словами, скалярное произведение векторов — это число. Если через
ное произведение, то
обозначить угол между векторами
и
а через
— их скаляр-
Скалярное произведение выражается через координаты сомножителей по формуле:
Необходимым и достаточным условием перпендикулярности двух ненулевых векторов является равенство нулю их скалярного произведения:
Косинус угла
между векторами
и
определяется по формуле

16.

Поскольку косинус острого угла положителен, а косинус тупого угла — отрицателен, то, если
скалярное произведение положительно, векторы образуют острый угол, а если отрицательно —
тупой.
Расстояния от точки до координатных осей
Для определения расстояний от точки до осей координат применяют следующие утверждения.
— Модуль абсциссы точки равен расстоянию от этой точки до оси ординат.
— Модуль ординаты точки равен расстоянию от этой точки до оси абсцисс.
Расстояние между точками
Пусть точка A имеет координаты
стояние между ними находится по формуле:
точка B имеет координаты
тогда рас-
Особенности экзаменационных заданий на проценты
Экзаменационные задачи на вычисление процентов сводятся к одному из трех случаев.
– В задания типа «Найти а% от b» требуется найти произведение
– В заданиях типа «Сколько процентов составляет а от b?» находим
– В заданиях типа «Найдите число x, если а% от него равны b» находим
Задания 3 и 6: планиметрия
Проверяемые элементы содержания и виды деятельности: владение понятиями угол, отрезок, треугольник, медиана, биссектриса, высота, четырехугольник, многоугольник, центральный и
вписанный угол, окружность, тригонометрические функции угла, знание их свойств.
Ориентировочное время выполнения учащимися: 10—15 минут.
Типы заданий:
• Треугольник.
• Параллелограмм.
• Прямоугольник.
• Ромб.
• Квадрат.
• Трапеция.
• Центральные и вписанные углы.
• Хорда, касательная, секущая.
• Вписанная окружность.
• Описанная окружность.
• Нахождение тригонометрических функций внутренних углов.
• Нахождение тригонометрических функций внешних углов.
• Использование тригонометрических функций для нахождения длин.
• Правильные многоугольники.
• Комбинации правильных многоугольников и окружностей.

17.

Равносторонний треугольник
Треугольник, все три стороны которого равны, называется правильным (равносторонним) треугольником.
Пусть a, h, S, R, r — соответственно длина стороны, высота, площадь, радиус описанной и радиус вписанной окружности правильного треугольника. Тогда имеют место следующие соотношения:
Прямоугольный треугольник
Если один из углов треугольника прямой, то треугольник называется прямоугольным. В прямоугольном треугольнике сторона, лежащая против прямого угла называется гипотенузой, а две другие стороны называются катетами этого треугольника.
Обозначим через c гипотенузу AB прямоугольного треугольника ABC, через ac и bc — проекции
катетов a и b на гипотенузу AB, а через hc — высоту, проведенную из вершины прямого угла C этого
треугольника. Тогда имеют место следующие соотношения:

18.

Тригонометрические функции дополнительных углов
Тригонометрические функции дополнительных углов являются сходственными:
Основное тригонометрическое тождество и следствия из него
Основное тригонометрическое тождество и следствия из него:
Смежные углы
Синусы смежных углов равны, а косинусы, тангенсы и котангенсы противоположны:
Средняя линия треугольника
Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника. Средняя линия треугольника параллельна одной из сторон
треугольника и равна ее половине. Три средние линии треугольника делят его на 4 равных треугольника.

19.

Медиана треугольника
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Медианы треугольника пересекаются в
одной точке, и точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины.
Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности). Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам
треугольника.
Серединный перпендикуляр
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке (центре
описанной окружности).
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других его сторон, уменьшенной на
удвоенное произведение этих сторон на косинус угла между ними (теорема косинусов):
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны. Справедливы следующие утверждения.
– Две противоположные стороны четырехугольника равны и параллельны тогда и только тогда,
когда этот четырехугольник — параллелограмм.
– Противоположные стороны четырехугольника попарно равны тогда и только тогда, когда этот
четырехугольник — параллелограмм.
– Противоположные углы четырехугольника попарно равны тогда и только тогда, когда этот четырехугольник — параллелограмм.
– Диагонали четырехугольника пересекаются и точкой пересечения делятся пополам тогда и
только тогда, когда этот четырехугольник — параллелограмм.
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые. Так как прямоугольник, по определению, является параллелограммом, то он обладает всеми свойствами параллелограмма. Кроме того, прямоугольник обладает следующим характеристическим свойством.
Диагонали параллелограмма равны тогда и только тогда, когда этот параллелограмм — прямоугольник.

20.

Ромб
Ромбом называется параллелограмм, все стороны которого равны. Так как ромб, по определению, является параллелограммом, то он обладает всеми свойствами параллелограмма. Кроме того,
ромб обладает следующими характеристическими свойствами.
Диагонали параллелограмма делят его углы пополам тогда и только тогда, когда этот параллелограмм — ромб.
Диагонали параллелограмма взаимно перпендикулярны тогда и только тогда, когда этот параллелограмм — ромб.
Параллелограмм Вариньона
Середины сторон произвольного (в том числе невыпуклого или даже пространственного) четырехугольника являются вершинами параллелограмма
— параллелограмма Вариньона.
Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника.
Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.
Если исходный параллелограмм — прямоугольник, то параллелограмм Вариньона — ромб.
Если исходный параллелограмм — ромб, то параллелограмм Вариньона — прямоугольник. Если
исходный параллелограмм — квадрат, то параллелограмм Вариньона — квадрат.
Трапеция
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не
параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны
— боковыми сторонами. Отрезок, соединяющий середины боковых сторон трапеции называется
средней линией трапеции. Трапеция, боковые стороны которой равны, называется равнобедренной трапецией. Трапеция, один из углов которой прямой, равен называется прямоугольной трапецией. Трапеция обладает следующими свойствами.
– Средняя линия трапеции параллельна ее основаниям и равна их полусумме.
– Отрезок, соединяющие середины диагоналей трапеции, равен полуразности большего и
меньшего оснований.
– Диагонали трапеции равны тогда и только тогда, когда эта трапеция равно-бедренная.
– Углы при каждом основании трапеции равны тогда и только тогда, когда эта трапеция равнобедренная.
– Сумма противолежащих углов в равнобедренной трапеции равна 180°.
– В равнобедренной трапеции расстояние от вершины одного основания до проекции противоположной вершины на прямую, содержащую это основание, равно средней линии.

21.

Правильный шестиугольник
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него
окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в
раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями,
прямоугольный, а его острые углы равны 30° и 60°.
Теоремы о площадях многоугольников
Для вычисления площадей многоугольников применяют следующие теоремы.
– Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой
стороне или к ее продолжению.
– Площадь треугольника равна половине произведения сторон на синус угла между ними.
– Площадь квадрата равна квадрату его стороны.
– Площадь прямоугольника равна произведению его сторон.
– Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
– Площадь параллелограмма равна произведению сторон на синус угла между ними.
– Площадь ромба равна половине произведения его диагоналей.
– Площадь ромба равна произведению квадрата стороны на синус угла между сторонами.
– Площадь трапеции равна произведению полусуммы оснований на высоту.
– Площадь трапеции равна произведению средней линии на высоту.
– Площади подобных многоугольников относятся как квадрат коэффициента подобия.
–
Площадь
многоугольника,
вершины
которого
лежат
в
узлах
решетки,
равна
где В — количество узлов внутри многоугольника, а Г — количество узлов на
границе многоугольника.
Вписанный угол
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Справедливы следующие утверждения.
– Вписанный угол измеряется половиной дуги, на которую он опирается.

22.

– Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
– Вписанные углы, опирающиеся на одну и ту же дугу, равны.
– Вписанный угол, опирающийся на полуокружность, — прямой.
– Отношение хорды к синусу вписанного угла, который на нее опирается, равно двум радиусам
(теорема синусов).
Хорда
Отрезок, концы которого лежат на окружности, называется ее хордой. Справедливы следующие утверждения.
– Равные хорды стягивают равные дуги.
– Углы, опирающиеся на одну и ту же хорду, либо равны, либо в сумме дают 180°.
– Хорда, равная диаметру, из всех точек окружности видна под углом 90°.
– Радиус окружности, перпендикулярный хорде, делит ее пополам.
– Угол между двумя хордами равен полусумме высекаемых ими дуг:
– Произведение отрезков, на которые делится хорда данной точкой, есть для данной окружности величина постоянная и равная разности квадратов радиуса окружности и расстояния от точки
пересечения хорд до центра окружности:
Касательная к окружности
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности. Справедливы следующие утверждения.
– Отрезки касательных к окружности, проведенные из одной точки, равны.
– Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
– Угол между касательной и хордой, проходящей через точку касания, равен половине заключенной между ними дуги.
– Угол между двумя касательными к окружности, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг.

23.

Секущая
Прямая, имеющая с окружностью две общие точки, называется
секущей. Справедливы следующие утверждения.
– Угол между касательной и секущей, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:
– Квадрат касательной равен произведению секущей на ее внешнюю часть:
– Угол между секущими, проведенными из одной точки, равен
полуразности большей и меньшей высекаемых ими дуг:
– Произведение секущей на ее внешнюю часть есть для данной окружности величина постоянная и равная разности квадратов расстояния от точки пересечения секущих до центра окружности
и квадрата радиуса окружности:
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга,
— длина дуги в n градусов, — длина дуги в радиан,
— площадь сектора,
ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в радиан. Тогда
имеют место следующие соотношения:

24.

Вписанная окружность
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Многоугольник в этом случае называется описанным около окружности.
Центр окружности, вписанной в многоугольник, есть точка, равноудаленная от всех сторон
этого многоугольника, — точка пересечения биссектрис углов этого многоугольника. В многоугольник можно вписать окружность и притом только одну, тогда и только тогда, когда биссектрисы его
углов пересекаются в одной точке.
В любой треугольник можно вписать окружность.
В правильный многоугольник можно вписать окружность.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Если окружность радиуса r вписана в многоугольник, площадь которого равна S, а полупериметр равен p, то имеет место соотношение
площадь описанного многоугольника равна
произведению полупериметра на радиус вписанной окружности.
Если окружность вписана в правильный треугольник, то ее радиус r выра-
жается через его сторону a по формуле
Если окружность радиуса r вписана в прямоугольный треугольник с катетами а и b и гипотенузой с, то
Если окружность вписана в квадрат, то ее радиус равен половине стороны квадрата.
Описанная окружность
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника
принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.
Центр окружности, описанной вокруг многоугольника, есть точка, равноудаленная от всех вершин этого многоугольника, — точка пересечения серединных перпендикуляров к сторонам этого
многоугольника. Около многоугольника можно описать окружность и притом только одну, тогда и
только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в
одной точке.

25.

Около любого треугольника можно описать окружность. Радиус описанной окружности равен
отношению половины стороны к синусу противолежащего угла:
Около правильного многоугольника можно описать окружность.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Около трапеции можно описать окружность тогда и только тогда, когда эта трапеция равнобедренная.
Сумма и разность векторов
Для того, чтобы сложить неколлинеарные векторы
жить от какой-нибудь точки A векторы
и
и
достаточно отло-
и построить параллелограмм ABCD.
Тогда
Чтобы найти сумму
вектора
и
и провести вектор из начала вектора
Чтобы найти разность
вектора
векторов
векторов
и
и провести вектор из конца вектора
необходимо в конец вектора
поместить начало
в конец вектора
необходимо в начало вектора
поместить начало
в конец вектора
Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов называется число, равное произведению
длин этих векторов на косинус угла между ними. Иными словами, скалярное произведение векторов — это число. Если через
ное произведение, то
обозначить угол между векторами
и
а через
— их скаляр-
Скалярное произведение выражается через координаты сомножителей по формуле:

26.

Необходимым и достаточным условием перпендикулярности двух ненулевых векторов является равенство нулю их скалярного произведения:
Косинус угла
между векторами
и
определяется по формуле
Поскольку косинус острого угла положителен, а косинус тупого угла — отрицателен, то, если
скалярное произведение положительно, векторы образуют острый угол, а если отрицательно —
тупой.
Расстояния от точки до координатных осей
Для определения расстояний от точки до осей координат применяют следующие утверждения.
– Модуль абсциссы точки равен расстоянию от этой точки до оси ординат.
– Модуль ординаты точки равен расстоянию от этой точки до оси абсцисс.
Расстояние между точками
Пусть точка A имеет координаты
стояние между ними находится по формуле:
точка B имеет координаты
тогда рас-
Теоремы о вероятностях событий
Теорема. Вероятность произведения двух независимых событий A и B равна произведению
этих вероятностей:
Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих
событий:
Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих
событий минус вероятность их произведения:
Пусть А и В — зависимые события. Условной вероятностью PA(B) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое
событие уже наступило:

27.

Особенности экзаменационных заданий на начала теории вероятности
Большая часть заданий этого типа сводятся к использованию формулы
Напомним,
что ответом к задачам с кратким ответом могут быть только целые числа или конечные десятичные
дроби, поэтому полученную обыкновенную дробь необходимо переводить в десятичную.
Во избежание ошибок следует различать два типа условий. В условиях вида «из 100 сумок 8
дефектных» имеется в виду, что всего сумок 100, из них дефектных — 8, качественных — 92. В условиях вида «на каждые 100 сумок приходится 8 дефектных» предполагается, что всего сумок 108, из
них дефектных — 8, качественных — 100. Приведем пример такого задания.
Задание. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь
сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение. По условию из 108 сумок 100 являются качественными. Поэтому искомая вероятность
равна
Ответ: 0,93.
При решении заданий с использованием теорем о вероятностях событий важно хорошо знать
вышеприведённые определения и теоремы и не путаться в них. Вычислительной сложности задания, как правило, не представляют.
Показательные уравнения
Показательные уравнения, включенные в задания ЕГЭ, приводятся к одному из двух
типов:
типов.
или
Сформулируем теорему для решения уравнений указанных
Решение простейших показательных уравнений. Пусть
Тогда:
Логарифмические уравнения
Логарифмические уравнения, включенные в задания ЕГЭ, приводятся к одному из трех
типов:
формулы свойств логарифмов:
Для этого могут понадобиться
Сформулируем теорему для решения уравнений указанных типов.
Решение простейших логарифмических уравнений. Пусть
Тогда:

28.

Правила дифференцирования
Пусть функции f и g определены и дифференцируемы на некотором множестве I,
любые действительные числа. Тогда на множестве I справедливы соотношения:
и
—
Производная числа, линейной и степенной функции
Производная числа, линейной и степенной функции. Пусть k и n — любые числа, а x принимает
такие значения, что обе части каждой из формул имеют смысл. Тогда справедливы формулы:
В частности:
Производная многочлена
Производная многочлена равна сумме производных всех его членов.
Уравнение прямой
Если прямая не параллельна оси Oy, то ее уравнение может быть записано в
виде
Коэффициент k называют угловым коэффициентом прямой:
где —
величина
угла
между
этой
прямой
и
положительным
направлением
оси Ox,

29.

Уравнение касательной
Уравнение касательной к графику функции
лой
где
в его точке
задается форму-
— угловой коэффициент касательной.
Физический смысл производной
Пусть материальная точка движется по прямой так, что ее координата зависит от времени по
закону
Тогда скорость материальной точки меняется по закону
, а ее уско-
рение меняется по закону
Монотонность и экстремумы функции
Пусть дан график производной функции, определенной во всех точках некоторого промежутка.
Существование конечной производной означает дифференцируемость функции на этом промежутке, а значит, влечет существование и непрерывность самой функции на нем. Тогда для определения
поведения функции по знаку ее производной можно использовать следующие утверждения.
Если производная функции положительна на некотором промежутке, то функция возрастает на
нем.
Если производная функции отрицательна на некотором промежутке, то функция убывает на
нем.
Если производная функции в некоторой точке меняет знак с плюса на минус, то функция имеет
в этой точке максимум.
Если производная функции в некоторой точке меняет знак с минуса на плюс, то функция имеет
в этой точке минимум.
Первообразная
Функция
называется первообразной функции
на некотором промежутке, если для
всех x из этого промежутка
Приведем таблицу первообразных некоторых функций
(в ней k, n, C — постоянные, x — переменная):
Справедливы следующие утверждения.
– Если
— первообразная
а
— первообразная
то
— пер-
вообразная
– Если
есть первообразная для
а k — постоянная, то
есть первообразная
для
– Первообразная многочлена равна сумме первообразных всех его членов.
Криволинейная трапеция и ее площадь
Пусть на отрезке
задана непрерывная неотрицательная функция
Криволинейной
трапецией называется фигура, ограниченная графиком этой функции, осью абсцисс и прямыми
и

30.

Если при этом функция
является первообразной функции
щадь криволинейной трапеции вычисляется по формуле
на отрезке
то пло-
Эта разность перво-
образных обозначается также
Куб
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба,
— диагональ основания, — диагональ куба,
— площадь полной поверхности, а V — объем куба, то справедливы формулы:
Призма. Прямоугольный параллелепипед
Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.
Правильной призмой называется прямая призма, основание которой — правильный многоугольник.
Прямая призма
Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы —
прямоугольники.
Соотношения для прямой призмы
Пусть H — высота прямой призмы, AA1 — боковое ребро,
— периметр основания,
—
площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:

31.

Прямоугольный параллелепипед и его свойства
Прямая призма, у которой основанием является прямоугольник,
называется прямо-угольным параллелепипедом. Длины непараллельных ребер прямоугольного
параллелепипеда называются его линейными размерами (измерениями). Помимо свойств призмы,
прямоугольных параллелепипед обладает следующими свойствами.
– Противоположные грани прямоугольного параллелепипеда — параллельные и равные прямоугольники.
– Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам.
– Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений:
– Площадь полной поверхности прямоугольного параллелепипеда равна удвоенной сумме попарных произведений его измерений:
– Объем прямоугольного параллелепипеда равен произведению его измерений
Особенности правильной шестиугольной призмы
В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него
окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в
раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями,
прямоугольный, а его острые углы равны 30° и 60°.
Пирамида
Пусть вне плоскости многоугольника
задана точка P. Тогда фигура, образован-
ная треугольниками
,
и многоугольником
внутренними областями называется пирамидой (n-угольной пирамидой).
вместе с их

32.

Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.
Соотношения для правильной пирамиды
Пусть H — высота правильной пирамиды, h — ее апофема,
— периметр основания пирамиды,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место
следующие соотношения:
Сечения
Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой
имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

33.

Теоремы, используемые при построении сечений
Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.
Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и
пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости
то
она параллельна и самой плоскости
Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой
грани, то она пересекается со своей проекцией на эту грань.
Алгоритм построения сечений
Для построения сечений рекомендуем пользоваться следующим алгоритмом.
1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них
прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.
2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то
находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные
точки — новые точки секущей плоскости, лежащие в плоскостях граней.
3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.
Для контроля правильности построенного сечения, проверяйте, что:
– все вершины сечения лежат на рёбрах многогранника;
– все стороны сечения лежат в гранях многогранника;
– в каждой грани многогранника лежит не более одной стороны сечения.
Цилиндр и его соотношения
Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.
Соотношения для цилиндра

34.

Пусть h — высота цилиндра, r — радиус основания, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место
следующие соотношения:
Конус и его соотношения
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг
оси, содержащей его катет.
Соотношения для конуса
Пусть h — высота конуса, r — радиус основания, l — образующая, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем конуса. Тогда имеют
место следующие соотношения:
Сфера и шар
Шаром называется фигура, полученная при вращении полукруга вокруг оси,
содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:

35.

Комбинации круглых тел. Вписанные сферы
Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.
Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.
Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и
всех его образующих.
Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его
высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.
Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть
точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.
Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть
середина оси усечённого конуса.
Комбинации круглых тел. Описанные сферы
Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.
Сфера называется описанной около конуса, если вершина конуса и его основание лежат на
сфере.
Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.
Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём
центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.
Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр
сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной
какой-либо из его образующих и проходящей через ее середину.

36.

Комбинации конуса и цилиндра
Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса,
а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае
называется описанным вокруг цилиндра.
Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.
Комбинации многогранников и круглых тел. Описанные сферы
Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.
Возможность описать сферу около многогранника означает существование точки (центра
сферы), равноудалённой ото всех вершин многогранника.
Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на
какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.
Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на
какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного
около соответствующей грани.
Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около
соответствующей грани.
Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений
всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.
Комбинации многогранников и круглых тел. Вписанные сферы
Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.
Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r,
то справедливо соотношение:

37.

Комбинации конуса, цилиндра и многогранников
В условиях задач встречаются также следующие понятия, не входящие
в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее
употребительные из них.
Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.
Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.
Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.
Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.
Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.
Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.
Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между
собой.
Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.
Определение логарифма и его свойства
Логарифмом положительного числа b по основанию а
называют показатель
степени, в которую нужно возвести число а, чтобы получить число b. Для логарифма положительного числа b по основанию а
По определению
ством.
Частные случаи:
используется обозначение
это равенство называется основным логарифмическим тожде-
Логарифм положительного числа b по основанию 10 называется десятичным логарифмом и
обозначается
Логарифм положительного числа b по основанию е называется натуральным логарифмом и
обозначается

38.

Свойства логарифмов
Если
ствительное число, то справедливы следующие свойства:
— любое дей-
Основные тригонометрические формулы
Основные тригонометрические формулы:
Правило для запоминания формул приведения
Чтобы записать формулу приведения для аргументов
необходимо:
1) определить четверть, в которой лежит аргумент приводимой функции, предполагая
рым углом;
2) определить знак приводимой функции в этой четверти;
ост-

39.

3) определить вид функции, не изменяя ее для аргументов
для остальных аргументов.
и изменив на сходственную
А именно:
Свойства четности и нечетности функций
Свойства четности и нечетности функций
Задачи с прикладным содержанием
Любая из задач указанного типа может быть сведена либо к уравнению, либо к неравенству.
Выбор того или иного пути решения чаще всего будет обусловлен личными предпочтениями решающего. Из общих соображений можно сказать, что решать уравнение, как правило, проще, чем неравенство, но интерпретация полученного решения иногда может быть затруднительна. В учебных
целях мы предлагаем решать задачи двумя способами, вне зависимости от того, какой именно
более эффективен в данной конкретной задаче.
Задания с прикладным содержанием, представляют собой задачи на анализ явления, описываемого формулой функциональной зависимости. Каждая из фабул представляет собой описание
того или иного явления с указанием формулы, которой оно описывается, параметров и констант в
этой формуле и необходимых единиц измерения. В задачах с физическим содержанием все единицы измерения приведены в единой используемой в задаче системе единиц (СИ или СГС), перевод
единиц измерения из одной системы в другую не требуется.
Решение предложенных задач условно можно разделить на несколько шагов: а) анализ условия
и вычленение формулы, описывающей заданную ситуацию, а также значений параметров, констант
или начальных условий, которые необходимо подставить в эту формулу; б) математическая интерпретация вопроса задачи — сведение ее к уравнению или неравенству и его решение; в) анализ
полученного решения. Следует обратить особое внимание на интерпретацию результатов вычислений.

40.

Определение процента
Процент от числа — это сотая доля этого числа. Задача найти p% от а, эквивалентна задаче вычислить произведение
ем:
или
Например, вычисляя 6% от 150, получа-
Справедливы следующие утверждения.
– Если некоторое число а увеличить на p%, то получим
– Если некоторое число а уменьшить на p%, то получим
– Если некоторое число а увеличить на
оно получим
а полученный результат уменьшить на
– Положенная в банк под p% годовых начальная сумма
стигнет величины
то
через n лет с учетом процентов до-
Правило креста для решения задач на смеси
Если смешивать некоторое массу a-процентного раствора некоторого вещества с некоторой
массой b-процентного раствора этого же вещества,
то чтобы получить x-процентную смесь,
то исходные вещества надо брать в соотношении
к
(см. табл.):
a
x
b
Движение по прямой
Пусть скорости двух тел, начинающих движение одновременно, путь
ними S. Тогда:
и
расстояние между
– при движении навстречу друг другу они встретятся через время
– при движении в одну сторону и при
первое тело догонит второе через
время
– при движении в противоположные стороны тела через время t будут находиться друг от друга
на расстоянии
– Если тело движется по течению реки, то скорость тела относительно берега w равна сумме
скорости тела в стоячей воде v и скорости течения реки u:
– Если тело движется против течения реки, причем скорость тела в стоячей воде v больше скорости течения реки u, то скорость тела относительно берега
Если же скорость тела в
стоячей воде меньше скорости течения реки, то течение будет сносить тело со скоростью

41.

Для извлечения корня из дискриминантов полезна таблица квадратов:
Большинство экзаменационных задач на движение могут быть решены при помощи следующего алгоритма:
– обозначаем неизвестную величину буквой x, выясняем область ее определения;
– составляем таблицу со столбцами «Скорость», «Время», «Расстояние»;
– заполняем два столбца таблицы, вписывая в них x и данные задачи;
– заполняем оставшийся «ключевой» столбец по формулам
– составляем уравнение на данные ключевого столбца таблицы;
– решаем полученное уравнение на области определения x, и находим неизвестную.
Движение по окружности
Пусть скорости двух тел, начинающих движение одновременно, суть и
тогда:
– при движении в одном направлении по замкнутой траектории длины S при условии
тела, отправившиеся из одной точки, снова встретятся через время
– при встречном движении по замкнутой траектории длины S тела, отправившиеся из одной
точки, снова встретятся через время
Алгоритм решения задач на совместную работу
Большинство экзаменационных задач на совместную работу могут быть решены при помощи
следующего алгоритма:
– обозначаем неизвестную величину буквой x, выясняем область ее определения;
– составляем таблицу со столбцами «Производительность», «Время», «Объем работы»;
– заполняем два столбца таблицы, вписывая в них x и данные задачи; если объем работы не
задан принимаем его за 1;
–
заполняем
оставшийся
«ключевой»
столбец
по
формулам
или
или
связывающим объем работы V, производительность v и
время t.
– составляем уравнение на данные ключевого столбца таблицы;
– решаем полученное уравнение на области определения x, и находим неизвестную.
Производная некоторых элементарных функций
Пусть k и n — любые числа,
а x принимает такие значения, что обе части каждой
из формул имеют смысл. Тогда справедливы формулы:

42.

В частности:
Правила дифференцирования
Пусть функции f и g определены и дифференцируемы на некотором множестве I,
любые действительные числа. Тогда на множестве I справедливы соотношения:
и
—
В частности, производная многочлена равна сумме производных всех его членов.
Монотонность и экстремумы функции
Пусть дан график производной функции, определенной во всех точках некоторого промежутка.
Существование конечной производной означает дифференцируемость функции на этом промежутке, а значит, влечет существование и непрерывность самой функции на нем. Тогда для определения
поведения функции по знаку ее производной можно использовать следующие утверждения.
Если производная функции положительна на некотором промежутке, то функция возрастает на
нем.
Если производная функции отрицательна на некотором промежутке, то функция убывает на
нем.
Если производная функции в некоторой точке меняет знак с плюса на минус, то функция имеет
в этой точке максимум.
Если производная функции в некоторой точке меняет знак с минуса на плюс, то функция имеет
в этой точке минимум.
Наибольшее и наименьшее значение функции
Для определения наибольшего и наименьшего значений функции на отрезке используют следующие утверждения.
Пусть функция непрерывна на отрезке. Тогда наибольшее и наименьшее на этом отрезке значение функции достигается либо в критических точках, либо на концах отрезка.
Пусть функция непрерывна на отрезке
наибольшее и наименьшее на отрезке
мума, либо на концах отрезка.
и дифференцируема на интервале
Тогда
значение функции достигается либо в точках экстре-