Презентация 8 класс по Вероятности и статистике на тему _Множество подмножество_ (1)

1.

18.11.2024
Множество,
подмножество
8 класс Вероятность и статистика
Урок 8

2.

Повторение
Вопросы:
Всегда ли средние характеристики числового ряда
могут дать точную информацию о нём?
Что такое отклонение?
Что такое дисперсия?
Что такое стандартное отклонение (среднее
квадратичное)
В каком случае для сравнения числовых наборов
можно использовать суммы квадратов отклонений?
В каком случае для сравнения числовых наборов
предпочтительно вычислить их дисперсии?

3.

Множество, подмножество
Цели:
изучить, что такое множество и подмножество,
рассмотреть примеры., что являемся
дополнением множества,
учиться решать задачи на множества
Ключевые слова:
Множество
Способы задания множеств
Знак принадлежности множеству
Пустое множество
Подмножество
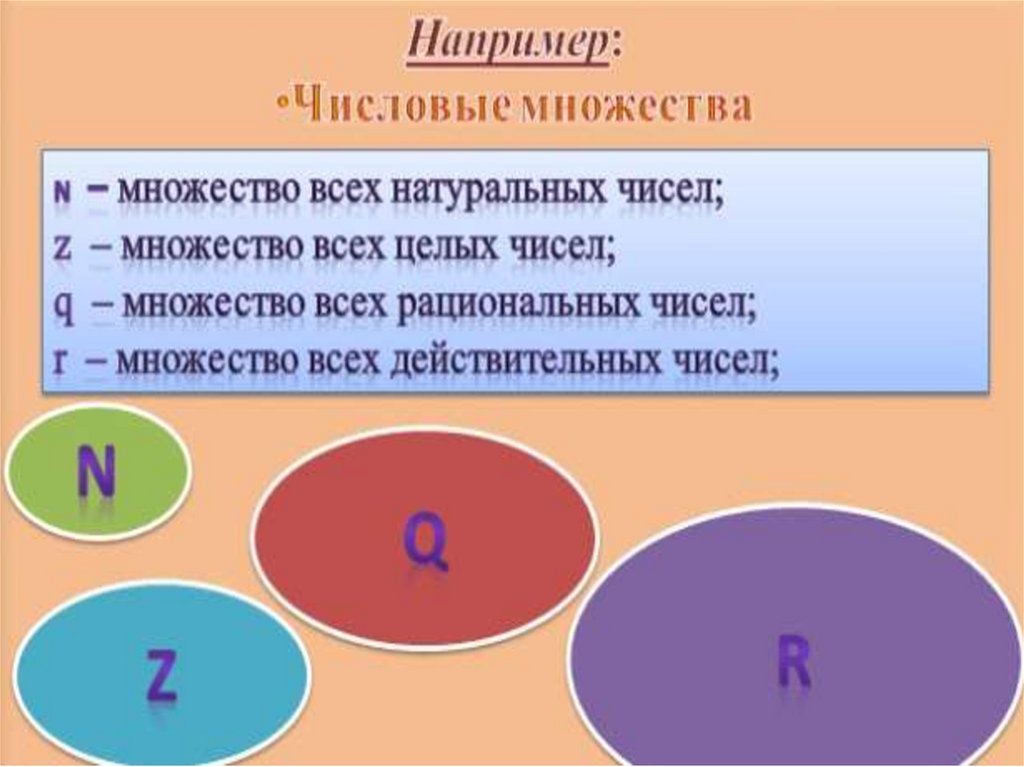
Числовые множества
Свойства множеств

4.

Множество, подмножество
«Множество есть многое, мыслимое
нами как единое»
основатель теории множеств – Георг Кантор
(1845—1918) — немецкий математик, логик,
теолог, создатель теории бесконечных
множеств, оказавшей определяющее влияние
на развитие математических наук на рубеже
19— 20 вв.

5.

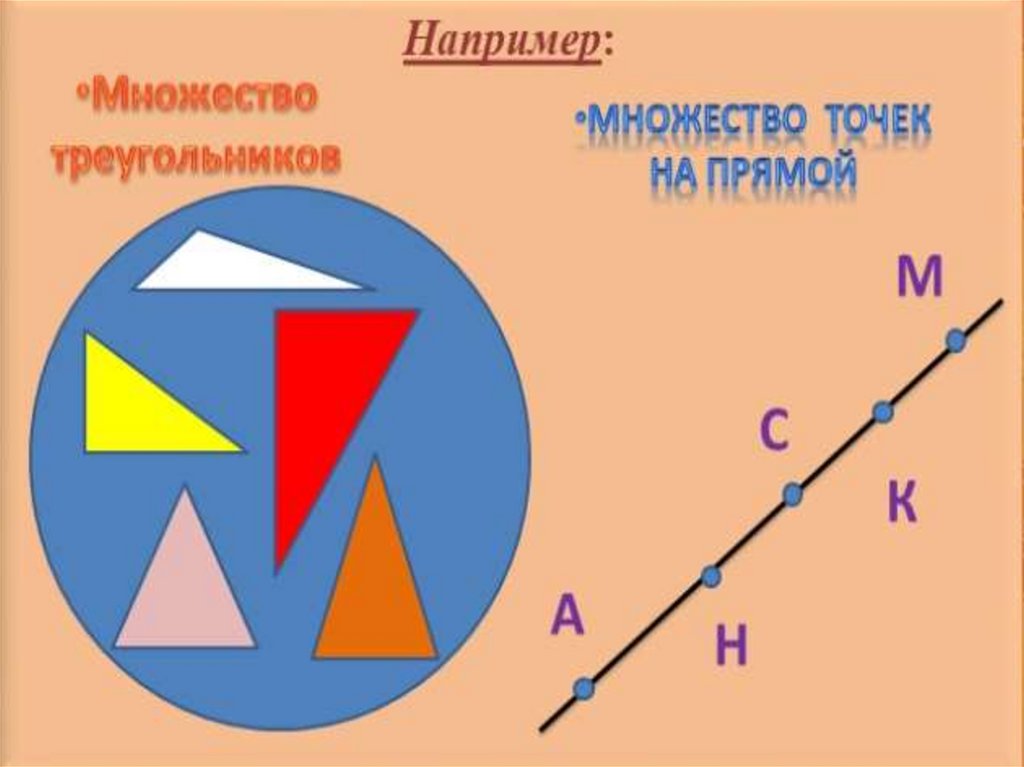
Примеры множеств из окружающего мира
Например, множество дней
недели состоит из элементов:
понедельник, вторник, среда,
четверг, пятница, суббота,
воскресенье.
Множество месяцев
– из элементов:
январь, февраль,
март, апрель, май,
июнь, июль,
август, сентябрь,
октябрь, ноябрь,
декабрь.

6.

7.

8.

Множество – это совокупность объектов,
объединённых каким-либо признаком, свойством
Множество можно задать одним из
двух способов:
1. Можно
явно
перечислить
все
элементы множества. (Н-р, дни
недели)
2. Можно описать множество, т.е.
указать
признак,
которым
обладают все элементы множества
(кубик с цифрами 1,2,3,4,5,6)

9.

Условные обозначения
Множества:
Заглавные буквы латинского алфавита или их сочетание: N,Z,
GR,…
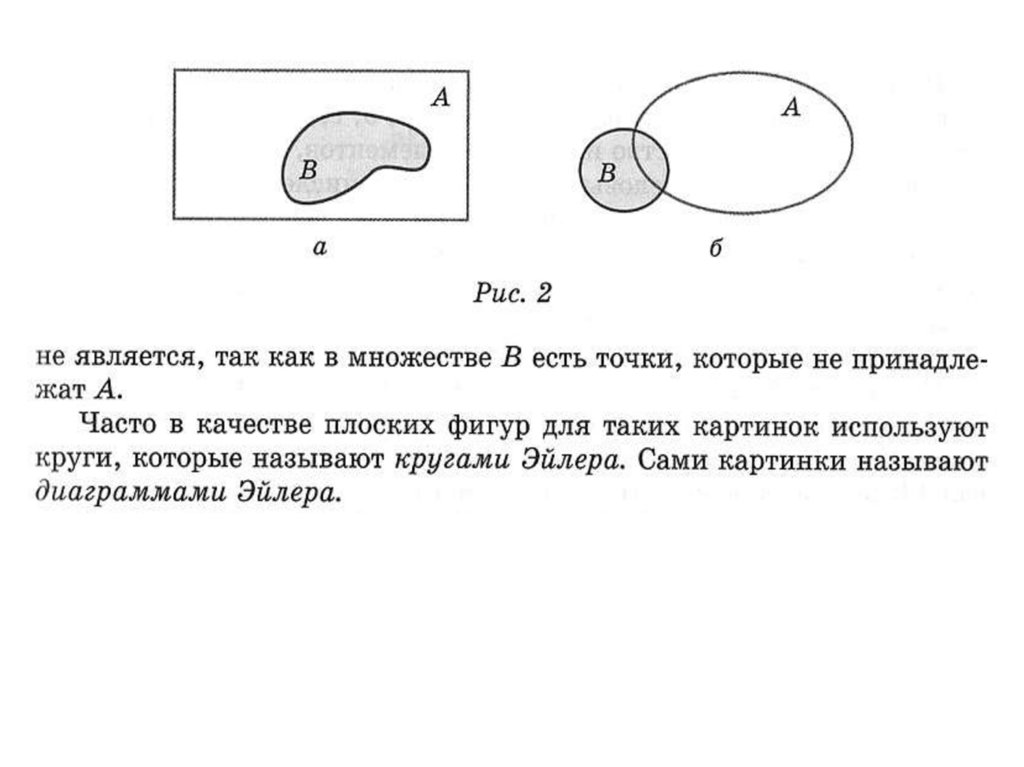
Графическое изображение –круги Эйлера , диаграммы
Венна
Элементы множества:
строчные буквы латинского алфавита: a, b, c,…
натуральное изображение элемента множества: 5, лисица,
……
Принадлежность элементов множеству:
«а принадлежит множеству А» - а ∈ А
«а не принадлежит множеству А» - а ∉ А
,

10.

Чтобы указать, что некоторый
элемент принадлежит множеству,
используют значок
Например:
6
А, читается « 6 принадлежит А»
7
А, читается «7 не принадлежит А»

11.

12.

13.

14.

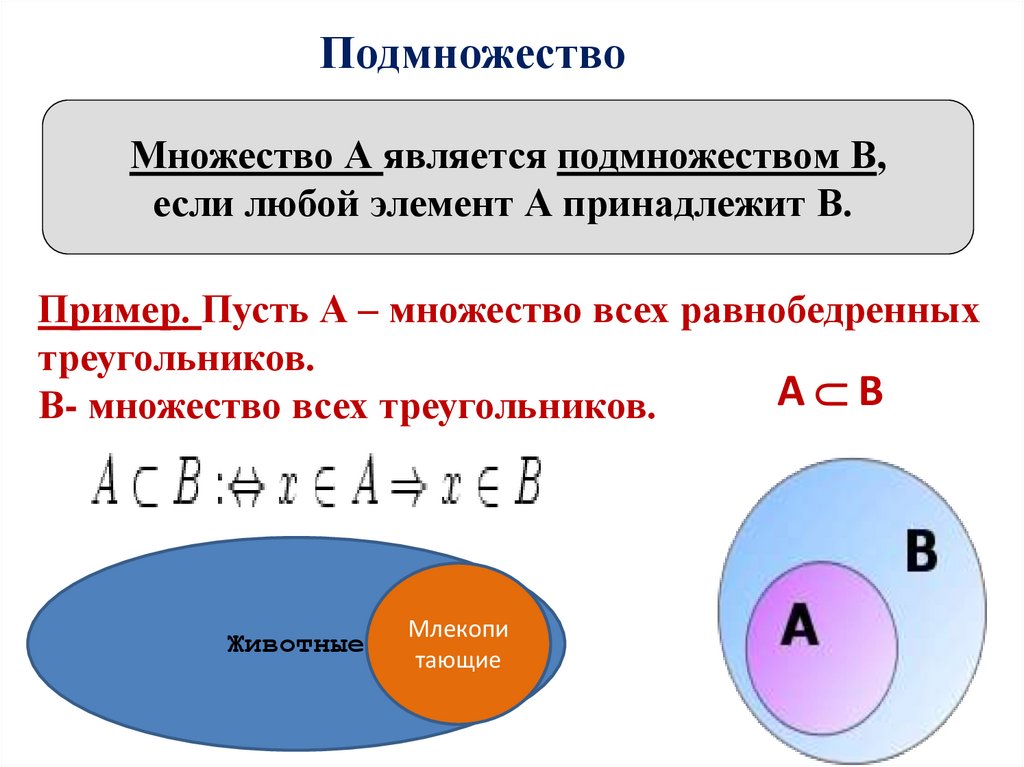
Подмножество
Множество А является подмножеством В,
если любой элемент А принадлежит В.
Пример. Пусть А – множество всех равнобедренных
треугольников.
А В
В- множество всех треугольников.
Животные
Млекопи
тающие

15.

16.

17.

Равные множества
Рассмотрим 2 множества:
a
А={a, b, c, d, e}
d
В={c, d, a, b, e}
c
b
e
Эти множества пересекаются, причем каждый
элемент множества А является элементом множества В (А ⊂ В), и
наоборот, каждый элемент множества В является элементом
множества А (В ⊂ А).
Множества А и В называются
, если А ⊂ В и В ⊂ А
А = В
Два множества A и B будут равны, если каждый
элемент A будет также являться элементом B, и
каждый элемент множества B будет также являться
элементом A:
А=В x | x A x B

18.

Пустое множество – это множество
которое не содержит элементов.
Пустое
множество
является
подмножеством любого множества
Любое множество
является
подмножеством самого
себя.
Пустое множество

19.

20.

Упражнения
№1
Какое множество задано путем
перечисления данных элементов?
А={0,1,2,3,4,5,6,7,8,9}
В={А,Е,И,О,У,Э,Ю,Я}
№2
Задайте множество крокодилов,
летящих в небе.

21.

Приложение к уроку 8
Дата:
Домашнее задание №8
Выполнить:
№3.