4.37M

Category:

physics

Lecture 8

1.

Capacitors and Inductors
OEk 1115 - Fundamentals of Electronics
Lecture 8

2.

Outline
Active vs. Passive Electronic Components
Capacitor
Series Capacitors
Parallel Capacitors
Inductor
Series Inductors
Parallel Inductors

Active vs. Passive Electronic Components
Active and passive electronic components are found in everyday items like lights,
sound systems, computers, phones, cars, and many more devices.
By definition, active components are found in every single electronic device.
Examples include any device with computing power (integrated circuits), devices
with a built-in battery or display, and LED lights (light-emitting diodes).
Examples of devices with passive components include incandescent light bulbs,
loudspeakers, sensors, microwaves, remote keyless entry systems, and antennas.

4.

Active components
Active components are semiconductor devices that consist of
semiconductor materials.
They supply electric power to the circuit or power gain in the circuit.
Common electronic devices are diodes and transistors, which perform
“active” operations like amplifying, rectifying, or converting supplied
current (signal).

5.

Passive components
Passive components are required electronic devices that perform
“passive” operations like consuming, storing, or releasing electric
power.
They can only absorb electrical energy and dissipate it in the form of
heat or store it in a magnetic or electric field.
They cannot provide electric power or power amplification in an
electric circuit.
Common passive components include resistors, capacitors, and coils.

6.

Active vs. Passive Electronic Components
Active Component
Passive Component
An active device transforms and injects power or
energy into a circuit.
A passive device uses power or energy from a
circuit.
Examples: Diodes, transistors, SCR, integrated
circuits, etc.
Examples: Resistors, capacitors, inductors, etc.
They are capable of providing power gain
(amplifier).
They are incapable of providing power gain.
They are energy donors.
They are energy acceptors.
They can control the flow of current.
They cannot control the flow of current.

7.

Capacitor
A capacitor is a passive electrical component that stores electrical charge and
has the property of capacitance.
A capacitor is an electrical device constructed of two parallel conductive plates
separated by an insulating material called the dielectric.
Connecting leads are attached to the parallel plates.

8.

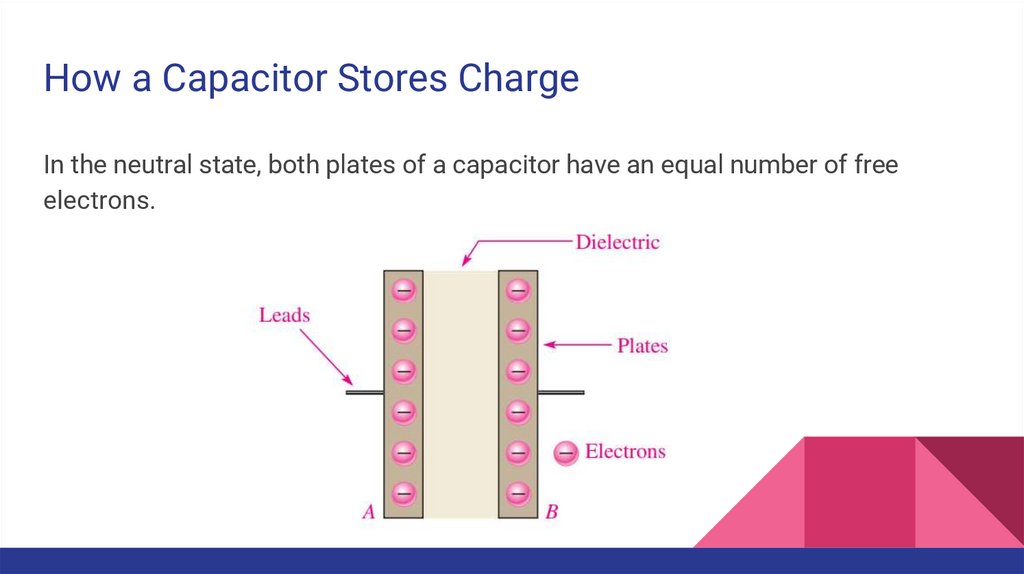
How a Capacitor Stores Charge
In the neutral state, both plates of a capacitor have an equal number of free
electrons.

9.

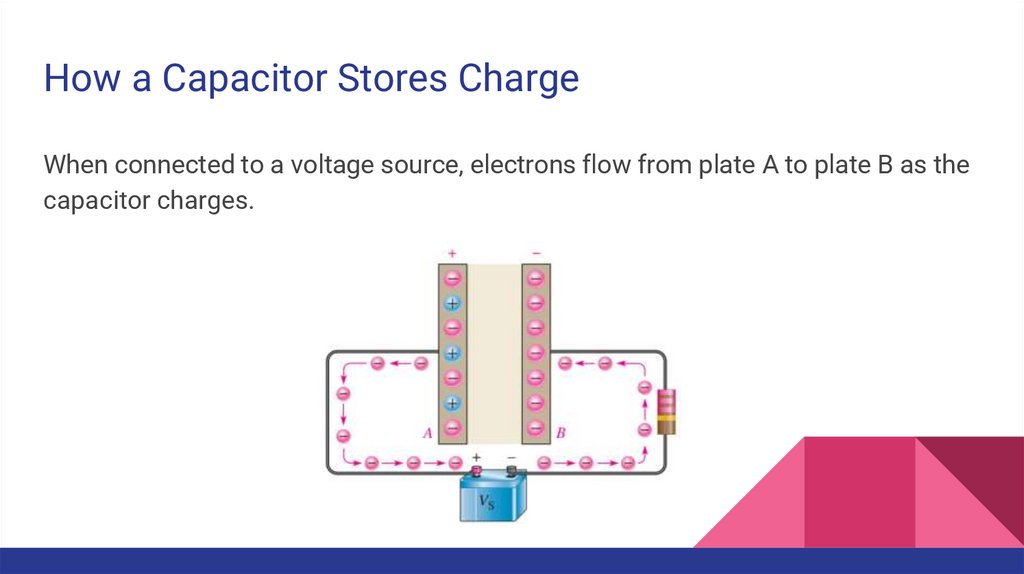
How a Capacitor Stores Charge
When connected to a voltage source, electrons flow from plate A to plate B as the
capacitor charges.

10.

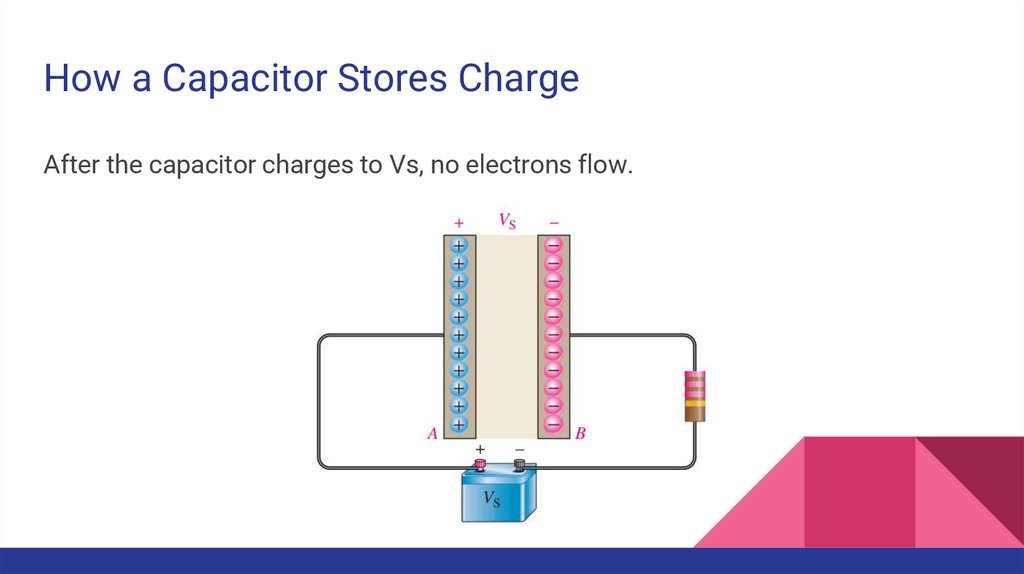
How a Capacitor Stores Charge
After the capacitor charges to Vs, no electrons flow.

11.

How a Capacitor Stores Charge
Ideally, the capacitor retains charge when disconnected from the voltage source.

12.

Capacitance
Capacitance is a measure of a capacitor’s ability to store charge.
The more charge per unit of voltage that a capacitor can store, the greater its capacitance:
C is capacitance,
Q is charge,
and V is voltage.
The farad (F) is the basic unit of capacitance. Recall that the coulomb (C) is the unit of electrical charge.
One farad is the amount of capacitance when one coulomb of charge is stored with one volt across the plates.

13.

Capacitance
Example.
a) C = Q / V = 50 / 10 = 5 microF
b) Q = C * V = 2,2 * 100 = 220 microC
c) V = Q / C = (2 * 10(-6)) / (100 * 10(-12)) = 2 / (100 * 10(-6)) = 2 / (0,1 * 10(-3)) = 20 000 V
V = 20 KV

14.

Capacitance
Solution.

15.

How a Capacitor Stores Energy
A capacitor stores energy in an electric field that is
established by the opposite charges stored on the two
plates.
The electric field is represented by lines of force between
the positive and negative charges and is concentrated
within the dielectric.
The plates in have acquired a charge because they are
connected to a battery. This creates an electric field
between the plates, which stores energy.

16.

Types of Capacitors
Capacitors normally are classified according to the type of dielectric material.
The most common types of dielectric materials are mica, ceramic, plastic-film, and electrolytic
(aluminum oxide and tantalum oxide).

17.

Series Capacitors
The total capacitance of a series connection of capacitors is less than the
individual capacitance of any of the capacitors.
Capacitors in series divide voltage across them in proportion to their capacitance.

18.

Series Capacitors
By Kirchhoff’s voltage law, which applies to capacitive circuits as well as to
resistive circuits, the sum of the capacitor voltages equals the source voltage.
If only two Capacitors in series:

19.

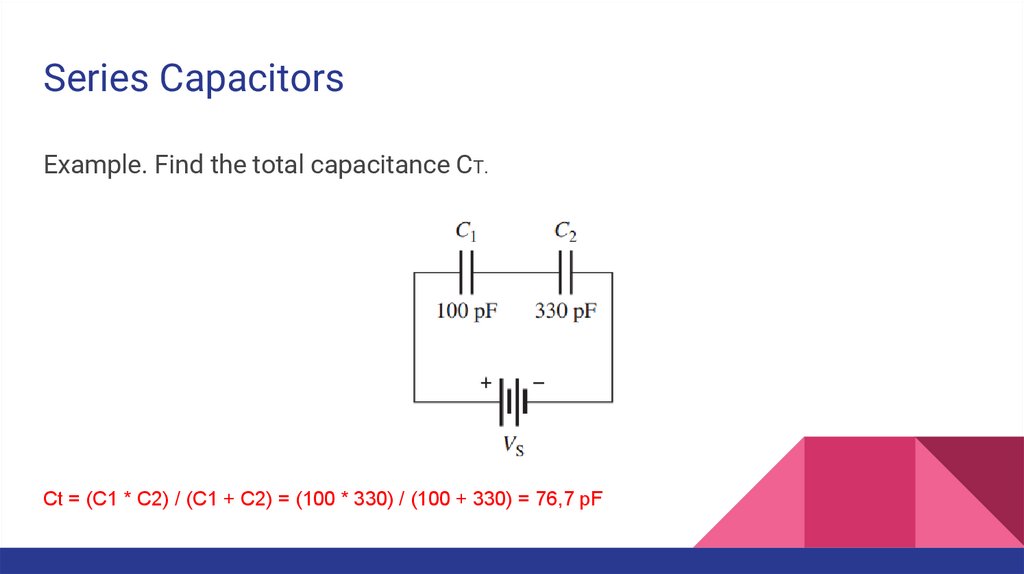
Series Capacitors
Example. Find the total capacitance CT.
Ct = (C1 * C2) / (C1 + C2) = (100 * 330) / (100 + 330) = 76,7 pF

20.

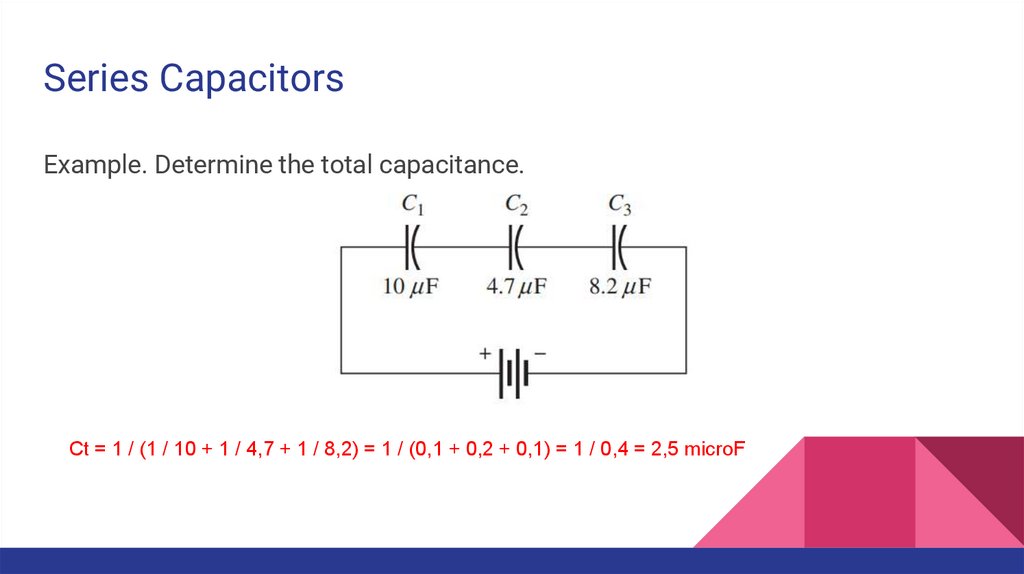
Series Capacitors
Example. Determine the total capacitance.
Ct = 1 / (1 / 10 + 1 / 4,7 + 1 / 8,2) = 1 / (0,1 + 0,2 + 0,1) = 1 / 0,4 = 2,5 microF

21.

Capacitor Voltages
The voltage across each capacitor in a series connection depends on its
capacitance value according to the formula V = Q/C.
You can determine the voltage across any individual capacitor in series with the
following formula:
The largest-value capacitor in a series connection will have the smallest voltage
across it. The smallest-value capacitor will have the largest voltage across it.

22.

Capacitor Voltages
Example. Find the voltage across each capacitor.
Ct = 1 / (1 / 0,1 + 1 / 0,47 + 1 / 0,22) = 1 / (10 + 2 + 5) = 1 / 17 = 0,06 microF
V1 = (Ct / C1) * Vs = (0,06 / 0,1) * 25 = 15 V
V2 = (Ct / C2) * Vs = (0,06 / 0,47) * 25 = 3,2 V
V3 = (Ct / C3) * Vs = (0,06 / 0,22) * 25 = 6,8 V

23.

Capacitor Voltages
Solution.

24.

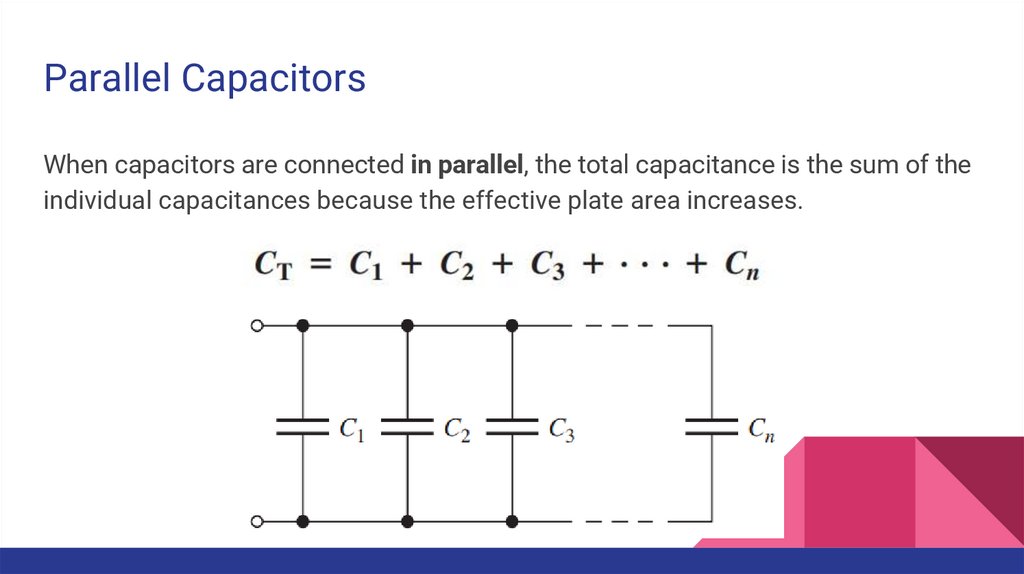
Parallel Capacitors
When capacitors are connected in parallel, the total capacitance is the sum of the
individual capacitances because the effective plate area increases.

25.

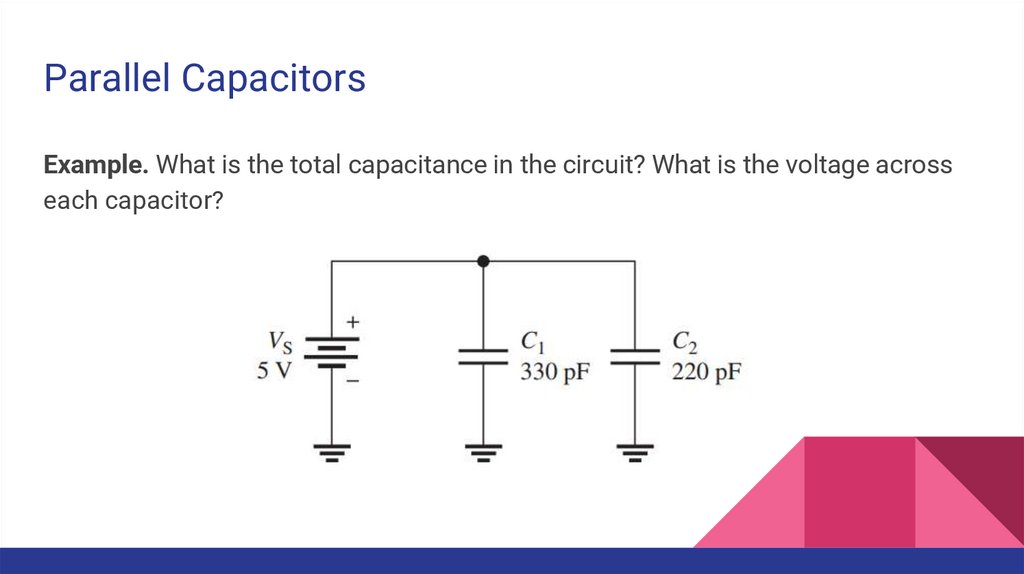
Parallel Capacitors
Example. What is the total capacitance in the circuit? What is the voltage across
each capacitor?

26.

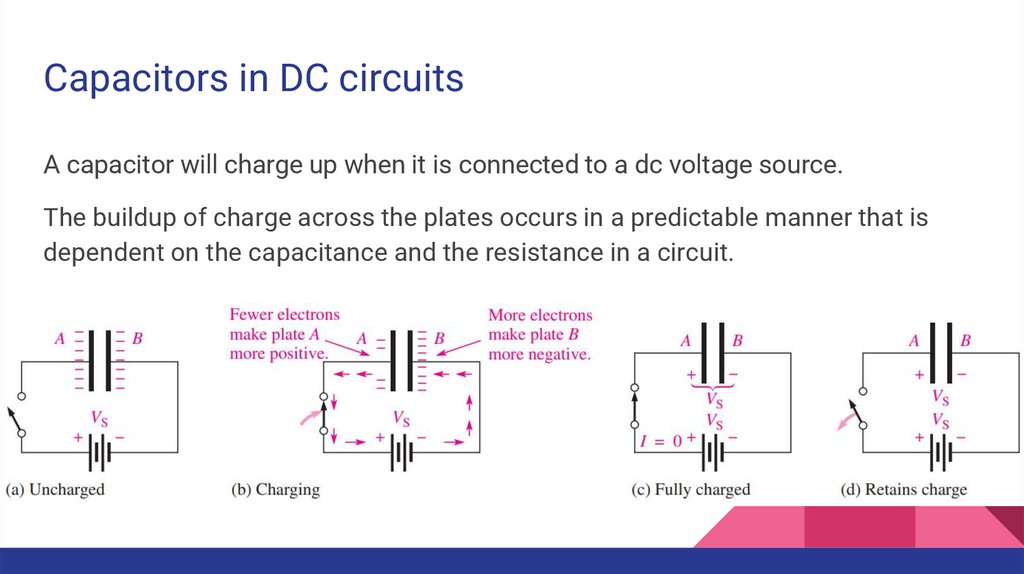
Capacitors in DC circuits
A capacitor will charge up when it is connected to a dc voltage source.
The buildup of charge across the plates occurs in a predictable manner that is
dependent on the capacitance and the resistance in a circuit.

27.

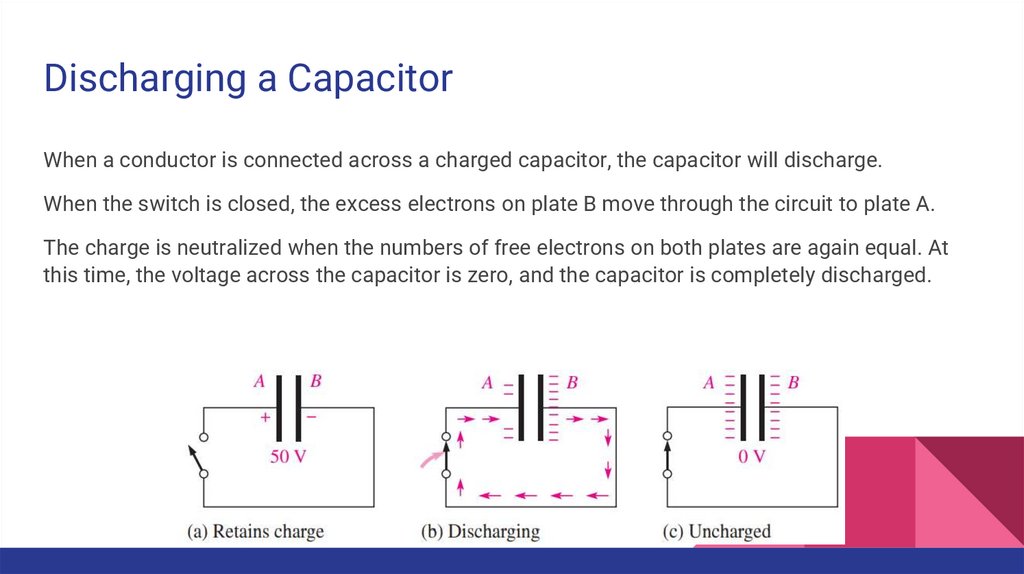
Discharging a Capacitor
When a conductor is connected across a charged capacitor, the capacitor will discharge.
When the switch is closed, the excess electrons on plate B move through the circuit to plate A.
The charge is neutralized when the numbers of free electrons on both plates are again equal. At
this time, the voltage across the capacitor is zero, and the capacitor is completely discharged.

28.

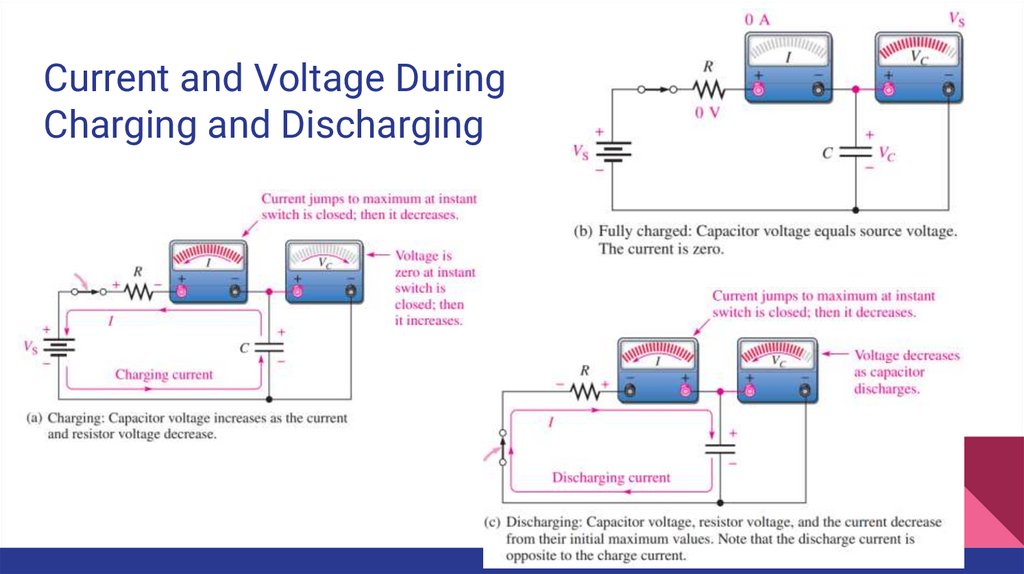
Current and Voltage During
Charging and Discharging

29.

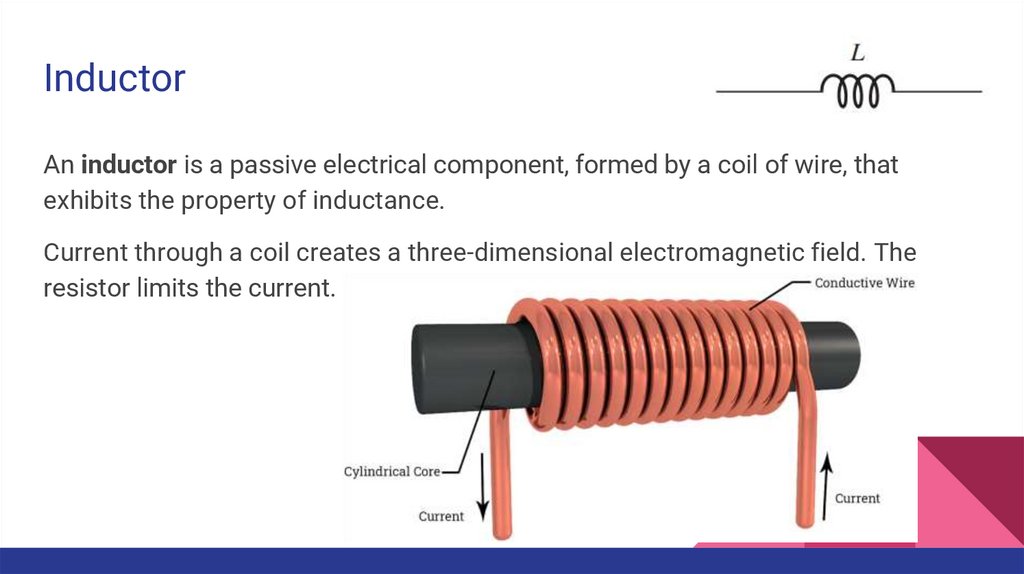
Inductor
An inductor is a passive electrical component, formed by a coil of wire, that
exhibits the property of inductance.
Current through a coil creates a three-dimensional electromagnetic field. The
resistor limits the current.

30.

Inductor
When a length of wire is formed into a coil and becomes an
inductor.
Current through the coil produces an electromagnetic field.
The magnetic lines of force around each loop (turn) in the
winding of the coil effectively add to the lines of force around
the adjoining loops, forming a stronger magnetic field within
and around the coil.
The net direction of the total magnetic field creates a north
and a south pole.

31.

Inductance
When there is current through an inductor, an electromagnetic field is established.
When the current changes, the electromagnetic field also changes.
An increase in current expands the field, and a decrease in current reduces it.
Therefore, a changing current produces a changing electromagnetic field around the
inductor (also known as coil and in some applications, choke).
In turn, the changing electromagnetic field causes an induced voltage across the coil in
a direction to oppose the change in current.
This property is called selfinductance but is usually referred to as simply inductance,
symbolized by L.

32.

Henry
The henry, symbolized by H, is the basic unit of inductance.
The inductance of a coil is one henry when current through the coil, changing at the
rate of one ampere per second, induces one volt across the coil.
An inductor stores energy in the magnetic field created by the current.
When current (I) is in amperes and inductance (L) is in henries, the energy (W) is in
joules.

33.

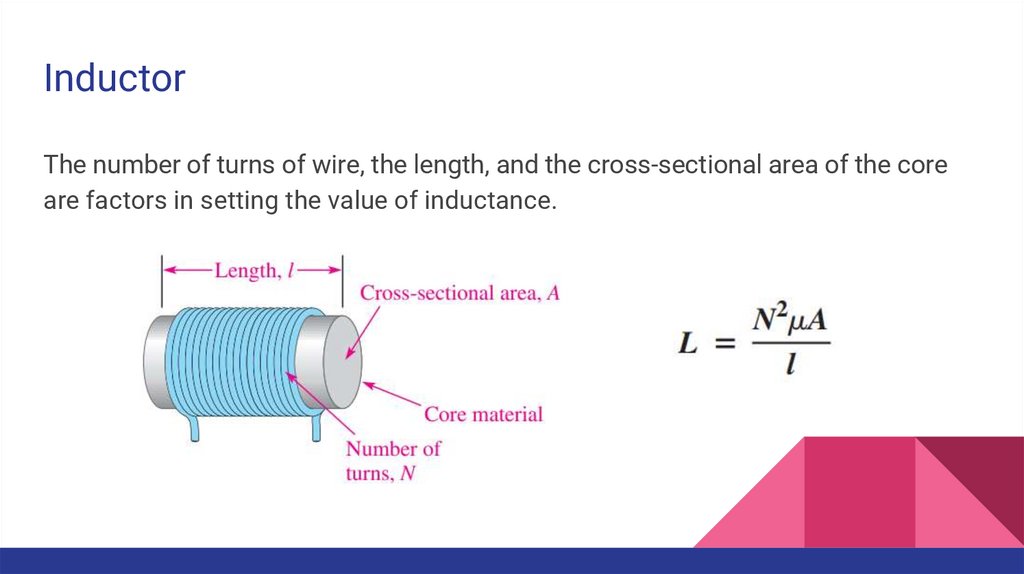
Inductor
The number of turns of wire, the length, and the cross-sectional area of the core
are factors in setting the value of inductance.

34.

Faraday’s and Lenz’s Laws
Faraday’s Law:
The amount of voltage induced in a coil is directly proportional to the rate of
change of the magnetic field with respect to the coil.
Lenz’s Law:
When the current through a coil changes and an induced voltage is created as a
result of the changing magnetic field, the direction of the induced voltage is such
that it always opposes the change in current.

35.

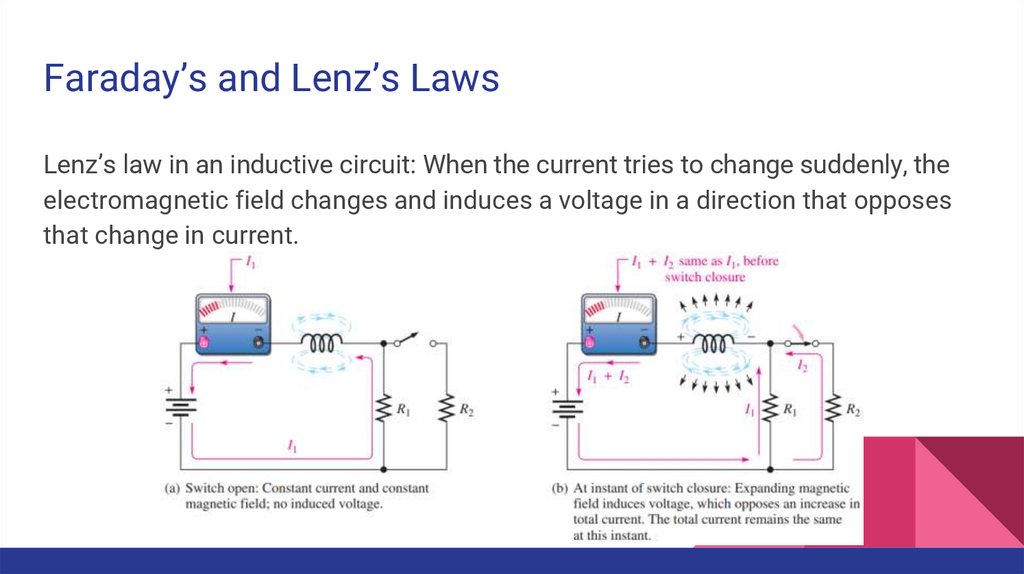
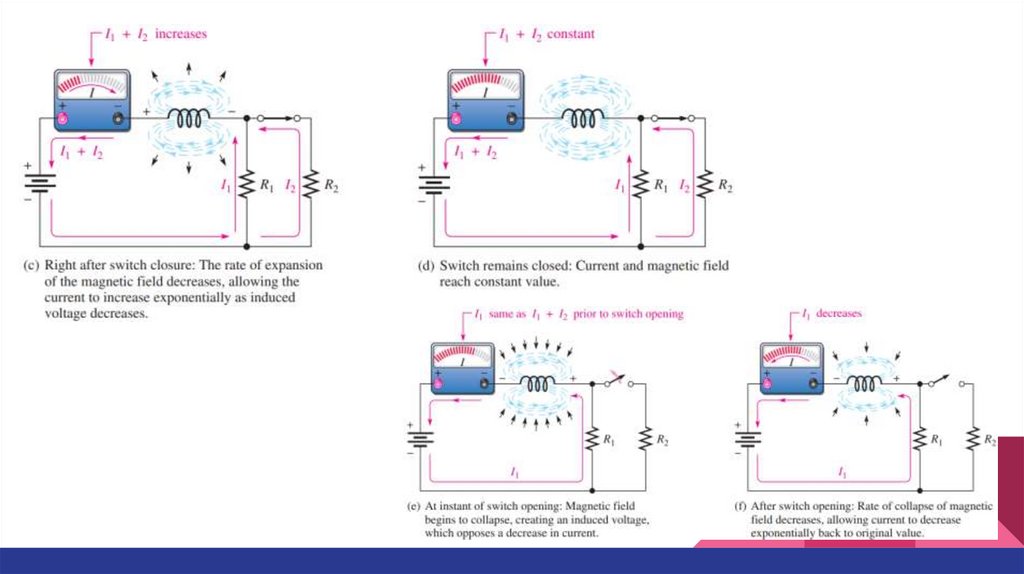
Faraday’s and Lenz’s Laws
Lenz’s law in an inductive circuit: When the current tries to change suddenly, the
electromagnetic field changes and induces a voltage in a direction that opposes
that change in current.

36.

37.

Types of Inductors
Inductors are made in a variety of shapes and sizes. Basically, they fall into two
general categories: fixed and variable.
Inductors normally are classified according to the type of core material.

38.

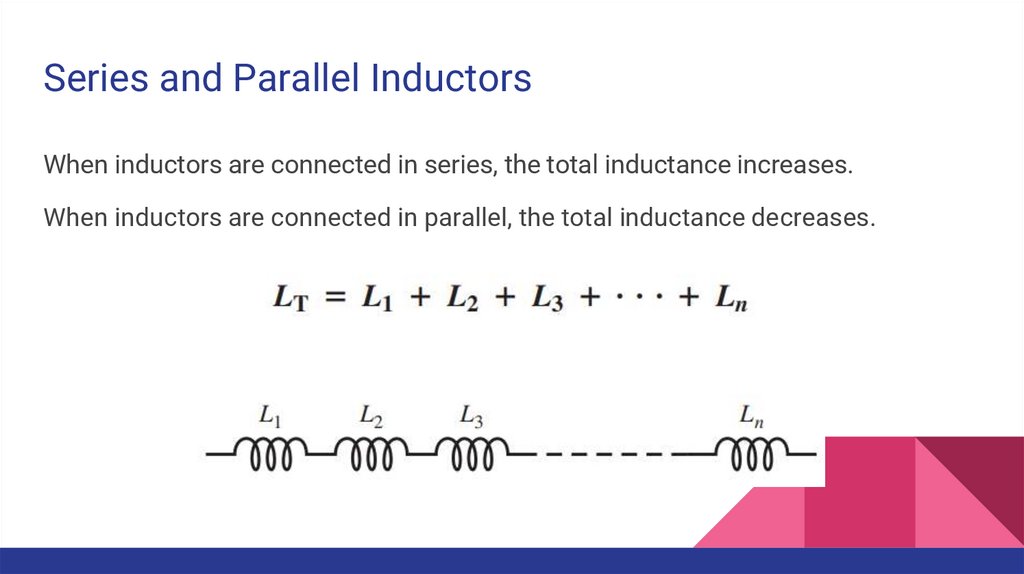
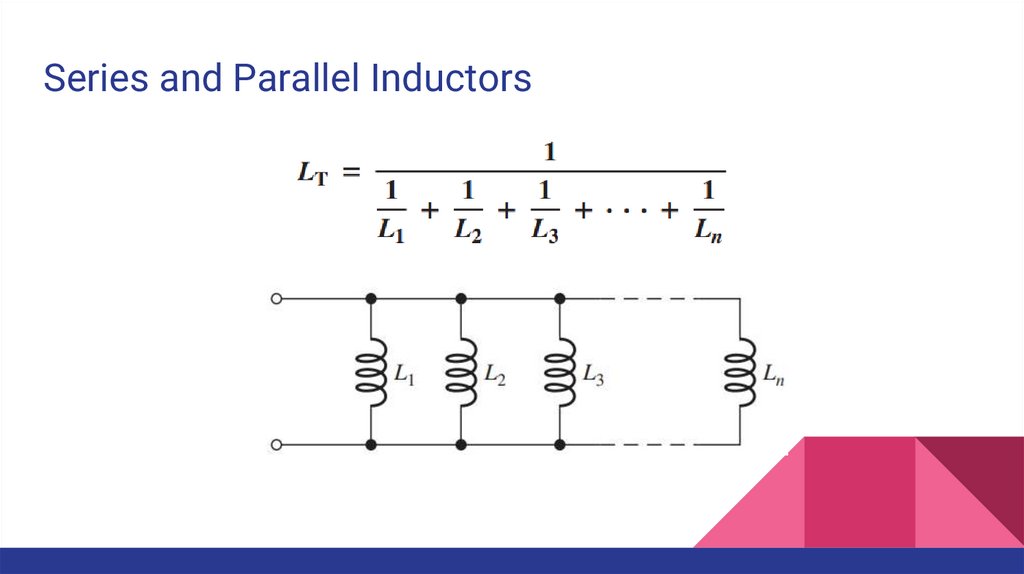
Series and Parallel Inductors
When inductors are connected in series, the total inductance increases.
When inductors are connected in parallel, the total inductance decreases.

39.

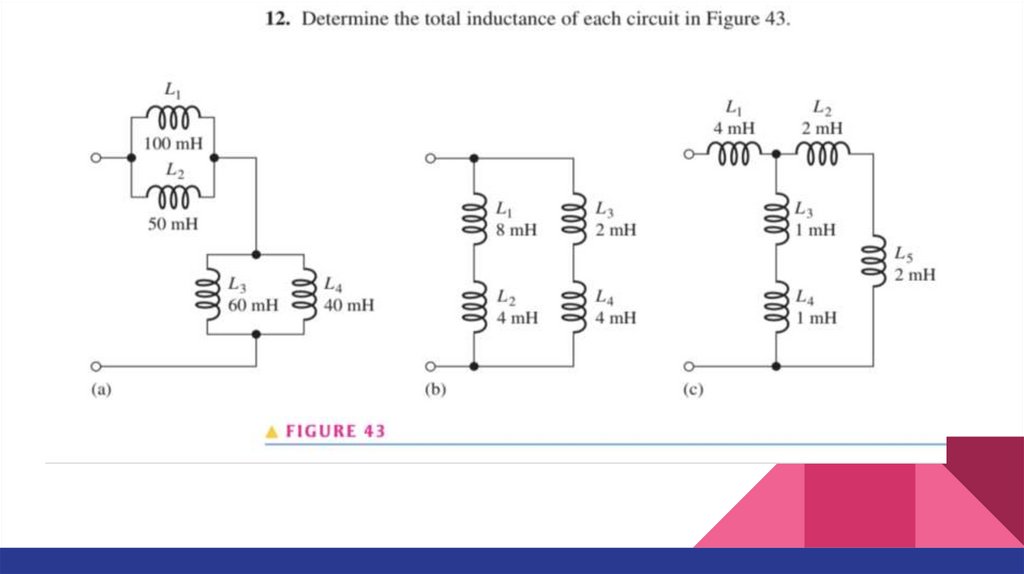
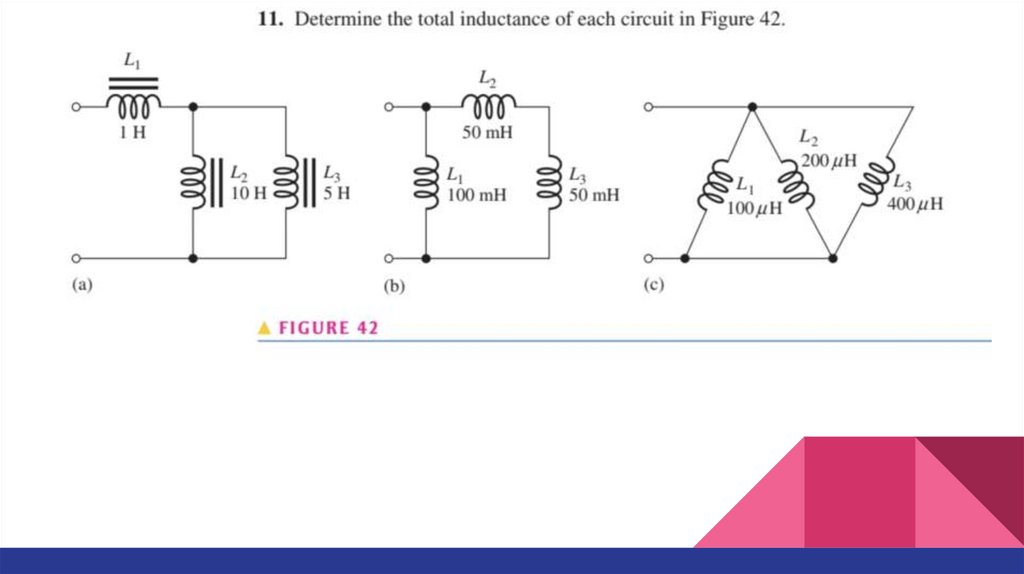
Series and Parallel Inductors
Example. Determine the total inductance for each of the series connections.

40.

Series and Parallel Inductors

41.

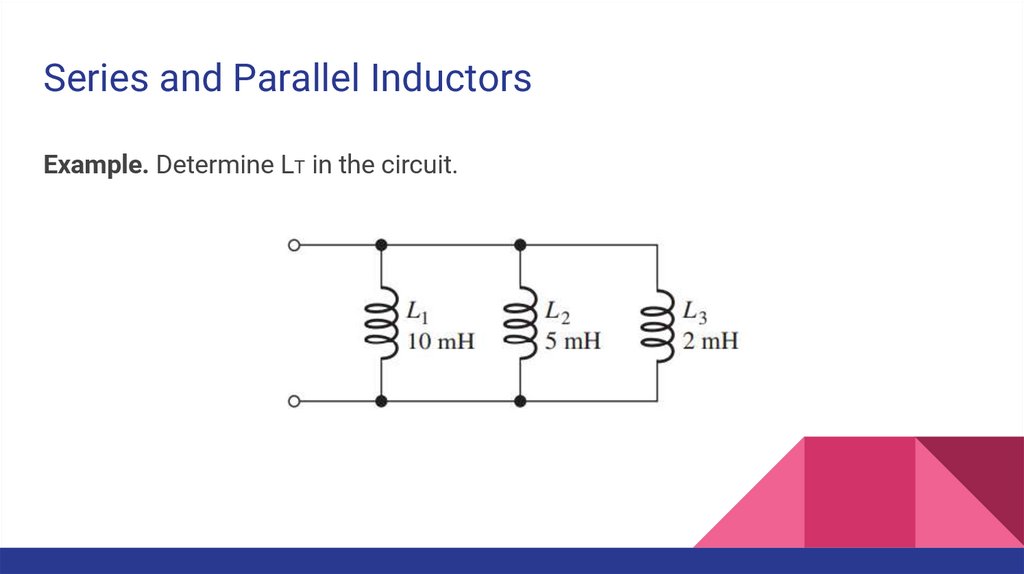
Series and Parallel Inductors
Example. Determine LT in the circuit.

42.

a)
b)
c)
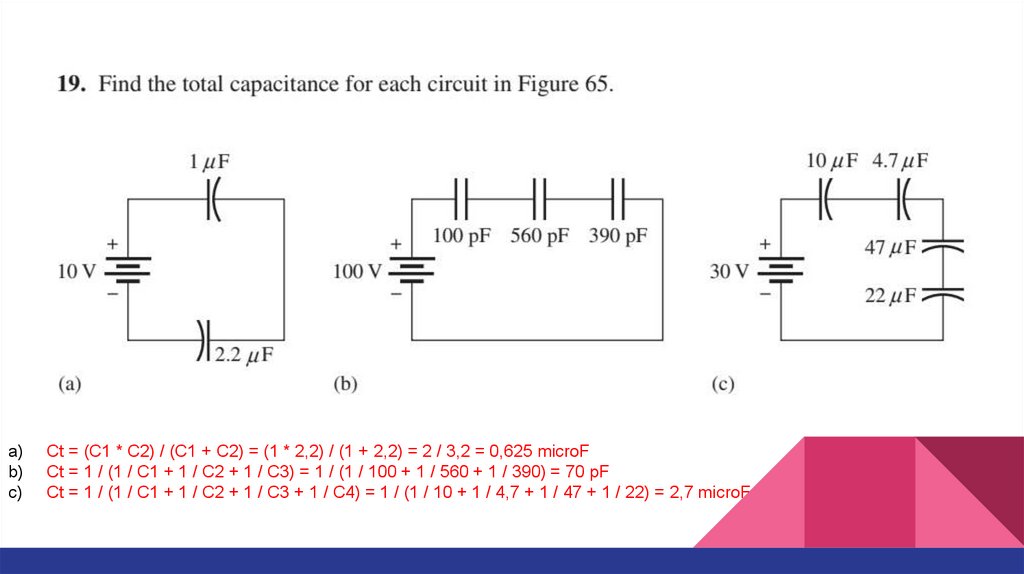
Ct = (C1 * C2) / (C1 + C2) = (1 * 2,2) / (1 + 2,2) = 2 / 3,2 = 0,625 microF
Ct = 1 / (1 / C1 + 1 / C2 + 1 / C3) = 1 / (1 / 100 + 1 / 560 + 1 / 390) = 70 pF
Ct = 1 / (1 / C1 + 1 / C2 + 1 / C3 + 1 / C4) = 1 / (1 / 10 + 1 / 4,7 + 1 / 47 + 1 / 22) = 2,7 microF

43.

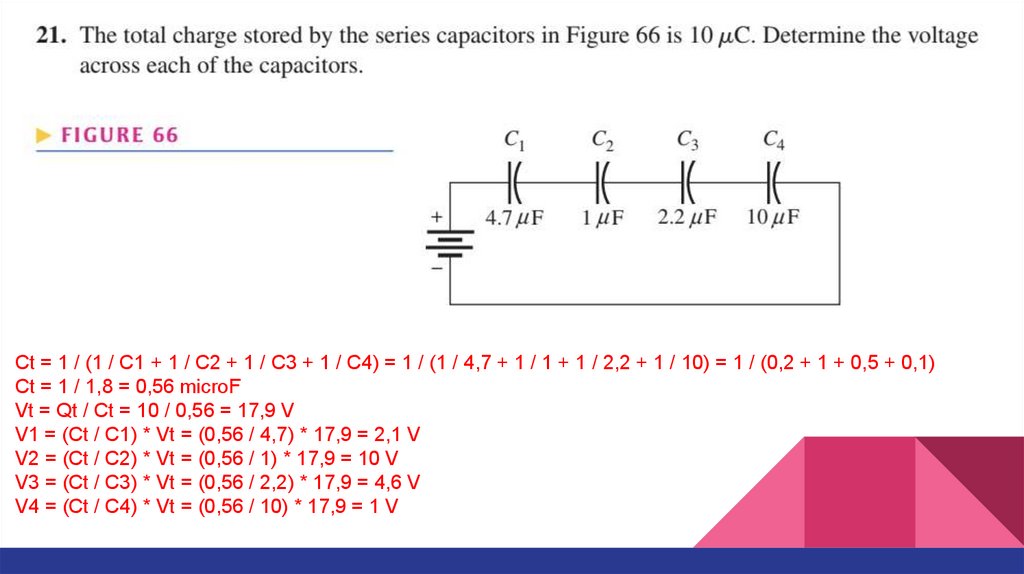
Ct = 1 / (1 / C1 + 1 / C2 + 1 / C3 + 1 / C4) = 1 / (1 / 4,7 + 1 / 1 + 1 / 2,2 + 1 / 10) = 1 / (0,2 + 1 + 0,5 + 0,1)
Ct = 1 / 1,8 = 0,56 microF
Vt = Qt / Ct = 10 / 0,56 = 17,9 V
V1 = (Ct / C1) * Vt = (0,56 / 4,7) * 17,9 = 2,1 V
V2 = (Ct / C2) * Vt = (0,56 / 1) * 17,9 = 10 V
V3 = (Ct / C3) * Vt = (0,56 / 2,2) * 17,9 = 4,6 V
V4 = (Ct / C4) * Vt = (0,56 / 10) * 17,9 = 1 V