Similar presentations:
Алгоритмы сортировки данных (продолжение)
1. 6-лекция: Алгоритмы сортировки данных (продолжение)
План:4. Улучшенные методы сортировок
1.
2.
3.
4.
5.
6.
Быстрая сортировка
Сортировка Шелла
Сортировка слиянием
Сортировка подсчетом
Цифровая сортировка
Пирамидальная сортировка
© ТУИТ, кафедра СПП
2. Быстрая сортировка
Относится к методам обменной сортировки. В основележит методика разделения ключей по отношению к
выбранному.
Разработана английским информатиком Чарльзом
Хоаром в 1960 году в Московском университете, где он
обучался
компьютерному
переводу
и
занимался
разработкой русско-английского разговорника.
В то время словарь хранился на магнитной ленте, и
если упорядочить все слова в тексте, их переводы можно
получить за один прогон ленты.
Наиболее популярный алгоритм сортировки.
В стандартной библиотеке С++ реализация называется
qsort.
© ТУИТ, кафедра СПП
3. Быстрая сортировка
Алгоритм:1) выбрать элемент, называемый опорным. Можно выбирать
различными способами. Например, средний.
2) сравнить все остальные элементы с опорным, на
основании сравнения разбить множество на – «меньшие
опорного» и «большие опорного», расположить их в порядке
меньшие – большие.
3) повторить рекурсивно для «меньших» и «больших». Базой
рекурсии являются наборы, состоящие из одного или двух
элементов. Первый возвращается в исходном виде, во втором,
при необходимости, сортировка сводится к перестановке двух
элементов.
Поскольку на каждом следующем уровне рекурсии длина
обрабатываемого отрезка массива уменьшается, по меньшей
мере, на единицу, терминальная ветвь рекурсии будет
достигнута
обязательно
и
обработка
гарантированно
завершится.
© ТУИТ, кафедра СПП
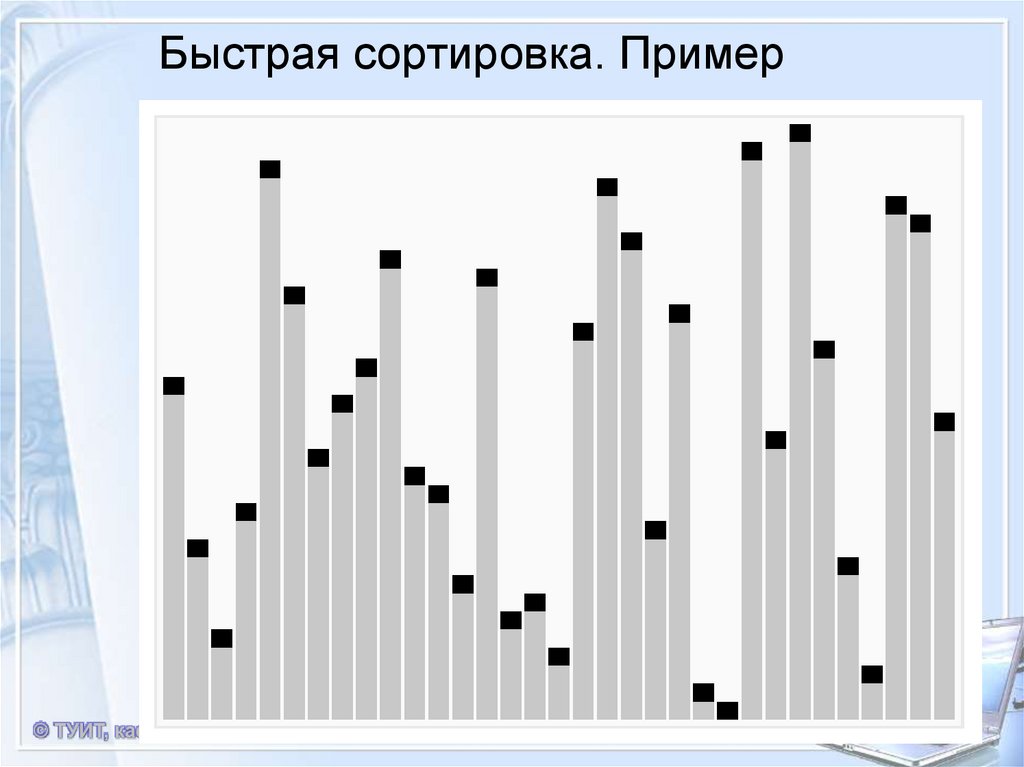
4. Быстрая сортировка. Пример
© ТУИТ, кафедра СПП5. Быстрая сортировка. Пример
© ТУИТ, кафедра СПП6. Быстрая сортировка. Оценка эффективности
Лучший случай. В каждой итерации массивразделяется на два равных по величине подмассива. Это
дает наименьшее время сортировки.
Худший случай. В каждой итерации массив
разделяется на вырожденный подмассив из одного
опорного элемента и на подмассив из всех остальных
элементов. Такое может произойти, если в качестве
опорного на каждом этапе будет выбран элемент либо
наименьший, либо наибольший из всех обрабатываемых.
О(n logn)
© ТУИТ, кафедра СПП
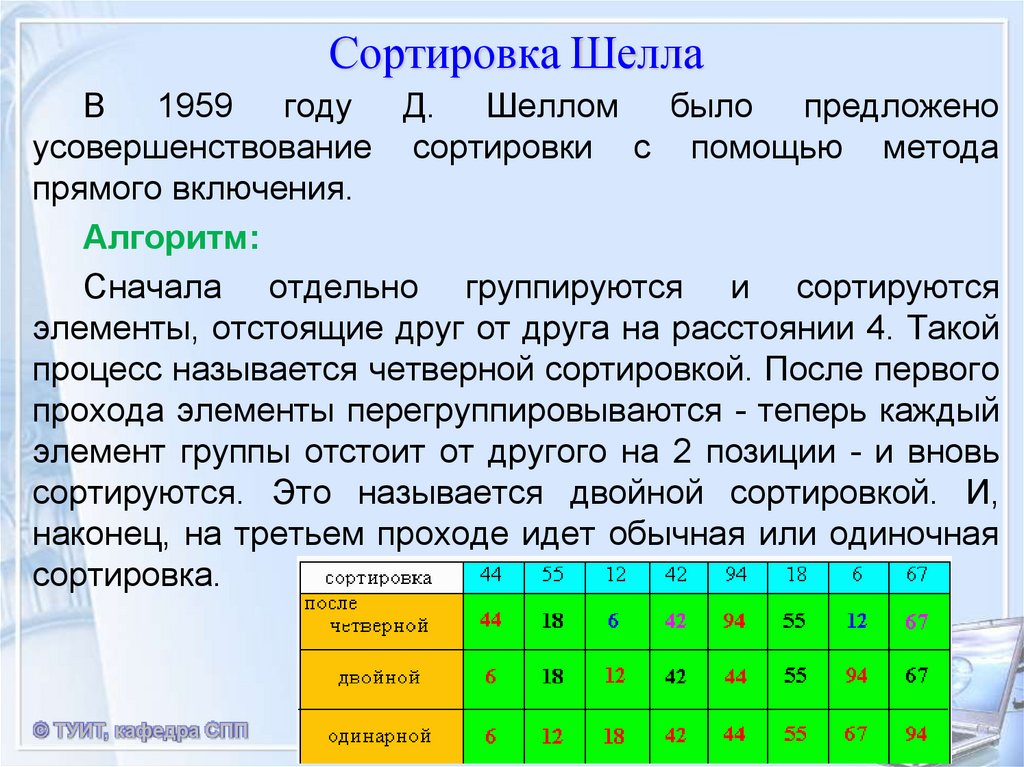
7. Сортировка Шелла
В 1959 году Д. Шеллом было предложеноусовершенствование сортировки с помощью метода
прямого включения.
Алгоритм:
Сначала отдельно группируются и сортируются
элементы, отстоящие друг от друга на расстоянии 4. Такой
процесс называется четверной сортировкой. После первого
прохода элементы перегруппировываются - теперь каждый
элемент группы отстоит от другого на 2 позиции - и вновь
сортируются. Это называется двойной сортировкой. И,
наконец, на третьем проходе идет обычная или одиночная
сортировка.
© ТУИТ, кафедра СПП
8. Сортировка Шелла
Не доказано, какие расстояния дают наилучшийрезультат, но они не должны быть множителями один
другого.
Д. Кнут предлагает такую последовательность шагов (в
обратном порядке): 1, 3, 7, 15, 31, …
То есть: h m-1 = h m + 1, t = log2n - 1.
При такой организации алгоритма его эффективность
имеет порядок O ( n1.2)
Р.Седжвик предлагает такую последовательность шагов
9 * 2 s 9 * 2 s / 2 1, если s нечетно
inc[ s ]
8 * 2 s 6 * 2( s 1) / 2 1, если s четно
Средний случай - O(n7/6),
Худший случай - O(n4/3).
© ТУИТ, кафедра СПП
Если 3*inc[s]>n, тогда
шагом будет inc[s-1].
9.
Сортировка Шелла0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 10 3 14 21 36 1
8 24 38 50 31 42 53 16 27 51 59 33 44
step=7
step=3
1
8
3
4 10 36 14 21 24 27 44 31 33 50 16 38 51 59 42 53
1
4
3
8 10 21 14 27 16 31 24 36 33 38 42 50 44 53 51 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59
step=2
step=1
© ТУИТ, кафедра СПП
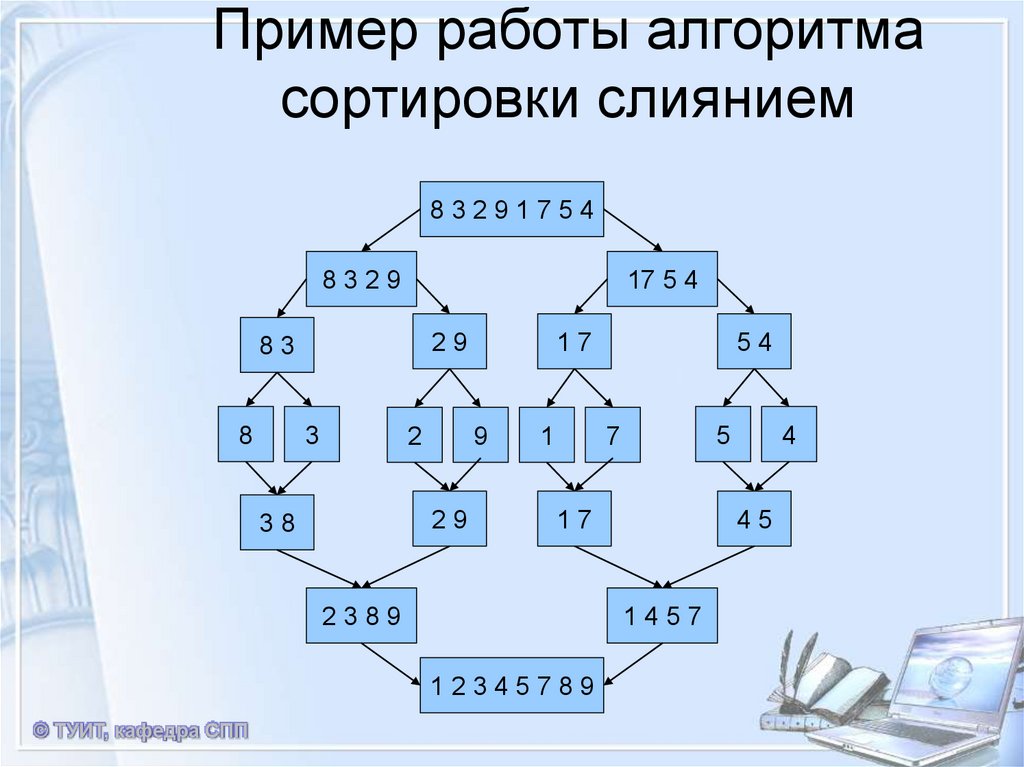
10. Сортировка слиянием
Этапы решения задачи сортировки:1) Сортируемый массив разбивается на две части
меньшего размера;
2) Каждая из получившихся частей сортируется
отдельно;
3) Два упорядоченных массива меньшего размера
соединяются в один.
Рекурсивное разбиение задачи на меньшие
происходит до тех пор, пока размер массива не
достигнет единицы (любой массив длины 1 можно
считать упорядоченным).
© ТУИТ, кафедра СПП
11. Сортировка слиянием применительно к случайным точкам
© ТУИТ, кафедра СПП12. Пример работы алгоритма сортировки слиянием
832917548329
17 5 4
29
83
8
3
2
9
29
38
17
1
5
7
17
2389
4
45
1457
12345789
© ТУИТ, кафедра СПП
54
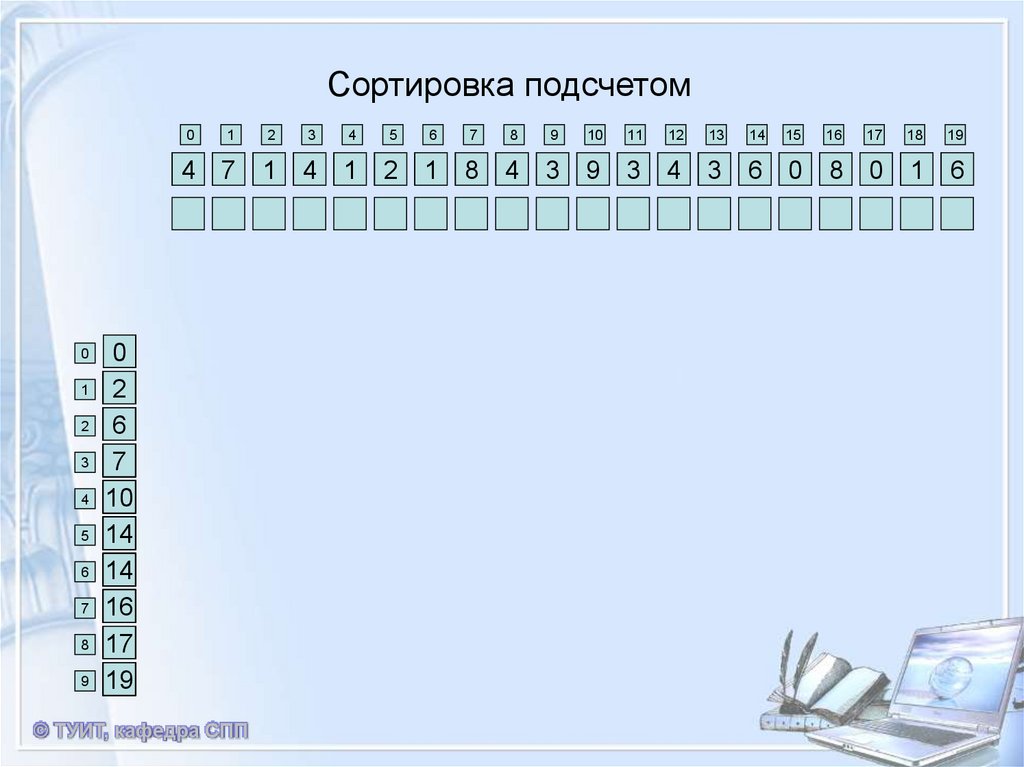
13. Сортировка подсчетом
Сортировка подсчётом — алгоритм сортировки, вкотором используется диапазон чисел
сортируемого массива (списка) для подсчёта
совпадающих элементов.
Применение сортировки подсчётом целесообразно
лишь тогда, когда сортируемые числа имеют (или
их можно отобразить в) диапазон возможных
значений, который достаточно мал по сравнению с
сортируемым множеством, например, миллион
натуральных чисел меньших 1000.
© ТУИТ, кафедра СПП
14.
Сортировка подсчетом0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
4
7
1
4
1
2
1
8
4
3
9
3
4
3
6
0
8
0
1
6
2
1
0
1
6
5
4
3
2
2
1
7
6
3 10
3
9
8
7
4 10
14
13
12
11
4
5 14
0
6 14
16
15
2
7 16
17
1
8 17
19
18
2
9 19
20
1
0
© ТУИТ, кафедра СПП
15.
Программа для сортировки подсчетомpublic static void countSort (int[] src, int[] dest) {
// Предполагается, что все элементы src[i] из диапазона 0..15
int n = src.length;
// Длина массива
int[] count = new int[16];
// Массив для подсчета элементов
// 1. Подсчет
for (int i = 0; i < n; i++) {
count[src[i]]++;
}
// 2. Суммирование
for (int i = 1; i < 16; i++) {
count[i] += count[i-1];
}
// 3. Расстановка
for (int i = n-1; i >= 0; i--) {
dest[--count[src[i]]] = src[i];
}
}
© ТУИТ, кафедра СПП
16.
Цифровая сортировка4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 39 50 21 36
После сортировки по последней цифре:
10 50 51 31 1 21 42 3 33 53 4 14 24 44 16 36 27 8 59 39
После устойчивой сортировки по первой цифре:
1
3
4
© ТУИТ, кафедра СПП
8 10 14 16 21 24 27 31 33 36 39 42 44 50 51 53 59
17.
Программа для цифровой сортировкиpublic static void digitSort(int[] data) {
int n = data.length;
// Длина массива
int[] data2 = new int[n];
// Вспомогательный массив
for (int step = 0; step < 8; step++) { // step - номер "цифры"
// Сортировка "подсчетом" по цифре с заданным номером
countSort(data, step, data2);
// Меняем указатели на массивы
int[] temp = data; data = data2; data2 = temp;
}
}
private static void countSort (int[] src, int nDig, int[] dest) {
int n = src.length;
// Длина массива
int[] count = new int[16];
// Массив для подсчета элементов
// 1. Подсчет
nDig <<= 2;
for (int i = 0; i < n; i++) {
count[(src[i] & (0xF << nDig)) >> nDig]++;
}
// 2. Суммирование
for (int i = 1; i < 16; i++) {
count[i] += count[i-1];
}
// 3. Расстановка
for (int i = n-1; i >= 0; i--) {
dest[--count[(src[i] & (0xF << nDig)) >> nDig]] = src[i];
}
}
© ТУИТ, кафедра СПП













 programming
programming informatics
informatics








