Similar presentations:
Алгоритм блочного шифрования Магма
1.
Алгоритм блочного шифрования МагмаШифр МАГМА относится к DES-подобным криптосистемам и представляет собой
блочный шифр, основанный на сети Фейстеля, и является доработанной версией
шифра СССР, описанного в стандарте 1989 года – ГОСТ 28147-89
Шифр МАГМА входит в стандарт Российской Федерации ГОСТ 34.12-2018 [6] как
шифр, с длинной шифруемого блока равной 64 битам. Шифр МАГМА в
стандарте 2018 года имеет ряд отличий от шифра, представленного в стандарте
1989 года, однако структура шифра и набор операций шифрования в целом
остались неизменными. Основным отличием стала фиксированная таблица
подстановки, что избавило данный шифр от потенциальных уязвимостей,
возникающих при некорректном формировании таблицы подстановки. Шифр
ориентирован на блок в 64 бита, имеет ключ размером 256 бит и 32 раунда
шифрования, что определяет его криптостойкость.
2.
Описание шифра МАГМА или чему насучит ГОСТ 34.12—2018
3.
Продолжение4.
Второе продолжение5.
Окончательное продолжение6.
Структура шифра МАГМАСтруктурная схема состоит из предварительного
разбиения 64-битного блока на два подблока по 32
бита, и и 32-х раундов шифрования, по окончании
которых полученные два блока объединяются в
выходной блок. На каждом раунде шифрования, 32
бита правого блока поступают на функцию
шифрования, вместе с 32 битами раундового ключа.
Результат функции шифрования, после сложения по
модулю 2 (операция исключающее ИЛИ) с 32
битами левого бока становится правым блоком
следующей итерации. Исходный правый блок
текущей итерации становится левым блоком
следующей итерации.
7.
Функция шифрованияНа вход функции шифрования поступает шифруемый
блок размером 32 бита, представляющий собой
правый блок сети Фейстеля и раундовый ключ
размером 32 бита. Далее, два блока складываются
друг с другом по модулю 232.
Результат сложения разбивается на 8 блоков по 4
бита, которые поступают на соответствующие блоки
подстановки S. В каждом из блоков подстановки 4
бита входных данных заменяются 4-мя битами в
соответствии с таблицами подстановки. Результаты
подстановки объединяются в 32 битный блок, после
чего к нему применяется операция циклического
сдвига влево на 11 позиций. Полученный результат
передаётся на выход функции шифрования.
8.
Генерация раундовых ключейРассмотрим генерацию раундовых ключей. Ключ в шифре Магма имеет
размер 256 бит. Для генерации раундовых ключей данный ключ
разбивается на 8 блоков по 32 бита. Обозначим их как Key1..Key8. Тогда 32
раундовых ключа K1..K32 могут быть определены в соответствии с таблицей
(следующий слайд). То есть, каждый раундовый ключ – это фрагмент
исходного ключа, выбранный по заданному алгоритму. Так первым восьми
раундовым ключам K1..K8 соответствуют ключи Key1..Key8, вторым восьми
раундовым ключам K9..K16 также соответствуют ключи Key1..Key8,
следующим восьми раундовым ключам K17..K24 снова соответствуют ключи
Key1..Key8, а вот последним восьми раундовым ключам соответствуют
ключи Key, но в обратном направлении – Key8..Key1.
9.
Определение раундовых ключейшифра Магма
Ключ(256 бит)={Key1, Key2, Key3, Key4, …,Key8}
K1
K2
K3
K4
K5
K6
K7
K8
Key1 Key2 Key3
Key4
Key5 Key6
Key7
Key8
K9
K11
K12
K13
K14
K15
K16
Key1 Key2 Key3
Key4
Key5 Key6
Key7
Key8
K17
K19
K20
K21
K22
K23
K24
Key1 Key2 Key3
Key4
Key5 Key6
Key7
Key8
K25
K28
K29
K30
K31
K32
Key8 Key7 Key6 Key5 Key4 Key3
Key2
Key1
K10
K18
K26
K27
10.
Алгоритмическая и программная реализацияшифра МАГМА – генерация ключей
12345678 12345678 12345678 87654321
11.
Модель функции генерациираундовых ключей
Не смотря на простоту алгоритма генерации раундовых ключей,
его практическая реализация выглядит достаточно неочевидно,
особенно при представлении ключей в виде массивов из ячеек.
Однако, реализаций можно придумать достаточно много.
Естественная последовательность действий может быть
представлена в следующем виде:
Разбить исходный ключ размером 256 бит на 8 блоков Key по 32
бита.
Записать побитно данные блоки в 32 ячейки, как указано в
таблице.
12.
Программная реализация генерациираундовых ключей
13.
Модель функции шифрования fФункция шифрования, в соответствии с рисунком включает в
себя три основных действия:
– Сложение двух 32 битных блоков по модулю 232.
– Подстановку.
– Циклический регистровый сдвиг влево на 11 разрядов.
Данные операции нам частично знакомы. Создадим три
функции для каждой из этих операций, а потом соберём их
вместе в виде функции шифрования.
14.
32Функция сложения по модулю 2 .
Рассмотрим операцию сложения по модулю 232. Данную
операцию можно представить в следующем виде:
r = (a + b) mod 232.
15.
Реализация сложения в десятичнойсистеме
16.
Реализация сложения для массива бит17.
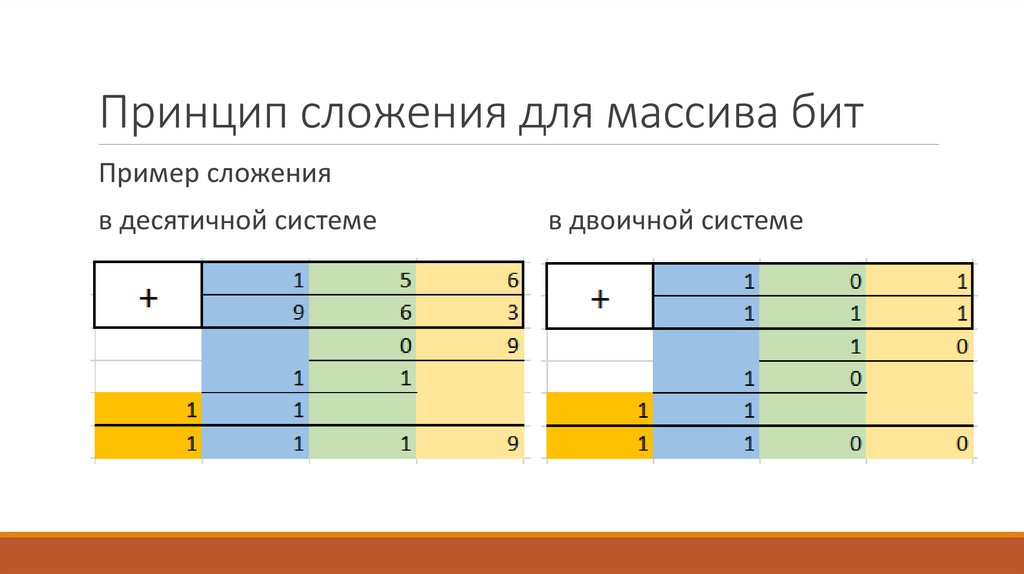
Принцип сложения для массива битПример сложения
в десятичной системе
в двоичной системе
18.
Таблица истинности с тремя входамиА032
B32
PR
C032
PRn
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
0
0
1
0
0
1
1
0
0
1
1
0
1
1
0
1
0
1
1
1
1
1
1
19.
Функция подстановки (нелинейноебиективное преобразование)
Фактически, функция подстановки замещает каждые четыре бита входного
блока на другие 4 бита, в соответствии с таблицей подстановки. Каждая
строка π соответствует S блоку. Таким образом, 4 бита поступающие на вход S
блока определяют порядковый номер ячейки в строке π, а содержимое
ячейки является подставляемым числом.
20.
Реализация функции подстановки21.
Реализация функции циклическогорегистрового сдвига на 11 позиций V1
22.
Реализация функции циклическогорегистрового сдвига на 11 позиций V2
23.
Реализация функции циклическогорегистрового сдвига на 11 позиций V3
24.
Функция шифрования25.
Моделирование шифра Магма26.
Проверка работы шифраДля проверки работы шифра Магма воспользуемся тестовыми данными из стандарта. В
стандарте указано, что для ключа:
ffeeddccbbaa99887766554433221100f0f1f2f3f4f5f6f7f8f9fafbfcfdfeff
и шифруемого блока
fedcba9876543210
результат шифрования будет:
4ee901e5c2d8ca3d

























 informatics
informatics








