Similar presentations:
Методы и алгоритмы поддержки принятия решений на основе нечеткой логики в сфере услуг страхования
1.
Методы и алгоритмыподдержки принятия решений
на основе нечеткой логики в
сфере услуг страхования
Факультет прикладной математики, информатики и механики
Есаков О. А.
Покатаев Н. В.
Воронеж 2024
2.
Предметная область и основные термины1. Страховая сумма
2. Страховая премия
3. Группы риска клиентов
4. Вероятность наступления страхового события
3.
Нечеткая логика в страховании1. Оценка рисков
2. Расчет страховых премий
3. Прогнозирование вероятности наступления страхового случая
4. Управление убытками
4.
АвтострахованиеРазмер страховой премии
Стаж
Годовой пробег
Возраст
Манера вождения
История ДТП
Категория и
стоимость ТС
5.
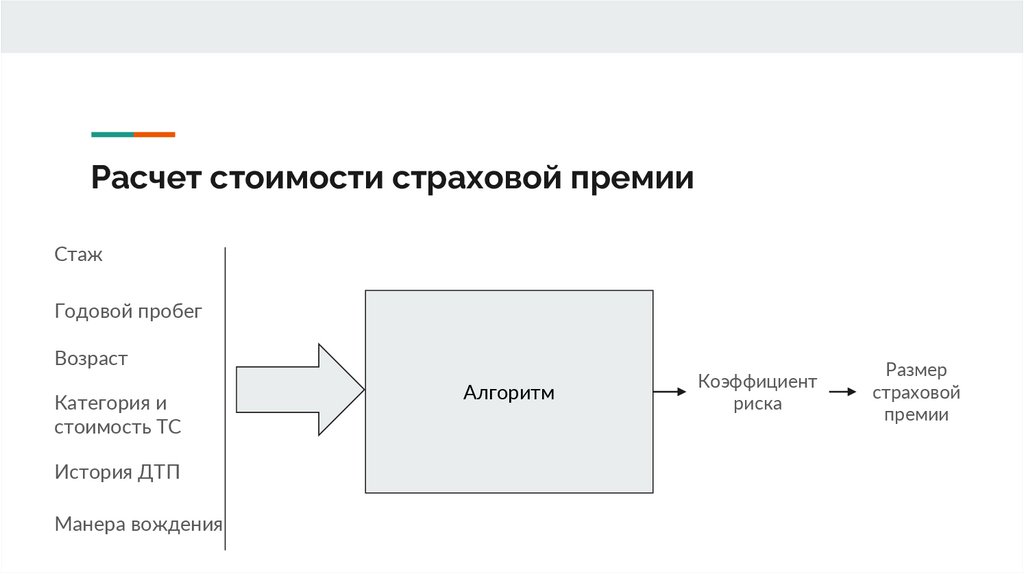
Расчет стоимости страховой премииСтаж
Годовой пробег
Возраст
Категория и
стоимость ТС
История ДТП
Манера вождения
Алгоритм
Коэффициент
риска
Размер
страховой
премии
6.
Алгоритм Мамдани1.
2.
3.
4.
5.
6.
Формирование базы правил систем нечеткого вывода
Фаззификация входных переменных
Агрегирование подусловий
Активизация подзаключений
Аккумуляция заключений
Дефаззификация выходных переменных
7.
Правила системы нечеткого вывода1. ЕСЛИ «стаж маленький» И «возраст маленький» ТО «группа высокого риска»
2. ЕСЛИ «стаж маленький» И «возраст большой» ТО «группа среднего риска»
3. ЕСЛИ «стаж большой» И «возраст большой» ТО «группа низкого риска»
8.
Зависимость риска от стажа и возрастаСтаж
Мал
Сред
Бол
Мал
Высокий
Средний
Средний
Сред
Высокий
Средний
Низкий
Бол
Средний
Средний
Низкий
9.
Зависимость риска от стажа и возрастаСтаж
1
7
15
20
0.9
0.6
0.6
40
0.9
0.6
0.4
60
0.6
0.6
0.4
10.
Агрегирование подусловийФункции принадлежности μ (y) каждого из элементарных подзаключений
консеквентов всех продукционных правил находятся при помощи одного из
методов нечеткой композиции:
min–активизация - μ(y)=min{ c; μ(x)}
prod-активизация - μ(y)=cμ(x)
average-активизация - μ(y)=0.5 (c + μ(x))
11.
Аккумуляция заключенийАлгебраическое объединение: ∀ x ∈ XμA+Bx = μAx + μBx - μAx μBx
Граничное объединение: ∀ x ∈ X μA B x = min{ μAx ⋅ μBx; 1},
Драстическое объединение ∀ x ∈ XμA∇ B (x)=
А также λ -суммы ∀ x ∈ Xμ(A+B) x = λ μAx + (1 - λ)μBx , λ∈[0;1].
,
12.
Дефаззификация выходных переменныхμi(x) — функция принадлежности соответствующего нечеткого множества Ei;
Min и Max — границы универсального множества;
yi — результат дефаззификации.












 mathematics
mathematics








