Modeli_i_modelirovanie

1. Модели и моделирование. Представление результатов моделирования

2.

Модель — упрощенное подобие реального объекта, процесса
или явления, которое отражает его существенные свойства и
характеристики.
Моделирование в информатике — это процесс создания и
работы с моделями с целью познания реальности, решения
задач или проектирования новых объектов.

3. Виды моделей

1. Логические модели описывают объекты и связи между
ними при помощи логических высказываний. Например,
логическая модель животного может быть такой:
«Животное — это существо, которое дышит, питается и
размножается».
Логические модели используются для анализа и проверки
правильности утверждений и рассуждений.

4. Виды моделей

2. Математические модели описывают объекты и процессы
при помощи математических формул и функций.
Например, математическая модель падения тела может
быть такой:
Математические модели используются для
предсказания значений различных величин.
расчета
и

5. Виды моделей

3. Графические модели описывают объекты и процессы при
помощи графиков, диаграмм, рисунков и т. д. Например,
графическая модель структуры компьютера может быть
такой:

6.

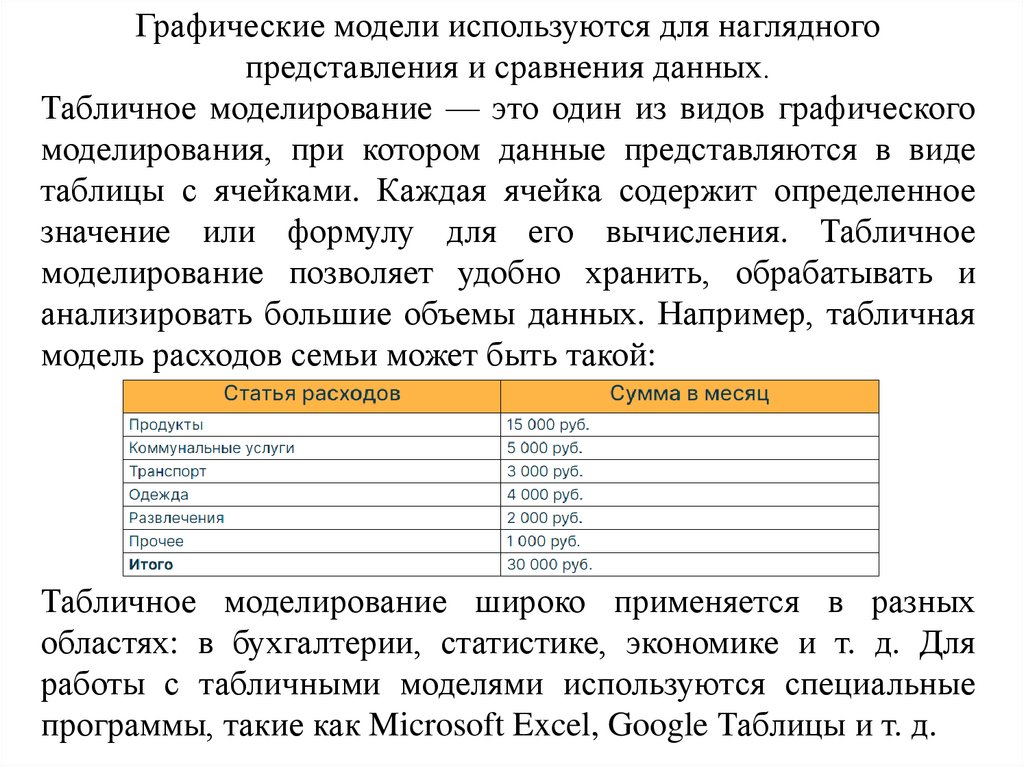
Графические модели используются для наглядного
представления и сравнения данных.
Табличное моделирование — это один из видов графического
моделирования, при котором данные представляются в виде
таблицы с ячейками. Каждая ячейка содержит определенное
значение или формулу для его вычисления. Табличное
моделирование позволяет удобно хранить, обрабатывать и
анализировать большие объемы данных. Например, табличная
модель расходов семьи может быть такой:
Табличное моделирование широко применяется в разных
областях: в бухгалтерии, статистике, экономике и т. д. Для
работы с табличными моделями используются специальные
программы, такие как Microsoft Excel, Google Таблицы и т. д.

7. Пример 1

Вот таблица расстояний между населенными пунктами:
Определи длину кратчайшего пути между пунктами А и Д.
Передвигаться можно только по дорогам, протяженность
которых указана в таблице.

8.

9.

Граф — абстрактная структура данных, которая состоит из
множества объектов, называемых вершинами или узлами, и
множества связей между ними, называемых ребрами или
дугами.
Графы используются для моделирования различных сетевых
структур, таких как дорожные сети, компьютерные сети,
социальные сети и т. д. Графы позволяют изучать свойства и
отношения объектов, а также решать разные задачи на них.

10.

В зависимости от характера связей между вершинами
различают разные виды графов. Например, граф может быть
неориентированным
или
ориентированным.
В
неориентированном графе ребра не имеют направления и
соединяют две вершины взаимно. В ориентированном графе
ребра имеют направление и соединяют две вершины
односторонне.
Например,
на
рис.
1
показан
неориентированный граф, а на рис. 2 — ориентированный.

11.

Графы также могут быть взвешенными или невзвешенными. В
взвешенном графе каждому ребру приписано некоторое
числовое значение, называемое весом или стоимостью. В
невзвешенном графе все ребра равнозначны и не имеют веса.
Например, на рис. 3 показан взвешенный граф, а на рис. 4 —
невзвешенный.

12.

Графы широко применяются в информатике. Они помогают
представлять и анализировать различные объекты и
процессы, такие как:
•структуры данных (деревья, списки, хеш-таблицы и т. д.);
•алгоритмы (поиск кратчайшего пути, поиск в ширину или
глубину, топологическая сортировка и т. д.);
•компьютерные сети (маршрутизация данных, обнаружение
циклов и тупиков, оптимизация пропускной способности и
т. д.);
•социальные сети (анализ связности и центральности узлов,
поиск сообществ и лидеров, распространение информации и
влияния и т. д.);
•дорожные сети (построение оптимальных маршрутов,
расчет пробок и заторов, планирование транспортной
инфраструктуры и т. д.).

13.

Таблица расстояний — это способ представления взвешенного
графа в виде двумерной матрицы, в которой строки и
столбцы соответствуют вершинам графа, а элементы
матрицы — весам ребер между ними. Если ребра нет, то
вместо веса ставится ноль или бесконечность.

14.

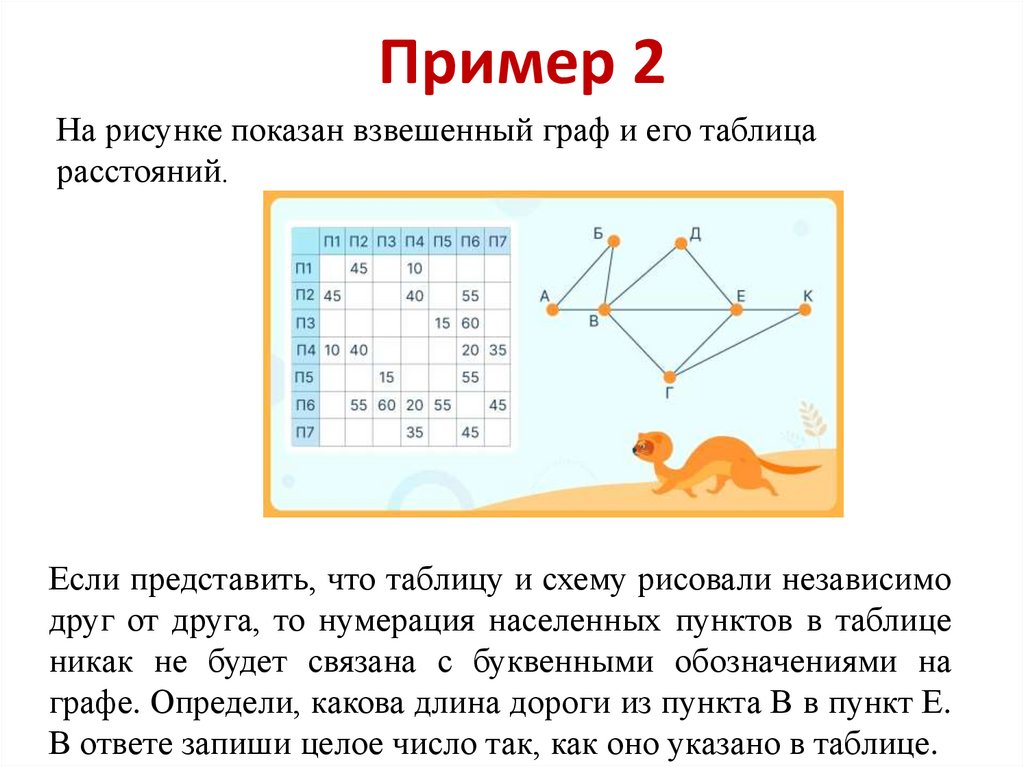
Пример 2
На рисунке показан взвешенный граф и его таблица
расстояний.
Если представить, что таблицу и схему рисовали независимо
друг от друга, то нумерация населенных пунктов в таблице
никак не будет связана с буквенными обозначениями на
графе. Определи, какова длина дороги из пункта В в пункт Е.
В ответе запиши целое число так, как оно указано в таблице.