Similar presentations:
Гипотезы прочности
1. ГИПОТЕЗЫ ПРОЧНОСТИ
2. СОДЕРЖАНИЕ
1. Назначение гипотез прочности2. Гипотезы прочности
а) гипотеза Галлилея
б) гипотеза Мариотта
в) гипотеза эквивалентного напряжения
г) гипотеза Мора
д) гипотеза энергии формоизменения.
3. Расчет бруса круглого поперечного сечения
при сочетании основных деформаций.
4. Домашнее задание.
3. Назначение гипотез прочности
Различные материалы имеют разные предельныенапряжения. Для пластичных – это Ϭт, для
хрупких – Ϭв.
Задача гипотез прочности состоит в разработке
критерия, позволяющего сравнивать разнотипные
напряженные состояния с точки зрения их
близости к предельному.
Это сравнение производится с помощью
эквивалентного напряженного состояния при
простом растяжении или сжатии.
4.
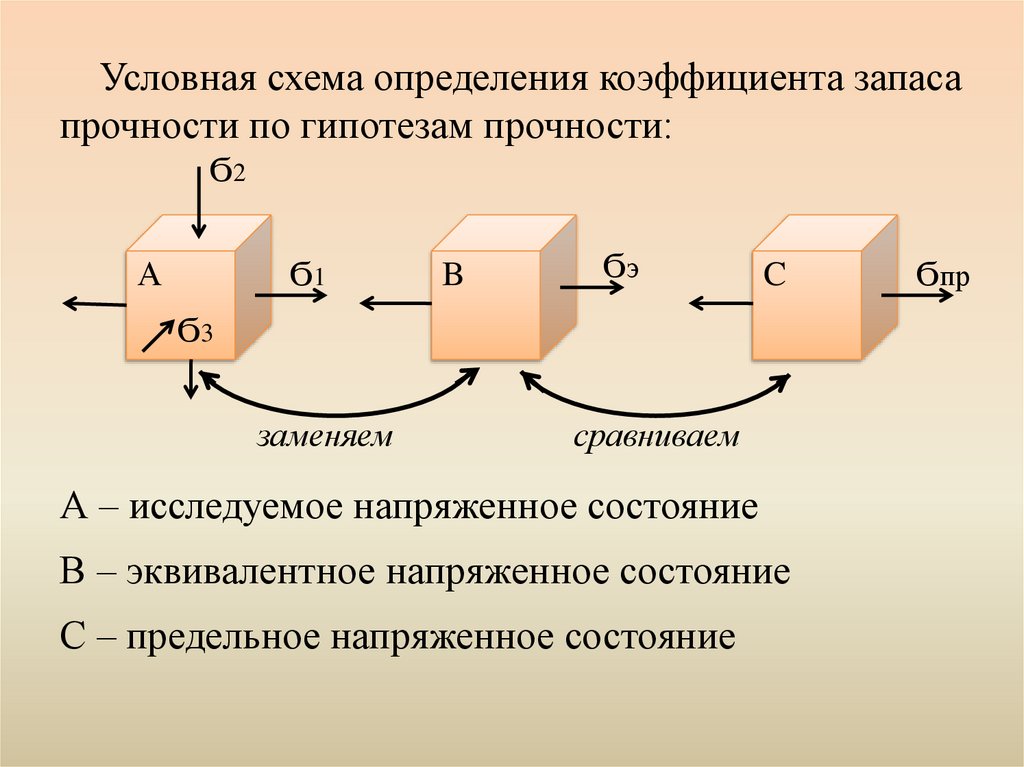
Условная схема определения коэффициента запасапрочности по гипотезам прочности:
Ϭ2
А
Ϭ1
B
Ϭэ
C
Ϭ3
заменяем
сравниваем
А – исследуемое напряженное состояние
В – эквивалентное напряженное состояние
С – предельное напряженное состояние
Ϭпр
5.
Напряжение при растяжении, равноопасноезаданному сложному напряженному состоянию,
называется эквивалентным напряжением.
Ϭэ – это условная расчетная величина, зависящая от
заданного напряженного состояния и от принятого
для расчета признака равноопасности напряженных
состояний.
Гипотезы, указывающие признаки равноопасности
различных напряженных состояний, называются
гипотезами прочности.
Условие прочности:
или
6. ГИПОТЕЗЫ ПРОЧНОСТИ
а). Гипотеза Галиллея, XVIIВ.Причиной разрушения материала является наибольшее нормальное напряжение растяжения Ϭр или
сжатия Ϭс.
Эта гипотеза справедлива только для линейного напряженного состояния.
б). Гипотеза Мариотта, 1773 г.
Прочность материала в исследуемой точке достигает критического состояния при максимальном
значении линейной деформации Ɛ.
7.
в). Гипотеза Кулона, 1773г.Предельное напряженное состояние возникает в
момент, когда наибольшие касательные
напряжения достигают предельного значения.
Гипотеза применима только для пластичных
материалов, для которых Ϭвр = Ϭвс и для
напряженных состояний, у которых Ϭ1 и Ϭ3
имеют разные знаки или одно из них равно нулю.
Эквивалентное напряжение: Ϭэ = Ϭ1 – Ϭ3
8.
г). Гипотеза Мора, 1900 г.Учитывает Ϭ и τ напряжения. Справедлива как для
пластичных, так и для хрупких материалов. Дает
наилучшие результаты, если Ϭ1 и Ϭ3 имеют разные
знаки или одно из них равно нулю.
Ϭэ = Ϭ1 – ν · Ϭ3
для хрупких:
для пластичных:
для хрупкопластичных:
9.
д). Гипотеза энергии формоизменения.Выдвинута Бельтрами В 1885 г и усовершенствована
др. учеными.
Предельное напряженное состояние возникает при
некотором значении, потенциальной энергии,
накапливаемой элементами конструкции при
изменении их формы.
Справедлива только для пластичных материалов, у
которых Ϭтр = Ϭтс
10. Расчет бруса круглого сечения при изгибе с кручением.
уМ2
М1
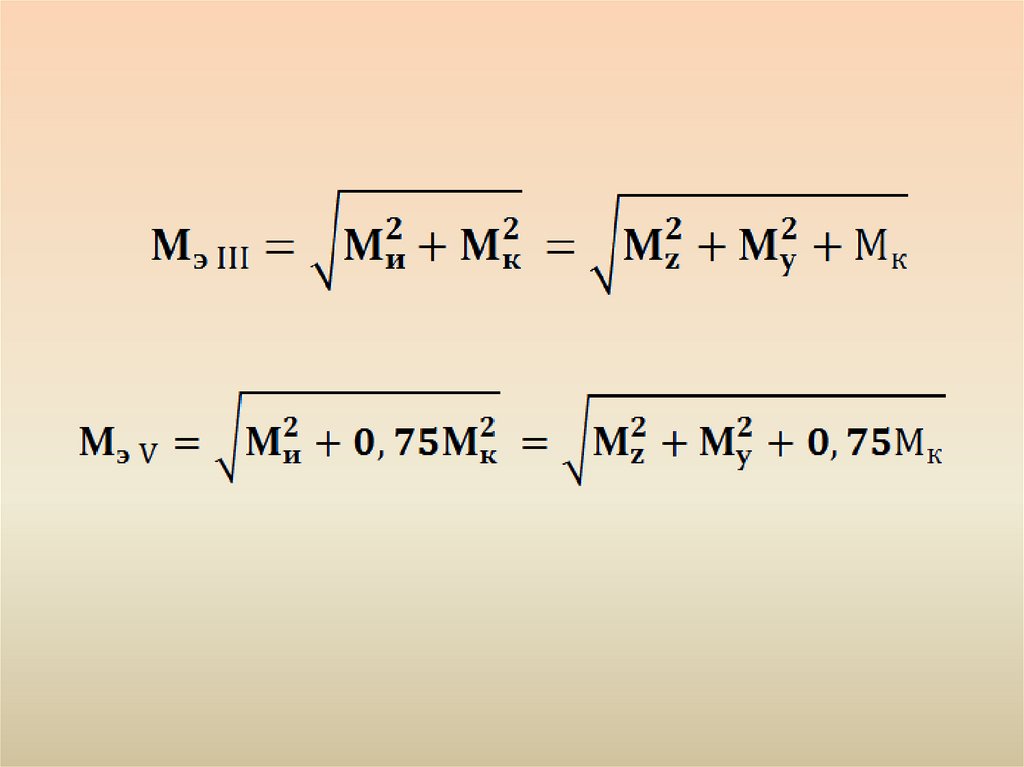
по III гипотезе прочности:
х
А
по IV гипотезе:
z
эпюра Мк
+
Напряжения изгиба:
эпюра Ми
-
Напряжения кручения:
τ
τ
Ϭ
А
11.
Момент сопротивления при изгибе:Момент сопротивления при кручении:
т.к. Wр = 2Wи =>
Т.О.: расчитывая брус при изгибе с кручением, эквивалентные напряжения можно определить сразу по крутящему и
изгибающему моментам, возникшим в опасном сечении.
12.
Причем:- эквивалентные
моменты
При пространственном нагружении бруса в его сечениях кроме крутящего момента Мк под действием
вертикальных сил возникает изгибающий момент Мz,
а под действием горизонтальных сил – изгибающий
момент Му.
=>
13.
14. ДОМАШНЕЕ ЗАДАНИЕ
А.И. Аркуша Техническая механикаСтр. 326 – 334
В.П. Олофинская Техническая механика
Стр. 278 – 283
Лекции
15.
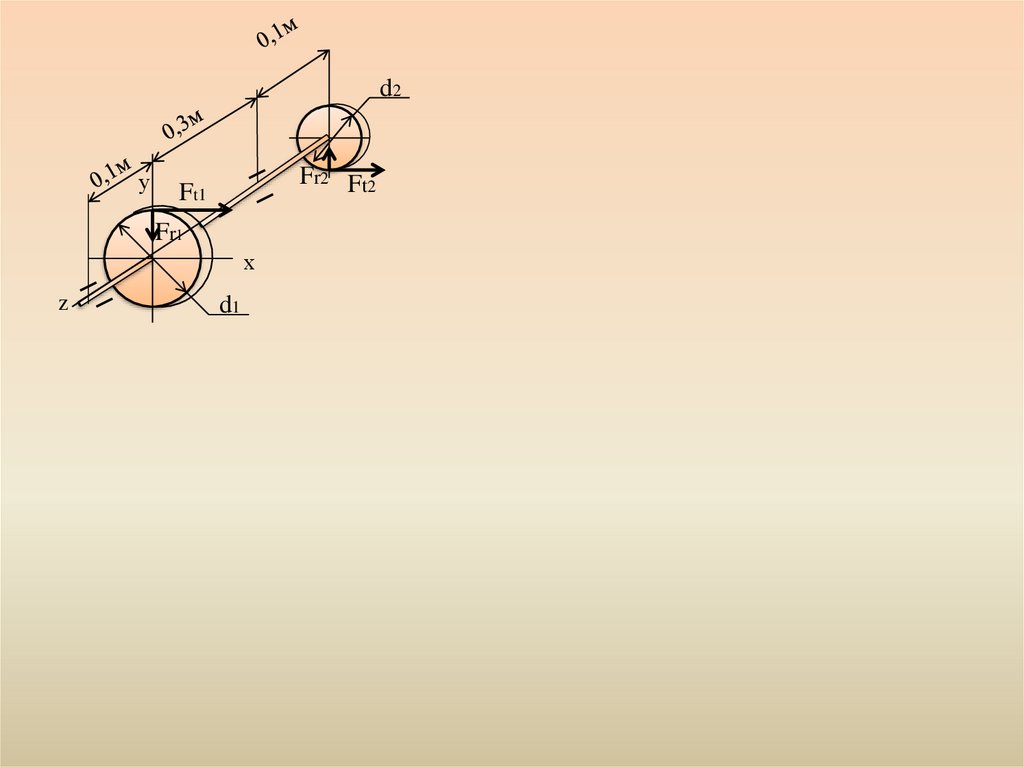
d2у
Fr2 Ft2
Ft1
Fr1
х
z
d1
16.
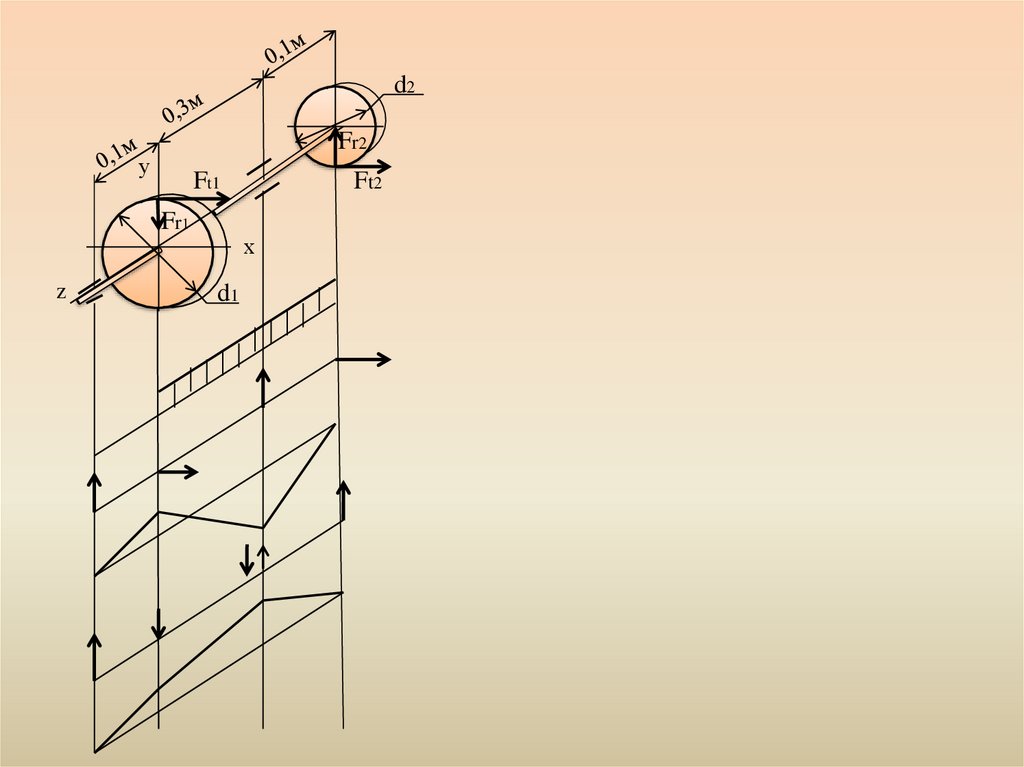
d2Fr2
у
Ft1
Fr1
z
Ft2
х
d1












 mechanics
mechanics