Similar presentations:
Линейные структуры данных (лекция 1)
1.
1Красников Степан Альбертович
Структуры и алгоритмы обработки данных
(часть 2)
Лекция 1
Москва 2022
2.
2Условия обучения
• По итогам изучения дисциплины проводится экзамен;
• В течение семестра необходимо выполнить все задания, которые выложены на Учебном
портале (ЭИОС);
• Для допуска к экзамену необходимо защитить не менее четырех практических работ;
• Оценка на экзамене ставится по пятибалльной шкале в зависимости от количества балов
полученных за практические работы (до 25 баллов) и набранных на самом экзамене (до 50
баллов).
3.
3Рекомендуемая литература
1.
Вирт Н. Алгоритмы и структуры данных. Новая версия для Оберона, 2010.
2.
Кнут Д. Искусство программирования. Тома 1-4, 1976-2013.
3.
Ахо А.В. и др. Разработка и анализ компьютерных алгоритмов, 2021.
4.
Кормен Т.Х. и др. Алгоритмы. Построение и анализ, 2013.
5.
Лафоре Р. Структуры данных и алгоритмы в Java. 2-е изд., 2013.
6.
Макконнелл Дж. Основы современных алгоритмов. Активный обучающий метод. 3-е
доп. изд., 2018.
7.
Скиена С. Алгоритмы. Руководство по разработке, 2011.
8.
Хайнеман Д. и др. Алгоритмы. Справочник с примерами на C, C++, Java и Python, 2017.
9.
Бхаргава А. Грокаем алгоритмы. Иллюстрированное пособие для программистов и
любопытствующих, 2017.
10. Гасфилд Д. Строки, деревья и последовательности в алгоритмах. Информатика и
вычислительная биология, 2003.
4.
4Темы дисциплины осеннего семестра
Тематика третьего семестра посвящена изучению нелинейных структур данных.
Материал по нелинейным структурам представлен в двух разделах: деревья и графы.
В каждом разделе рассматриваются способы построения, представления и основные
операции над нелинейными структурами: деревья, леса, которые предоставляют
возможность хранить иерархические отношения, и графами, позволяющими хранить
сетевые отношения.
В разделе Деревья рассматриваются способы представления деревьев в памяти компьютера
на массивах и связанных структурах данных и особенность представления полного и
совершенного деревьев.
Большое внимание уделяется применению деревьев в качестве структуры данных для
оптимизации поиска в других структурах данных (например, файлах или базах данных),
это так называемые поисковые деревья. Рассматриваются алгоритмы их построения,
модификации и поиска элемента данных по ключу.
5.
5Темы дисциплины осеннего семестра
В разделе Графы рассматриваются различные способы реализации структуры данных граф
в программе. Иллюстрируются и исследуются на примерах алгоритмы обхода графов,
нахождение кратчайших путей между вершинами, поиска его элементов: циклов, диаметра,
Приводятся иллюстрации алгоритмов построения остовных деревьев графа,
применяющихся в алгоритмах поиска по графу.
В разделе Стратегии разработки алгоритмов рассматриваются стратегии разработки NPполных задач по получению оптимального или подходящего решения: жадный алгоритм,
динамическое программирование, дерево решений, метод ветвей и границ.
6.
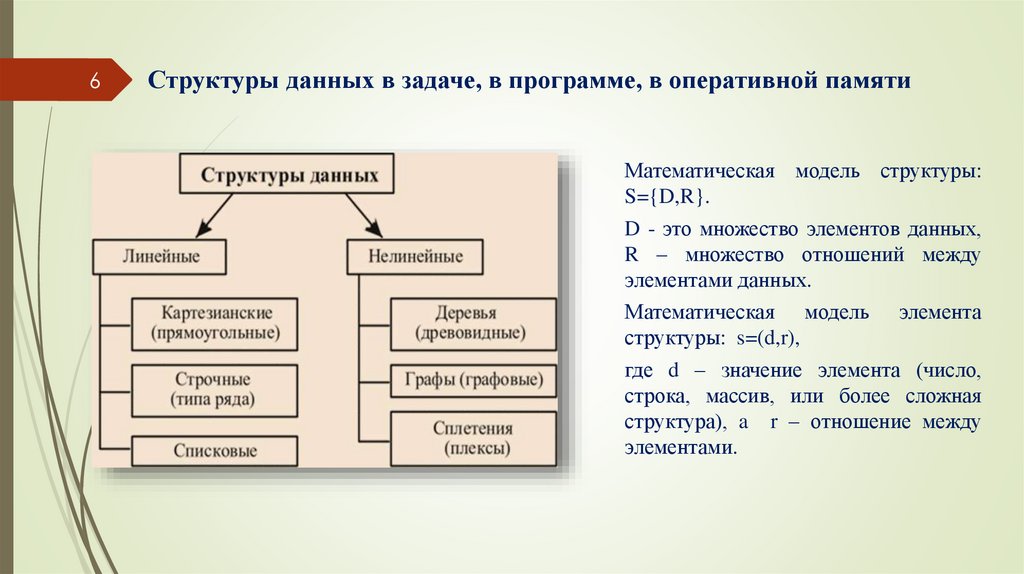
6Структуры данных в задаче, в программе, в оперативной памяти
Математическая модель структуры:
S={D,R}.
D - это множество элементов данных,
R – множество отношений между
элементами данных.
Математическая модель элемента
структуры: s=(d,r),
где d – значение элемента (число,
строка, массив, или более сложная
структура), a r – отношение между
элементами.
7.
7Линейные структуры данных
Под линейной структурой данных будем понимать множество элементов, для которых
свойственны линейные отношения между элементами, суть которых можно определить
так:
• это последовательность элементов, в которой элементы упорядочены в соответствии
с порядковым номером (a1, a2, … , ak);
• есть первый элемент с номером 1 и последний с номером k;
• у элемента с номером i (i≠1
следующий, с номером i+1.
и i≠k) есть предшествующий с номером i-1 и
В линейных структурах данных доступ к элементу реализуется через номер элемента.
В массиве этот доступ прямой по индексу. Индекс используется для определения адреса
ячейки в составе массива.
Адрес ячейки с индексом i = Адрес ячейки с номером 0 + i * L
Где, L – размер одной ячейки массива в байтах, а i * L – это смещение в байтах от
начала массива.
8.
8Нелинейные структуры данных
Нелинейная структура данных - это структура данных, в которой элемент данных связан
отношением (или можно сказать, что имеет доступ) с несколькими другими элементами
структуры данных и связи между элементами зависят от выполнения определенного
условия.
В зависимости от поддерживаемых связей между элементами нелинейные структуры
данных можно разделить на три класса:
- иерархические (древовидные);
- сетевые (или по другому графовые);
- сплетения (плексы).
9.
9Нелинейные структуры данных (примеры)
Пример 1. Иерархические отношения/отношения подчинения.
Дерево папок
ОС Windows
Оглавление книги
Организационная диаграмма,
представляющая структуру
административного
звена
организации
10.
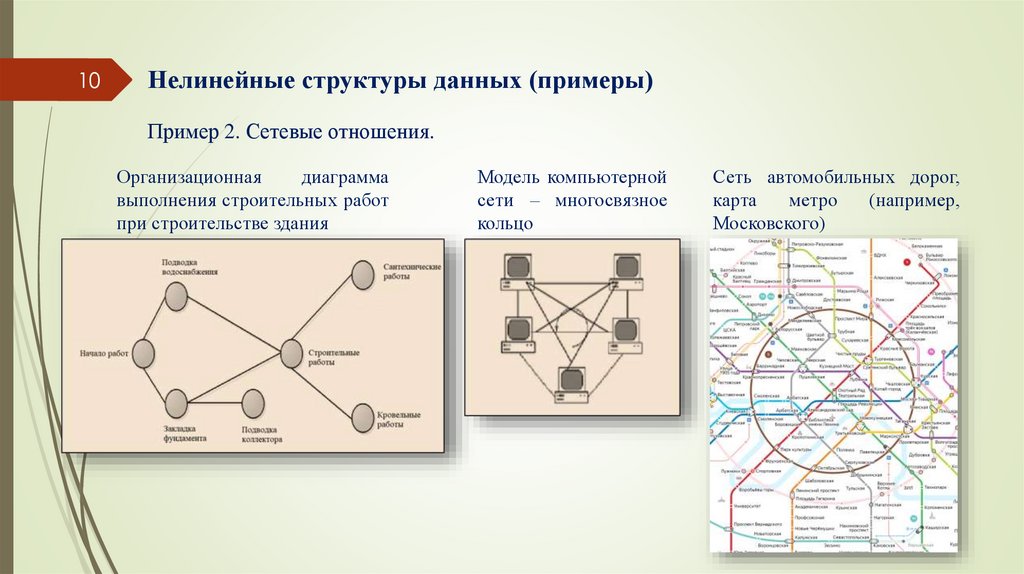
10Нелинейные структуры данных (примеры)
Пример 2. Сетевые отношения.
Организационная
диаграмма
выполнения строительных работ
при строительстве здания
Модель компьютерной
сети – многосвязное
кольцо
Сеть автомобильных дорог,
карта
метро
(например,
Московского)
11.
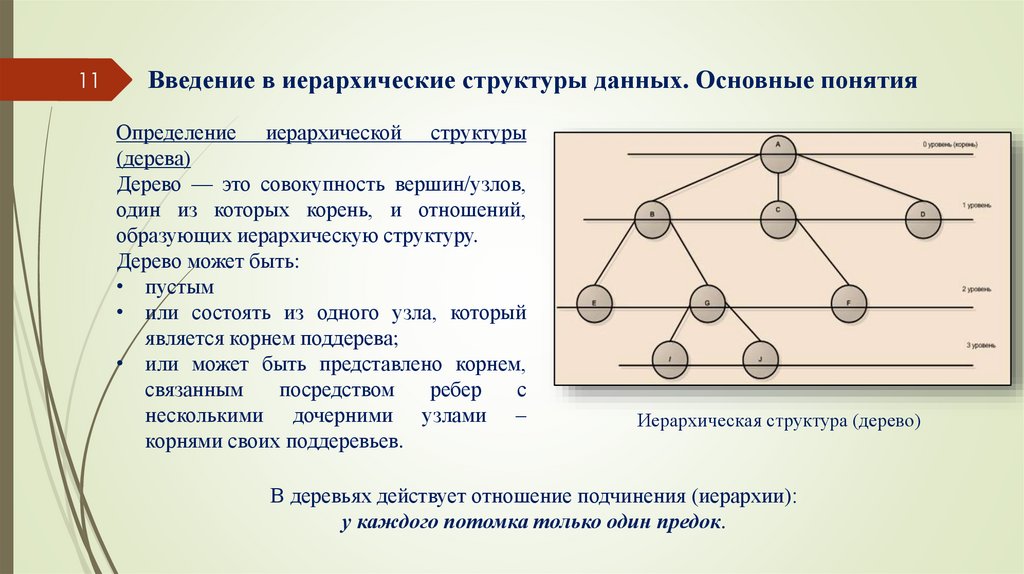
11Введение в иерархические структуры данных. Основные понятия
Определение иерархической структуры
(дерева)
Дерево — это совокупность вершин/узлов,
один из которых корень, и отношений,
образующих иерархическую структуру.
Дерево может быть:
• пустым
• или состоять из одного узла, который
является корнем поддерева;
• или может быть представлено корнем,
связанным
посредством
ребер
с
несколькими дочерними узлами –
корнями своих поддеревьев.
Иерархическая структура (дерево)
В деревьях действует отношение подчинения (иерархии):
у каждого потомка только один предок.
12.
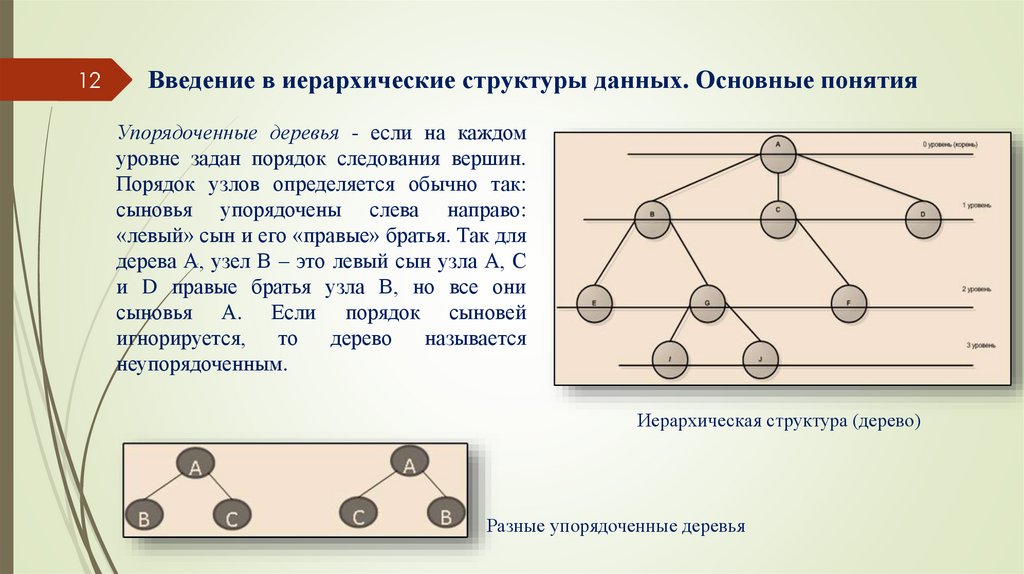
12Введение в иерархические структуры данных. Основные понятия
Упорядоченные деревья - если на каждом
уровне задан порядок следования вершин.
Порядок узлов определяется обычно так:
сыновья упорядочены слева направо:
«левый» сын и его «правые» братья. Так для
дерева А, узел В – это левый сын узла А, С
и D правые братья узла В, но все они
сыновья А. Если порядок сыновей
игнорируется,
то
дерево
называется
неупорядоченным.
Иерархическая структура (дерево)
Разные упорядоченные деревья
13.
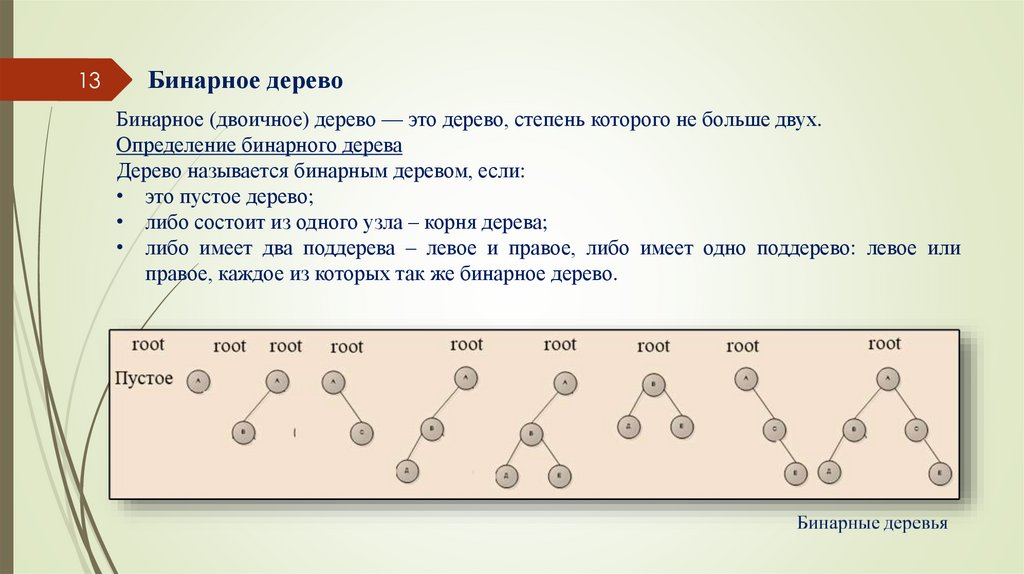
13Бинарное дерево
Бинарное (двоичное) дерево — это дерево, степень которого не больше двух.
Определение бинарного дерева
Дерево называется бинарным деревом, если:
• это пустое дерево;
• либо состоит из одного узла – корня дерева;
• либо имеет два поддерева – левое и правое, либо имеет одно поддерево: левое или
правое, каждое из которых так же бинарное дерево.
14.
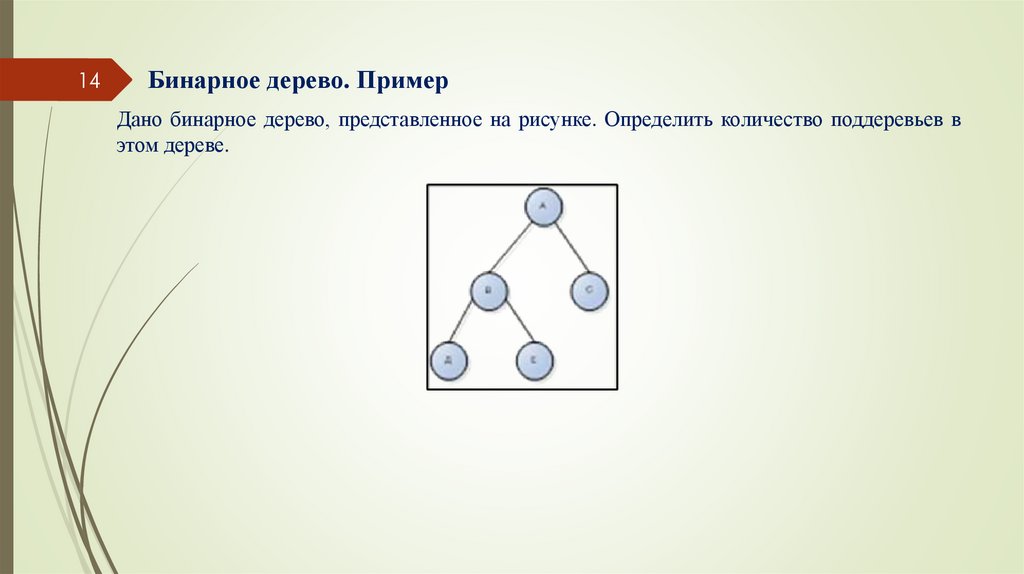
14Бинарное дерево. Пример
Дано бинарное дерево, представленное на рисунке. Определить количество поддеревьев в
этом дереве.
15.
15Абстрактный тип данных бинарное дерево
Абстрактный тип данным (далее АТД) определяет данные и операции (действия) над ними,
без указания способа реализации данных.
Определим базовый набор операций над бинарным деревом, которые будем далее
использовать.
АТД BinTree {
Данные
Список узлов дерева
N - количество узлов в дереве
Root - корень дерева
TNode – тип узла дерева
Tdata – тип информационной части узла дерева
Операции
//Создание бинарного дерева
CreateBinTree (BinTree T);
//Возвращает левое поддерево дерева Т
LeftTree(BinTree T)
//Возвращает правое поддерево дерева Т
RightTree(BinTree T)
16.
16Абстрактный тип данных бинарное дерево
//Создание узла бинарного дерева
CreateNode(Tdata d)
//Возвращает количество листьев
Leaves(T);
//Возвращает номер уровня узла n
Level(n);
//Возвращает количество узлов в дереве Т
CountNodes(T);
//Возвращает высоту дерева Т
heightTree(T);
//Обход дерева Т в прямом порядке: вывод списка
меток узлов
PreOrderTree(T);
// Обход дерева Т в обратном порядке: вывод
списка меток узлов
PostOrderTree(T);
// Обход дерева Т в симметричном порядке:
вывод списка меток узлов
InOrderTree(T);
//Вывод дерева на монитор
PrintTree(T);
//Определение дерева на пусто. Результат: true –
пустое, иначе false
Empty(T);
//Нахождение родителя узла n. Возвращает узел.
Parent(n);
//Возвращает корень дерева Т
Root(T);
//Возвращает значение информационной части
узла n
Data(n);
}
17.
17Алгоритмы определения параметров бинарного дерева
1. Количество листьев в дереве
Лист – это узел, у которого нет поддеревьев.
Рекуррентное определение количества листьев в бинарном дереве
0 если дерево Т пусто
Leaves (T ) 1 если дерево Т лист
Leaves ( LeftTree (T )) Leaves ( RightTree(T )) иначе
2. Высота дерева
Высота дерева — это количество ребер между корневым узлом и наиболее удаленным
листом или максимальный уровень.
1 если Т пусто
Hight (T )
1 max( Hight ( LeftTree(T )), Hight ( RightTree (T ))) иначе
18.
18Алгоритмы определения параметров бинарного дерева
3. Уровень узла
Уровень, на котором находится узел, можно рассчитать рекурсивно:
0 если n корень
level (n )
1 level ( Parent (n )) иначе
4. Определение количества узлов в бинарном дереве.
Количество узлов бинарного дерева Т можно определить рекурсивно:
0 если дерево Т пусто
CountNodes(T)
1 CountNodes(LeftTree(T)) CountNodes(RightTree (T)) иначе
19.
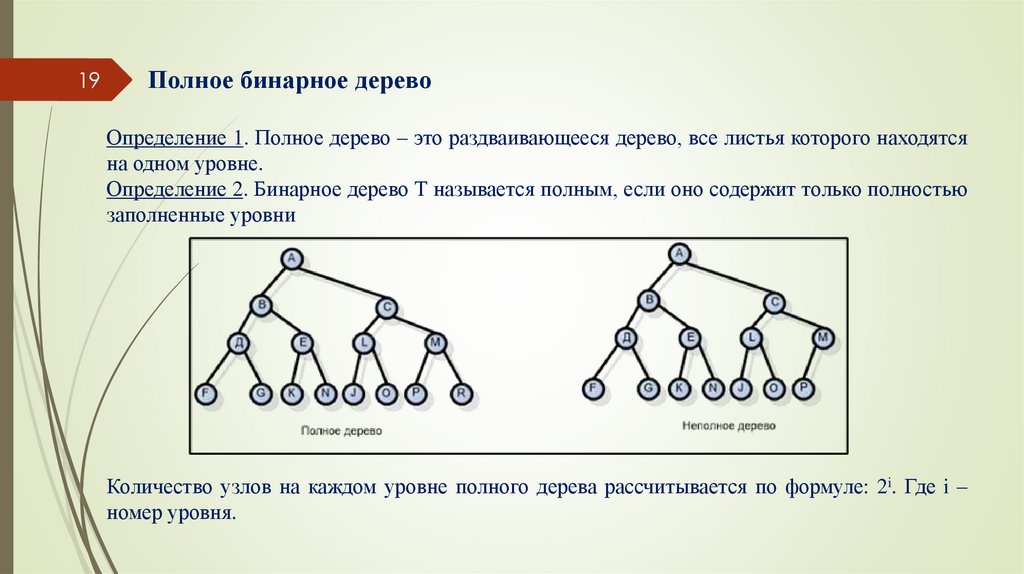
19Полное бинарное дерево
Определение 1. Полное дерево – это раздваивающееся дерево, все листья которого находятся
на одном уровне.
Определение 2. Бинарное дерево Т называется полным, если оно содержит только полностью
заполненные уровни
Количество узлов на каждом уровне полного дерева рассчитывается по формуле: 2i. Где i –
номер уровня.
20.
20Полное бинарное дерево. Примеры
Пример.
Определение высоты полного бинарного дерева по количеству узлов в дереве. Пусть, полное
бинарное дерево имеет 15 узлов. Какова высота такого дерева?
Пример.
Определение количества узлов полного бинарного дерева по его высоте.
Пусть дерево имеет высоту 4. Какое количество узлов содержит такое дерево?
Сумма членов геометрической прогрессии вычисляется по формуле
n
1
q
S b 1
q
n
1
21.
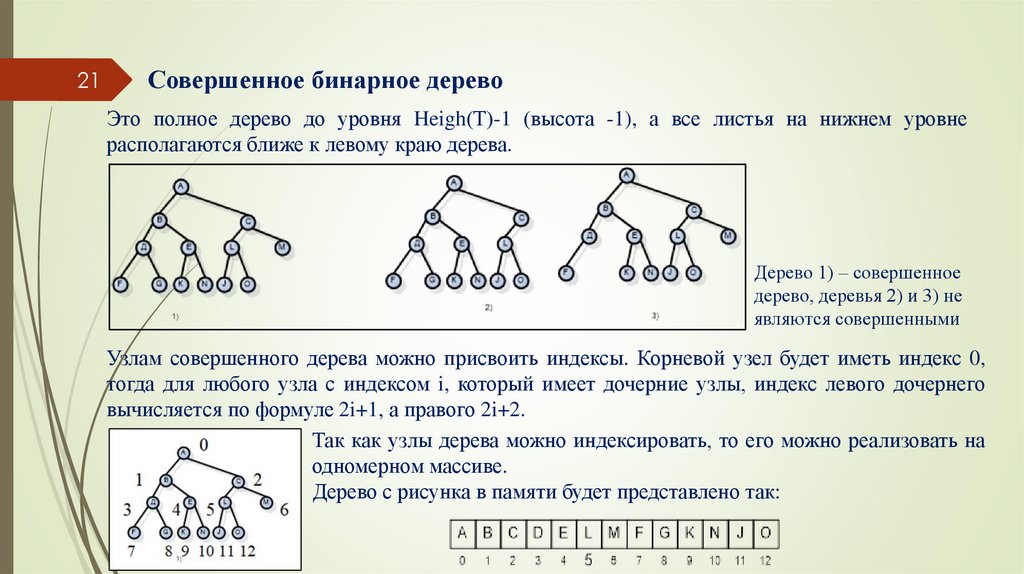
21Совершенное бинарное дерево
Это полное дерево до уровня Heigh(Т)-1 (высота -1), а все листья на нижнем уровне
располагаются ближе к левому краю дерева.
Дерево 1) – совершенное
дерево, деревья 2) и 3) не
являются совершенными
Узлам совершенного дерева можно присвоить индексы. Корневой узел будет иметь индекс 0,
тогда для любого узла с индексом i, который имеет дочерние узлы, индекс левого дочернего
вычисляется по формуле 2i+1, а правого 2i+2.
Так как узлы дерева можно индексировать, то его можно реализовать на
одномерном массиве.
Дерево с рисунка в памяти будет представлено так:
22.
Реализации бинарного дерева. В векторной памяти22
1.
В формате таблицы
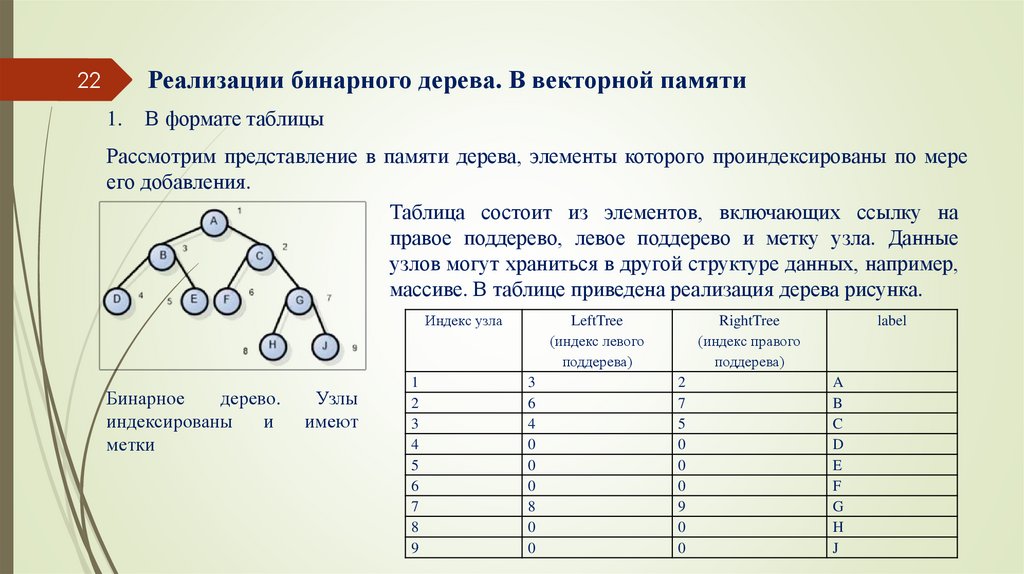
Рассмотрим представление в памяти дерева, элементы которого проиндексированы по мере
его добавления.
Таблица состоит из элементов, включающих ссылку на
правое поддерево, левое поддерево и метку узла. Данные
узлов могут храниться в другой структуре данных, например,
массиве. В таблице приведена реализация дерева рисунка.
Индекс узла
Бинарное
дерево.
индексированы
и
метки
Узлы
имеют
1
2
3
4
5
6
7
8
9
LeftTree
(индекс левого
поддерева)
3
6
4
0
0
0
8
0
0
RightTree
(индекс правого
поддерева)
2
7
5
0
0
0
9
0
0
label
A
B
C
D
E
F
G
H
J
23.
Реализации бинарного дерева. В векторной памяти23
1.
В формате таблицы
Определение реализации дерева в программе может быть таким:
struct Tnode{
int LeftTree;
int rightTree;
Tdata Label;
};
Где идентификатор Tdata определяет тип информационной части (данных) узлов
дерева.
struct BinTree{
Tnode *Table; //реализация таблицы на массиве
int Root; //индекс корня
int N;
//количество узлов
};
24.
Реализации бинарного дерева. В векторной памяти24
2.
Массив родителей
Бинарное дерево можно представит в памяти через массив родителей. Для данной реализации
узлы должны иметь числовые метки, представляющие индексы элементов массива. Тогда в
массиве каждый узел будет сохранен по индексу равному его метке. Размер массива должен
быть равен количеству узлов дерева.
Значением элемента массива родителей является метка (это индекс элемента массива) узла,
который является родителем узла с меткой индекса элемента массива. При сохранении дерева в
массиве вводится метка узла и метка родителя, заполняется соответствующий элемент массива.
Массив родителей дерева с рисунка
Бинарное дерево
представляющими
с метками,
индексы
в
0
1
1
3
3
2
2
7
7
Индексы родителей
1
2
3
4
5
6
7
8
9
Индексы массива Метки узлов
25.
Реализации бинарного дерева. В векторной памяти25
2.
Массив родителей
Программная реализация дерева на массиве родителей:
Подход 1. Данные сохраняются в отдельном массиве datas, а отношения в массиве родителей parents, но
вся информация по дереву в одной структуре типа BinTreeArrayParents.
struct BinTreeArrayParents{
int *parents;
TData *datas;
int N;
//количество узлов
};
BinTreeArrayParents bintree;
Подход 2. Элемент массива родителей хранит и данные, и метку родителя узла.
struct Tnode{
int labelParent
Tdata data;
};
struct BinTreeArrayParents{
Tnode *parents;
int N;
//количество узлов
};
BinTreeArrayParents bintree;
26.
Реализации бинарного дерева. В векторной памяти26
3.
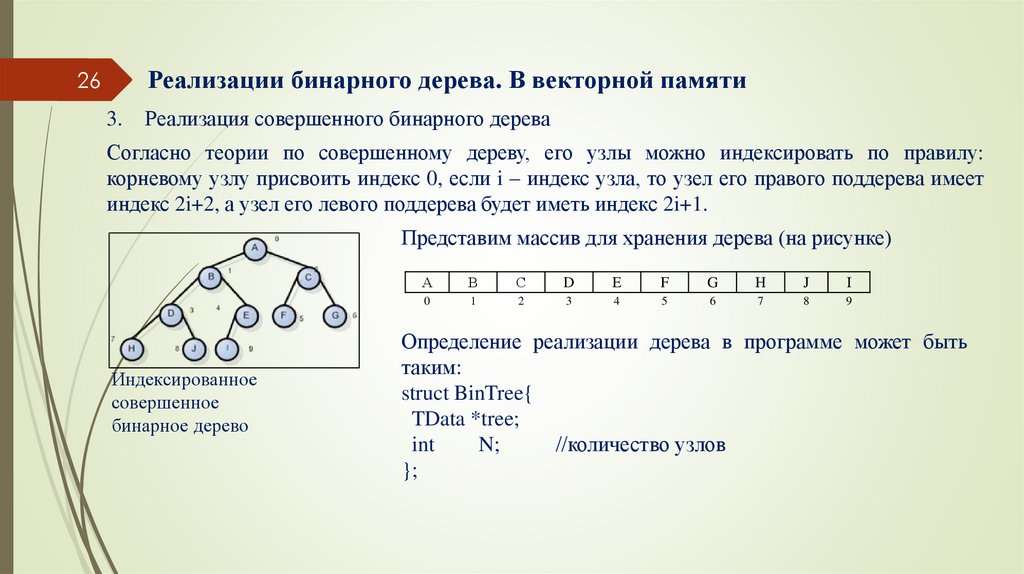
Реализация совершенного бинарного дерева
Согласно теории по совершенному дереву, его узлы можно индексировать по правилу:
корневому узлу присвоить индекс 0, если i – индекс узла, то узел его правого поддерева имеет
индекс 2i+2, а узел его левого поддерева будет иметь индекс 2i+1.
Представим массив для хранения дерева (на рисунке)
Индексированное
совершенное
бинарное дерево
А
В
С
D
E
F
G
H
J
I
0
1
2
3
4
5
6
7
8
9
Определение реализации дерева в программе может быть
таким:
struct BinTree{
TData *tree;
int
N;
//количество узлов
};
















 programming
programming








