Лекция (СиАОД ч.2) 2

1.

1
Структуры и алгоритмы обработки данных
(часть 2)
Лекция 2
Москва 2023

2.

2
Реализации бинарного дерева на связанной структуре
Структура узла бинарного дерева, реализуемого на связанной структуре, имеет вид:
Область данных
Ссылка на левое поддерево Ссылка на правое поддерево
Рассмотрим пример представления бинарного дерева на связанной структуре.
Бинарное дерево
Структура
бинарного дерева,
связанное хранение

3.

3
Алгоритмы обхода бинарного дерева
Обход дерева – это алгоритм, который позволяет осуществить доступ ко всем узлам
дерева, только один раз. Над данными посещенного узла можно выполнять операции.
Обход формирует список пройденных узлов.
Обход дерева возможен, если дерево упорядочено. Так как дерево является частным
случаем графа, то можно использовать два метода обходов, допустимых над графами:
обход в глубину — это посещение узлов по поддеревьям (по ветвям);
обход в ширину — это обход по уровням (обход сыновей).

4.

4
Алгоритмы обхода бинарного дерева
Алгоритмы обхода методом в “глубину”
1. Обход бинарного дерева в прямом порядке (префиксная форма)
посетить корневой узел;
обойти в прямом порядке левое поддерево;
обойти в прямом порядке правое поддерево.
void Pereorder (BinTree T, void Visit) {
if (! Empty(T)){
Visit(Root(T));
Pereorder(LeftTree(T),visit);
Pereorder(RightTree(T),visit);
}
}
Результат прямого обхода: F, B, A, D, C, E, G, I, H.

5.

5
Алгоритмы обхода бинарного дерева
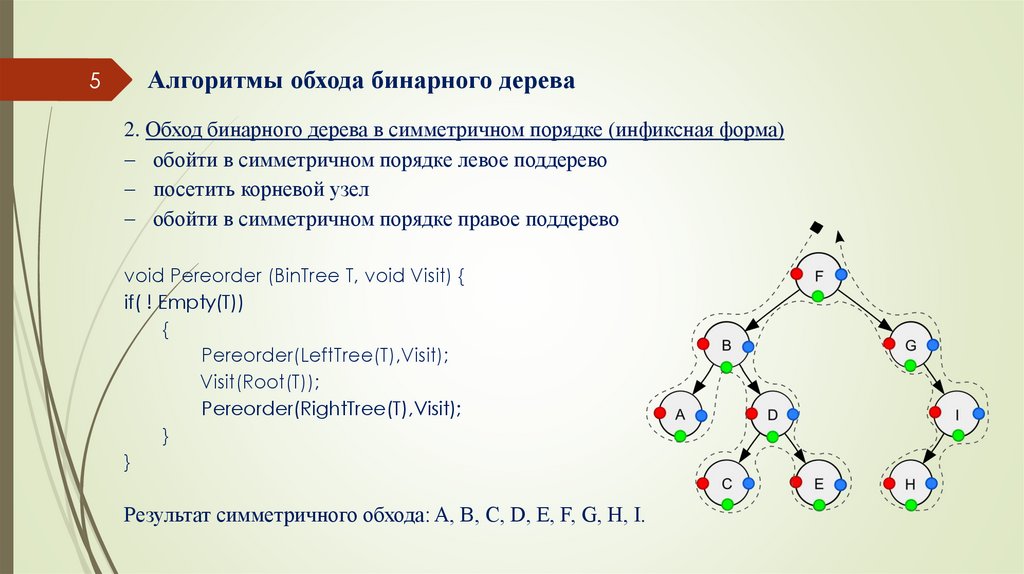
2. Обход бинарного дерева в симметричном порядке (инфиксная форма)
обойти в симметричном порядке левое поддерево
посетить корневой узел
обойти в симметричном порядке правое поддерево
void Pereorder (BinTree T, void Visit) {
if( ! Empty(T))
{
Pereorder(LeftTree(T),Visit);
Visit(Root(T));
Pereorder(RightTree(T),Visit);
}
}
Результат симметричного обхода: A, B, C, D, E, F, G, H, I.

6.

6
Алгоритмы обхода бинарного дерева
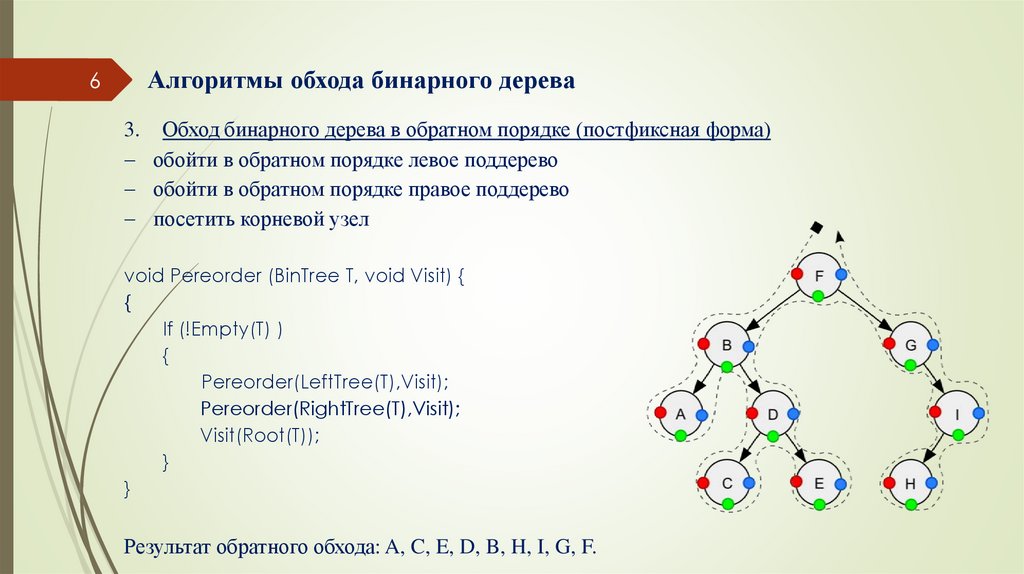
3. Обход бинарного дерева в обратном порядке (постфиксная форма)
обойти в обратном порядке левое поддерево
обойти в обратном порядке правое поддерево
посетить корневой узел
void Pereorder (BinTree T, void Visit) {
{
If (!Empty(T) )
{
Pereorder(LeftTree(T),Visit);
Pereorder(RightTree(T),Visit);
Visit(Root(T));
}
}
Результат обратного обхода: A, C, E, D, B, H, I, G, F.

7.

7
Применение алгоритмов обхода в глубину
Пример. Дано дерево выражения. Сформировать,
используя соответствующий алгоритм обхода
методом «в глубину», представление выражения:
• в постфиксной форме;
Постфиксная запись (знак операции следует за
операндами) выражения a+b/с имеет вид abc/+
• в префиксной форме;
Префиксная запись (знак операции указывается
перед операндами) выражения a+b/с имеет вид
+a/bc
• в инфиксной форме.
Дерево выражения

8.

8
Применение алгоритмов обхода в глубину
Обход дерева выражения в обратном порядке
позволяет
создать
постфиксную
запись
выражения.
ab+cde/-*
Обход дерева выражения в прямом порядке
позволяет
создать
префиксную
запись
выражения.
*+ab-c/de
Обход дерева выражения в симметричном
порядке позволяет создать инфиксную запись
выражения.
(a+b)*(c-d/e)
Дерево выражения

9.

9
Применение алгоритмов обхода в глубину
Пример. Использование алгоритма обхода для
отображения бинарного дерева на экране.
Так как узлов в дереве может быть много, то
при выводе на экран выводить информацию
надо построчно, поэтому удобно дерево
представить в перевернутом виде, как
представлено на рисунке (вид 2).
Из рисунка видно, что самым первым
выводится правый узел правого поддерева,
затем его корень, затем его левый узел и т. д.,
т.е. выводится правое дерево, затем левое
поддерево, опять с самого правого. Из
представления дерева видно, что для вывода
удобно использовать симметричный обход,
только начинать надо с правого поддерева.
Дерево выражения (1) и вид при выводе на
экран (2)

10.

10
Применение алгоритмов обхода в глубину
Реализация алгоритма вывода бинарного дерева на экран в повернутом виде
// level – номер уровня, выводимого узла.
// L - количество пробелов от уровня 0 до уровня узла по формуле level * L
void printBinTree(BinTree T.int level,int L){
int i;
If (! Empty(T))
{
printBinTree((rightTree(T), level+1, L);
for (i=1;i<=level*L; i++ ){
cout<<' ';
}
cout<<Data(T);
printBinTree((LeftTree(T), level+1, L);
}
}

11.

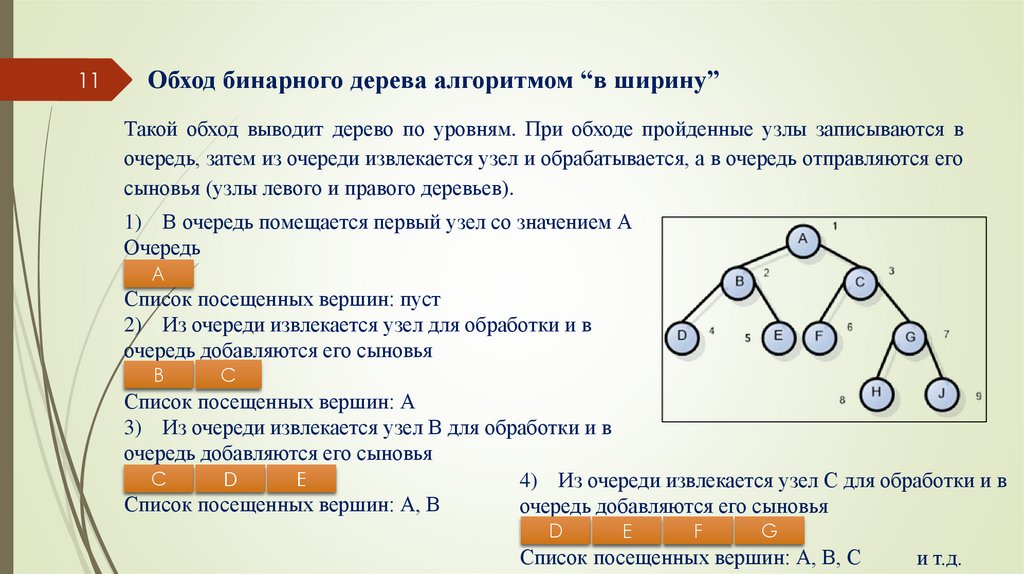
11
Обход бинарного дерева алгоритмом “в ширину”
Такой обход выводит дерево по уровням. При обходе пройденные узлы записываются в
очередь, затем из очереди извлекается узел и обрабатывается, а в очередь отправляются его
сыновья (узлы левого и правого деревьев).
1) В очередь помещается первый узел со значением А
Очередь
A
Список посещенных вершин: пуст
2) Из очереди извлекается узел для обработки и в
очередь добавляются его сыновья
B
C
Список посещенных вершин: А
3) Из очереди извлекается узел В для обработки и в
очередь добавляются его сыновья
C
D
E
4) Из очереди извлекается узел C для обработки и в
Список посещенных вершин: А, В
очередь добавляются его сыновья
D
E
F
G
Список посещенных вершин: А, В, С
и т.д.

12.

12
Обход бинарного дерева алгоритмом “в ширину”
Псевдокод алгоритма обхода бинарного дерева методом в ширину.
Используется контейнеры: vector – для формирования списка посещенных вершин, quell – очередь, для хранения
списка пока не посещенных вершин. Функции АТД BinTree для доступа к узлам дерева T.
vector<Tnode> bfs(BinTree T)
//в ширину
{
quel Q;
Tnode w;
Q.pushback(Root(Т));
vector<Tnode> listNodes;
while (Q.Empty())
{
w=Q.pop();
listNodes.pushback(w);
Tnode lefttree= LeftTree(w);
if(!Empty(lefttree)) Q.pushback(lefttree);
Tnode righttree=RightTree(w);
if(!Empty(righttree)) Q.pushback(righttree);
}
return listNodes
}

13.

13
Идеально сбалансированное бинарное дерево
Бинарное дерево называется идеально сбалансированным, если для каждой его вершины
количество вершин в левом и правом поддереве различаются не более чем на 1 и каждое его
поддерево так же идеально сбалансированное бинарное дерево.
Примеры идеально сбалансированных бинарных
деревьев
Пусть требуется построить бинарное
дерево с n узлами и минимальной высотой
(максимально "ветвистое" и "низкое").
Алгоритм
построения
идеально
сбалансированного дерева при известном
числе
вершин
n
лучше
всего
формулируется с помощью рекурсии.
Алгоритм строит дерево, применяя принцип нисходящего обхода методом «в глубину».
Описание алгоритма
взять одну вершину в качестве корня;
построить левое поддерево с nl = n DIV 2 вершинами этим же алгоритмом;
построить правое поддерево с nr = n-nl-1 вершинами этим же алгоритмом.

14.

14
Идеально сбалансированное бинарное дерево
Реализация алгоритма создания бинарного идеально сбалансированного дерева на связанной
структуре
class BinIBT
{
private:
struct Node
{
int data;
Node *left;
Node *right;
};
typedef Node *Tree;
Tree Root;
int n;
public:
BinIBT(int n1);
void createtree(Tree &T,int n);
void out(Tree &T,int i);
void print();
const static int l=5;
};
BinIBT:: BinIBT (int n1)
{
n=n1;
Root=0;
createtree(Root,n);
}
void BinIBT::createtree(Tree &T,int n)
{int nl,nr,x;
if (n!=0)
{
T=new Node;
T->left=0;
T->right=0;
cin>>x;
T->data=x;
nl=n/2;
nr=n-nl-1;
BinIBT::createtree(T->left,nl);
BinIBT::createtree(T->right,nr);
}}

15.

15
Дерево выражения
Выражение, содержащее бинарные операции, можно представить как бинарное дерево, в
котором внутренние узлы будут хранить операции, а листья операнды.
Например, выражение (a+b)*(c-d/e) можно представить деревом, в корневом узле которого
будет находиться операция *, правое поддерево будет представлять правый операнд (правая
скобка - тоже выражение), а левое поддерево – левый операнд (левая скобка - тоже
выражение).
Если операнды – числа, то дерево можно
использовать
для
вычисления
значения
выражения.
Если операнды - переменные, то в узел
операнда записывается ссылка на ячейки
переменных.
Дерево выражений можно использовать при
вычислении значения выражения. При этом
необходимо учитывать приоритетность операций
и правило: сначала надо вычислить значение
выражения левого поддерева, затем правого, а
Дерево выражения (a+b)*(c-d/e)
затем выполнить операцию, находящуюся в корне.

16.

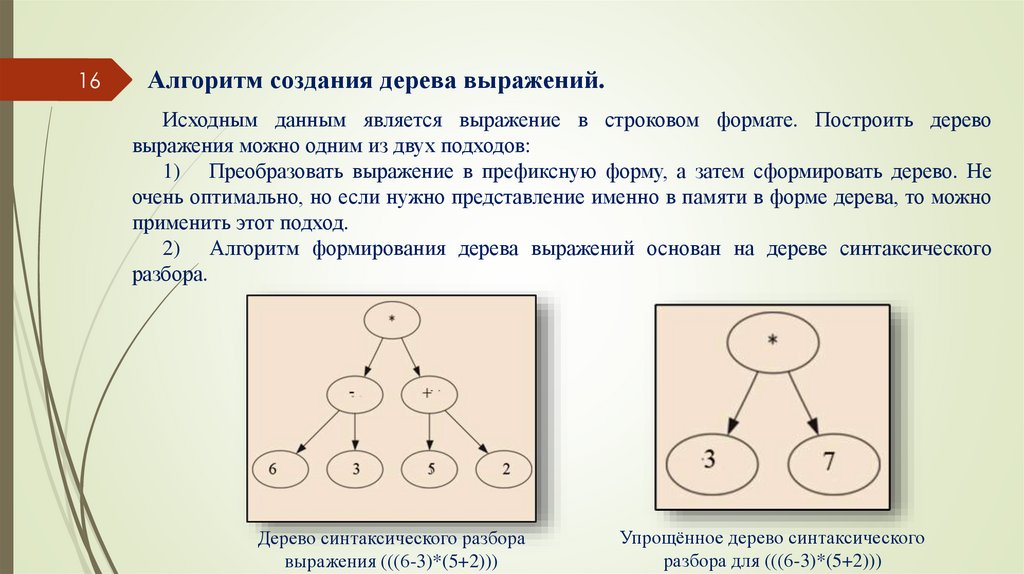
16
Алгоритм создания дерева выражений.
Исходным данным является выражение в строковом формате. Построить дерево
выражения можно одним из двух подходов:
1) Преобразовать выражение в префиксную форму, а затем сформировать дерево. Не
очень оптимально, но если нужно представление именно в памяти в форме дерева, то можно
применить этот подход.
2) Алгоритм формирования дерева выражений основан на дереве синтаксического
разбора.
Дерево синтаксического разбора
выражения (((6-3)*(5+2)))
Упрощённое дерево синтаксического
разбора для (((6-3)*(5+2)))

17.

17
Алгоритм создания дерева выражений.
Выражение со скобками можно описать рекурсивной зависимостью. Представим эту
зависимость по нотации Бэкуса-Наура, считая операндами цифры (однозначные числа):
Формула ::= цифра|(Формула операция Формула)
В указанной нотации символ ::= заменяет фразу-«по определению есть», а символ | заменяет фразу «или».
Т.е. всю запись читаем так: Формула по определению есть цифра или (Формула операция
Формула).
Выражения (6 / (4-2)) или (((6-3)*(5+2))) удовлетворяют приведенному определению.
Выражения могут не содержать скобок, тогда при формировании дерева надо учитывать
приоритет операций.

18.

18
Алгоритм создания дерева выражений.
Рассмотрим алгоритм построения дерева разбора для математического выражения с
полной расстановкой скобок.
Исходное выражение поступает как строка (6 / (4-2)) или (((6-3)*(5+2))). Оно записано
верно, в соответствии с определением, баланс скобок выполнен.
В выражении несколько видов символов, которые указывают на действие, которое должен
выполнить алгоритм, когда при разборе выражения он встретился.
Левая скобка - означает начало нового выражения и, следовательно, необходимо создать
связанное с ним поддерево.
Правая скобка - означает завершение выражения.
Операнд (цифра) – достигнут лист дерева или потомок.
Оператор (знак операции) – должен иметь двух потомков.

19.

19
Алгоритм создания дерева выражений.
Определим алгоритмы, которые должны выполняться при получении каждого из
приведенных символов:
1. Если считан символ левая скобка: создать новый узел, как левого потомка текущего
узла и сделать его текущим.
2. Если считан оператор ('+' или '-' или '/' или '*'):
2.1. сделать текущим родительский узел, текущего узла и поместить в него оператор;
2.2. создать новый узел как правого потомка родительского узла и сделать новый
узел текущим;
3. Если считан операнд (число), то помещает это значение в текущий узел.
4. Если считан символ правая скобка, то перемещаемся к родителю текущего узла
Пример. Построение дерева синтаксического разбора выражения ((5 - (2*4)))

20.

20
Алгоритм создания дерева выражений.
Сформируем алгоритм построения дерева разбора, исходя из проведенной трассировки
построения.
Дано. Выражение, записанное в соответствии с правилом: цифра|(Формула оператор
Формула).
Результат. Дерево разбора (или дерево выражения).
Псевдокод алгоритма разбора. Используются функции АТД ВinTree
СreateTree(string str){
Tnode T, currentNode;
CreateNode(T); // создание корневого узла
пустого дерева
//разбор строки выражения
i=0;
currentNode=T;
do{
i=i+1;
if (str[i] -левая скобка){
CreateNode(LeftTree(currentNode));
currentNode= currentNode.LeftTree;
}
if (str[i] – цифра){
currentNode.data=str[i];
currentNode=Parent(currentNode);
}
if (str[i] - оператор){
currentNode.data=str[i];
CreateNode(currentNode.rightTree);
currentNode= currentNode.rightTree;
}
if (str[i] – правая скобка){
currentNode= Parent(currentNode);
}
}while currentNode не пусто.
return T;
}

21.

21
Структуры данных в оптимизации поиска. Массив данных,
упорядоченных по значениям ключей
Пусть имеется файл большого объема, требуется найти в нем запись. Записи файла
содержат ключи, по которым запись отыскивается.
Можно применить алгоритм поиска записи с ключом в файле. Но так как файл
организован последовательно, то применить придется алгоритм линейного поиска,
асимптотическая сложность которого O(n), где n количество записей в файле.
Можно оптимизировать поиск в файлах, используя известные алгоритмы в
упорядоченных массивах: бинарный поиск, поиск Фибоначчи, интерполяционный поиск,
асимптотическая сложность которых O(log n).
Далее мы рассмотрим динамические структуры поиска, которые позволяют вставлять
новые элементы, предварительно найдя им место в структуре, и удалять найденные данные
из структуры.

22.

22
Хеширование и его применение в алгоритмах поиска
Этот алгоритм относиться к поиску в динамических таблицах.
Хеш-таблица - это механизм, позволяющий обеспечит доступ к записи в таблице за
фиксированное время, т.е. O(1) в лучшем случае и O(n) в худшем случае.
Отображение это функция, определенная на множестве элементов (области
определения) одного типа и формирующая значение на множестве элементов (область
значений) другого типа.
Т.е. отображение можно представить М(d)=r, где d – ‘значение из области определения М,
а r значение из области значений.
Будем понимать под понятием хеширование - процесс преобразования ключа в индекс
массива, называемого хеш – таблицей.

23.

23
Хеш функция
Хеш функция – это алгоритм, осуществляющий процесс преобразования значения ключа
в индекс хеш–таблицы. Результат хеш - функции в теории хеширования называют просто
хеш.
Хеш–таблица – это массив определенного размера, в ячейках которого размещаются
элементы данных. Место (индекс элемента в таблице) для размещения данных в таблице,
вычисляет хеш-функция на основе значения ключа.

24.

24
Хеш функция
Пример. Пусть хеш-таблица имеет размер L=100
(по количеству сотрудников), хеш-функция h(key)
должна вырабатывать индекс в пределах от 1 до 100,
тогда алгоритм вычисления такого значения на основе
ключа может быть совершенно простым: key%L.
Пусть
имеется
список
ИНН
сотрудников:1111112311, 1111112312, 1111112302.
Тогда хеш–функция h(key) для ключа 1111112311
вернет индекс – 11, а это значит, что запись о
сотруднике с ИНН равным 1111112311 разместиться в
хеш-таблице под индексом 11. Соответственно запись с
ключом 1111112312 разместиться по индексу 12, а
1111112302 по индексу 2.
Пример хеш-таблицы с размещенными
ключами и данными

25.

25
Принцип однородного хеширования
Для успешного хеширования очень важно, чтобы хеш-функция создавала такие
индексы, что размещаемые в таблице данные были равномерно (однородно) распределены
по таблице. Т.е. созданный индекс не зависел от индексов с которыми хешированы другие
элементы.
Для применения хеширования необходимо:
•чтобы элементы, размещаемые в хеш-таблице, имели уникальный ключ;
•подобрать хеш-функцию, обеспечивающую принцип однородности.

26.

26
Коллизия - проблема хеш-таблицы
Коллизия – это ситуация, когда для разных ключей хеш-функция создает одинаковый индекс.
Поэтому процесс хеширования включает 2 этапа:
1) Вызывается хеш-функция, которая, оперируя с ключом, возвращает индекс в хештаблице.
2) Разрешение возникающей коллизии.
Коллизии для ключей
Для разрешения коллизий, которые возникают при
добавлении данных в хеш-таблицу, применяются два
метода организации хеш-таблиц:
- метод цепного хеширования;
- метод открытого адреса.
Цепное (сцепленное) хеширование формирование
цепочек из элементов, хешированных с одним
индексом.
Хеширование с открытым адресом таблица большого
объема в элементы которой записываются ключи и
данные.

27.

27
Метод цепного хеширования
Это один из способов разрешения коллизий, когда элементы, ключи которых получили один
индекс, хранятся в одном однонаправленном списке, а вершина этого списка хранится в хештаблице. Тогда хеш-таблица – это массив указателей на вершины списков.

28.

28
Метод цепного хеширования
Пример.
Создание
хеш–таблицы,
использующей динамические списки для
устранения коллизий.
Создадим хеш-таблицу для ключей: 111001,
111205, 111312, 114101, 111412, 111313,
111305.
Хеш-таблица, организована по методу
цепочек для разрешения коллизий

29.

29
Проблемы хеш-таблицы, реализующей разрешение коллизии
по методу цепочек
1. Проблема однородного хеширования
Хеш функция должна удовлетворять принципу однородного хеширования. Т.е. желательно,
чтобы списки были примерно одной длины. При большом количестве элементов в списках
теряется смысл хеширования – «доступ к любому элементу в таблице за фиксированное
время», так как поиск приведет к линейному перебору длинного списка. Нет функций,
которые удовлетворяли бы принципу однородного хеширования для всех разрабатываемых
приложений.

30.

30
Проблемы хеш-таблицы, реализующей разрешение коллизии
по методу цепочек
2. Проблема размера таблицы
Если создать таблицу сразу большого размера, то многие элементы могут просто не
использоваться. Лучше создать таблицу из нескольких элементов и, по мере увеличения
числа вставляемых элементов, ее увеличивать.
Поэтому вводится коэффициент нагрузки хеш-таблицы: это отношение количества
размещенных в хеш таблице записей с данными к длине таблицы (размеру массива).
Коэффициент нагрузки=count/L, где count – количество записей в таблице, L – длина
таблицы.
Если count/L>0,75, то следует увеличить размер таблицы вдвое, это гарантирует, что размер
списков будет небольшим, меньшим 1 (count=L*0,75).
Изменение размера таблицы влечет за собой повторное хеширование всех элементов из
списков в новую таблицу большего размера. Этот процесс называют рехешированием.

31.

31
Анализ сложности алгоритмов над таблицей цепного хеширования
Докажем¸ что цепное хеширование позволяет выполнить операции вставки, удаления и поиска
элемента за фиксированное время, т.е. время выполнения операции оценивается по нотации
«большое О» как О(1).
Для доказательства, введем обозначения:
n - это количество элементов размещенных в таблице;
m - размер таблицы (количество списков).
В качестве критерия оценки времени выполнения операций будем использовать количество
выполняемых итераций - сравнений.

32.

32
Анализ сложности алгоритмов над таблицей цепного хеширования
Операция поиска.
Данная операция связана с тем, что задается ключ поиска, хеш-функция вычисляет индекс для
хеш-таблицы и далее выполняется поиск в списке этого индекса.
Средний размер списка не должен превышать 0,75 (согласно правилу создания хеш таблицы).
т.е. потребуется 0,75 итераций. Следовательно, среднее время в лучшем и худшем случаях
будет постоянным и может быть вычислено так:
Оср(n,m)наилучшем случае=n/(2m) при удвоенном размере таблицы
Оср(n,m)наихудшем случае=n/m
Таким образом,. время выполнения операции поиска зависит не от n (количества размещенных
элементов), а от отношения n/m, а, следовательно, его можно аппроксимировать как О(1).

33.

33
Анализ сложности алгоритмов над таблицей цепного хеширования
Операция удаления.
Данная операция состоит из двух алгоритмов:
Поиск элемента с заданным ключом.
Непосредственно удаление элемента из списка.
Для поиска элемента требуется время, определяемое как О(1). Для удаления элемента из
списка требуется также время, определяемое как О(1). Эти две операции будут выполняться
последовательно, согласно правилу суммы, время выполнения операции удаления так же
определяется как О(1).

34.

34
Анализ сложности алгоритмов над таблицей цепного хеширования
Операция вставки нового элемента в хеш-таблицу.
Данная операция включает алгоритмы:
Выполнение хеш-функции
Вставка нового элемента в список.
Оба алгоритма выполняются за время О(1). Тогда и весь алгоритм так же за О(1). Но это
справедливо для таблицы с однородным распределением элементов, которое поддерживается
правилом рехеширования. Время рехеширования будет зависеть от n, но рехеширование
выполняется один раз на 2m вставок, а, следовательно, будет постоянным т.е. О(1). При
выполнении операций вставки и только в случае рехеширования время будет большим.

35.

35
Метод хеширования с открытым адресом
Другой метод разрешения коллизий – это организация таблицы с открытым адресом. В этом
случае все элементы хранятся непосредственно в хеш-таблице, без использования связных
списков.
Суть метода
Значение вставляется непосредственно в открытый адрес.
Алгоритм операции вставки значения в таблицу:
1. Хеш-функция определяет индекс элемента в таблице в соответствии со значением
ключа вставляемого значения;
2. Выполняется проверка элемента таблицы с вычисленным индексом (открыта или
закрыта):
2.1. Если элемент таблицы открыт, то значение вставляется в этот элемент таблицы;
2.2. Если элемент таблицы закрыт, то выполняется процесс разрешения коллизии.
(Под термином «значение» будем понимать данные, вставляемые в таблицу и содержащие ключ и связанные с ним
данные)

36.

36
Метод хеширования с открытым адресом
Алгоритмы разрешения коллизии при применении метода хеширования с открытым адресом:
Последовательный поиск
При попытке добавить элемент в занятую ячейку i начинаем
последовательно просматривать ячейки i+1,i+2,i+3
Линейный поиск
Выбираем шаг q. При попытке
добавить элемент в занятую
ячейку
i
начинаем
последовательно
просматривать ячейки i+(1⋅q),
i+(2⋅q), i+(3⋅q) и так далее, пока
не найдём свободную ячейку.
Квадратичный поиск
Шаг q не фиксирован, а изменяется квадратично: q = 1, 4, 9, 16....
Соответственно при попытке добавить элемент в занятую ячейку i
начинаем последовательно просматривать ячейки i+1,i+4,i+9 и так
далее, пока не найдём свободную ячейку.

37.

37
Метод хеширования с открытым адресом
Пусть в создаваемую хеш-таблицу надо вставить следующие данные:
Создадим хеш-таблицу с открытым адресом из 100 элементов. Хеш-функция определяет
индекс по формуле key%100.

38.

38
Операция вставки записи в хеш-таблицу с открытым адресом
Для проверки открыт адрес в
таблице или нет напрашивается
операция контроля ключа. Чтобы
алгоритм был не зависим от типа
ключа, (т.е. не контролировать
значение) удобно добавить в
таблицу еще одно поле – признак
свободной ячейки. Например, это
поле может быть логического типа,
тогда
значение
true,
будет
указывать на то, что адрес открыт, а
значение false на то, что адрес
закрыт.

39.

39
Операция вставки записи в хеш-таблицу с открытым адресом
Структура элемента хеш-таблицы
Реализация алгоритма операции вставки на языке С++ может быть такой:

40.

40
Алгоритм операции поиска ключа в хеш-таблице с открытым адресом
Эта операция имеет следующий алгоритм:
1. Получение ключа поиска К.
2. Определение индекса элемента в таблице по ключу К посредством хеш – функции,
которая использовалась при вставке значений в таблицу.
3. Проверка, содержит ли элемент, ключ поиска:
3.1. если этот элемент содержит введенный ключ, то поиск завершается и возвращаются
данные записи;
3.2. если элемент таблицы по этому индексу не содержит заданный ключ и индекс не
вышел за границу таблицы, то осуществляется алгоритм подбора нового индекса по тому
же алгоритму, который использовался при выполнении операции вставки в случае
коллизии (например, подбор со смещением 1), пока не будет найден элемент с таким
ключом, или не будет найден открытый адрес. Если найден открытый адрес, то это
означает, что такого ключа в таблице нет.
Например, найти элемент с ключом 304002 или с ключом 507002 в таблице на слайде 38.

41.

Алгоритм операции удаления значения из хеш-таблицы с открытым
адресом
41
1
2
3
Получение ключа К, удаляемой записи.
Поиск элемента таблицы, содержащей ключ К.
Если элемент с ключом К найден, то надо выполнить удаление значения из таблицы.
Удалим из представленной
таблицы значение с ключом
304002.
Теперь найдем запись с
ключом 305002.
Запись найдена не будет.
индекс
1
2
3
4
5
6
7
8
9
10
11
……….
100
ключ
111001
111002
112001
212001
303002
304002
111007
305002
фамилия
Иванов
Петров
Волков
Лисицын
Жаворонков
Медведев
Сидоров
Рыбин
303010
Акулов
………..
…………….
Признак открытого адреса
false
false
false
false
false
true
false
false
true
false
true
true
True

42.

42
Алгоритм операции удаления значения из хеш-таблицы с открытым
адресом
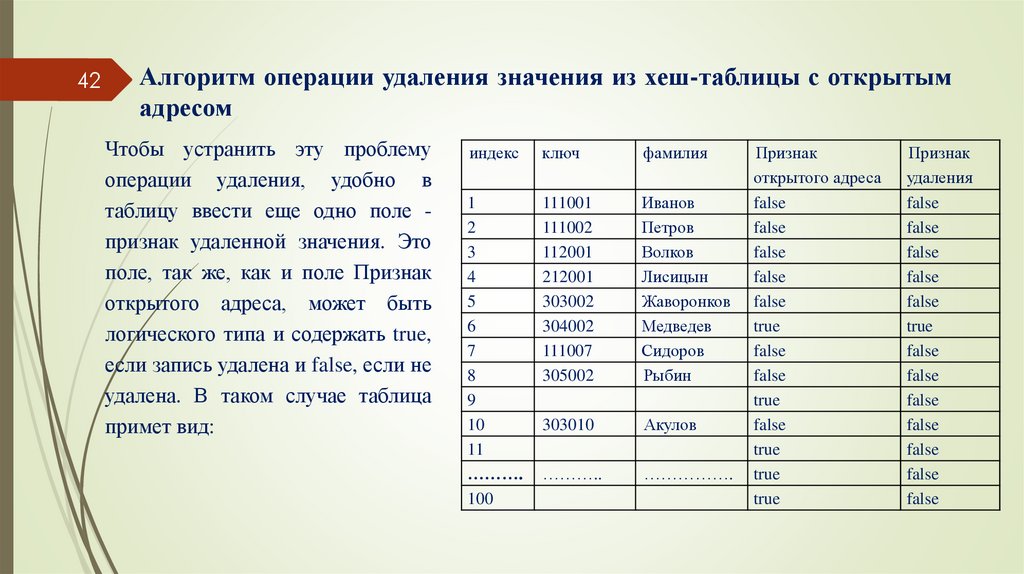
Чтобы устранить эту проблему
операции удаления, удобно в
таблицу ввести еще одно поле признак удаленной значения. Это
поле, так же, как и поле Признак
открытого адреса, может быть
логического типа и содержать true,
если запись удалена и false, если не
удалена. В таком случае таблица
примет вид:
индекс
ключ
фамилия
1
2
3
4
5
6
7
8
9
10
11
……….
100
111001
111002
112001
212001
303002
304002
111007
305002
Иванов
Петров
Волков
Лисицын
Жаворонков
Медведев
Сидоров
Рыбин
303010
Акулов
………..
…………….
Признак
открытого адреса
false
false
false
false
false
true
false
false
true
false
true
true
true
Признак
удаления
false
false
false
false
false
true
false
false
false
false
false
false
false

43.

43
Алгоритм операции удаления значения из хеш-таблицы с открытым
адресом
В связи с этими изменениями таблицы, изменится алгоритм поиска записи по ключу.
При поиске записи с заданным ключом, в случае свободной ячейки надо проверять и
значение поля Признак удаления.
Структура элемента таблицы
Алгоритм поиска элемента с
заданным ключом в таблице
с открытым адресом,
имеющей поля с признаками
свободного адреса и
удаленного значения на
языке С++.

44.

44
Проблемы хеширования с открытым адресом
2) Первичная кластеризация
Кластер — это последовательность непустых позиций в таблице по пути поиска открытого
для вставки адреса или при поиске ключа. При добавлении нового элемента в кластер он не
только становится длиннее, но и растет быстрее. Так как ключи, хешированные с новым
индексом, будут следовать по тому же пути, что и те, что уже вставлены в него.
Первичная кластеризация – это явление, которое происходит, когда обработчик коллизий
создает условие роста кластера. Обработчик коллизий со смещением 1 способствует
первичной кластеризации. Первичная кластеризация порождает длинные пути.
Попытка избежать появление кластеров – выбрать другое значение смещения, например, 20.
Но тогда ключи, хешированные с индексом ind, будут перекрывать путь, занимаемый
ключами: ind+20, ind+40, ind+60 и т.д. Но такое смещение порождает еще большую проблему,
чем первичная кластеризация.

45.

45
Двойное хеширование
Для устранения первичной кластеризации надо сделать смещение, зависимым от ключа, т.е.
получать его тоже с помощью хеш-функции.
Например, индекс вычислять по формуле key % m, а смещение по формуле key/m.
Рассмотрим пример (размер таблицы m=19)
Рассмотрим процесс вставки значений в таблицу и как
key
Key % m Key / m
реализуются коллизии.
33
14
1
1) Вставляется запись с ключом key=33 в элемент таблицы
72
15
3
с индексом 14.
71
14
3
2) Вставляется запись с ключом key=72 в элемент таблицы
112
17
5
с индексом 15.
56
18
2
3) Вставляется запись с ключом key=71 в элемент таблицы
109
14
5
с индексом 14, но этот элемент занят, тогда надо
реализовать
коллизию.
При
этом
индекс
рассчитывается по формуле (14+3)%m, что равно 17.
Т.е. 71 вставляется в элемент с индексом 17.
4) И т.д.