(7.2) 10_Nonstationary_Eq_Sch_Free_particle (2)

1.

Расплывание волнового пакета
Найти волновую функцию свободной частицы в произвольный момент времени если
начальное состояние описывается «гауссовой» функцией
ip0 x x 2
( x, t 0) ( x)
exp
2
2 1/ 4
2a
a
1
Нестационарное уравнение Шрёдингера
( x, t ) pˆ 2
i
( x, t )
t
2m
Искать решение в виде произведения
( x, t ) f t ( x)
НЕЛЬЗЯ!
Надо воспользоваться общим решением нестационарного уравнения Шрёдингера!

2.

Общее решение нестационарного уравнения Шрёдингера
в случае дискретного спектра энергии
iEnt
( x, t ) an n ( x)exp
n
an dx n x x
Как «модифицировать» выражение для общего решения в случае непрерывного спектра?

3.

Общее решение нестационарного уравнения Шрёдингера
в случае свободной частицы (непрерывный спектр энергии)
iE p t
( x, t ) dpa p p ( x)exp
a p dx p x x
Найти явный вид интеграла, определяющий волновую функцию?

4.

Промежуточные формулы
e ipx / 1
ip0 x x 2
eipx /
p x
, a p dx
exp
2
1/
4
2a
2
2 a 2
Явный вид интеграла, определяющий волновую функцию
ipx /
ipx /
2
2
ip
x
e
1
x
e
ip
t
0
( x, t ) dp dx
exp
2
exp
1/ 4
2
2
a
2
m
2
2
a

5.

Результат из «прошлого»
1/ 4
a
ap 2
2
p p0 2 a 2
exp
2
2
Или
1/ 4
a
( x, t ) 2
2
2 2
2
p
p
a
1
ipx
ip
t
0
dp exp
2
2
2m
2
Нашей конечной целью является плотность распределения вероятности
x, t ( x, t )
2
которая сама будет гауссовой функцией. Поэтому удобно воспользоваться следующим
приёмом: найти показатель экспоненты волновой функции, не интересуясь коэффициентом
перед экспонентой. Возведение модуля волновой функции в квадрат сводится к вычислению
удвоенной реальной части показателя экспоненты в волновой функции. Коэффициент перед
экспонентой в функции распределения найти из условия нормировки.
Полезная формула
2
dx
exp
px
qx
p2
exp
q
4q

6.

Промежуточная формула
2 a2
ix p0 a 2 p02 a 2
it
dp exp p 2 2 2m p 2 2 2
( x, t )
Или
ix p a 2 2
0
2
2 2
p0 a
( x, t ) exp g ( x) exp
2
2
a
it 2
4 2
2
2m
Вычислить
g ( x) g ( x) ?

7.

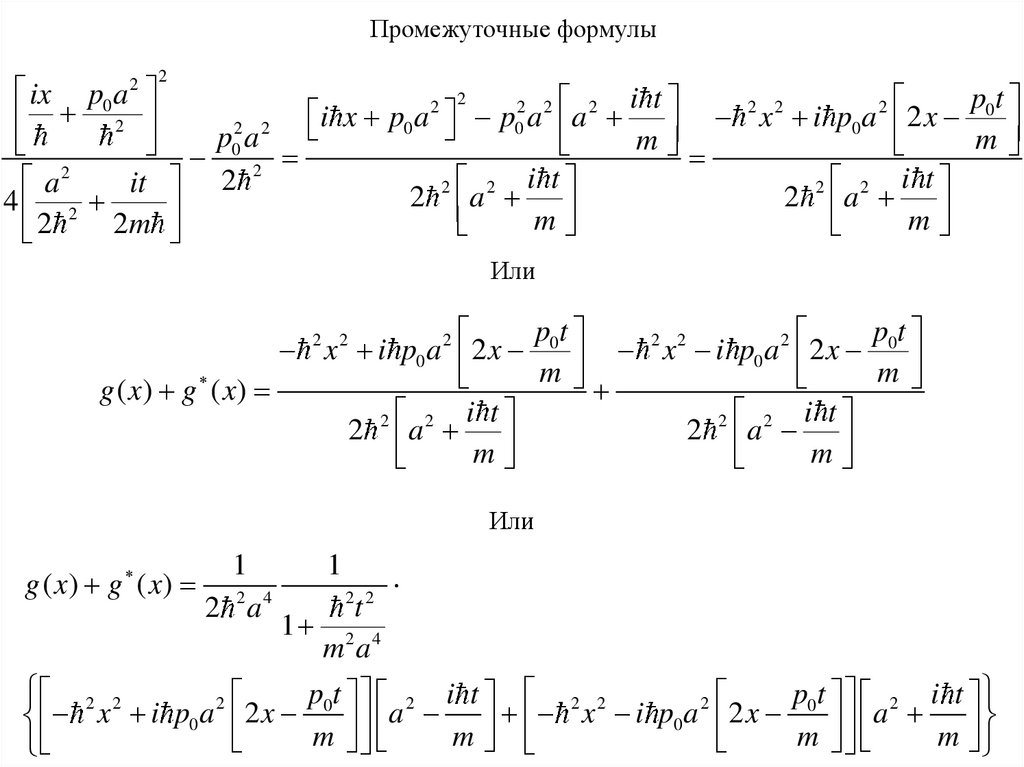
Промежуточные формулы
2
ix p0 a
p0t
i t
2 2
2
2 2
2 2 2
x
i
p
a
2
x
i
x
p
a
p
a
a
2
2 2
0
0
0
p
a
m
m
0
2
i t
i t
a2
it 2
2 2
2 2
2
a
2
a
4 2
m
m
2
2
m
2
Или
p0t
p0t
2 2
2
x i p0 a 2 x
x i p0 a 2 x
m
m
g ( x) g ( x)
i t
i t
2 2 a2
2 2 a2
m
m
2
2
2
Или
1
g ( x) g ( x) 2 4
2 a
1
1
2 2
t
m2 a 4
2 2
p0t 2 i t 2 2
p0t 2 i t
2
2
x
i
p
a
2
x
a
x
i
p
a
2
x
a
0
0
m
m
m
m

8.

Промежуточные формулы (продолжение)
2
p
t
p
t
2 2
2
0
0
2 a x 2 x
m
m
Поэтому
2
p0t
x
m
g ( x) g ( x)
2 2
t
2
a 2 2
ma
Плотность вероятности
2
p0t
x
m
( x, t ) A exp
2 2
t
2
a
2 2
m
a
Нормировочный множитель?

9.

Плотность вероятности
2
p0t
x
2 2
1
m
2
2
, t a t
( x, t )
exp
2
2 2
2
t
m
a
t
Время «расплывания» волнового пакета
( x, t 0)
a
2 2
( x, t )
2
2
2 2
t
a2 2 2
ma
x0
ma
2
a
2
ma 2
p0t
m
Следствие принципа соответствия: среднее значение координаты
зависит от времени по закону классической механики!

10.

Оценить время «расплывания» волнового пакета?
«Советская копейка»
10 27 erg second , m 1 gram, a 1 centimeter
Электрон в атоме
10 27 erg second , m 10 27 gram, a 10 8 centimeter