Similar presentations:
Кодирование и декодирование информации. Условие Фано. Подготовка к ЕГЭ (10 класс)
1.
ИнформатикаПодготовка к ЕГЭ
Условие ФАНО
Кодирование и декодирование информации
Условие Фано
Теория
Задачи с
решением
2.
ТеорияКодирование и
декодирование
Прямое
условие Фано
Обратное
условие Фано
Декодирование
информации
Построение
дерева Фано
Дерево для
двоичного кода
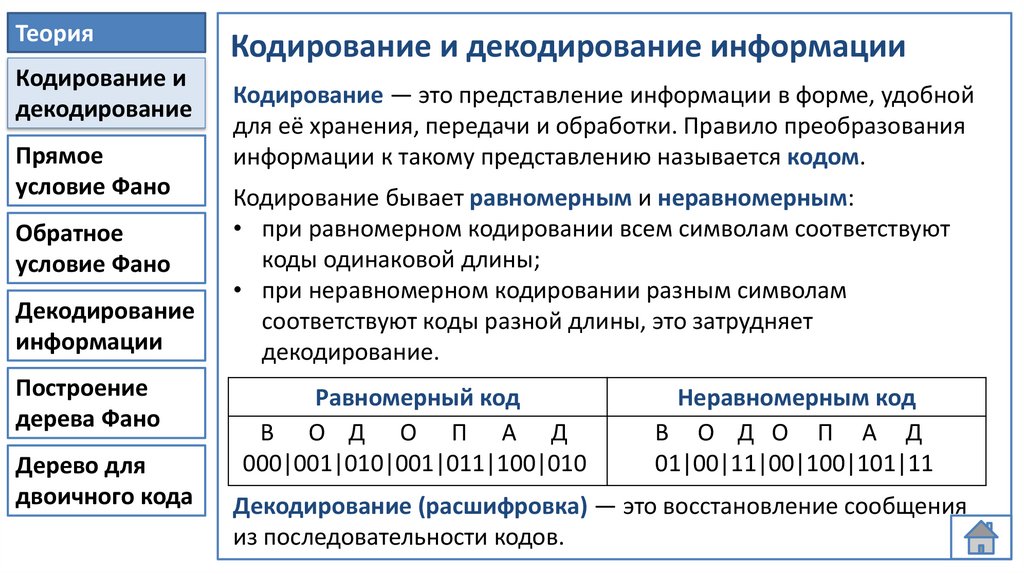
Кодирование и декодирование информации
Кодирование — это представление информации в форме, удобной
для её хранения, передачи и обработки. Правило преобразования
информации к такому представлению называется кодом.
Кодирование бывает равномерным и неравномерным:
• при равномерном кодировании всем символам соответствуют
коды одинаковой длины;
• при неравномерном кодировании разным символам
соответствуют коды разной длины, это затрудняет
декодирование.
Равномерный код
В О Д О П А Д
000|001|010|001|011|100|010
Неравномерным код
В О Д О П А Д
01|00|11|00|100|101|11
Декодирование (расшифровка) — это восстановление сообщения
из последовательности кодов.
3.
ТеорияНеравномерные коды. Прямое условие Фано
Кодирование и
декодирование
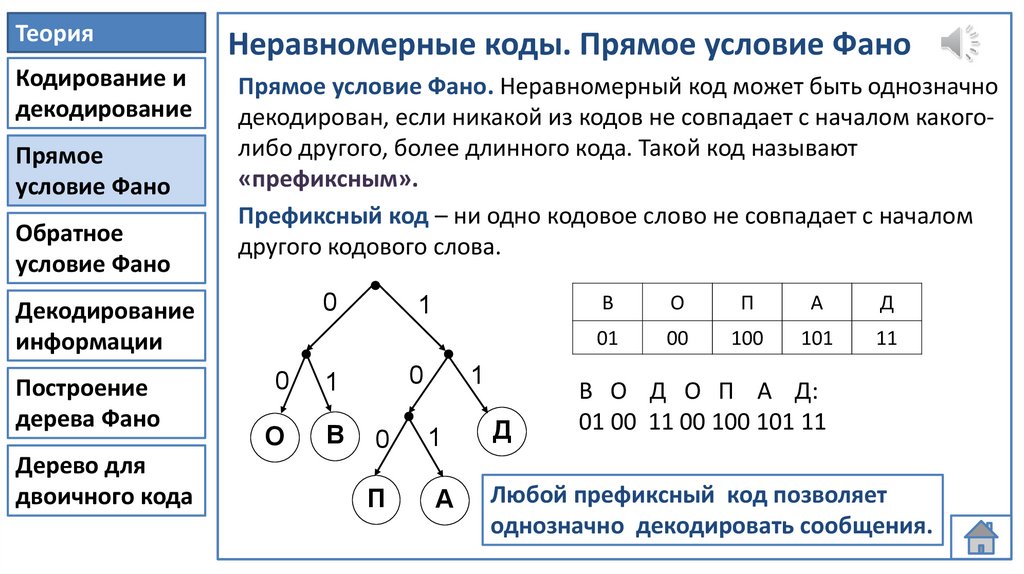
Прямое условие Фано. Неравномерный код может быть однозначно
декодирован, если никакой из кодов не совпадает с началом какоголибо другого, более длинного кода. Такой код называют
«префиксным».
Префиксный код – ни одно кодовое слово не совпадает с началом
другого кодового слова.
Прямое
условие Фано
Обратное
условие Фано
0
Декодирование
информации
Построение
дерева Фано
Дерево для
двоичного кода
0
1
О
В
1
0
1
В
О
П
А
Д
01
00
100
101
11
В О Д О П А Д:
01 00 11 00 100 101 11
0
1
Д
П
А
Любой префиксный код позволяет
однозначно декодировать сообщения.
4.
ТеорияКодирование и
декодирование
Неравномерные коды. Обратное условие Фано
Прямое
условие Фано
Обратное условие Фано. Неравномерный код может быть
однозначно декодирован, если никакой из кодов не совпадает с
окончанием какого-либо другого, более длинного кода. Такой
код называют «постфиксным».
Обратное
условие Фано
Постфиксный код – ни одно кодовое слово не совпадает с концом
другого кодового слова
Декодирование
информации
Постфикс = окончание слова.
Построение
дерева Фано
Дерево для
двоичного кода
В
10
О
00
П
1101
А
001
Д
0101
Любой постфиксный код позволяет однозначно декодировать
сообщения (с конца).
5.
ТеорияКодирование и
декодирование
Прямое
условие Фано
Обратное
условие Фано
Декодирование
информации
Построение
дерева Фано
Дерево для
двоичного кода
Декодирование информации
Для однозначного декодирования достаточно выполнения хотя бы
одного из двух условий Фано:
• при выполнении прямого условия Фано последовательность
кодов однозначно декодируется с начала;
• при выполнении обратного условия Фано последовательность
кодов однозначно декодируется с конца.
6.
ТеорияКодирование и
декодирование
Прямое
условие Фано
Обратное
условие Фано
Декодирование
информации
Построение
дерева Фано
Дерево для
двоичного кода
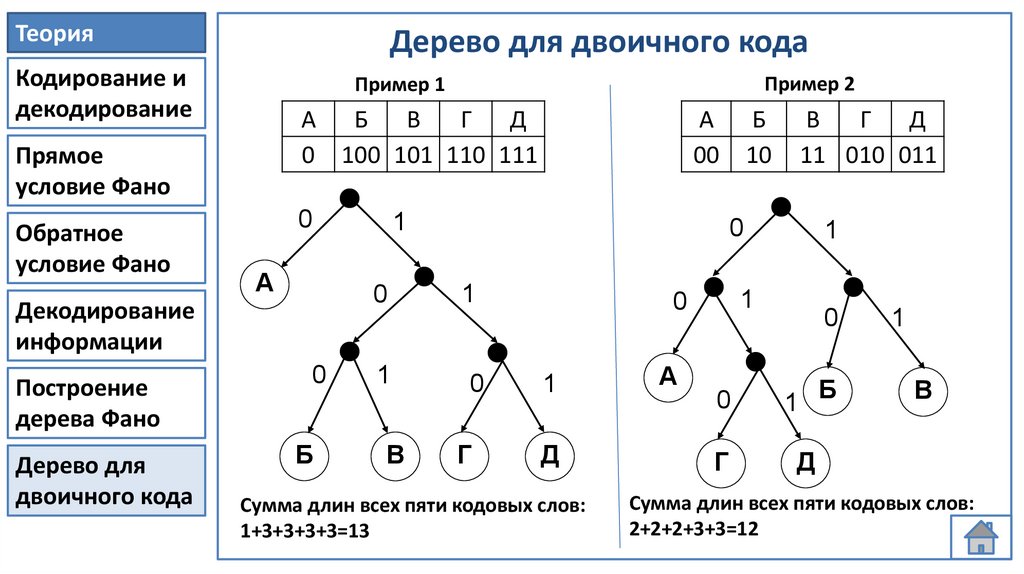
Построение дерева Фано
Дерево Фано – это удобный и наглядный способ решения задач,
связанных с подбором неравномерных двоичных кодов.
Основные принципы построения дерева Фано:
0
1
1. Каждый узел дерева Фано имеет ровно две ветви, при этом
одной ветви (например, левой) сопоставляется 0, а другой
0 1 0 1
ветви (правой) –1.
2. От каждого направления можно также рисовать только два
В А Б
0
1
направления: 0 (ноль) и 1 (единицу) и т.д. Получается
структура похожая на дерево!
Г
Д
3. В конце каждой ветки ( т.е. на «листьях») располагаются
буквы.
А
Б
В
Г
Д
4. Если мы расположили на «листе» букву, то от этой
10 11 01 000 001
ветки нельзя делать новые ответвления.
5. Чем чаще встречается какой-либо символ, тем короче должен быть его код
и тем раньше этот символ надо поместить в дерево.
6. Для каждого символа код Фано получается последовательной записью всех
нулей и единиц по кратчайшему пути от вершины дерева к
соответствующему символу.
7.
ТеорияДерево для двоичного кода
Кодирование и
декодирование
А Б
В
Г
Д
0 100 101 110 111
Прямое
условие Фано
Обратное
условие Фано
0
А
Декодирование
информации
Построение
дерева Фано
Дерево для
двоичного кода
Пример 2
Пример 1
0
Б
А
00
1
В
Г
Д
11 010 011
0
0
1
1
0
1
Г
Д
В
Б
10
1
0
Сумма длин всех пяти кодовых слов:
1+3+3+3+3=13
А
1
0
0
1
Г
Д
Б
1
В
Сумма длин всех пяти кодовых слов:
2+2+2+3+3=12
8.
Задача 1Задача 2
Задача 3
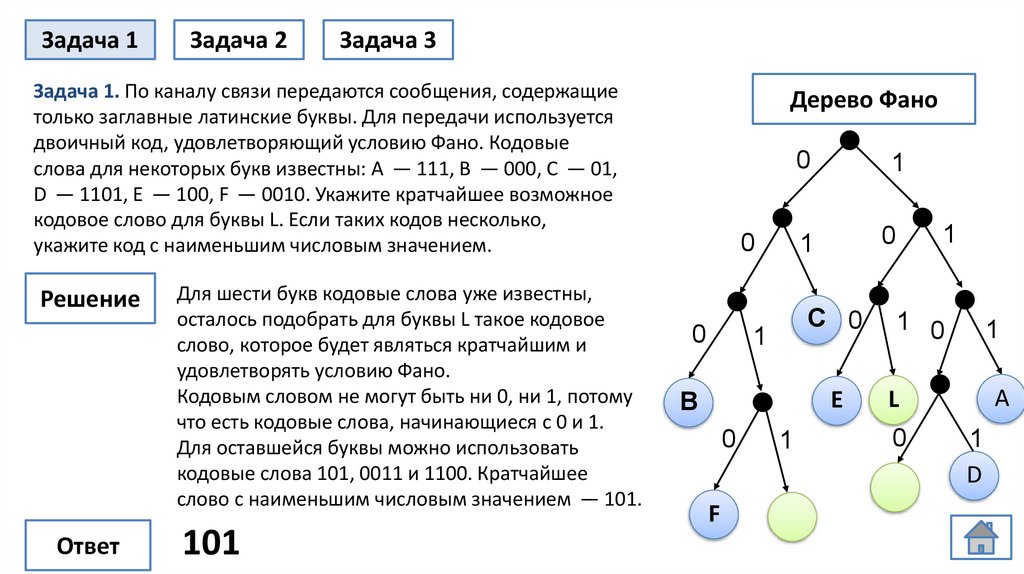
Задача 1. По каналу связи передаются сообщения, содержащие
только заглавные латинские буквы. Для передачи используется
двоичный код, удовлетворяющий условию Фано. Кодовые
слова для некоторых букв известны: A — 111, B — 000, С — 01,
D — 1101, E — 100, F — 0010. Укажите кратчайшее возможное
кодовое слово для буквы L. Если таких кодов несколько,
укажите код с наименьшим числовым значением.
Решение
Ответ
Для шести букв кодовые слова уже известны,
осталось подобрать для буквы L такое кодовое
слово, которое будет являться кратчайшим и
удовлетворять условию Фано.
Кодовым словом не могут быть ни 0, ни 1, потому
что есть кодовые слова, начинающиеся с 0 и 1.
Для оставшейся буквы можно использовать
кодовые слова 101, 0011 и 1100. Кратчайшее
слово с наименьшим числовым значением — 101.
101
Дерево Фано
0
0
0
1
1
0
С 0
1
В
Е
0
F
1
1
1 0
1
L
0
0
А
1
D
9.
Задача 1Задача 2
Задача 3
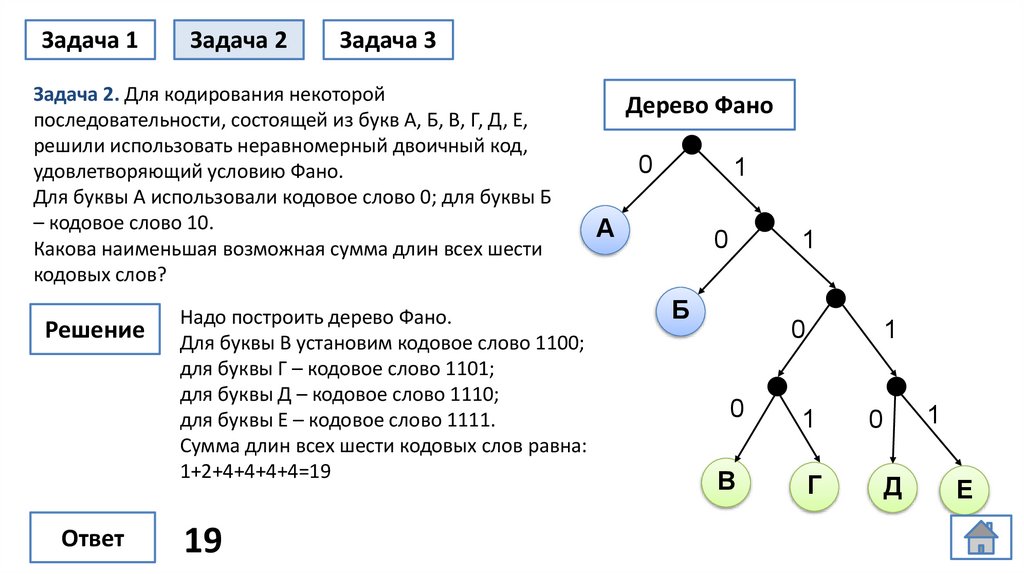
Задача 2. Для кодирования некоторой
последовательности, состоящей из букв А, Б, В, Г, Д, Е,
решили использовать неравномерный двоичный код,
удовлетворяющий условию Фано.
Для буквы А использовали кодовое слово 0; для буквы Б
– кодовое слово 10.
Какова наименьшая возможная сумма длин всех шести
кодовых слов?
Решение
Ответ
Надо построить дерево Фано.
Для буквы В установим кодовое слово 1100;
для буквы Г – кодовое слово 1101;
для буквы Д – кодовое слово 1110;
для буквы Е – кодовое слово 1111.
Сумма длин всех шести кодовых слов равна:
1+2+4+4+4+4=19
19
Дерево Фано
0
1
А
1
0
Б
0
1
0
1
В
Г
1
0
Д
Е
10.
Задача 1Задача 2
Задача 3
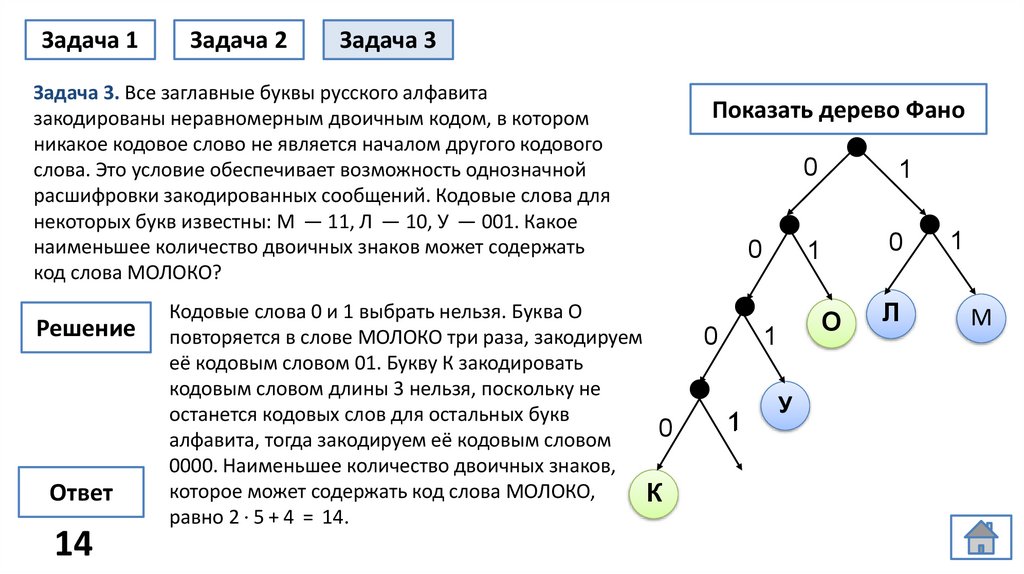
Задача 3. Все заглавные буквы русского алфавита
закодированы неравномерным двоичным кодом, в котором
никакое кодовое слово не является началом другого кодового
слова. Это условие обеспечивает возможность однозначной
расшифровки закодированных сообщений. Кодовые слова для
некоторых букв известны: М — 11, Л — 10, У — 001. Какое
наименьшее количество двоичных знаков может содержать
код слова МОЛОКО?
Решение
Ответ
14
Кодовые слова 0 и 1 выбрать нельзя. Буква О
повторяется в слове МОЛОКО три раза, закодируем
её кодовым словом 01. Букву К закодировать
кодовым словом длины 3 нельзя, поскольку не
останется кодовых слов для остальных букв
0
алфавита, тогда закодируем её кодовым словом
0000. Наименьшее количество двоичных знаков,
которое может содержать код слова МОЛОКО,
К
равно 2 · 5 + 4 = 14.
Показать дерево Фано
0
1
1
1
0
О
1
0
0
У
Л
1
М




 informatics
informatics








