Кодирование информации. Шифрование. Дешифрование

1. Кодирование информации

Презентация 10-2
КОДИРОВАНИЕ ИНФОРМАЦИИ

2. Шифрование. Дешифрование.

ШИФРОВАНИЕ. ДЕШИФРОВАНИЕ.
Шифрование – процесс применения шифра к
защищаемой информации, то есть преобразование
защищаемой информации в шифрованное сообщение
с помощью определенных правил, содержащихся в
шифре.
Дешифрование – процесс, обратный шифрованию, то
есть преобразование шифрованного сообщения в
защищаемую информацию с помощью определенных
правил, содержащихся в шифре.

3. Классические шифры

КЛАССИЧЕСКИЕ ШИФРЫ
Большое влияние на развитие криптографии оказали
появившиеся в середине прошлого века работы
американского математика Клода Шеннона. В этих
работах были заложены основы теории информации.
В своей работе «Математическая теория секретной
связи» Клод Шеннон обобщил накопленный до него
опыт разработки шифров. Оказалось, что даже в
сложных шифрах в качестве типичных компонентов
можно выделить шифры замены, шифры
перестановки или их сочетания.

4. Классические шифры

КЛАССИЧЕСКИЕ ШИФРЫ
Шифрами перестановки называются такие шифры,
преобразования из которых приводят к изменению
только порядка следования символов исходного
сообщения. Обычно открытый текст разбивается на
отрезки равной длины и каждый отрезок шифруется
независимо.
Шифрами замены называются такие шифры,
преобразования из которых приводят к замене
каждого символа открытого сообщения на другие
символы - шифробозначения, причем порядок
следования шифробозначений совпадает с порядком
следования соответствующих им символов открытого
сообщения.

5. Классические шифры

КЛАССИЧЕСКИЕ ШИФРЫ
Самые важные составляющие любого шифра – это
• общее правило, по которому преобразуется
исходный текст (алгоритм шифра);
• конкретная особенность именно этой серии
шифрованных сообщений (так называемый ключ)

6.

Задание

7.

Задание

8. Задача 1

ЗАДАЧА 1
Пусть для кодирования фразы «Доброе утро» выбран
такой код:
Д
О
Б
Р
Е
У
Т
Пробел
111 000 00
1
01
0
10
11

9.

Д
О
Б
Р
Е
У
Т
Пробел
111 000 00
1
01
0
10
11
Коды букв «сцепляются» в единую битовую строку и
передаются, например, по сети:
Доброе утро → 11100000100001110101000
В пункте назначения возникает проблема – как
восстановить исходное сообщение, и возможно ли это.
Раскодировать данное сообщение можно разными
способами. В том числе предположим, что оно состоит
только из букв Р – 1 и У – 0.
Тогда получим РРРУУУУУРУУУУРРРУРУРУУУ, т.е.
бессмысленный набор букв.

10.

Код называется однозначно декодируемым,
если любое кодовое сообщение можно
расшифровать единственным способом
(однозначно).
Код из задачи 1 не является однозначно
декодируемым.

11. Задача 2

ЗАДАЧА 2
Равномерные коды. Для той же фразы используем
равномерный код:
Д
О
Б
Р
Е
111 000 001 101 011
У
Т
Пробел
010 100 110

12.

Равномерные коды неэкономичны – гораздо длиннее
неравномерных. Это приводит к усложнению
кодирования, но при этом они раскодируются
однозначно, что, естественно, облегчает задачу.
Чтобы сократить длину сообщения, можно
попробовать применить неравномерный код, т.е. код,
в котором кодовые слова, соответствующие разным
символам исходного алфавита, могут иметь разную
длину, от одного до нескольких символов.

13. Задача 3

ЗАДАЧА 3
Д • Используем
О
Бследующий
Р код:Е
01
00
1011
100
У
Т
Пробел
1010 1101 1110 1111
0100101110000101011111101111010000
Эта битовая цепочка декодируется однозначно.
Первая буква - Д (код 01), т.к. ни одно другое кодовое
слово не начинается с 01. Вторая буква – О (код 00).
Никакое другое слово не начинается с 00. Это же
свойство, которое называется условием Фано,
выполняется и для кодовых слов других букв.

14. Условие Фано

УСЛОВИЕ ФАНО
Никакое кодовое слово не может
быть началом другого кодового слова.
Такие коды называются префиксными
(раскодируются с начала сообщения) и
декодируются однозначно.

15. Условие Фано

УСЛОВИЕ ФАНО
Примером кода, удовлетворяющего условию Фано,
являются телефонные номера в традиционной телефонии.
Если в сети существует номер 101, то номер 1012345 не
может быть выдан: при наборе трёх цифр АТС прекращает
понимать дальнейший набор и соединяет с адресатом по
номеру 101. Однако для набора с сотового телефона это
правило уже не действует, потому что требуется явное
завершение последовательности знаков соответствующей
кнопкой (обычно – с изображением зелёной трубки), при
этом 101, 1010 и 1012345 могут одновременно
пониматься как разные адресаты.

16. Задача 4

ЗАДАЧА
ЗАДАЧА44
Рассмотрим ещё один код:
Д О
Б
Р
Е
У
Т
Пробел
10 00 1011 001 0101 1000 0111 1111
Он не является префиксным, т.к. код буквы Д (10)
совпадает с началом кода буквы Б (1011), У(1000) и код
буквы О(00) совпадает с началом кода буквы Р (001).

17.

Д О
Б
Р
Е
У
Т
Пробел
10 00 1011 001 0101 1000 0111 1111
Закодируем наше сообщение:
ДОБРОЕ УТРО → 10 00 1011 001 00 0101 1111 1000
0111 001 00
Начнём раскодировать с начала. Первая – Д, или У, а
дальше идут вообще разные варианты: Р или Б… Т.е.
надо «заглядывать» вперёд, что очень неудобно.

18. обратное условие Фано

ОБРАТНОЕ УСЛОВИЕ ФАНО
Попробуем раскодировать сообщение с конца – оно
однозначно декодируется! Выполняется обратное
условие Фано:
никакое кодовое слово не совпадает с
окончанием другого кодового слова.
Коды, для которых выполняется обратное условие
Фано, называются постфиксными.

19. Сделаем вывод:

СДЕЛАЕМ ВЫВОД:
Сообщение декодируется однозначно,
если для используемого кода
выполняется прямое или обратное
условие Фано.

20.

Условие Фано - это достаточное, но не необходимое
условие однозначной декодируемости.
Это значит, что:
- для однозначной декодируемости достаточно
выполнения хотя бы одного из двух условий – прямого
или обратного.
- могут существовать коды, для которых не выполняется
ни прямое, ни обратное условие Фано, но тем не менее
обеспечивается однозначное декодирование, т.к. иначе
теряется смысл выражения.

21. Задача 5

ЗАДАЧА 5
Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д используется
неравномерный двоичный код, позволяющий однозначно
декодировать полученную двоичную последовательность.
Вот этот код: А – 00, Б – 01, В – 100, Г – 101, Д – 110.
Можно ли сократить для одной из букв длину кодового
слова так, чтобы код по-прежнему можно было
декодировать однозначно? Коды остальных букв меняться
не должны. Выберите правильный вариант ответа:
1) для буквы Д – 11
3) для буквы Г – 10
2) это невозможно
4) для буквы Д – 10

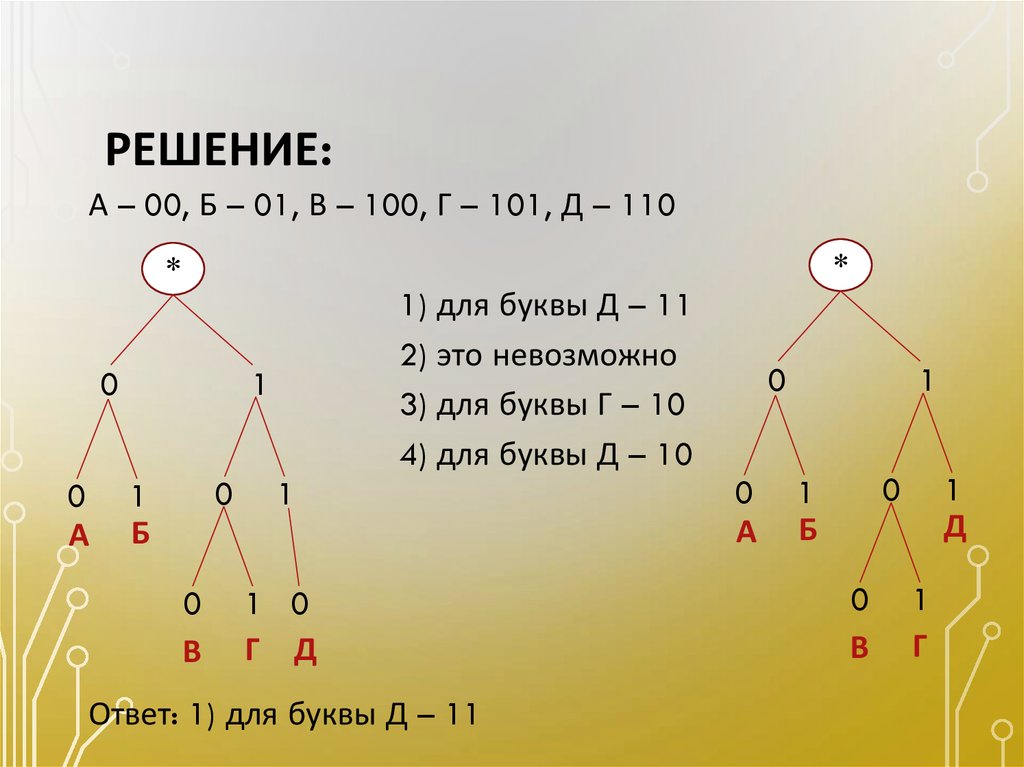
22. РЕШЕНИЕ:

А – 00, Б – 01, В – 100, Г – 101, Д – 110
*
*
0
0
А
1) для буквы Д – 11
2) это невозможно
3) для буквы Г – 10
4) для буквы Д – 10
1
0
1
Б
0
В
1
1 0
Г Д
Ответ: 1) для буквы Д – 11
0
0
А
1
0
1
Б
0
В
1
Д
1
Г

23. Задача 6

ЗАДАЧА 6
Для кодирования некоторой последовательности,
состоящей из букв К, Л, М, Н, решили использовать
неравномерный двоичный код, удовлетворяющий
условию Фано. Для буквы Н использовали кодовое слово
0, для буквы К – кодовое слово 10. Какова наименьшая
возможная суммарная длина всех четырёх кодовых слов?

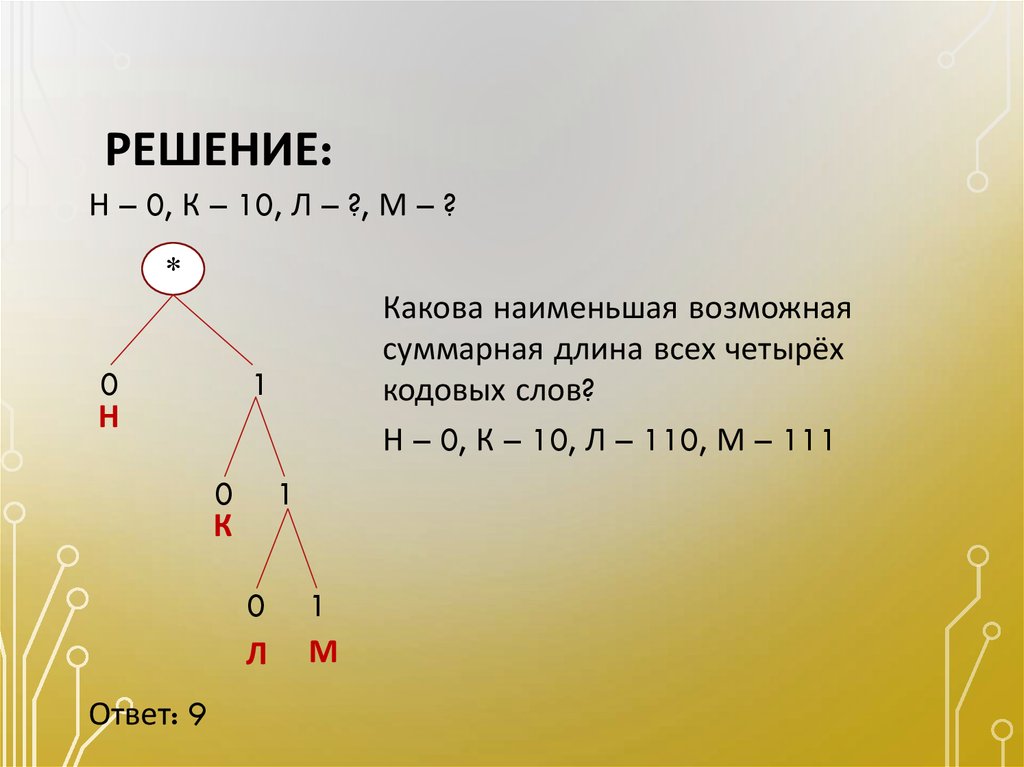
24. РЕШЕНИЕ:

Н – 0, К – 10, Л – ?, М – ?
*
0
Н
1
0
К
1
0
Л
Ответ: 9
Какова наименьшая возможная
суммарная длина всех четырёх
кодовых слов?
Н – 0, К – 10, Л – 110, М – 111
1
М

25. Задача 7

ЗАДАЧА 7
Для 5 букв латинского алфавита заданы их двоичные коды
(для некоторых букв из двух бит, для некоторых – из трех).
Эти коды представлены в таблице:
a
b
c
d
e
000 110 01 001 10
Какой набор букв закодирован двоичной строкой
1100000100110?

26. Задача 8

ЗАДАЧА 8
Для 5 букв латинского алфавита заданы их двоичные коды
(для некоторых букв – из двух бит, для некоторых – из
трех). Эти коды представлены в таблице:
a b c d e
100 110 011 01 10
Какой набор букв закодирован двоичной строкой
1000110110110? Все буквы в последовательности –
разные.

27. Задача 9

ЗАДАЧА 9
Для 6 букв латинского алфавита заданы их двоичные коды
(для некоторых букв из двух бит, для некоторых – из трех).
Эти коды представлены в таблице:
A
B
C
D
E
F
00 100 10 011 11 101
Какая последовательность из 6 букв закодирована
двоичной строкой 011111000101100?

28. Домашнее Задание

ДОМАШНЕЕ ЗАДАНИЕ
Решить задачи из презентации 10-2,
самостоятельная работа