Similar presentations:
Молекулярная физика (лекция № 5)
1.
Молекулярная физикаЛекция № 5
2.
План лекции:1. Опытное обоснование основных положений
молекулярно-кинетической теории. Масса и размеры
молекул. Постоянная Авогадро.
2. Идеальный газ. Основное уравнение молекулярнокинетической теории идеального газа. Температура и
ее измерение.
3. Уравнение состояния идеального газа (уравнение
Менделеева-Клапейрона).
4. Изотермический, изохорный и изобарный процессы.
5. Скорость молекул газа. Распределение Максвелла.
6. Соударения молекул. Средняя длина свободного
пробега.
7. Явления переноса.
3.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Молекулярная физика раздел физики,
изучающий строение и свойства вещества
исходя из молекулярно-кинетических
представлений, основывающихся на том,
что все тела состоят из молекул,
находящихся в непрерывном хаотическом
движении.
4.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
Демокрит
(460 370
до н. э.)
Михаил
Ломоносов
(1711 1765)
Джеймс
Максвелл
(1831 1879)
Рудольф
Клаузиус
(1822 – 1888)
Людвиг
Больцман
(1844 – 1906)
5.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Термодинамика раздел физики,
изучающий общие свойства
макроскопических систем, находящихся в
состоянии термодинамического
равновесия, и процессы перехода между
этими состояниями.
6.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Молекулярно-кинетическая теория
основана на следующих положениях:
Любое вещество состоит из атомов и
молекул.
Молекулы находятся в непрерывном
тепловом движении.
Между молекулами существуют силы
взаимодействия притяжения и
отталкивания.
7.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Под электронным микроскопом можно
рассмотреть и сфотографировать отдельные
крупные молекулы:
8.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Сжатие газов:
9.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
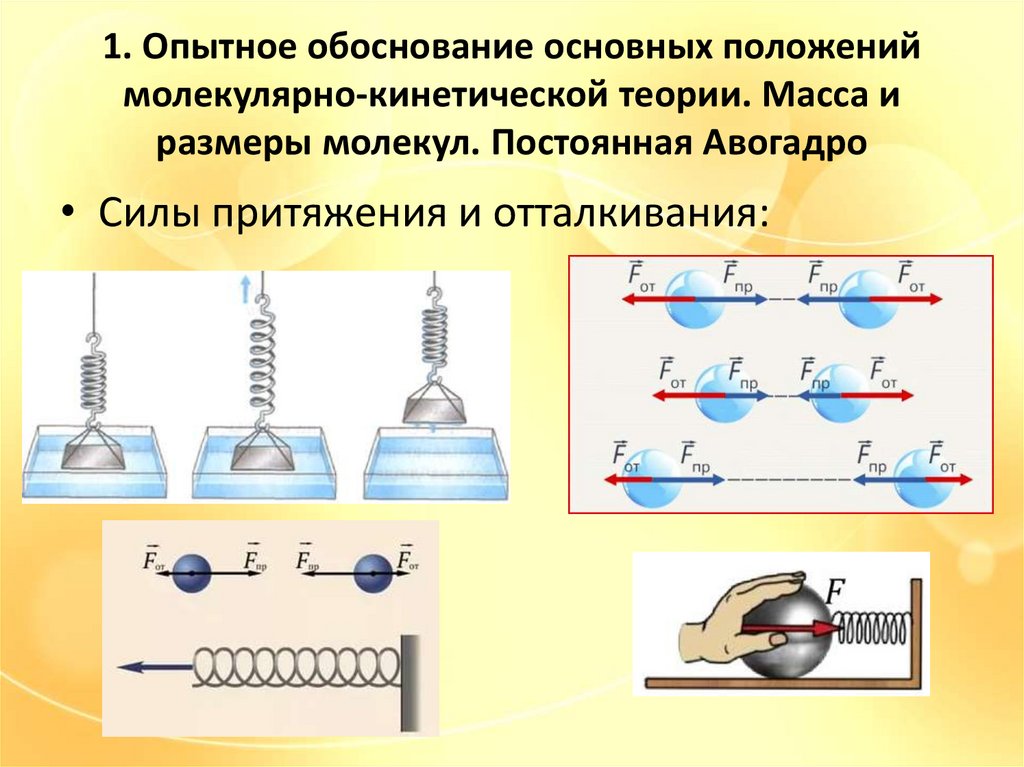
размеры молекул. Постоянная Авогадро
• Силы притяжения и отталкивания:
10.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Сварка, спайка и склейка твердых тел.
11.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
Опытными подтверждениями являются:
• броуновское движение хаотическое
непрерывное движение мелких частиц,
взвешенных в жидкости или газе,
обусловленное ударами молекул жидкости
(газа), окружающих их.
Роберт Броун
(1773 – 1858)
12.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
Опытными подтверждениями являются:
• диффузия процесс самопроизвольного
смешивания веществ, являющийся
результатом хаотического движения частиц.
13.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
Жан Батист
Перрен
(1870 – 1942)
• Перрен определил, что масса
молекулы кислорода почти в 200
млн. раз меньше массы
броуновской частицы и составляет
около 5 10-26 кг. Современное
значение массы молекулы
кислорода 5,31 10-26 кг.
• За атомную единицу массы
принимают 1/12 массы атома
углерода.
1а .е . м. 1,66 10 27 кг
14.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Масса молекулы m0:
m0 1,66 10 27 Mr , кг
• где Мr относительная молекулярная
масса, приводимая в таблице Менделеева.
• За единицу количества вещества моль,
принимают такое количество вещества, в
котором содержится число частиц, равное
числу атомов в 0,012 кг углерода.
N
0.012кг
23
6
.
02
10
1.66 10 27 12 кг
15.
1. Опытное обоснование основных положениймолекулярно-кинетической теории. Масса и
размеры молекул. Постоянная Авогадро
• Число частиц, содержащихся в одном моле,
называется постоянной Авогадро:
N A 6,02 1023 моль 1
Амедео Авогадро
(1776 – 1856)
16.
2. Идеальный газ. Основное уравнениемолекулярно-кинетической теории идеального
газа. Температура и ее измерение
• Идеальным называют газ, при описании
свойств которого делают следующие
допущения:
1) взаимодействие между молекулами
пренебрежимо мало;
2) размеры молекул не учитываются.
17.
2. Идеальный газ. Основное уравнениемолекулярно-кинетической теории идеального
газа. Температура и ее измерение
• Основное уравнение молекулярнокинетической теории газов:
2
p n0 E K
3
• где n0 концентрация (число молекул в
единице объема),
m
• E 2 средняя кинетическая энергия
поступательного движения молекул,
• среднее значение квадрата скорости
молекул.
2
0
K
2
18.
2. Идеальный газ. Основное уравнениемолекулярно-кинетической теории идеального
газа. Температура и ее измерение
• Абсолютная температура Т есть мера
средней кинетической энергии хаотичного
поступательного движения молекул:
3
E K kT
2
• где k 1,38 10 23 Дж / К постоянная
Больцмана.
• Связь между значениями температуры Т (в
кельвинах) и температуры t по Цельсию (в
градусах):
T t 273 ,15
o
19.
2. Идеальный газ. Основное уравнениемолекулярно-кинетической теории идеального
газа. Температура и ее измерение
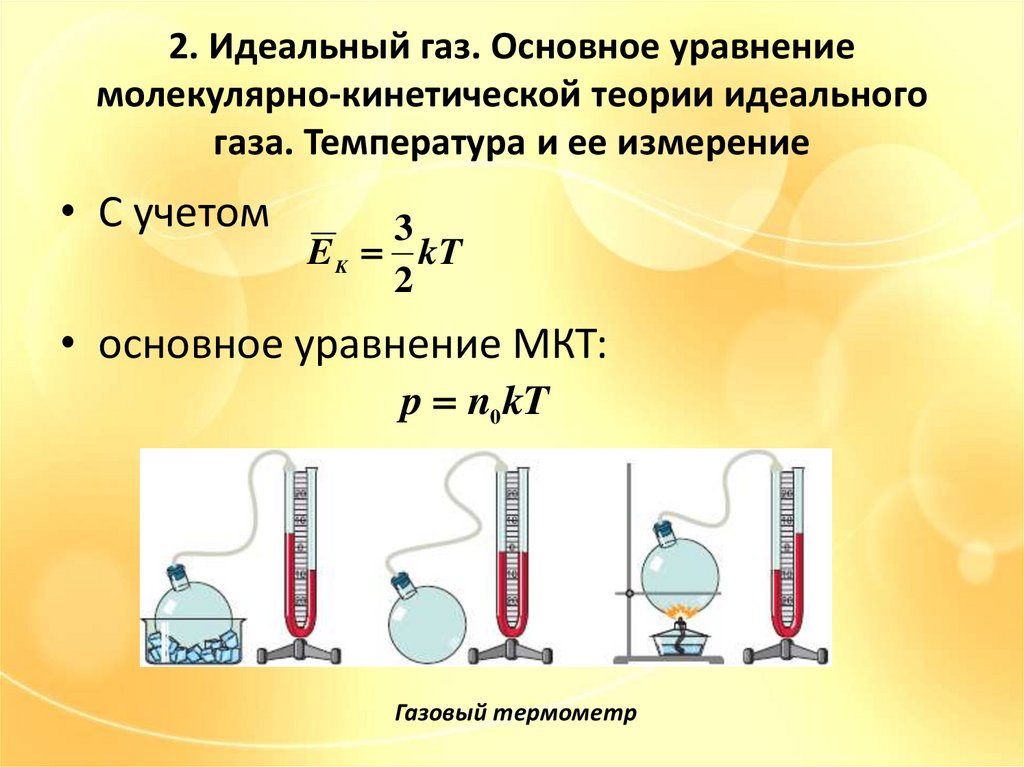
• С учетом
3
E K kT
2
• основное уравнение МКТ:
p n0 kT
Газовый термометр
20.
2. Идеальный газ. Основное уравнениемолекулярно-кинетической теории идеального
газа. Температура и ее измерение
m0
3
kT
2
2
2
2
3kT
m0
3kT
m0 называется
• Величина
среднеквадратичной скоростью.
При нормальных условиях
среднеквадратичная скорость молекул азота
около 500 м/с, водорода около 1800 м/с.
2
КВ
21.
3. Уравнение состояния идеального газа(уравнение Менделеева-Клапейрона)
• p n0 kT
умножим на V:
pV NkT
• где N n0V полное число молекул.
• Число молекул N N A произведение
числа молей газа на число молекул в
одном моле NA.
pV N A kT
• Универсальная газовая постоянная:
R N A k 8,31 Дж / моль К
22.
3. Уравнение состояния идеального газа(уравнение Менделеева-Клапейрона)
• Уравнение состояния:
pV RT
• Число молей:
Дмитрий
Менделеев
(1834 – 1907)
m
M
• Уравнение состояния
идеального газа (уравнение
Менделеева-Клапейрона):
m
pV
RT
M
Бенуа
Клапейрон
(1799 – 1864)
23.
3. Уравнение состояния идеального газа(уравнение Менделеева-Клапейрона)
• Уравнение состояния:
p V R T
p V
R
T
• Универсальная газовая постоянная
численно равна работе при изобарном
расширении одного моля идеального газа
при нагревании его на 1 К.
24.
4. Изотермический, изохорный иизобарный процессы
• Термодинамические процессы,
протекающие при неизменном значении
одного из параметров, называются
изопроцессами.
• Из уравнения состояния для одного моля
газа:
pV RT
25.
4. Изотермический, изохорный иизобарный процессы
• Изотермический процесс (T const) pV const
( p1V1 p2V2 ) закон Бойля-Мариотта.
• Кривая, изображающая зависимость между
величинами р и V, характеризующими свойства
вещества при постоянной температуре,
называется изотермой.
Роберт Бойль
(1627 – 1691)
Эдм Мариотт
(1620 – 1684)
26.
4. Изотермический, изохорный иизобарный процессы
• Изобарный процесс ( p const ) VT const
V1 T1
V2 T2
закон Гей-Люссака.
Жозеф Луи
Гей-Люссак
(1778 – 1850)
27.
4. Изотермический, изохорный иизобарный процессы
p
• Изохорный процесс (V const ) const
T
p1 T1
закон Шарля.
p2 T2
Жак Александр
Цезар Шарль
(1746 – 1823)
28.
4. Изотермический, изохорный иизобарный процессы
• Закон Авогадро: моли любых газов при
одинаковых температуре и давлении
занимают одинаковые объемы.
• При нормальных условиях этот объем
равен:
22,41 10 м / моль
3
p 1,0133 10 Па
5
3
T 273,16 К
29.
4. Изотермический, изохорный иизобарный процессы
• Закон Дальтона: давление смеси
идеальных газов равно сумме парциальных
давлений p1, p2 ,..., рn входящих в нее газов:
p p1 p2 ... pn
• Парциальное давление давление,
которое производил бы газ, входящий в
состав газовой смеси, если бы он один
занимал объем, равный объему смеси при
той же температуре.
30.
5. Скорость молекул газа.Распределение Максвелла
• Доля всех молекул dN/N в объеме газа,
обладающих скоростями в диапазоне от
некоторой υ до ϑ+dϑ является функцией
скорости ϑ :
3 2
4 m0
2 m 2 ( 2 kT )
f ( )
e
2kT
0
• и пропорциональна интервалу скоростей dϑ
dN
f ( )d
N
31.
5. Скорость молекул газа.Распределение Максвелла
• Условие нормировки:
f ( )d 1
0
Функция распределения
Максвелла
Джеймс Клерк
Максвелл
(1831 – 1879)
32.
5. Скорость молекул газа.Распределение Максвелла
• Наивероятнейшая скорость:
2kT
2 RT
н
m0
M
• Среднеарифметическая скорость:
8kT
8RT
m0
M
33.
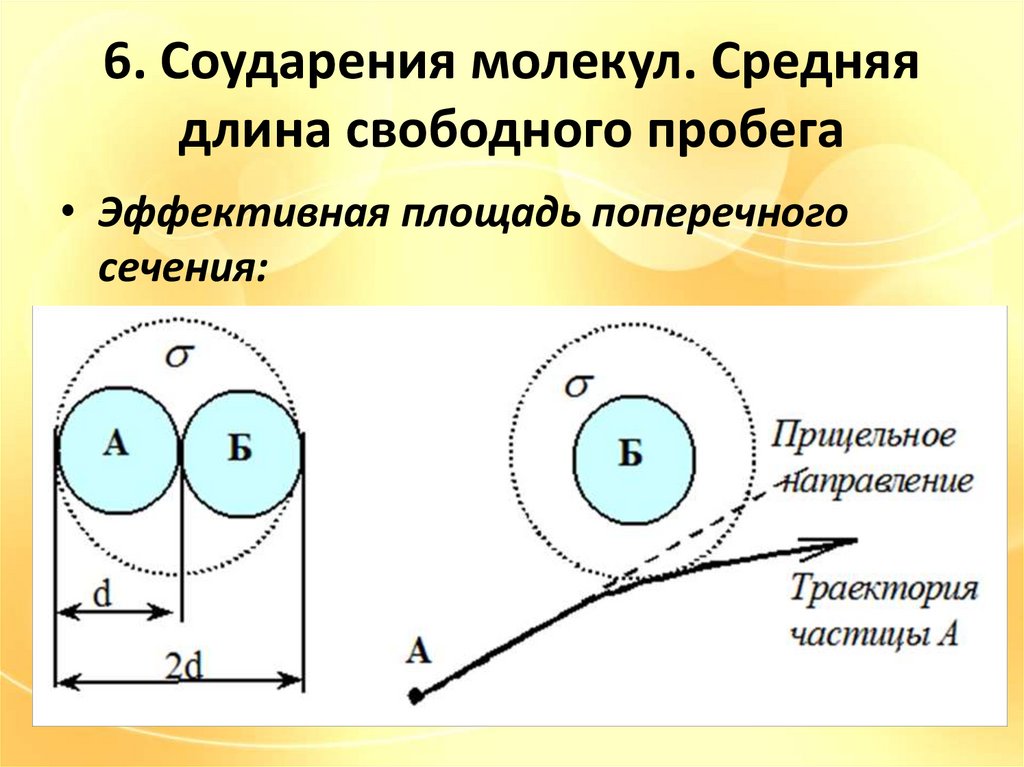
6. Соударения молекул. Средняядлина свободного пробега
• Эффективная площадь поперечного
сечения:
34.
6. Соударения молекул. Средняядлина свободного пробега
• Расстояние, которое проходит молекула
между двумя последовательными
соударениями называется длиной
свободного пробега.
• Средняя длина свободного пробега:
t
l
z t
z
• где среднеарифметическая
скорость, z среднее число соударений
в единицу времени.
35.
6. Соударения молекул. Средняядлина свободного пробега
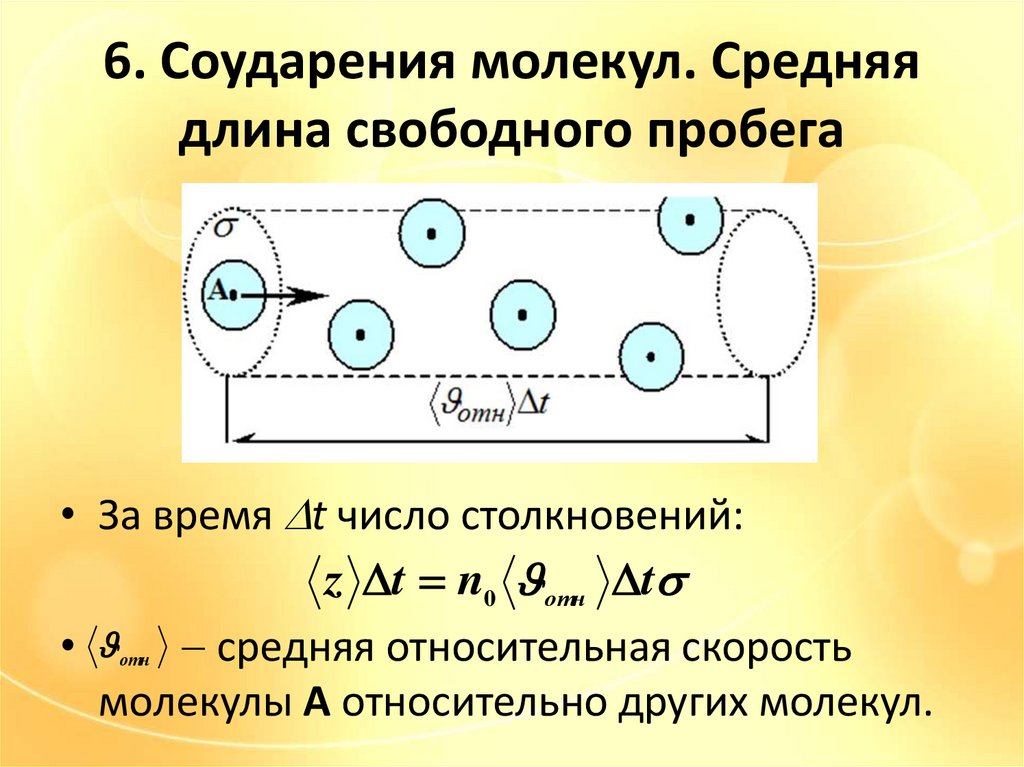
• За время t число столкновений:
z t n0 отн t
• средняя относительная скорость
молекулы А относительно других молекул.
отн
36.
6. Соударения молекул. Средняядлина свободного пробега
• При максвелловском распределении
скоростей:
отн 2
z 2 n0
• Длина свободного пробега:
l
1
2 n0
1
2
2 d n0
37.
7. Явления переноса• К явлениям переноса относятся:
теплопроводность (обусловлена переносом
энергии),
диффузия (обусловлена переносом массы),
внутреннее трение (обусловлено
переносом импульса).
38.
7. Явления переноса• Процессы, связанные со стремлением
системы достигнуть равновесного
состояния, называются процессами или
явлениями переноса.
• Время перехода от неравновесного
состояния к равновесному называют
временем релаксации.
39.
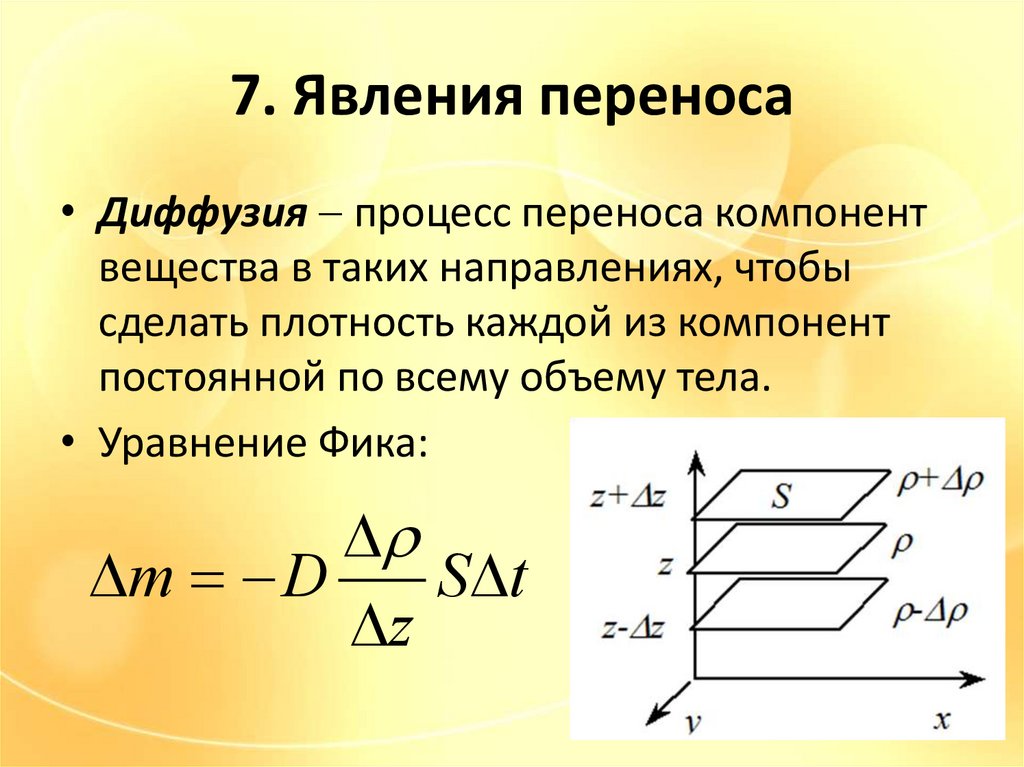
7. Явления переноса• Диффузия процесс переноса компонент
вещества в таких направлениях, чтобы
сделать плотность каждой из компонент
постоянной по всему объему тела.
• Уравнение Фика:
m D
S t
z
40.
7. Явления переноса• Из кинетической теории газов следует:
1
D
3
l
• Вязкость явление возникновения трения
в газах и жидкостях в процессе обмена
импульсом упорядоченного движения
между различными слоями.
41.
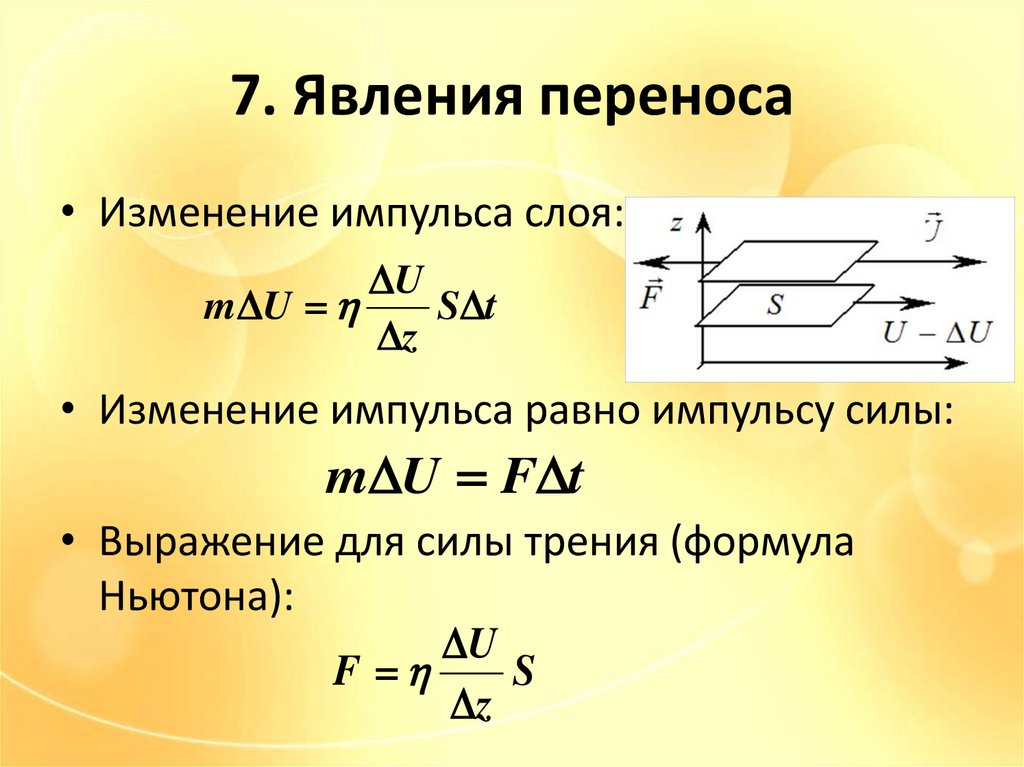
7. Явления переноса• Изменение импульса слоя:
U
m U
S t
z
• Изменение импульса равно импульсу силы:
m U F t
• Выражение для силы трения (формула
Ньютона):
U
F
S
z
42.
7. Явления переноса• Коэффициент вязкости:
1
l
3
• Теплопроводность движение теплоты в
таких направлениях, чтобы сделать
температуру всех частей системы
одинаковой.
43.
7. Явления переноса• Перенос теплоты описывается уравнением
Фурье:
T
Q
S t
z
• Коэффициент теплопроводности:
1
1
n0 k l l CV
6
3





































 physics
physics








