Similar presentations:
Элементы теории вероятностей
1.
Элементы теориивероятностей
2.
Теория вероятностей – это математическая наука, изучающаязакономерности случайных явлений.
Случайное явление – это явление с неопределенным исходом,
происходящее при неоднократном воспроизведении
определенного комплекса условий.
Стоит отметить, что в природе, технике и экономике в каждом
явлении присутствует случайность: в спросе на товар, в погодных
условиях и т.д.
3.
СобытиеОпределение:
Событием в теории вероятностей называется всякий факт,
который может произойти в результате некоторого испытания.
Наблюдаемые нами события можно подразделить на
следующие три вида: достоверные, невозможные, случайные.
4.
Событие достоверное, если при всех испытанияхрассматриваемое событие всегда наступает. Например, мама
старше всех своих детей.
Событие невозможное, если при всех испытаниях событие
никогда не наступает. Например, ребенок старше своих родителей.
Событие случайное, если в результате испытания событие может
произойти или не произойти. Например, выигрываем на
купленный билет лотереи.
5.
6.
7.
8.
9.
10.
11.
Пространством элементарных исходов Ω называется множествовсех взаимно исключающихся исходов испытания. Те исходы, при
которых интересующее нас событие наступает, назовем
благоприятствующими этому событию.
События называются равновозможными, если в результате
испытания ни одно из этих событий не является объективно более
возможным.
События называются несовместными, если наступление одного
из них исключает наступление любого другого. Два события
называются совместными, если появление одного из них не
исключает появления другого в одном и том же испытании.
12.
Вероятность13.
14.
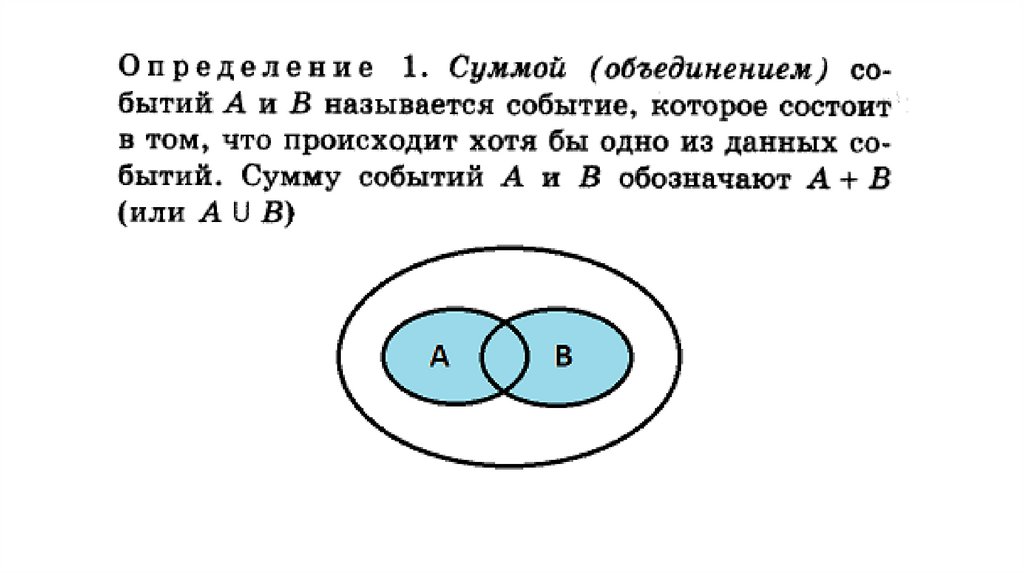
Сложение вероятностейВероятность суммы двух несовместных событий равно сумме
вероятностей этих событий, т.е.
Сумма вероятностей противоположных событий равна единице,
т.е.
15.
16.
Умножение вероятностейСобытия А и В называют независимыми, если выполняется
равенство
17.
18.
19.
Статистическая вероятностьОтносительной частотой события А в данной серии испытания
называют отношение числа испытаний М, в которых это событие
произошло, к числу всех проведённых испытаний N. При этом
число М называют частотой события А.
20.
Статистической вероятностью называют число, около которогоколеблется относительная частота события при большом числе
испытаний.
21.
ДЗ1128, 1141, 1149, 1157.




















 mathematics
mathematics