Similar presentations:
Понятие о концентрации напряжений. Усилия и напряжения от собственного веса стержня
1.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Строительной механики
Тема 3
Понятие о концентрации напряжений
Усилия и напряжения от собственного веса стержня
Статически неопределимые задачи при растяжении-сжатии
Авторы:
к.т.н., Войтко Александр Михайлович
к.т.н., Алейник Вадим Иванович
1
2.
Тема 2. Растяжение и сжатие2.6. Понятие о концентрации напряжений
Концентрация напряжений – это резкое повышение напряжений
в ослабленном сечении стержня, в местах резкого его изменения
Напряжения в зоне концентрации называются
местными напряжениями
Показатель местных напряжений:
коэффициент концентрации напряжений
м
,
ср
(3.1)
σ м максимальные напряжения в зоне концентрации
σ ср средние напряжения в неослабленном сечении
2
3.
32
Понижение концентрации напряжений
3
4.
2.7. Усилия и напряжения от собственного веса стержня‒ объемный вес материала;
q A ‒ вес единицы длины.
Продольная сила:
N x qx Ax .
(3.2)
4
5.
Нормальные напряжения:x
N x
A
Ax
x.
A
(3.3)
1. Усилия и напряжения изменяются по линейному закону.
2. Напряжения от собственного веса не зависят от площади сечения.
Абсолютная деформация бесконечно малого участка:
d l
N x dx
EA
.
(3.4)
Полная деформация участка от x до l:
l
l
x
N x
EA
l
dx
x
x
E
Полная деформация всего стержня:
dx
x
2 l
E 2 x
lmax
2E
l2
2E
.
2
2
l
x
.
(3.5)
(3.6)
5
6.
2.7.2. Стержень равного сопротивления при растяжении-сжатииНапряжения в любом сечении:
F
.
A0
(3.7)
1. Изменение продольной силы равно весу участка:
dN x A x dx .
(3.8)
2. Продольная сила через постоянные напряжения:
N x A x ,
Приравняем правые части (3.8) и (3.9):
dN x dA x .
(3.9)
A x dx dA x .
(3.10)
6
7.
Разделим переменные в (3.10):Интеграл (3.11):
x
dA
;
A
0
ln A0C .
(3.11)
x
x
ln A ln C , или
ln AC ,
при x 0 A A0 .
Граничное условие:
С в (3.12):
dA
dx
.
A x
Подставим в (3.12):
1
A0C 1 , или C .
A0
x
A
ln ,
A0
Потенцируем:
(3.12)
(3.13)
e
x
A
.
A0
(3.14)
7
8.
Закон изменения площади сечения:x
A A0e .
(3.15)
Чтобы напряжения по высоте стержня не менялись,
площадь сечения должна изменяться по экспоненте.
Стержень, напряжения в любом сечении которого одинаковы,
называется стержнем равного сопротивления
8
9.
2.8. Статически неопределимые задачи при растяжении-сжатииСтатически неопределимая расчетная схема – система, в которой
все реакции и усилия не могут быть определены только из условий
равновесия
2.8.1. Статически неопределимые упругие задачи
Разрешающие уравнения статически неопределимой задачи:
1) Уравнения равновесия (статические)
2) Условия совместности деформаций (геометрические)
3) Физические уравнения (закон Гука)
Особенность статически неопределимых систем:
усилия и напряжения возникают не только от
силовых нагрузок, но и от начальных деформаций
(температурные изменения, неточность изготовления)
9
10.
Пример 2.1. К стальному стержню, защемлённому двумя концами, приложена сила 100 кН.ЕА = const. Определить реакции опор.
1. Уравнение равновесия:
2. Условие совместности деформаций:
3. Закон Гука:
X 0 ; 100 R R 0 .
(3.16)
l1 l2 .
(3.17)
1
2
R1l1
R2l2
l1
, l2
.
EA
EA
(3.18)
Решение системы: подставим (3.18) в (3.17):
10
11.
R1l1 R2l2,
EA EA
l2
30
R1 R2 R2 1,5R2 .
l1
20
отсюда:
Подставим (3.20) в (3.16):
(3.20)
R1 R2 100 ; 1,5 R2 R2 100 .
R2 40 кН, R1 60 кН.
Продольные силы:
(3.19)
N1 R1 60 кН.
(3.21)
N 2 R2 40 кН.
11
12.
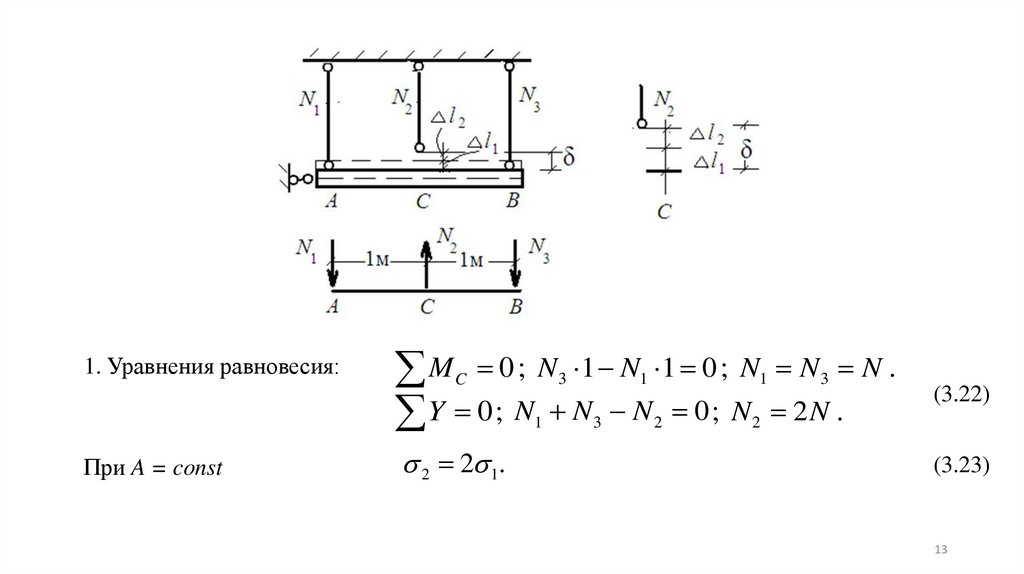
Пример 2.2. Учет неточности изготовления элементов конструкций.Жесткий брус на трех упругих опорах (стержнях). Площади A = const.
Стержень С короче проектной длины на δ = 1,5 мм. Определить напряжения в стержнях. Е = 2∙105 МПа (20000 кН/см2).
При сборке конструкции стержень С удлинится на Δl2,
стержни A и B укорачиваются на Δl1 (симметрия):
12
13.
1. Уравнения равновесия:M 0 ; N 1 N 1 0 ; N N N .
Y 0 ; N N N 0 ; N 2 N .
(3.22)
2 2 1.
(3.23)
3
C
1
При A = const
1
3
1
2
3
2
13
14.
l1 l2 .2. Условие совместности деформаций:
3. С учетом закона Гука:
1 2 1
1l 2l
E
E
l
E
; 3 1
. 1 2
E
l
(3.24)
E
l
;
.
(3.25)
Результат:
0,15 20000
1
3,33 кН/см2 = 33,3 МПа (сжатие).
300 3
2 2 33,3 66,7 МПа (растяжение).
14
15.
Пример 2.3. Влияние изменения температуры на напряжения.а) . Стержень, закрепленный жестко с двух концов, находился при температуре
t1 и был нагрет до температуры t2 > t1. Длина стержня возрастает при температурном расширении. Реакции опор стержня вызывают сжатие в стержне.
б) . Стержень находился при температуре t1 и был охлажден до температуры t2 < t1.
Длина стержня уменьшается при понижении температуры. Реакции опор стержня
вызывают растягивающие усилия.
15
16.
Случай а) определение температурных напряжений:1. Уравнение равновесия:
RA RB 0.
(3.26)
lt lR .
(3.27)
lt tl ,
температурная деформация стержня без правой опоры;
по закону линейного температурного расширения
(3.28)
RB l
l R
.
EA
деформация стержня, вызванная реакцией правой опоры;
определяется по закону Гука.
(3.29)
2. Условие совместности деформаций:
3. Физические соотношения:
16
17.
Подставим (3.28) и (3.29) в (3.27):RB l
tl
.
EA
Отсюда:
Температурные напряжения:
При :
t1 5 , t2 40 ,
(3.30)
RB
t
E t .
A
1, 2 10 5 1/град, E 2 105 МПа,
t 2 105 1, 2 10 5 40 5 84 МПа.
(3.31)
получим
(сжатие)
Усилия и напряжения в статически неопределимых системах при расчете
на силовую нагрузку зависят от соотношения жесткостей их элементов.
При расчете на температурные и монтажные воздействия усилия прямо
зависят от значений жесткостей.
17
18.
2.8.2. Расчет статически неопределимых системпо предельному пластическому состоянию
Предельным
пластическим
состоянием
конструкции
называют такое состояние, при котором система становится
изменяемой за счет развития пластических деформаций, то
есть превращается в механизм.
Расчет по упругой стадии:
условие прочности для наиболее
напряженного элемента
max или max R .
FT
F Fд
,
n
где FT ‒ предельная нагрузка
Расчет по предельному пластическому
состоянию: условие прочности для
всей конструкции
(3.32)
(3.33)
18
19.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
к.т.н., Алейник Вадим Иванович
tehmeh@spbgasu.ru
19


















 mechanics
mechanics








