Т3_2 КХФ

1.

Академия ФСО России
Кафедра № 11
семинар по учебной дисциплине
«Методы и средства криптографической
защиты информации»

Тема 3. Принципы построения несимметричных
криптосистем
Занятие 2. Функции хеширования
Цель занятия:
1) изучение основных понятий и порядка формирования КХФ;
2) формирование способностей использовать методы и средства криптографической
защиты информации при решении задач профессиональной деятельности.
Учебные вопросы:
Вопрос 1. Элементы теории чисел в криптографии.
Вопрос 2. Свойства криптографических хеш-функций.
Вопрос 3. Способы построения криптографических хеш-функций.
2/20

3.

Вопрос 1. Элементы теории чисел в криптографии
Основные понятия и определения модулярной арифметики:
– позиционные и непозиционные (СОК) системы счисления;
– простые числа и взаимно простые числа;
– сравнимые по модулю числа.
Основные теоремы, используемые в модулярной арифметике:
– теорема Эйлера; – малая теорема Ферма; – китайская теорема об остатках.
Способы нахождения обратных величин: поочередная проверка, с помощью
функции Эйлера, расширенным алгоритмом Евклида.
Основные понятия и определения:
– асимметричная криптосистема;
– однонаправленная функция (односторонняя, вычислительно необратимая);
– примитивный элемент.
Примеры однонаправленных функций в криптографии.
3/20

4.

Написание слова
« х е ш » – соответствует современным нормам русского языка;
« х э ш » – исторически сложившееся написание.
4/20

5.

Вопрос 2. Свойства криптографических хеш-функций
В общем случае хеш-функцией является произвольная функция h, которая
имеет, как минимум, два свойства:
•сжатие: функция h отображает входную дискретную последовательность
x произвольного конечного размера в выходную последовательность h(x)
фиксированной длины n;
•вычислительная простота определения значения хеш-функции: для
заданной функции h и входной последовательности x легко вычислить
значение h(x).
Применение хеш-функций:
1) для идентификации (построение ассоциативных
массивов, создание уникальных идентификаторов);
2) для ускоренного поиска данных
(проверка информации на идентичность
оригиналу без использования оригинала,
поиск дубликатов, …);
3) для контроля целостности данных при их хранении и/или передаче.
5/20

6.

Для множества информационных сообщений Х хеш-функция h
отображает любое сообщение x в его хеш-код:
H = h(x).
Если различные сообщения x ≠ x' отображаются в один и тот же
хеш-код h(x) = h(x'), то данная хеш-функция допускает коллизии
сообщений (от лат. Collisio – столкновение).
Индекс хеширования I(h, x) функции h на множестве сообщений X:
1 N 2
I (h, X ) ti 1
X i 1
где ti – количество сообщений, отображающихся в конкретный хешкод (i = 1, 2, …, N);
N – количество различных хеш-кодов (N ≤ 2n);
n – двоичная длина хеш-кодов
Если I(h, X) = 0 – коллизий нет, хеш-функция совершенная.
6/20

7.

Криптографические хеш-функции (КХФ)
Криптографической хеш-функцией (термин введен Р. Мерклом в 1979
г.) называется всякая хеш-функция, являющаяся криптостойкой, т. е.
обладающая дополнительными свойствами, выполняемыми при
условии, что злоумышленник знает описание функции и статистические
характеристики множества сообщений X и множества хеш-кодов:
– стойкость к вычислению прообраза (необратимость): для почти всех
значений хеш-функции H вычислительно невозможно отыскать любой
прообраз x, который хешируется к заданному значению H = h(x);
– стойкость к коллизиям первого рода: для заданного прообраза x
вычислительно невозможно отыскать любой второй прообраз x', не
равный x, который хешируется в такое же значение хеш-функции h(x) =
h(x');
– стойкость к коллизиям второго рода: вычислительно невозможно
отыскать любые два различных прообраза x и x', которые хешируются в
одинаковое значение хеш-функции, т. е. h(x) = h(x').
Криптографическим хеш-функциям присущ лавинный эффект.
7/20

8.

Области применения КХФ
Проверка целостности сообщений и файлов:
– при хранении и передачи данных;
– Torrent, Git, P2P File Sharing и др.
Генерация и проверка цифровой подписи:
– практически все схемы ЦП используют КХФ.
Проверка логинов и паролей пользователей ИС:
– хранение в открытом виде – серьезное нарушение безопасности
(компрометация);
– добавление «соли» (Salt) – случайного несекретного значения, которое
может быть сохранено вместе с хеш-кодом пароля.
Проверка работоспособности (Proof-of-Work):
– система предотвращения злоупотребления услугами (защита от атак типа
«отказ в обслуживании», рассылки спама по сети и т.п.), требующая
некоторой работы от лица, запрашивающего услуги (время обработки);
– Blockchain-сети (подтверждение транзакций, майнинг и др.).
Формирование ПСП (синхропосылки, гаммы и др.)
8/20

9.

Выводы по второму учебному вопросу
Хеш-функции (определение).
Свойства (раскрыть смысл): сжатие
вычислительная простота
Области применения (перечислить).
Криптографическая хеш-функция (дать определение, назвать и
пояснить её дополнительные свойства).
9/20

10.

Вопрос 3. Способы построения криптографических
хеш-функций
Криптографическая хеш-функция с секретным ключом (ХФСК) – если в
процессе хеширования сообщений используется секретный ключ k:
H = h(x, k).
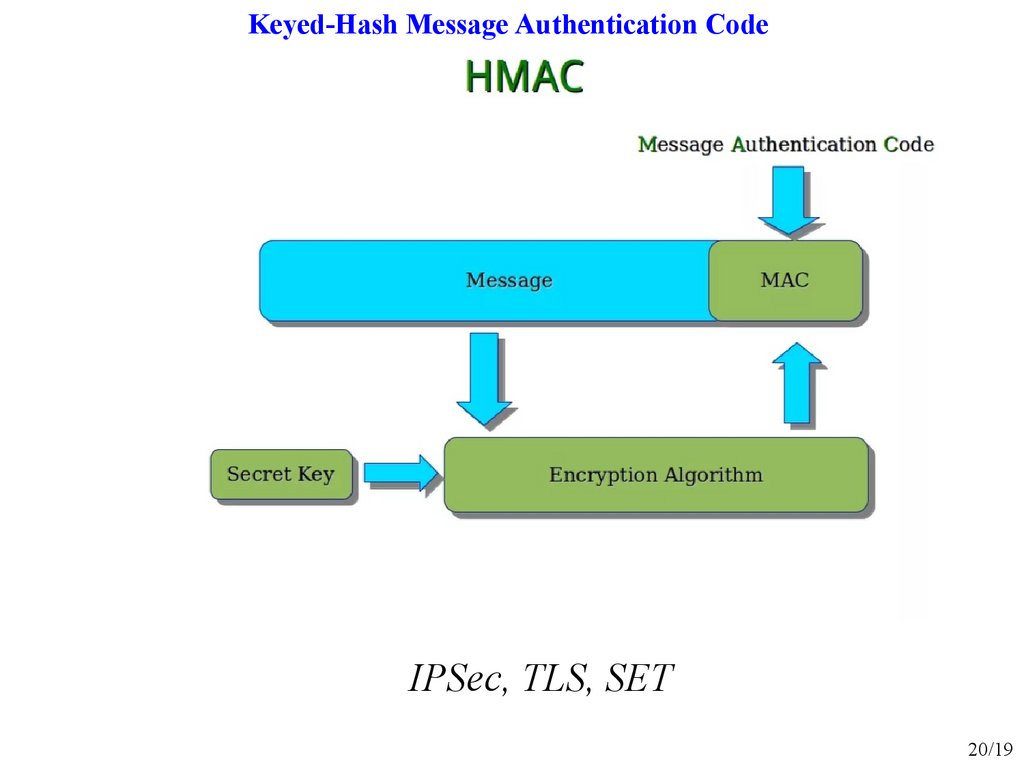
Например, коды аутентичности сообщений (КАС) – MAC.
Бесключевые криптографические хеш-функции (БКХФ) – криптографические
хеш-функции, не использующие секретного ключа для хеширования
сообщений:
H = h(x).
Например, коды обнаружения ошибок – MDC.
Сообщение x
Ключ k
(соль)
Сообщение x
Хеширование
h(x)
Хеширование
h(x, k)
Хеш-код H
Хеш-код H
БКХФ
ХФСК
10/20

11.

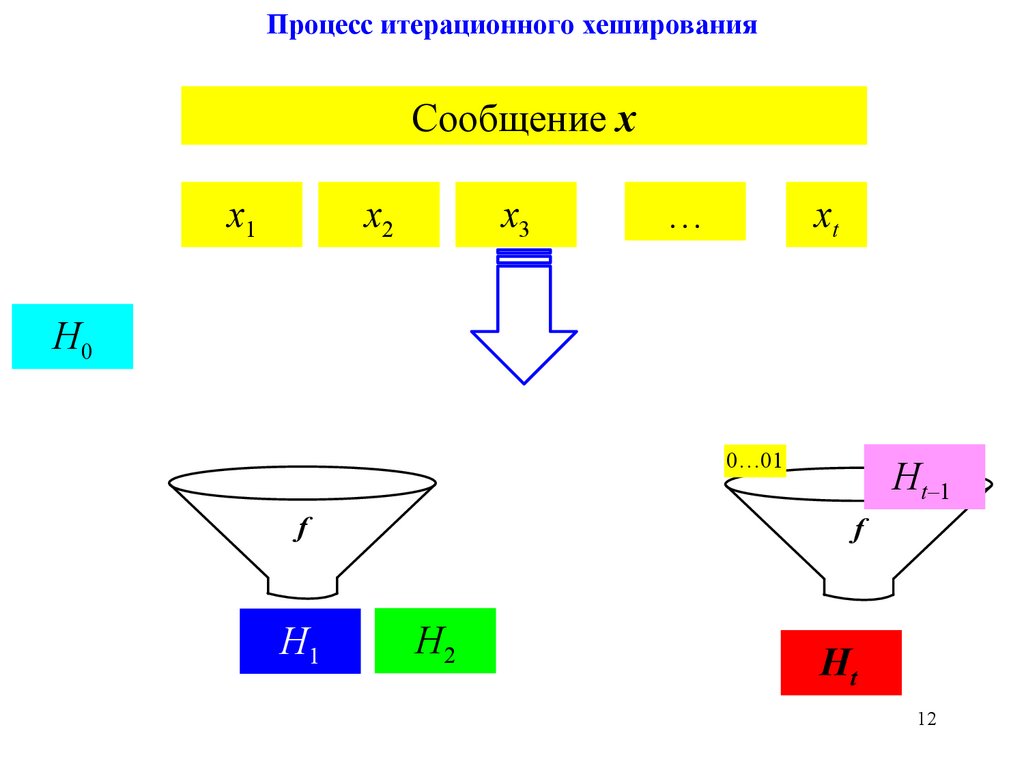
Итеративное хеширование
Хешируемое сообщение x делится на t блоков от x1 до xt длиной по n бит.
Если длина сообщения не кратна длине блока, то сообщение дополняется до
длины, кратной длине блока.
Для инициализации процесса итеративного хеширования необходимо
задать стартовый вектор хеширования Н0 длиной n бит.
Хеширование сообщения x:
x = (x1, ..., xi, ..., xt),
i = 1, 2,..., t;
Hi = f (xi, Нi 1),
h(x) = Ht,
где Hi значение хеш-кода функции на i-й итерации,
f – шаговая функция хеширования,
h(x) – значение хеш-кода всего сообщения x.
11/20

12.

Процесс итерационного хеширования
Сообщение x
x1
x2
x3
…
xt
H0
0…01
f
H1
Ht–1
f
H2
Ht
12

13.

Структура Меркла–Дамгарда
Усиление Меркла–Дамгарда
Сообщение x
x1
Стартовый
вектор H0
f
...
x2
H1
f
H2
...
Длина
сообщения x
xt Доп.
Ht–1
f
Ht
f
H
Примеры хеш-функций: MD5, SHA-1, SHA-2, ГОСТ Р 34.11–2012 и др.
Структура Меркла–Дамгарда
Структура Дэвиса–Мейера
Структура Матиса–Мейера–Осеаса
Ральф Чарльз Меркл
02.02.1952
Структура Миагучи–Пренеля
Иван Бьерре Дамгард
17.04.1956
13/20

14.

Структура Дэвиса–Мейера
(Метод Уинтерница)
Hi – 1
xi
ki
Ek
Примеры КХФ:
MD5
SHA-256
BLAKE
ГОСТ Р 34.11–94
Hi
Хешируемое сообщение x разбивается на равные по длине блоки xi, на которых
как на ключах последовательно зашифровываются предыдущие значения
хеш-функции Hi 1.
На первом блоке сообщения x1 зашифровывается стартовый вектор H0.
Hi = Exi(Hi 1) Hi 1
14/20

15.

Структура Матиса–Мейера–Осеаса
xi
Hi – 1
g
ki – 1
Ek
Пример КХФ:
Skein
Hi
Для получения следующего значения Hi блок исходного сообщения xi
зашифровывается на предыдущем значении хеш-функции Hi 1 и складывается
по модулю 2 с тем же блоком исходного сообщения xi.
Функция g необходима для преобразования хеш-кода, когда блочный шифр
имеет различные размеры блока сообщения и ключа.
Hi = Eg(Hi 1)(xi) xi
15/20

16.

Структура Миагучи–Пренеля
xi
Hi – 1
g
ki – 1
Ek
Примеры КХФ:
Whirlpool
«Стрибог»
Барт Пренель
15.09.1963
Hi
Каждый блок исходного сообщения xi зашифровывается на предыдущем
значении хеш-функции Hi 1.
Затем выполняется операция XOR зашифрованного текста с тем же блоком
исходного сообщения xi и с предыдущим значением хеш-функции Hi 1 для
получения следующего значения Hi.
Hi = Eg(Hi 1)(xi) Hi 1 xi
16/20

17.

Структура Sponge-конструкции
Традиционные структуры хеш-функций основаны на использовании
псевдослучайной функция сжатия (PRF – Pseudo Random Function),
отображающей блоки исходного сообщения произвольной длины в хеш-код,
дополняя и сцепляя их между собой.
Существуют КХФ, которые строятся на основе псевдослучайных перестановок
(PRP – Pseudo Random Permutation) – Sponge-конструкции (губки).
Пример: SHA-3 (на основе хеш-функции Keccak), JH, Luffa.
Сообщение x
x1
r
c
0
0
...
x2
Sr
f
Sc
f
...
xt Доп.
H1
Sr
Sc
H2
Sr
f
Абсорбция
где f – многораудовая бесключевая PRP-функция;
r и с – нулевые векторы инициализации
Sc
Sr
f
Sc
f
...
Сжатие
17/20

18.

Известны устойчивые к коллизиям криптографические хеш-функции,
основанные на модулярной арифметике (например, MASH-1 и MASH-2).
Пример КХФ, стойкость которой основана на вычислительной сложности
задачи факторизации большого составного числа:
Hi = f ((xi + Hi 1)2 mod n) + xi,
где n большое составное число (n = p·q).
Недостаток: низкая скорость RSA-шифрования (на 2–3 порядка ниже БШ).
Хеш-функции
общего назначения
Adler-32, CRC, FNV, Murmur2, PJW-32,
TTH, Jenkins hash
HAVAL, Keccak, LM-хеш, MD2, MD4,
MD5, MD6, N-Hash, RIPEMD-128,
RIPEMD-160, RIPEMD-256, SM3,
Криптографические RIPEMD-320, SHA-1, SHA-2, SHA-3,
хеш-функции
Skein, Snefru, Tiger, Whirlpool,
ГОСТ Р 34.11–94, ГОСТ Р 34.11–2012
ISO/IEC
10118-3:2018
18/20

19.

Выводы по третьему учебному вопросу
Виды КХФ
Криптографическая хеш-функция
с секретным ключом (MAC)
Бесключевые криптографические
хеш-функции (MDC)
В основе вычисления хеш-кода лежит итеративное хеширование
Методы (способы) хеширования
Структура Меркла-Дамгарда
Дэвиса–Мейера
Матиса–Мейера–Осеаса
Миагучи–Пренеля
Sponge-конструкция
19/20

20.

Keyed-Hash Message Authentication Code
IPSec, TLS, SET
20/19

21.

English Русский Rules