Similar presentations:
Применение эвристических алгоритмов к задачам поиска максимально нелинейных векторных булевых функций
1.
Применение эвристическихалгоритмов к задачам поиска
максимально нелинейных
векторных булевых функций
Студент: М.Ф. Тагойбекзода
Руководитель: Тонких Артём Петрович
2023
2.
АктуальностьВекторные булевы функции – основа криптосистем.
Свойства векторных булевых функций:
- нелинейность
- сбалансированность
3.
Цель и задачиЦель – получение сбалансированных функций
максимальной нелинейности.
Задачи:
построить и уточнить границы максимальной
нелинейности
найти векторные булевы функции с нелинейностью,
приближающейся к границам максимальной
нелинейности
найти сбалансированные векторные булевы функции
с такой нелинейностью
запрограммировать и сравнить методы достижения
указанной цели
4.
Постановка задачиЗадача без ограничений
Сбалансированная задача
5.
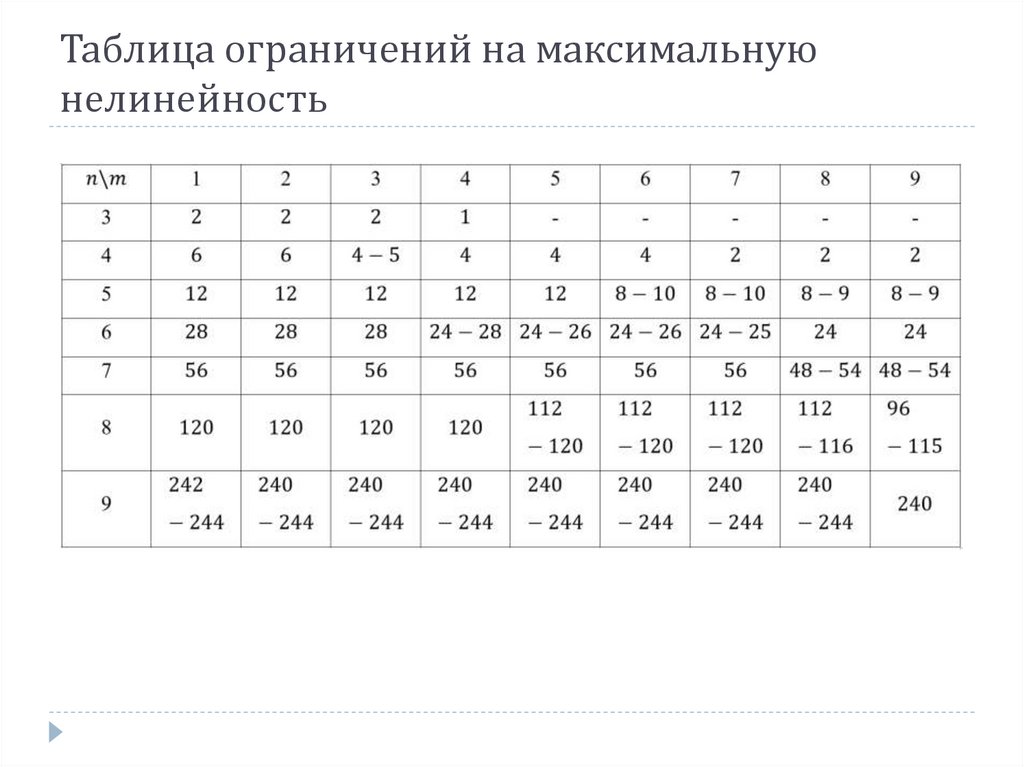
Таблица ограничений на максимальнуюнелинейность
6.
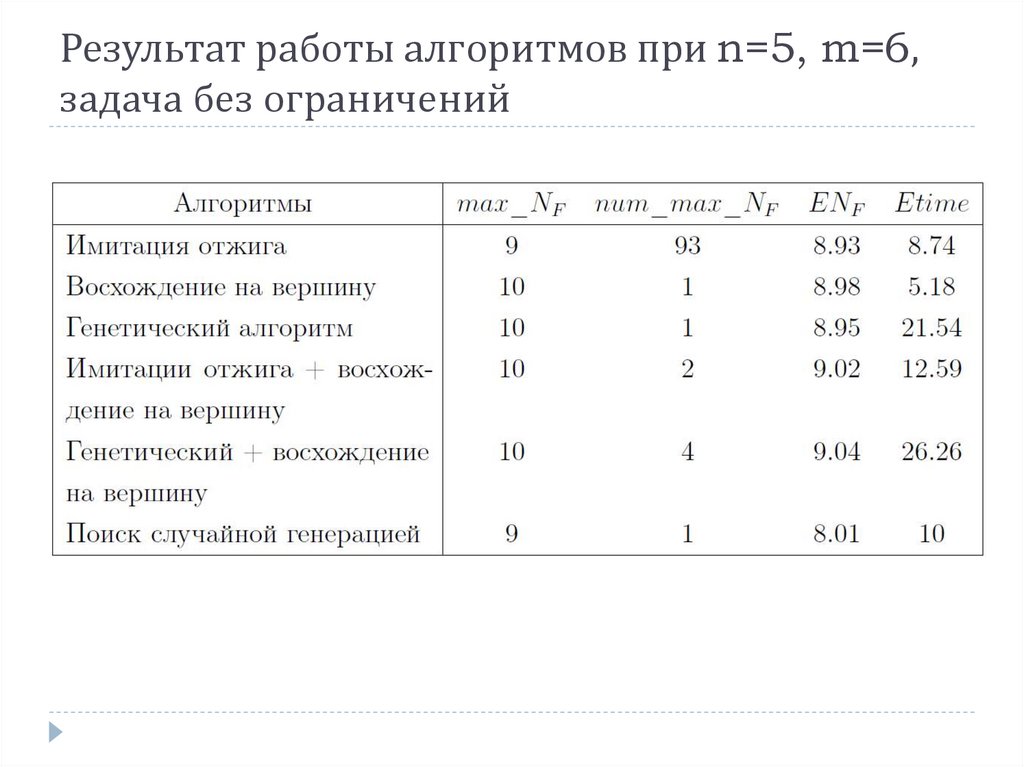
Результат работы алгоритмов при n=5, m=6,задача без ограничений
7.
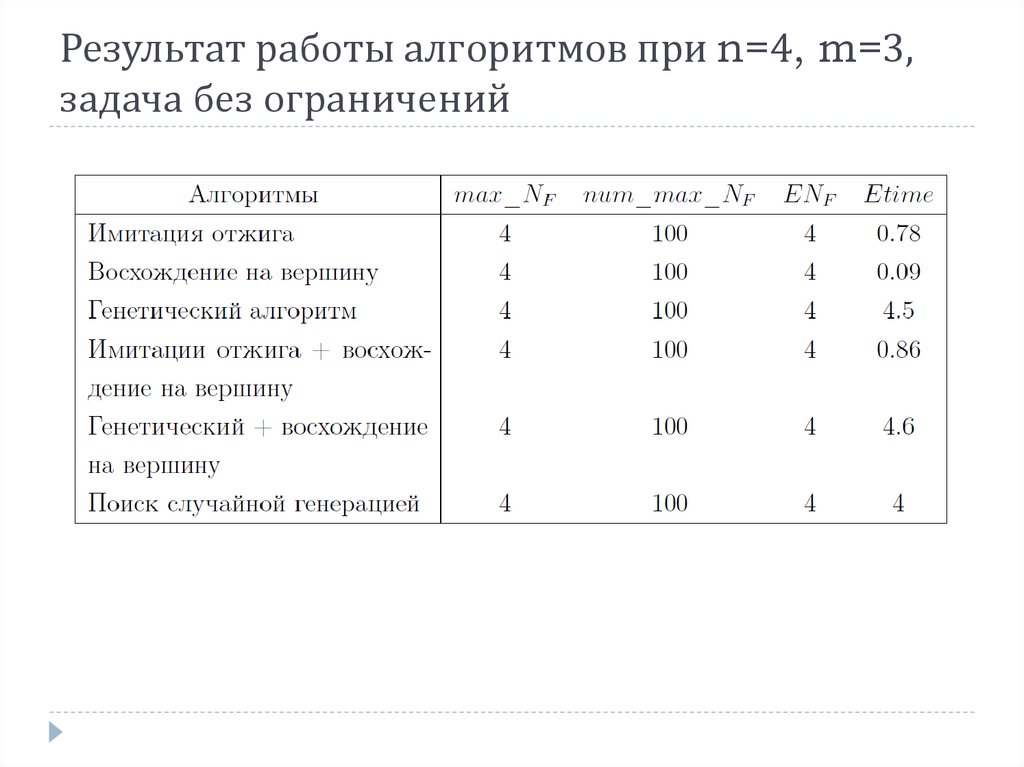
Результат работы алгоритмов при n=4, m=3,задача без ограничений
8.
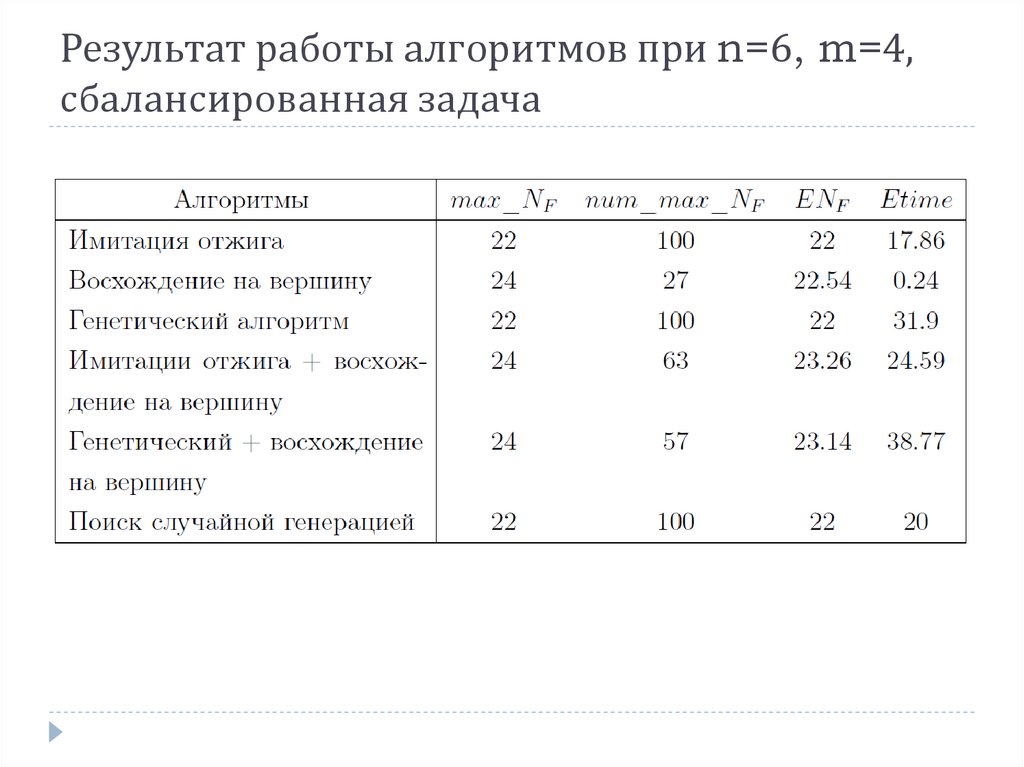
Результат работы алгоритмов при n=6, m=4,сбалансированная задача
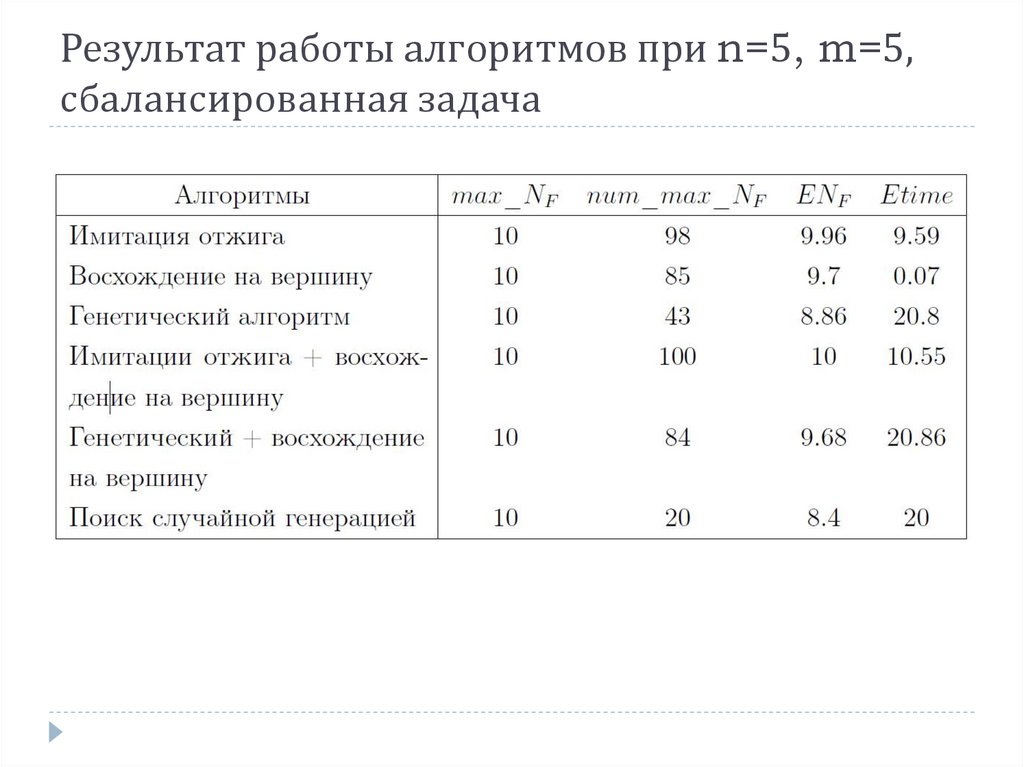
9.
Результат работы алгоритмов при n=5, m=5,сбалансированная задача
10.
ЗаключениеПрименены эвристические алгоритмы и их
комбинации.
Алгоритмы запрограммированы на Java. Применён
генетический алгоритм Matlab.
Предложен и протестирован набор модификаций.
Рассмотрены теоретические границы максимальной
нелинейности.
Для случаев n = 5, m = 6 и n = 8, m = 9 уточнены
границы максимальной нелинейности снизу.
Собрана и проанализирована статистика.





 mathematics
mathematics








