Карта карно (1)

1.

Карты Карно

2.

Карта Карно — графический способ минимизации булевых функций,
обеспечивающий относительную простоту работы с большими
выражениями. Представляет собой операции попарного неполного
склеивания и элементарного поглощения. Карты Карно
рассматриваются как перестроенная соответствующим образом
таблица истинности функции.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и
усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и
были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности
и упорядочиваются с помощью кода Грея, в котором каждое
следующее число отличается от предыдущего только одним разрядом.
Каждой строке таблицы истинности логической функции соответствует
одна клетка карты Карно.

3.

Карты Карно
--для
для трех
двух
четырех
- для
переменных
переменных
пяти
переменных
переменных

4.

Карты Карно логических функций 2-х, 3-х и 4-х переменных – 2-x
мерные, т.е. представимы на плоскости.
Карты Карно логических функций 5-ти и 6-ти переменных 3-х
мерные или пространственные.
Метод применим только для логических функций до 7-ми
переменных.
Свойства карт Карно:
1. Каждой клетке карты Карно соответствует один аргументвектор логической функции.
2. Число соседних клеток к каждой клетке карты Карно равно
числу переменных карты.
3. Аргумент-векторы любых двух соседних клеток карты Карно
являются ближайшими друг к другу аргумент-векторами
(отличаются друг от друга только в одной координате).

5.

Рассмотрим на примере. Пусть задана таблица
истинности:
Составим три отдельные карты для функций
y1, y2, y3.

6.

Заполним карту Карно для функции y1:
0
0
1
0
0
0
1
0
0
1
1
1
1
0
1
1
Четвертая
строка
x1для
=1,
соответственно
Третья
строка
длядля
x1=1,
x2x=1
2=0
Первая
Вторая
строка
xсоответственно
=0,
x =1
=0
11
22

7.

Для дальнейших действий введем понятие «контур». Группы клеток
карты Карно определенных размеров называют контурами.
Для карт Карно, определенных на плоскости, контурами являются
прямоугольники, с допустимыми размерами сторон 2m x 2n, m, n = 0,
1, 2 …
1x1
1x2
1x4
2x1
2x2
2x4
4x1
4x2
4x4
...

8.

Для создания МКНФ выделяются контуры с нулевыми
элементами, для МДНФ – элементы с единичными элементами.
Выделение контуров:
Также, одномогут
из важных
свойств
– «склееность»
границ
карты. Граничные
Возможные
контуры
Контуры
пересекаться,
причем
элементы
должны
правые элементы являются соседними для граничных левых, верхние –
входить в максимально
для нижних.большой контур

9.

Продолжим решение примера. Выделим контуры с единичными
элементами для МДНФ на заполненной карте.
0
0
1
0
0
0
1
0
0
1
1
1
1
0
1
1
Теперь выделим
Выделим
меньшие
максимально
контуры.
большие
Причем,
контуры
учитывая
(они
«склееность»
могут пересекаться)
границ карты.

10.

Последний этап. По постоянным переменным интервалов запишем
элементарные конъюнкции МДНФ по правилу составления СДНФ или
СКНФ по заданной области истинности или ложности.
Постоянные значения x3 прямой,
прямой
Постоянное
Постоянное
Постоянное
значение
значение
значение
x x-4-xинверсный
x- прямой
- прямой
4
y1= x3x4 + x1x3 + x1x2x 4+ x1x2x 4
Постоянные значения x1 – прямой,
x2 Постоянное
– прямой значение
x1 - прямой
Постоянные значения x1 – прямой,
x2 – инверсный
4 3
0
0
1
0
0
0
1
0
0
1
1
1
1
0
1
1

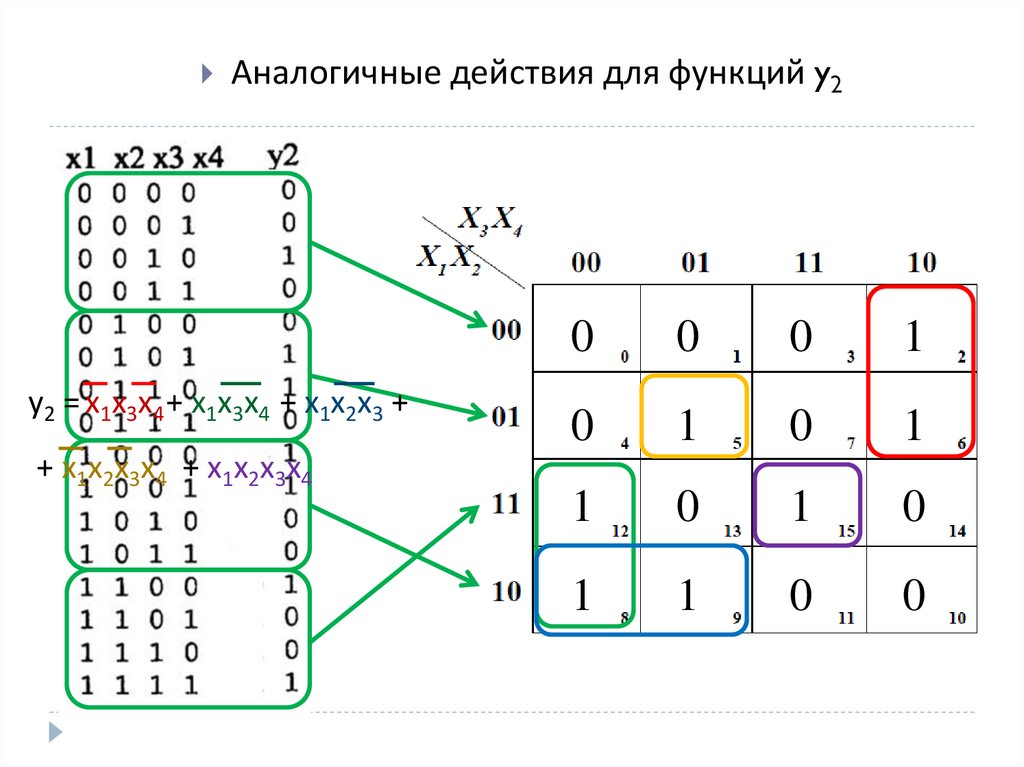
11.

Аналогичные действия для функций y2
y2 = x1x3x4 + x1x3x4 + x1x2x3 +
+ x1x2x3x4 + x1x2x3x4
0
0
0
1
0
1
0
1
1
0
1
0
1
1
0
0

12.

И для функций y3
y3 = x1x2+x2x4
0
1
1
0
0
0
0
0
1
1
1
1
0
1
1
0

13.

Итого, мы привели к МДНФ три функции,
руководствуясь только таблицей истинности и картами
Карно.
y1= x3x4 + x1x3 + x1x2x 4+ x1x2x 4
y2 = x1x3x4 + x1x3x4 + x1x2x3 + x1x2x3x4 + x1x2x3x4
y3 = x1x2+x2x4