1078728 (1)

1.

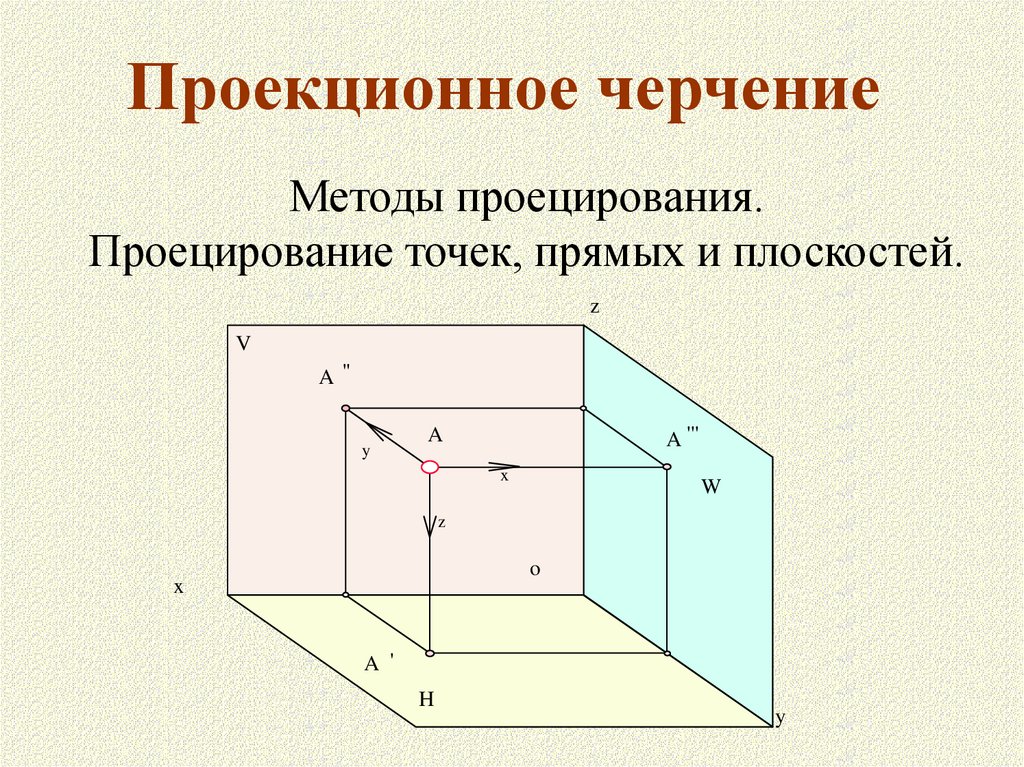
Проекционное черчение
Методы проецирования.
Проецирование точек, прямых и плоскостей.
z
V
A"
y
A '''
A
x
W
z
o
x
A '
H
y

2.

Что называется проекцией предмета на плоскость?
Что такое проецирование?
Как осуществляется процесс построения проекции?
Какие существуют методы проецирования?
Как спроецировать предмет на плоскость?

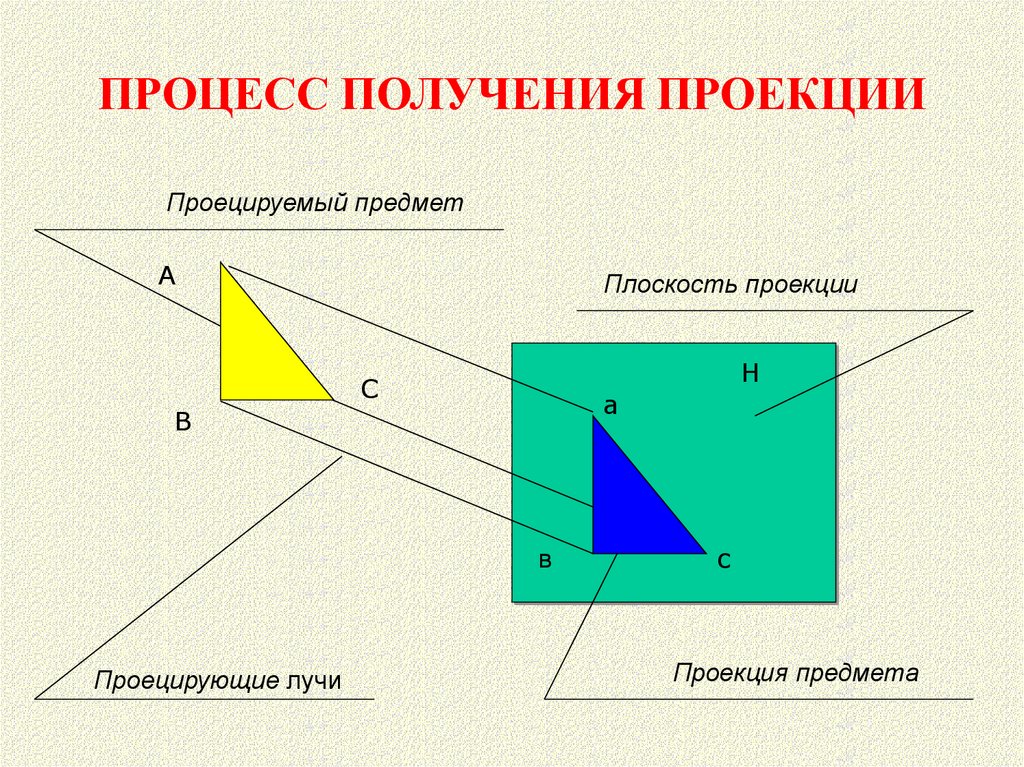
3. ПРОЕКЦИЯ – изображение предмета на плоскости, полученное с помощью проецирующих лучей.

• Проекция - своеобразная тень предмета

4.

ПРОЦЕСС ПОЛУЧЕНИЯ ПРОЕКЦИИ
Проецируемый предмет
A
Плоскость проекции
H
C
a
B
в
Проецирующие лучи
c
Проекция предмета

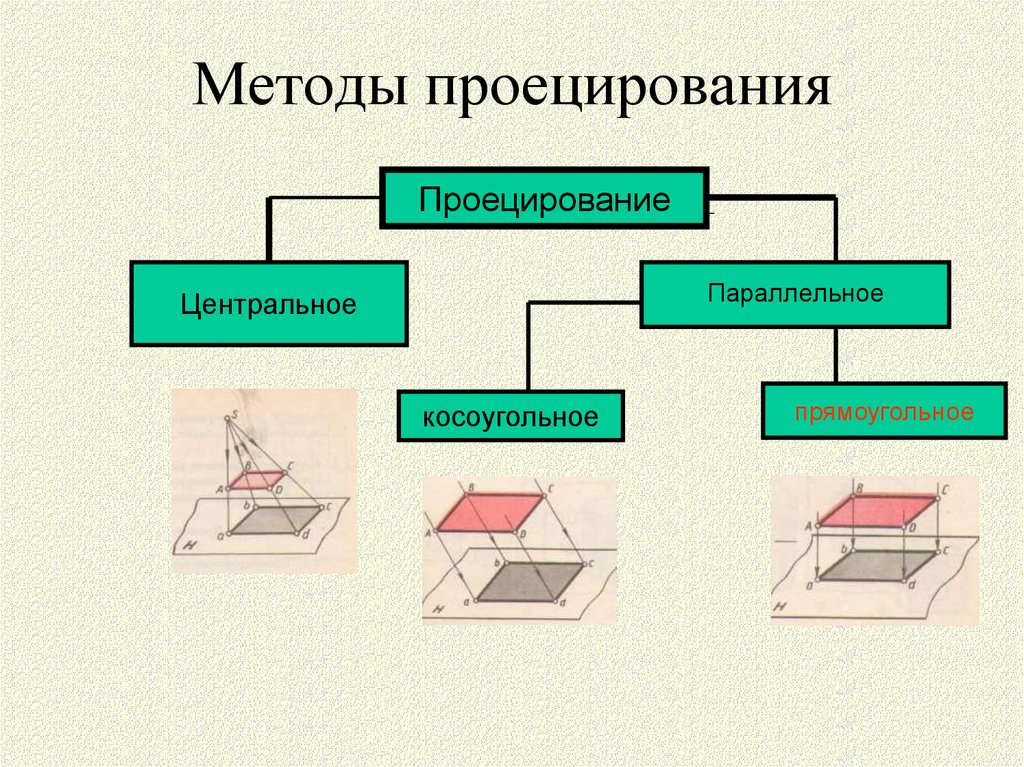
5. Методы проецирования

Проецирование
Параллельное
Центральное
косоугольное
прямоугольное

6.

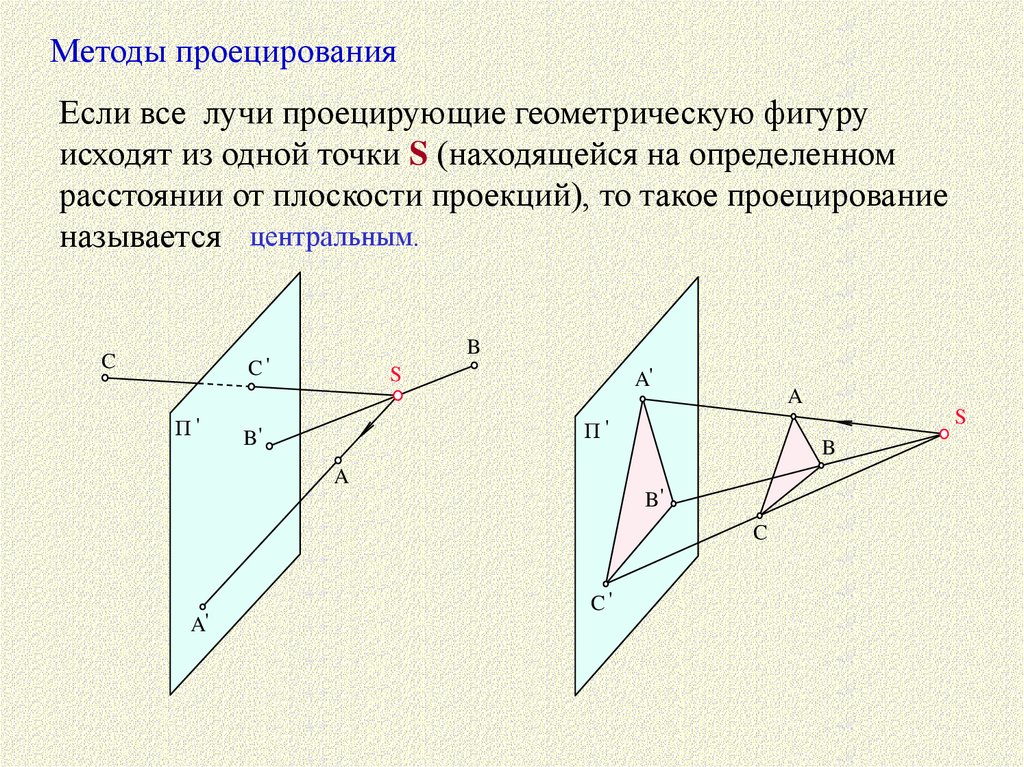
Методы проецирования
Если все лучи проецирующие геометрическую фигуру
исходят из одной точки S (находящейся на определенном
расстоянии от плоскости проекций), то такое проецирование
называется центральным.
C
B
C'
П'
S
A'
A
S
П'
B'
B
A
B'
C
A'
C'

7. Центральное проецирование часто называют - ПЕРСПЕКТИВОЙ

Центральное проецирование часто называют ПЕРСПЕКТИВОЙ
• Перспективу применяют при рисовании с натуры, в
архитектуре, строительстве

8. Применение центрального проецирования в жизни

9.

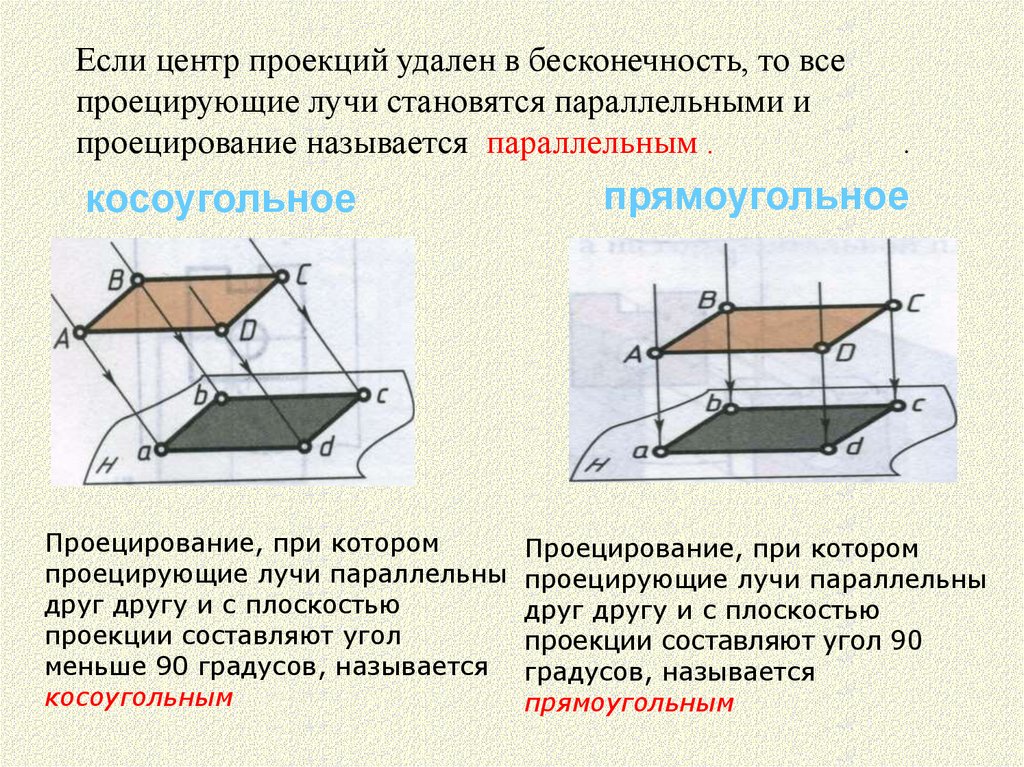
Если центр проекций удален в бесконечность, то все
проецирующие лучи становятся параллельными и
проецирование называется параллельным .
косоугольное
.
прямоугольное
Проецирование, при котором
Проецирование, при котором
проецирующие лучи параллельны проецирующие лучи параллельны
друг другу и с плоскостью
друг другу и с плоскостью
проекции составляют угол
проекции составляют угол 90
меньше 90 градусов, называется градусов, называется
косоугольным
прямоугольным

10. Проецирование точки, отрезка, плоскости

Прописными (заглавными) буквами
обозначаются точки на предмете,
проекции точек на плоскости
обозначаются строчными (малыми)
буквами. Обозначение проекций
невидимых вершин заключают в
скобки

11. Прямоугольное проецирование

V
Вертикальную плоскость проекций (V),
расположенную перед зрителем, называют
фронтальной. Чтобы построить проекцию
предмета, проведем через вершины и точки
отверстий предмета проецирующие лучи,
перпендикулярные плоскости V

12. Фронтальная проекция

V
S6
По полученной проекции мы можем судить о
двух измерениях предмета – высоте и ширине.
Чтобы по такому изображению можно было
судить о форме плоской детали, его
дополняют указанием толщины (S) детали

13.

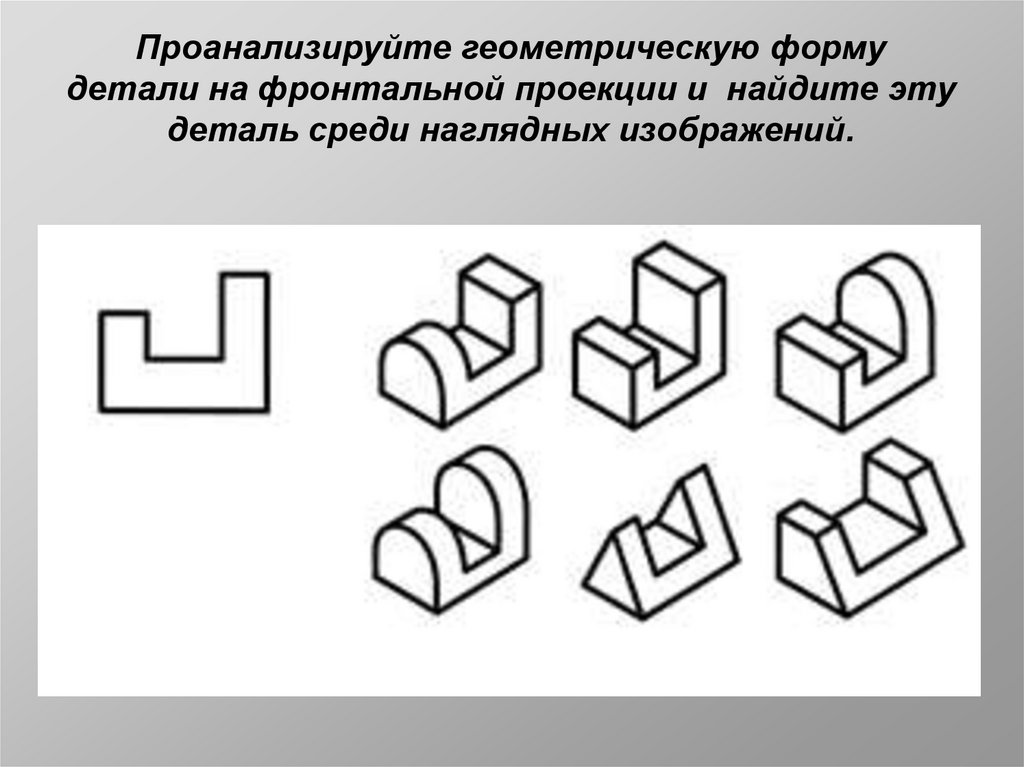
Проанализируйте геометрическую форму
детали на фронтальной проекции и найдите эту
деталь среди наглядных изображений.

14. Прямоугольное проецирование

V
Одна проекция не всегда определяет
геометрическую форму предмета. В таком
случае можно построить две прямоугольные
X проекции предмета на две взаимно
перпендикулярные плоскости: фронтальную
(V) и горизонтальную (Н). Линию пересечения
плоскостей (Х) называют осью проекций
Н

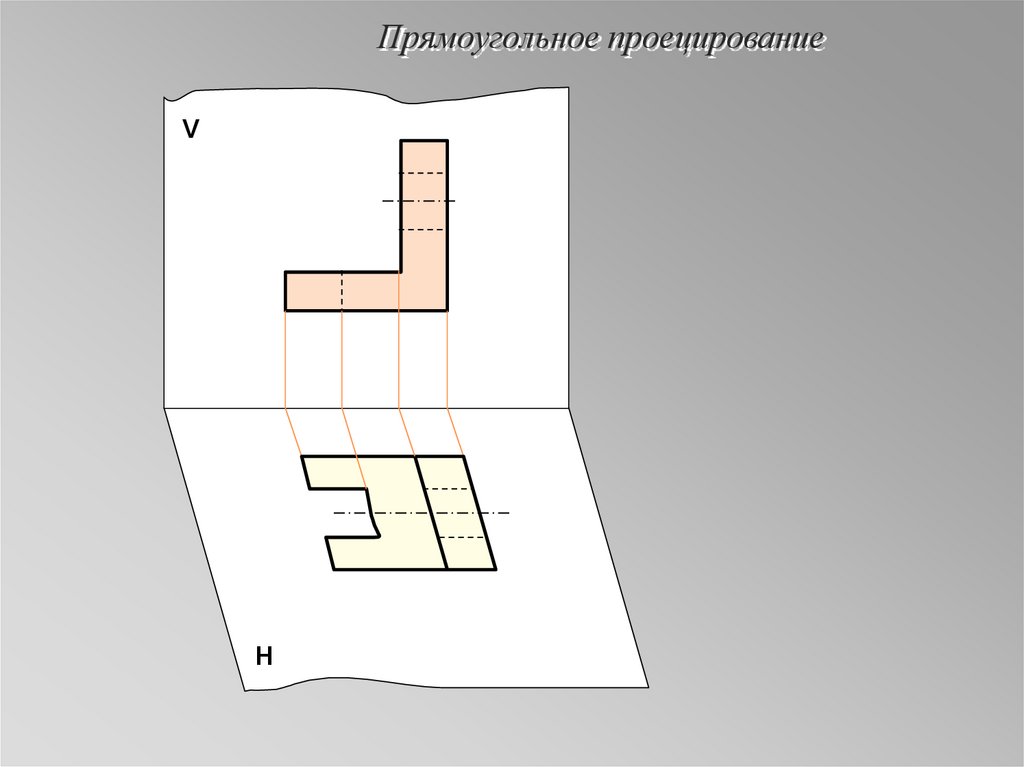
15. Прямоугольное проецирование

V
Построенные проекции оказались
расположенными в пространстве в разных
плоскостях (вертикальной и
горизонтальной). Для получения чертежа
предмета обе плоскости совмещают в одну
Н

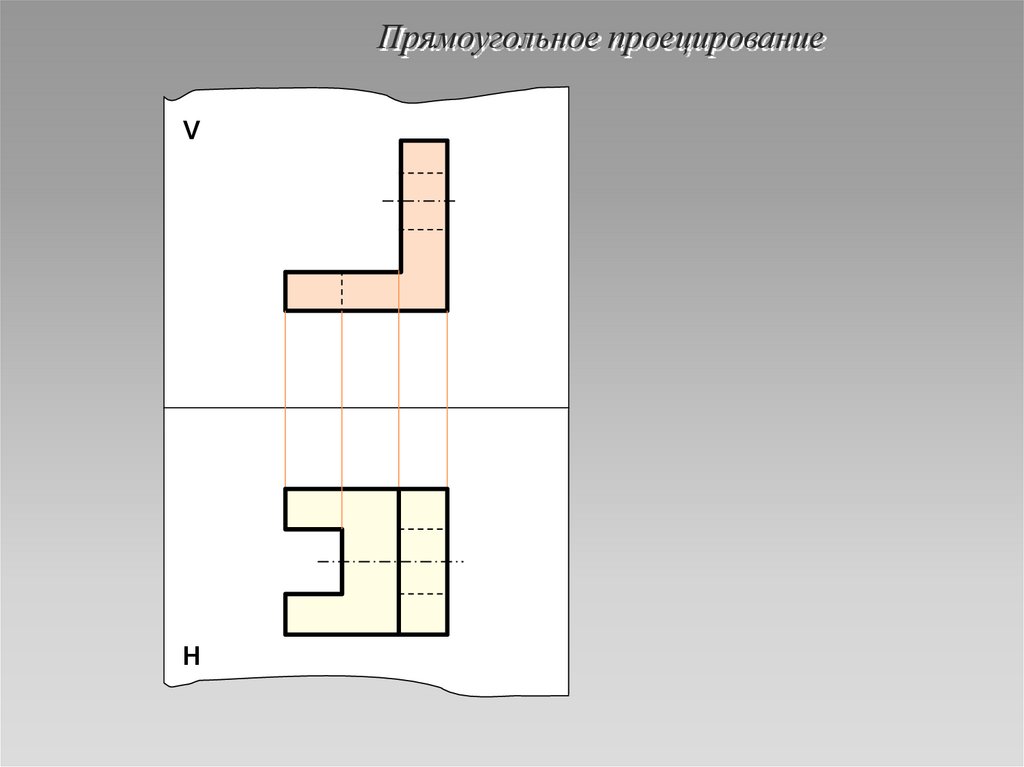
16. Прямоугольное проецирование

V
Н

17. Прямоугольное проецирование

V
Н

18.

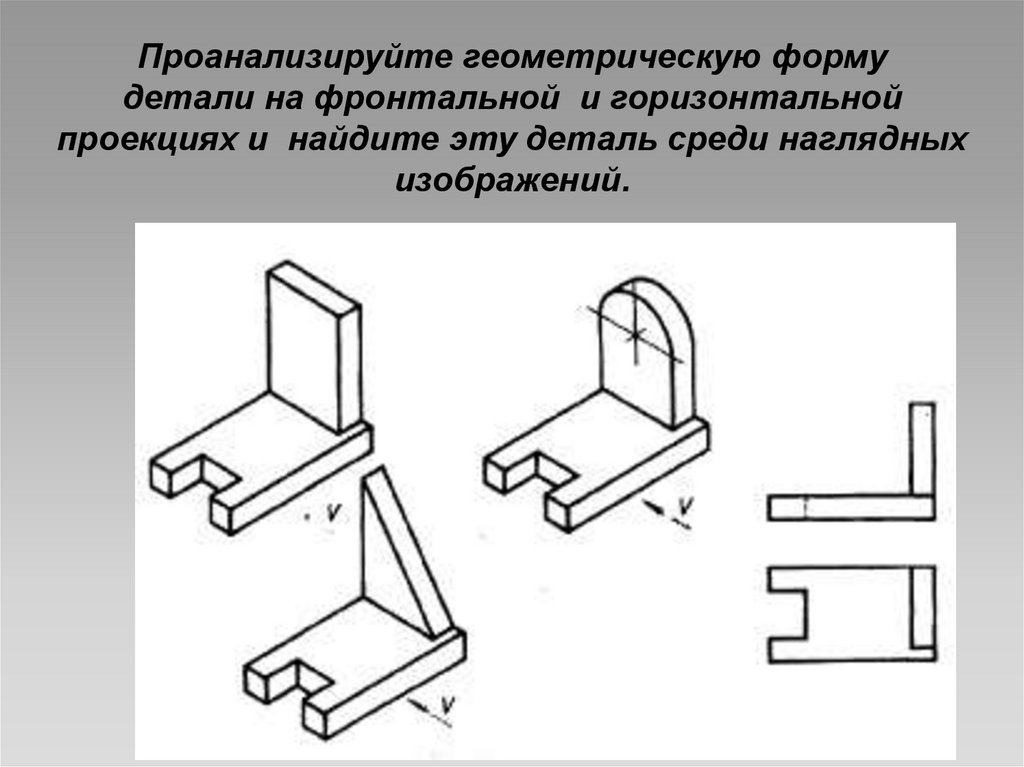
Проанализируйте геометрическую форму
детали на фронтальной и горизонтальной
проекциях и найдите эту деталь среди наглядных
изображений.

19. Прямоугольное проецирование

V
W
Для того, чтобы выявить форму предмета,
не всегда бывает достаточно двух проекций.
В этом случае надо построить еще одну
плоскость. Третью плоскость проекций
называют профильной, а полученную на ней
проекцию – профильной проекцией
предмета. Ее обозначают буквой W
Н

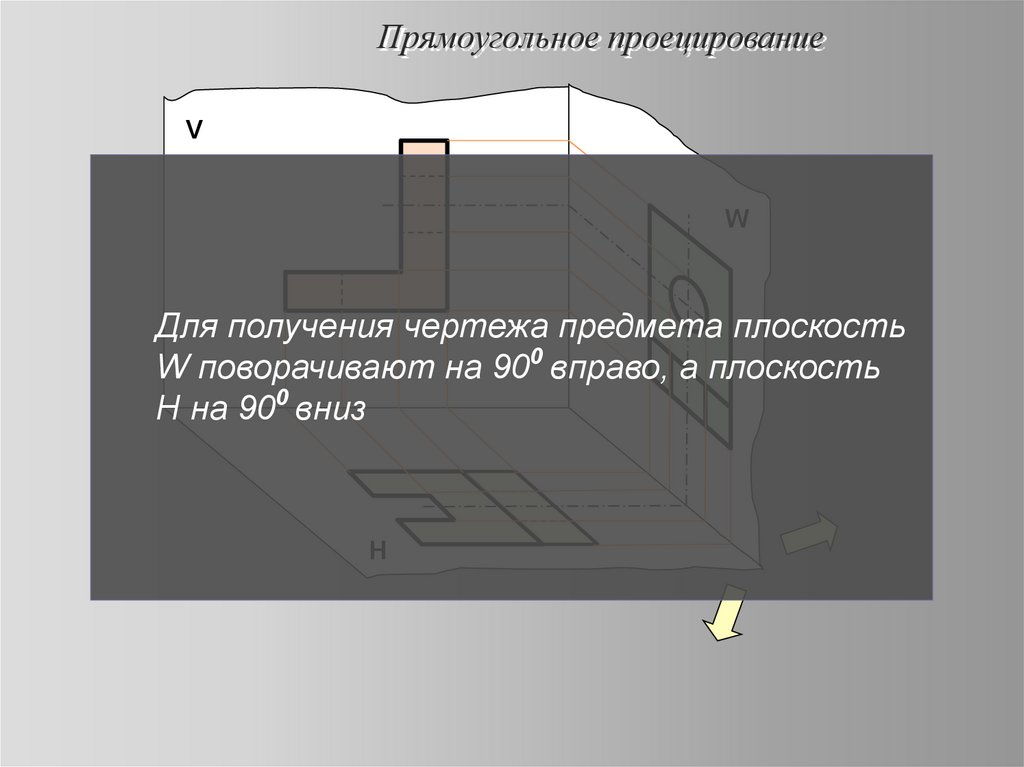
20. Прямоугольное проецирование

V
W
Для получения чертежа предмета плоскость
W поворачивают на 900 вправо, а плоскость
Н на 900 вниз
Н

21. Прямоугольное проецирование

V
W
Н

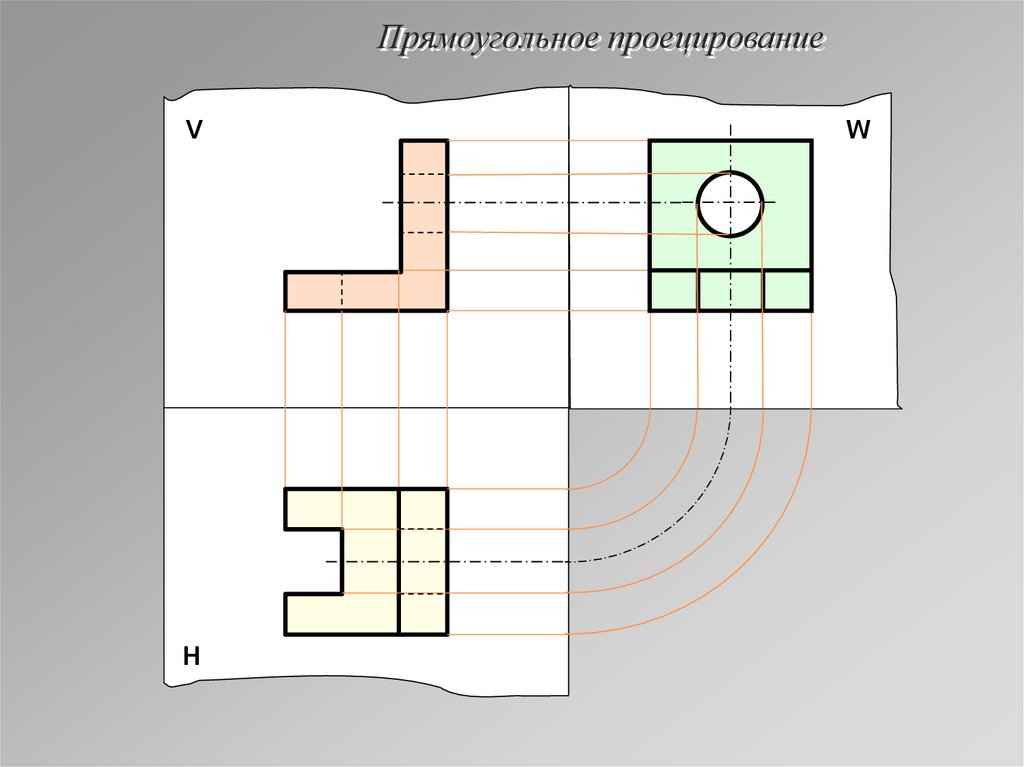
22. Прямоугольное проецирование

V
Н
W

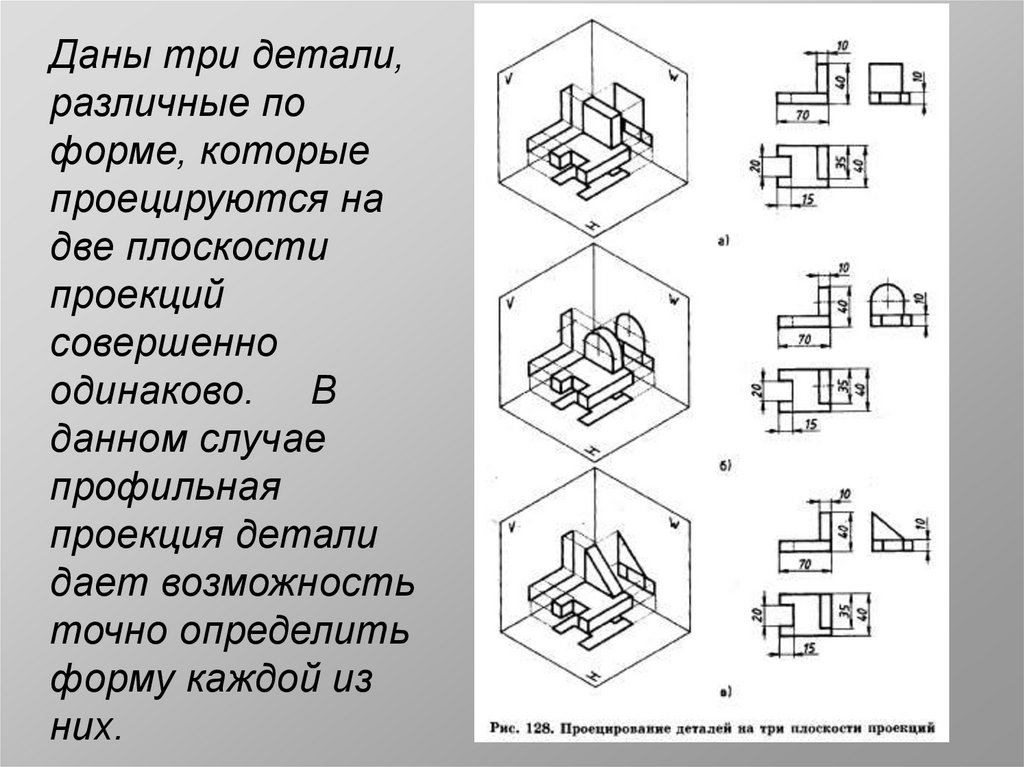
23.

Даны три детали,
различные по
форме, которые
проецируются на
две плоскости
проекций
совершенно
одинаково. В
данном случае
профильная
проекция детали
дает возможность
точно определить
форму каждой из
них.

24. Прямоугольное проецирование

Получившийся таким образом чертеж
содержит три прямоугольные проекции
предмета: фронтальную, горизонтальную
и профильную. Оси проекций и
проецирующие лучи на чертеже не
показывают

25. Прямоугольное проецирование

58
78
18
30
18
Ф 30
На чертеже проекции располагают
в
проекционной связи. Чертеж, состоящий из
60
нескольких прямоугольных проекций,
называют
чертежом в системе прямоугольных
проекций
26
76
Чертил Петров В.
Проверил
Школя № 1274 кл. 9 Б
Стойка
сталь
1:1

26. Прямоугольное проецирование

1. Всегда ли достаточно на чертеже одной
проекции предмета?
2. Как называются плоскости проекций? Как они
обозначаются?
3. Как называются проекции, полученные при
проецировании предмета на три плоскости
проекций? Как располагаются эти плоскости
относительно друг друга?

27.

Точка. Комплексный чертеж точки
Комплексный чертеж точки состоит из двух или трех ортогональных проекций.
Эти проекции получают на взаимно перпендикулярных плоскостях проекций. Одна из
плоскостей проекций H (П1) называется горизонтальной плоскостью проекций, вторая
V (П2)- фронтальной, а третья W (П3) - профильной.
фронтальная
z
Комплексный чертеж точки А
профильная
V
A"
y
А
Проекции точки:
/
A'''
A
x
А//- фронтальная проекция точки А
0
А///х- профильная проекция точки А
o
A'
H
А// w
А/- горизонтальная проекция точки А
W
z
x
z
y
горизонтальная
Линии пересечения плоскостей проекций
называются осями координат x, y, z.
А
y
y

28. Образование комплексного чертежа линии.

Прямая линия в пространстве определяется положением двух ее точек,
например А и B. Значит, достаточно выполнить комплексный чертеж этих
точек, а затем соединить одноименные проекции точек прямыми линиями,
получим соответственно горизонтальную и фронтальную проекции прямой.

29.

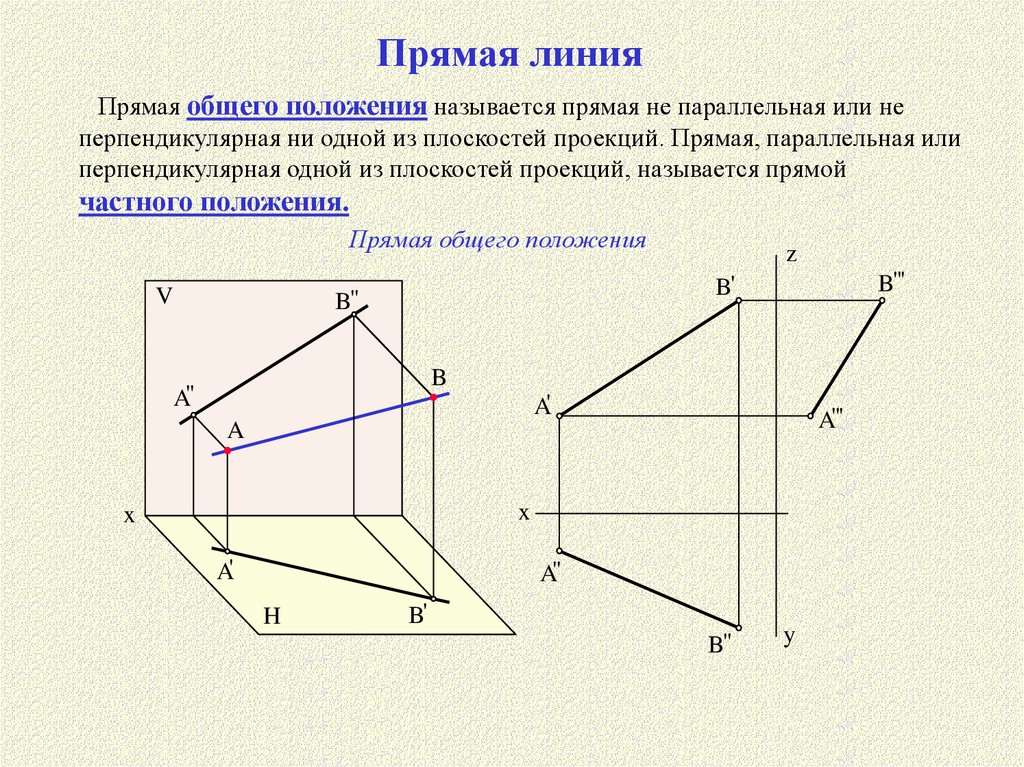
Прямая линия
Прямая общего положения называется прямая не параллельная или не
перпендикулярная ни одной из плоскостей проекций. Прямая, параллельная или
перпендикулярная одной из плоскостей проекций, называется прямой
частного положения.
Прямая общего положения
V
z
B"'
B'
B"
B
A"
A'
A"'
A
x
x
A'
A"
H
B'
B"
y

30.

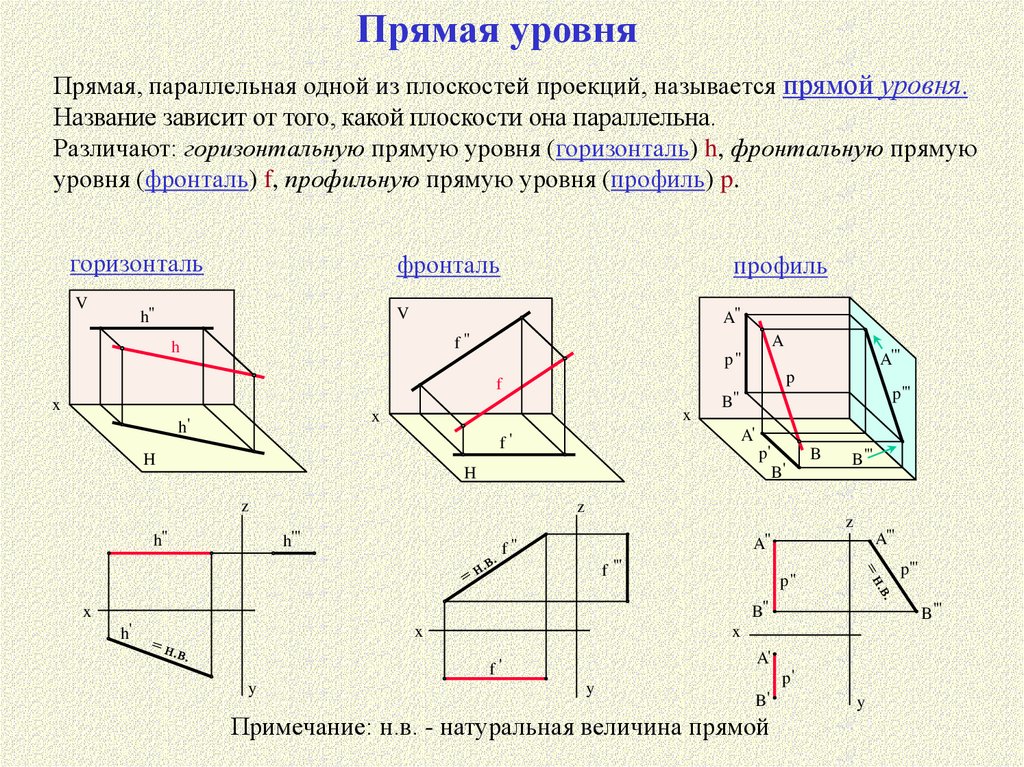
Прямая уровня
Прямая, параллельная одной из плоскостей проекций, называется прямой уровня.
Название зависит от того, какой плоскости она параллельна.
Различают: горизонтальную прямую уровня (горизонталь) h, фронтальную прямую
уровня (фронталь) f, профильную прямую уровня (профиль) p.
горизонталь
V
h"
фронталь
профиль
V
A"
f"
h
A
A'"
p"
p
f
x
x
x
h'
A'
f'
H
p'
B'
H
z
h"
z
h'"
p '"
B"
B
B'"
z
A'"
A"
f"
f '"
p '"
p"
B"
x
h'
x
x
A'
f'
y
B'"
y
p'
B'
Примечание: н.в. - натуральная величина прямой
y

31.

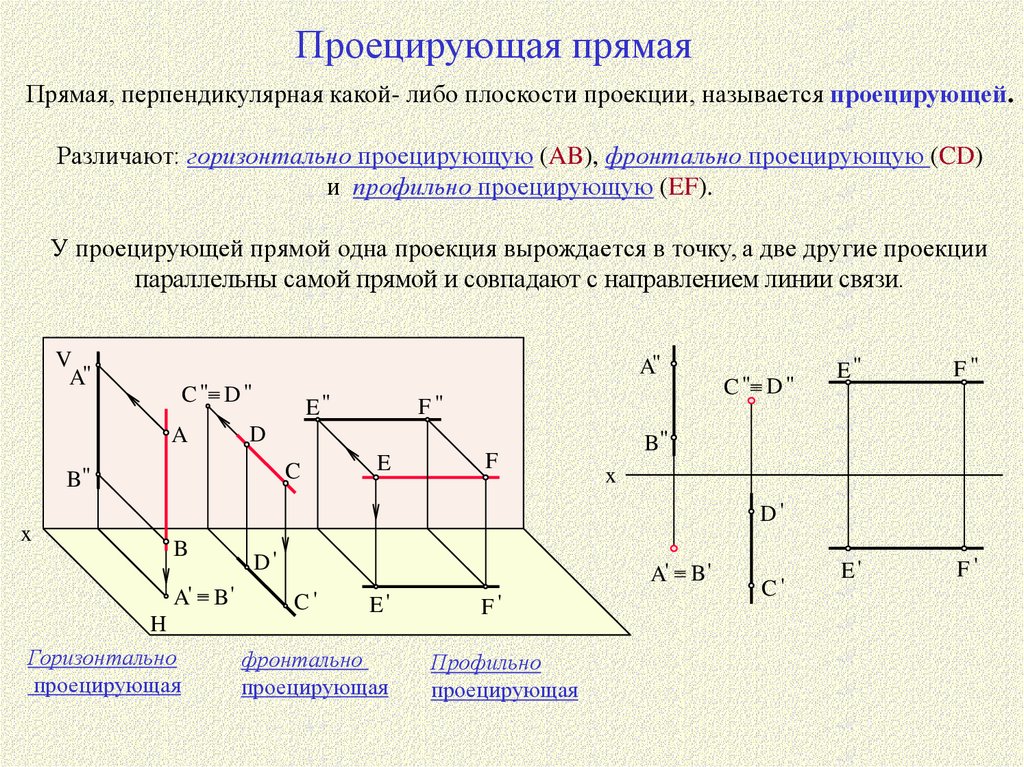
Проецирующая прямая
Прямая, перпендикулярная какой- либо плоскости проекции, называется проецирующей.
Различают: горизонтально проецирующую (AB), фронтально проецирующую (CD)
и профильно проецирующую (EF).
У проецирующей прямой одна проекция вырождается в точку, а две другие проекции
параллельны самой прямой и совпадают с направлением линии связи.
V
A"
A"
_
C "_ D "
A
E"
D
C
B"
x
F"
E
F
_
C "_ D "
E"
F"
E'
F'
B"
x
D'
B
_
A' _ B '
H
Горизонтально
проецирующая
D'
_
A' _ B '
C'
E'
фронтально
проецирующая
F'
Профильно
проецирующая
C'

32.

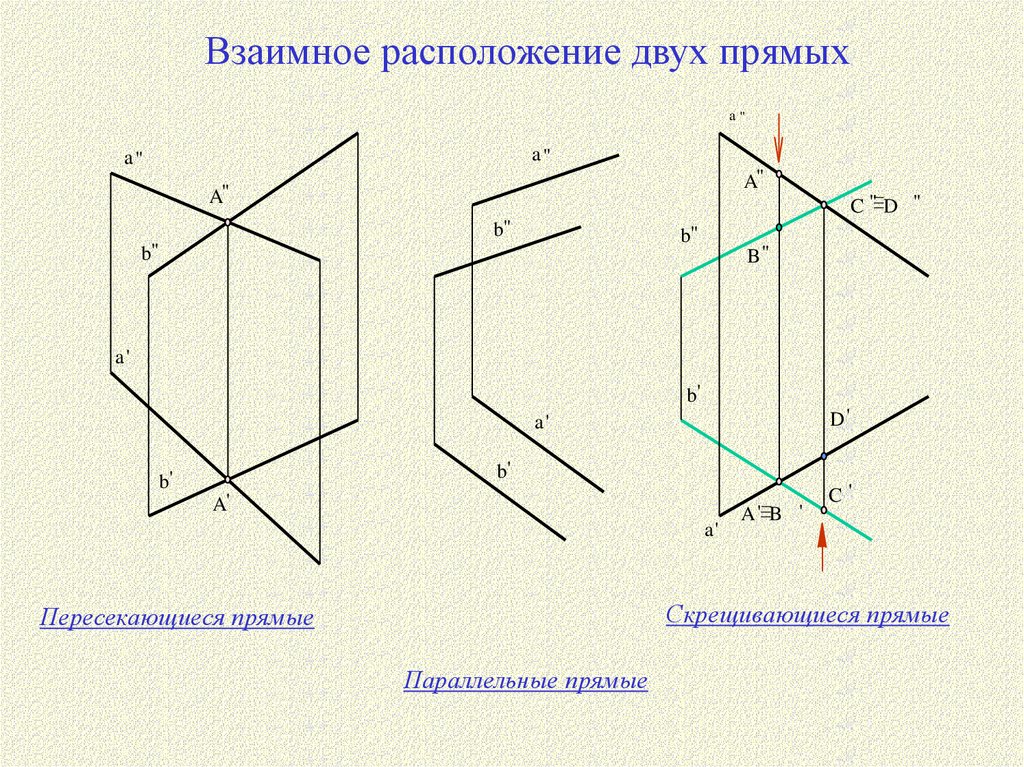
Взаимное расположение двух прямых
a"
a"
a"
A"
A"
b"
b"
b"
__
C "_D "
B"
a'
b'
D'
a'
b'
b'
A'
a'
__
A '_B '
C'
Скрещивающиеся прямые
Пересекающиеся прямые
Параллельные прямые

33.

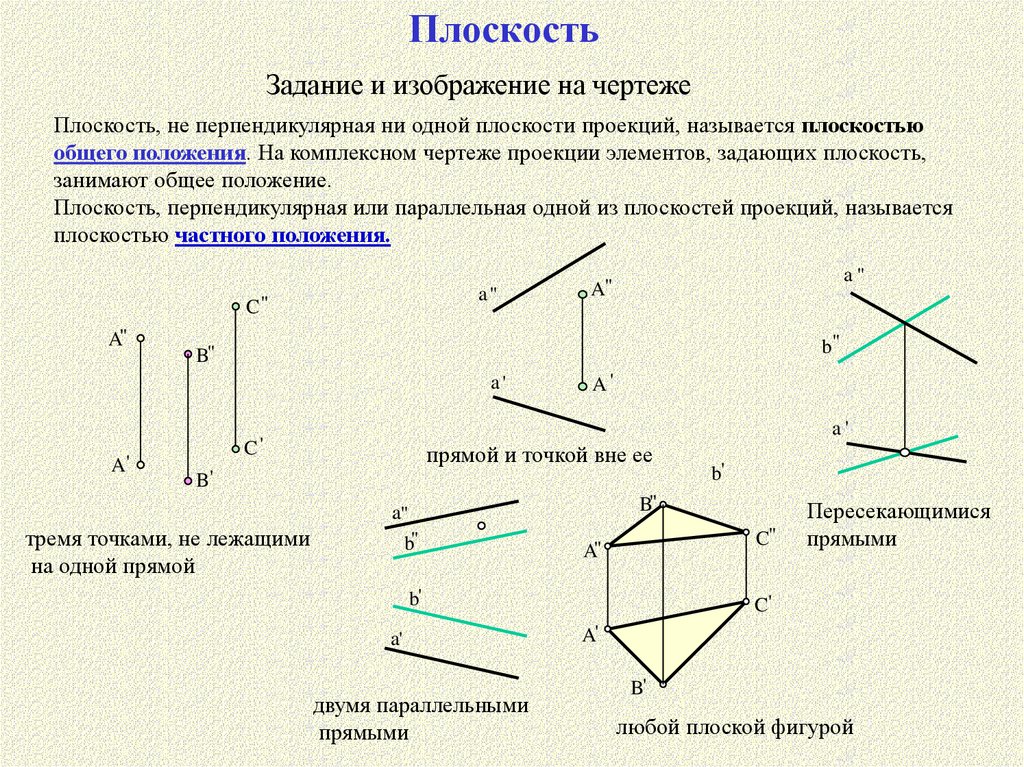
Плоскость
Задание и изображение на чертеже
Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью
общего положения. На комплексном чертеже проекции элементов, задающих плоскость,
занимают общее положение.
Плоскость, перпендикулярная или параллельная одной из плоскостей проекций, называется
плоскостью частного положения.
a"
C"
A"
b"
B"
a'
A'
a"
A"
A'
a'
C'
прямой и точкой вне ее
B'
B"
a"
тремя точками, не лежащими
на одной прямой
b'
b"
C"
A"
b'
a'
двумя параллельными
прямыми
Пересекающимися
прямыми
C'
A'
B'
любой плоской фигурой