Similar presentations:
Математико-статистическое методы в педагогических исследованиях
1. МАТЕМАТИКО-СТАТИСТИЧЕСКОЕ МЕТОДЫ В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
2. Классификация шкал измерений
3.
1. Номинальная шкала (шкала наименований)Примеры:
1) Учащиеся класса делятся на две категории и обозначаются:
девочки - 01, мальчики - 02.
2) Группы нарушителей дисциплины и их обозначение
(кодирование): на уроке - 1, на улице – 2, дома - 3.
3) В процессе проверки соответствия подготовки выпускников
школ требованиям ГОС появляется группа аттестованных и не
аттестованных учеников.
4) Подсчет «отличников», «хорошистов», «двоечников» и
сравнение этих групп по количеству учащихся
4.
2. Шкала порядка(порядковая, ранговая, ординальная)
предназначена для измерения (обозначения) степени
различия какого-либо признака или свойства у разных
объектов.
Пример: пятибалльная система оценки ЗУН учащихся.
Недопустимо вычисление среднего балла!
Имеется несколько разновидностей порядкового
шкалирования (измерения):
·
ранжирование (в ряд),
·
группировка (ранжирование по группам),
·
парное сравнение,
·
метод рейтинга,
·
метод полярных профилей.
5.
3. Интервальная шкала (интервальноенамерение)
- присвоение чисел объектам, когда определено расстояние между
объектами и предусмотрена общая для всех объектов постоянная
единица измерения.
Иначе говоря, произвольно выбирается нулевая точка шкалы. Далее
в интервальной шкале вводится единица и масштаб измерения.
Примеры: температурные шкалы; шкалы стандартизированного
тестирования интеллекта.
6.
3. Интервальная шкала (интервальноенамерение)
Интервальная шкала – количественная.
Пример: тестовая технология контроля качества подготовки учеников
Разрешены все арифметические действия над числами, кроме
операции деления.
ТО ЕСТЬ , в интервальной шкале нельзя определить во сколько раз
один объект больше или меньше другого.
Например, если ученик ответил правильно на 10 заданий, то это не
означает, что он знает вдвое больше ученика, ответившего на 5
заданий теста.
7.
4. Шкала отношенийОтличие от интервальной: нулевая точка не произвольна, а указывает на
полное отсутствие измеряемого свойства.
Сюда относятся и все количественные данные, получаемые пересчетом
объектов какого-либо множества (число учащихся, уроков и т. п.).
Измеряются почти все физические величины, но неприменимы в
социальным измерениям
8.
Среднее арифметическоеряда чисел - частное от деления суммы
этих чисел на число слагаемых
Задача:
Сколько минут тратят на домашнее задание
по алгебре ученики 9 класса в среднем,
если время каждого из них 23, 30, 25, 20, 34,
25, 30, 34, 35,14 минут?
23+30+25+20+34+25+30+34+35+14 = 27
10
9.
Модой ряда чисел- называется число, наиболее часто
встречающееся в данном ряду. Мода
отражает наиболее типичный признак.
Какое число являет ся модой данного ряда?
20
25
34
32
25
23
34
25
26
32
18
25
37
10. МОДА
вариационныйдискретный
ряд
вариационный
интервальный
ряд
определяется
по наибольшей
частоте
признака
определяется по
специальной
методике
11. МОДА в интервальном ряду
• Определяется модальный интервал –по наибольшей частоте
• Рассчитывается значение моды по
формуле
12. Расчет моды в интервальном ряду
M o xo ho *f M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
xo
-начало модального интервала
ho
-длина модального интервала
f Mo
f Mo 1
-частота модального интервала
f Mo 1
-частота интервала, предшествующего модальному
-частота интервала, следующего за модальным
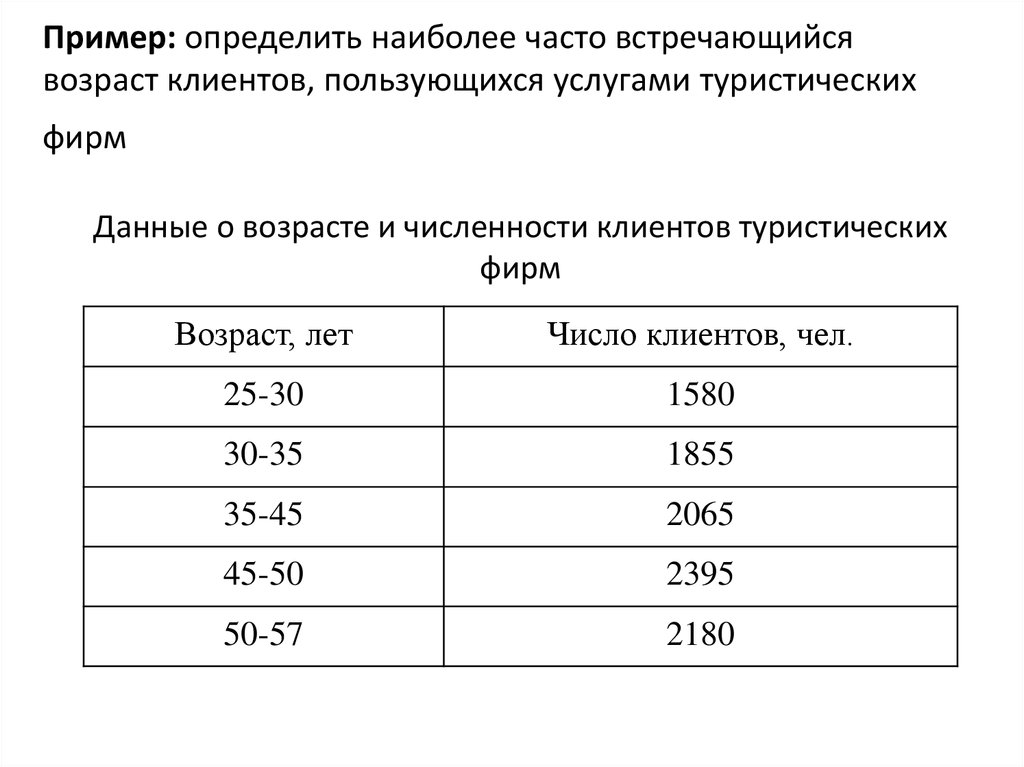
13. Пример: определить наиболее часто встречающийся возраст клиентов, пользующихся услугами туристических фирм
Данные о возрасте и численности клиентов туристическихфирм
Возраст, лет
Число клиентов, чел.
25-30
1580
30-35
1855
35-45
2065
45-50
2395
50-57
2180
14. Мо = 45+5* 2395-2065 (2395-2065)+(2395-2180)
= 48,03Чаще всего в туристические фирмы
обращаются клиенты, возраст которых
составляет около 48 лет
15.
Размах ряда чисел- разность между наибольшим и наименьшим
из этих чисел.
Пример:
дан упорядоченный ряд чисел
34, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
39 – 34 = 4 - размах ряда
16. Медиана (Ме)
значение признака, находящегося всередине ряда распределения.
Медиана делит вариационный ряд на две
равные части: одна часть имеет
значения варьирующего признака
меньшие, чем медиана, другая большие.
17. МЕДИАНА
вариационныйдискретный
ряд
вариационный
интервальный
ряд
серединное
значение
признака
определяется по
специальной
методике
18.
Медианой упорядоченного ряда чиселс нечётным числом членов называется среднее в ряду
число;
с чётным числом членов среднее арифметическое
чисел, записанных посередине
1)
64, 72, 72, 75, 78, 82, 85, 91, 93
2) 64, 72, 72, 75, 78, 82, 85, 88, 91, 93
78+82 = 80
2
19. МЕДИАНА в интервальном ряду
• Определяется медианный интервал –по накопленным (кумулятивным)
частотам
• Рассчитывается значение медианы по
формуле
20. Расчет медианы в интервальном ряду
Mexe
he
f i
S M e 1
xe he * 2
fMe
- начало медианного интервала
- длина модального интервала
S Me 1 - кумулятивная частота интервала, предшествующего
f Me
медианному
- частота медианного интервала (не накопленная)
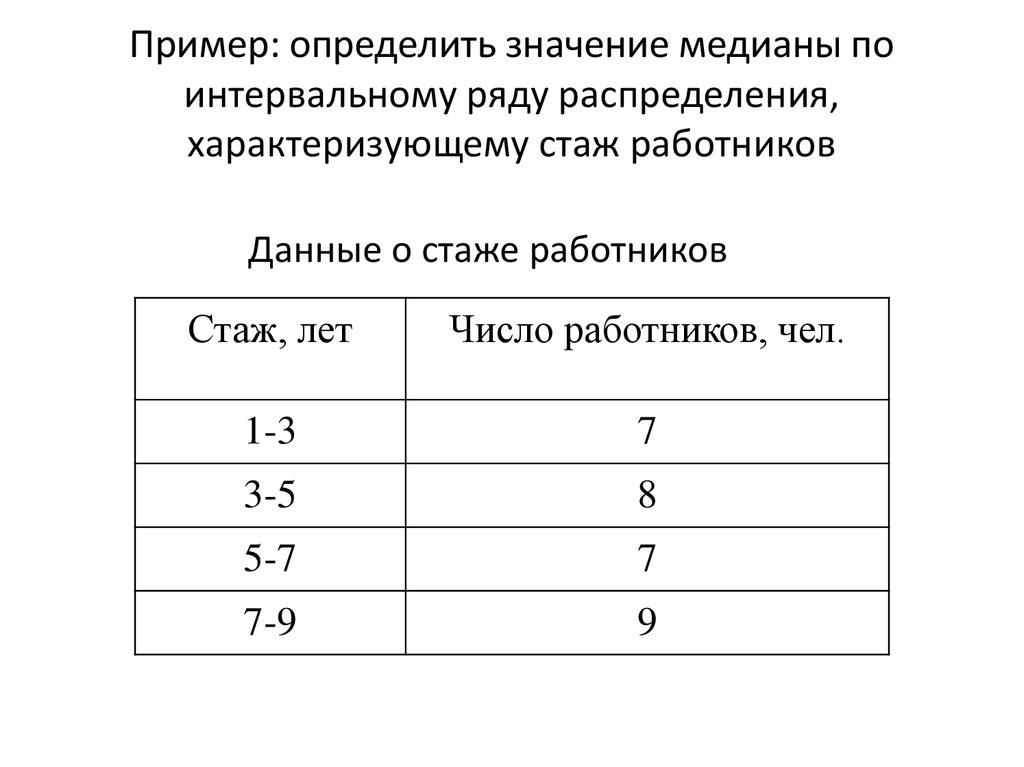
21. Пример: определить значение медианы по интервальному ряду распределения, характеризующему стаж работников
Данные о стаже работниковСтаж, лет
Число работников, чел.
1-3
7
3-5
8
5-7
7
7-9
9
22.
Данные о стаже работников1-3
Число работников,
чел.
7
Накопленные
частоты
7
3-5
8
15
5-7
7
22
7-9
9
31
Стаж, лет
1. Половина накопленных частот 15,5 (31/2=15,5)
2. Медианным является интервал от 5 до 7 лет,
(так как 15,5 больше чем 7 и 15, но меньше 22)
23.
Ме=5+2* 15,5-15 = 5,1 года7
по данному ряду распределения
половина работников
имеет стаж менее 5,1 года,
половина более 5,1 года
24. СПОСОБЫ ВЫЧИСЛЕНИЯ ДОСТОВЕРНОСТИ РАЗЛИЧИЙ МЕЖДУ ДВУМЯ ЗАВИСИМЫМИ РЕЗУЛЬТАТАМИ
25.
В случае, когда мы имеем дело с результатами,полученными
- в начале и в конце
- на разных этапах проведения эксперимента
в одной и той же группе эти результаты считаются
зависимыми (связанными, сопряженными)
26. Интервальная шкала или шкала отношений
Определение достоверности различий междудвумя зависимыми результатами на основе
t – критерия Стьюдента
27.
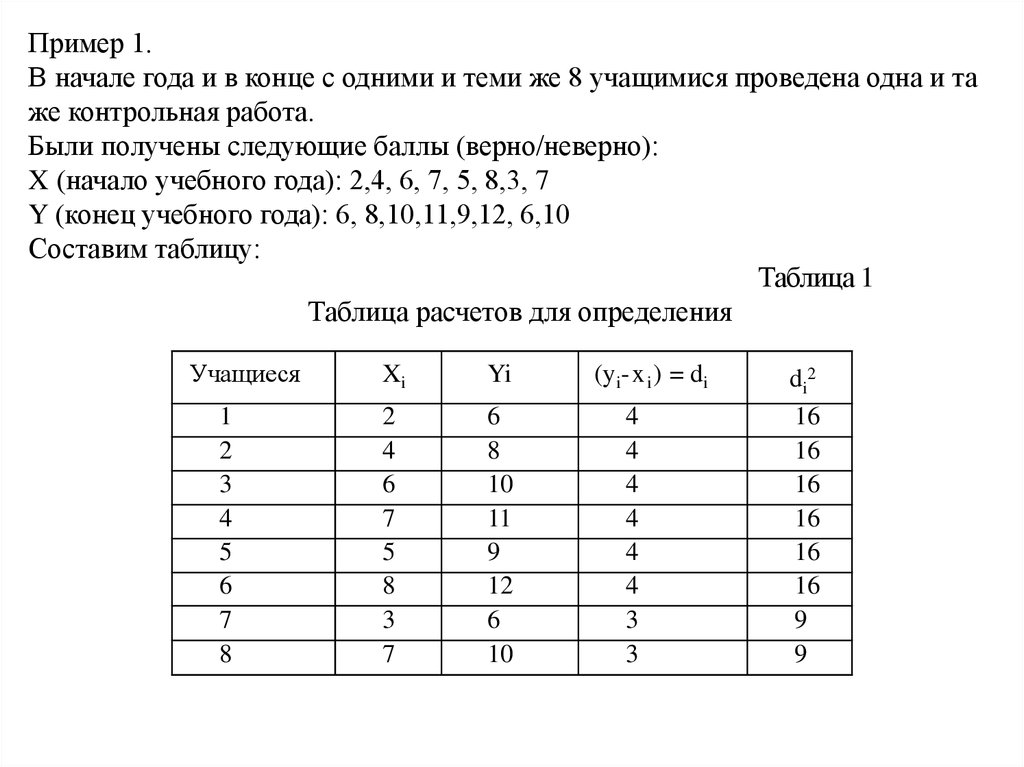
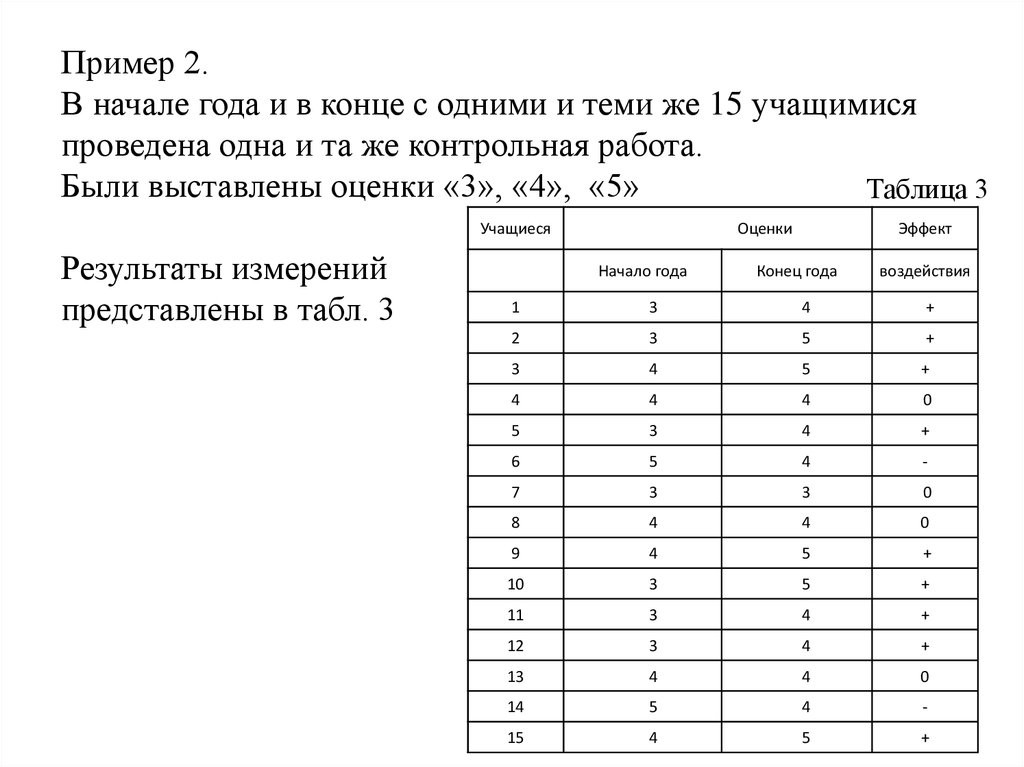
Пример 1.В начале года и в конце с одними и теми же 8 учащимися проведена одна и та
же контрольная работа.
Были получены следующие баллы (верно/неверно):
X (начало учебного года): 2,4, 6, 7, 5, 8,3, 7
Y (конец учебного года): 6, 8,10,11,9,12, 6,10
Составим таблицу:
Таблица 1
Таблица расчетов для определения
Учащиеся
1
2
3
4
5
6
7
8
Xi
Yi
2
4
6
7
5
8
3
7
6
8
10
11
9
12
6
10
(yi-x i ) = di
4
4
4
4
4
4
3
3
di2
16
16
16
16
16
16
9
9
28.
1. Подсчитать среднюю разность, сумму разностей, суммуквадратов разностей:


































 mathematics
mathematics








