Math relation and function

1.

MATH
RELATION AND FUNCTION
by TULEGENOVA KAMSHAT

2.

3.

4.

Outline
Introduction to relation
Introduction to function/Types of functions
Domain and range
x and y intercept

5.

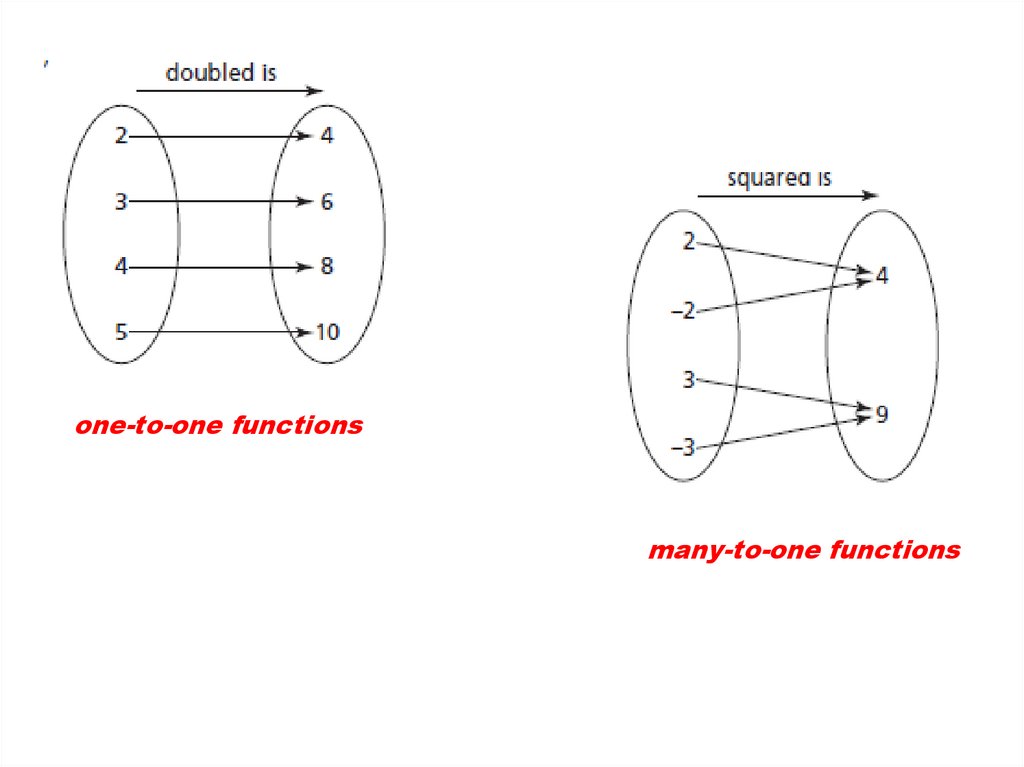
A function is a special type of
relation where each element in
the one set is
associated with exactly one
element in the other set.

6.

one-to-one functions
many-to-one functions

7.

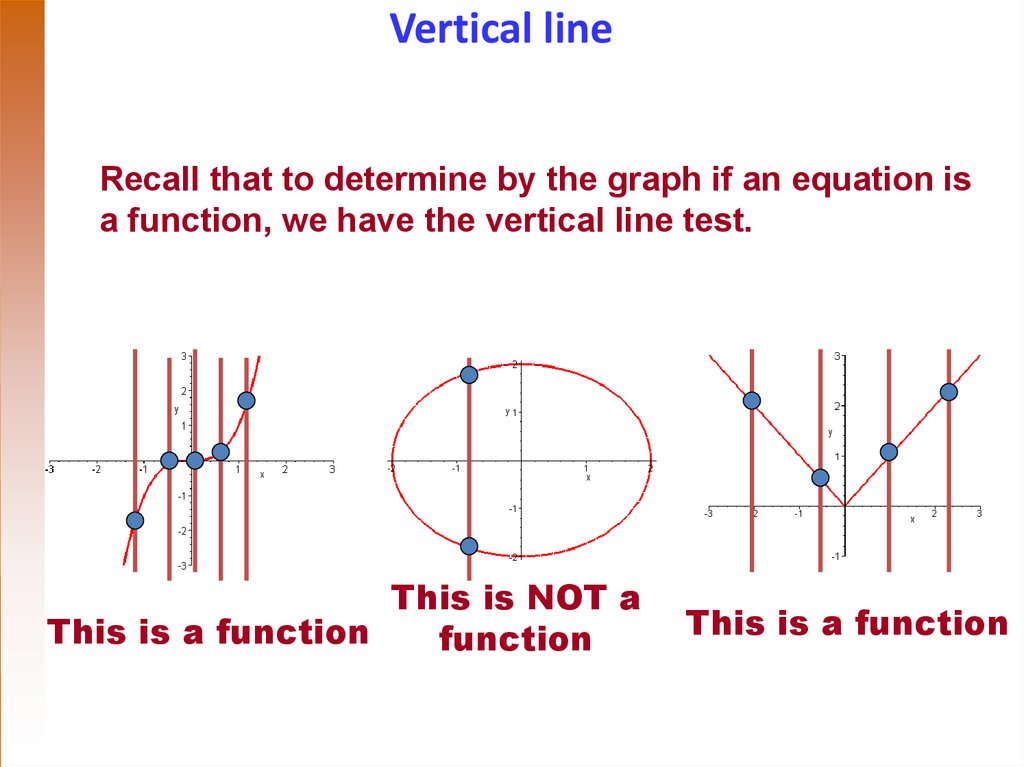
Vertical line
Recall that to determine by the graph if an equation is
a function, we have the vertical line test.
This is NOT a
This is a function
function
This is a function

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

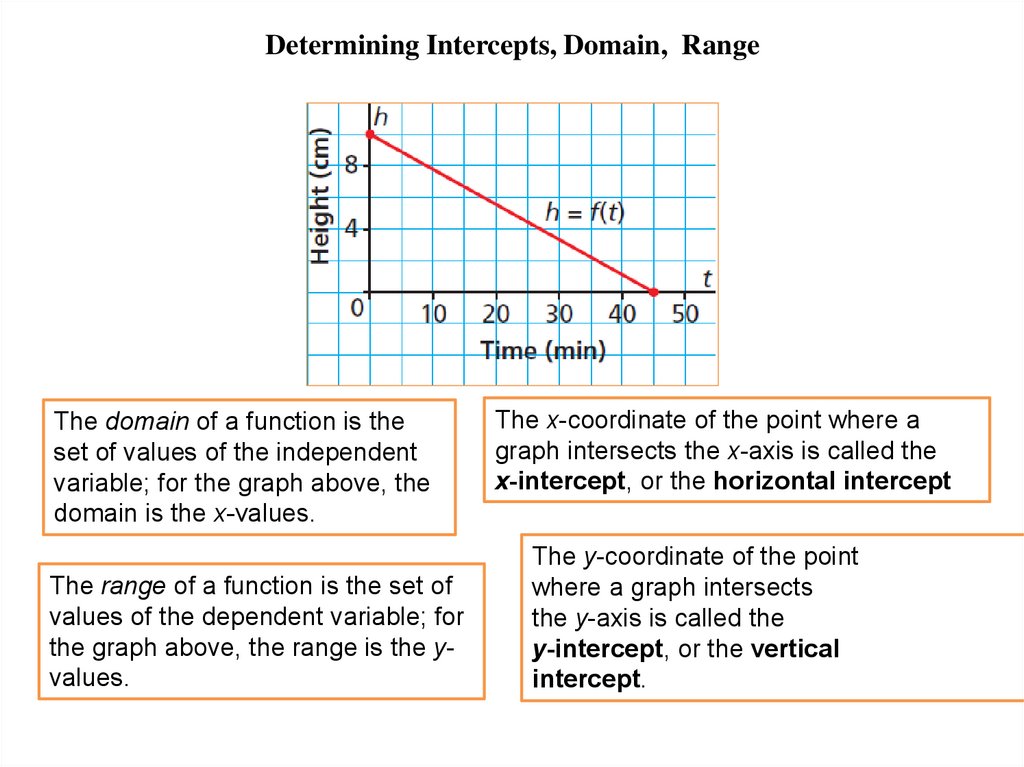
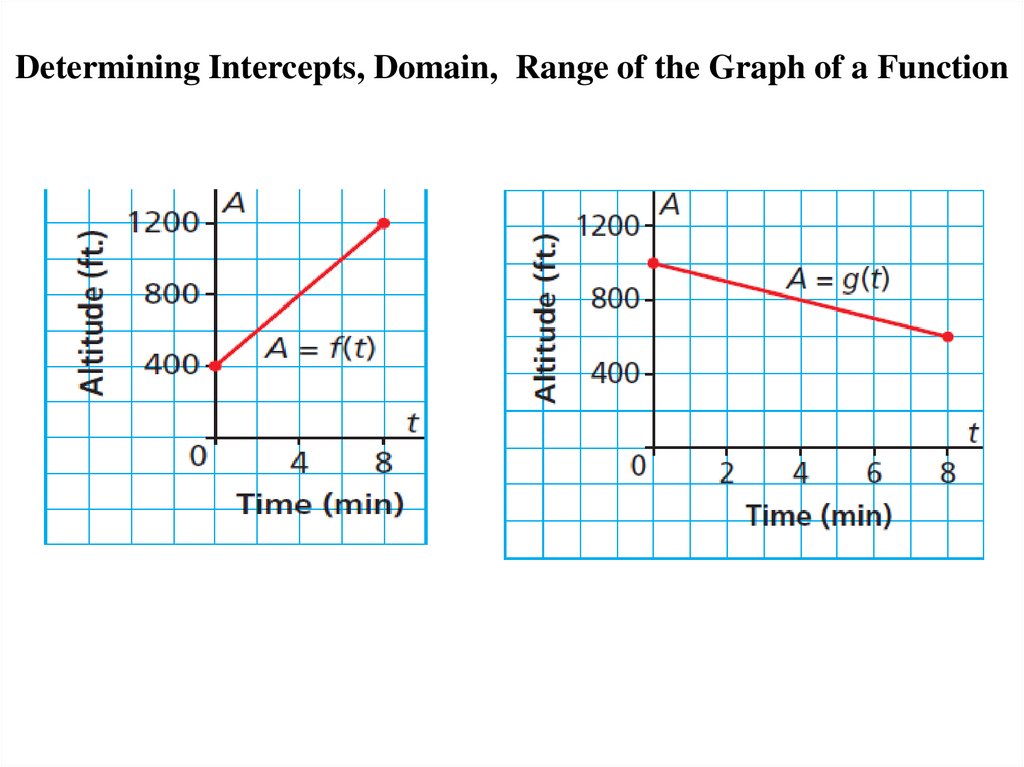
Determining Intercepts, Domain, Range
The domain of a function is the
set of values of the independent
variable; for the graph above, the
domain is the x-values.
The range of a function is the set of
values of the dependent variable; for
the graph above, the range is the yvalues.
The x-coordinate of the point where a
graph intersects the x-axis is called the
x-intercept, or the horizontal intercept
The y-coordinate of the point
where a graph intersects
the y-axis is called the
y-intercept, or the vertical
intercept.

18.

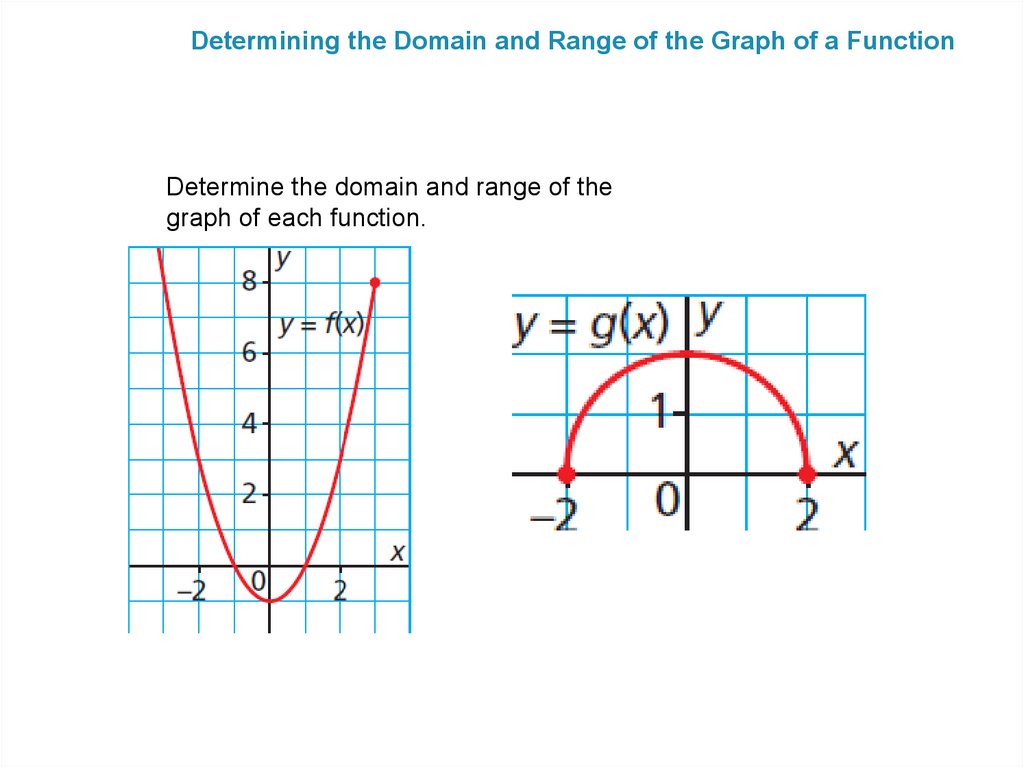
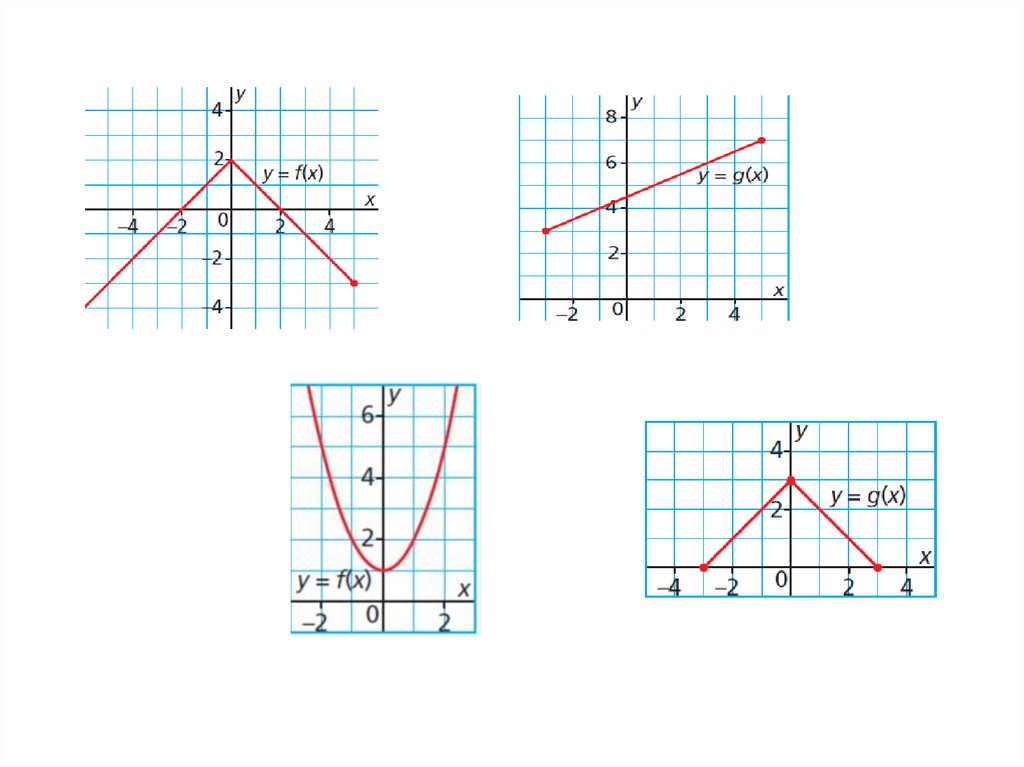
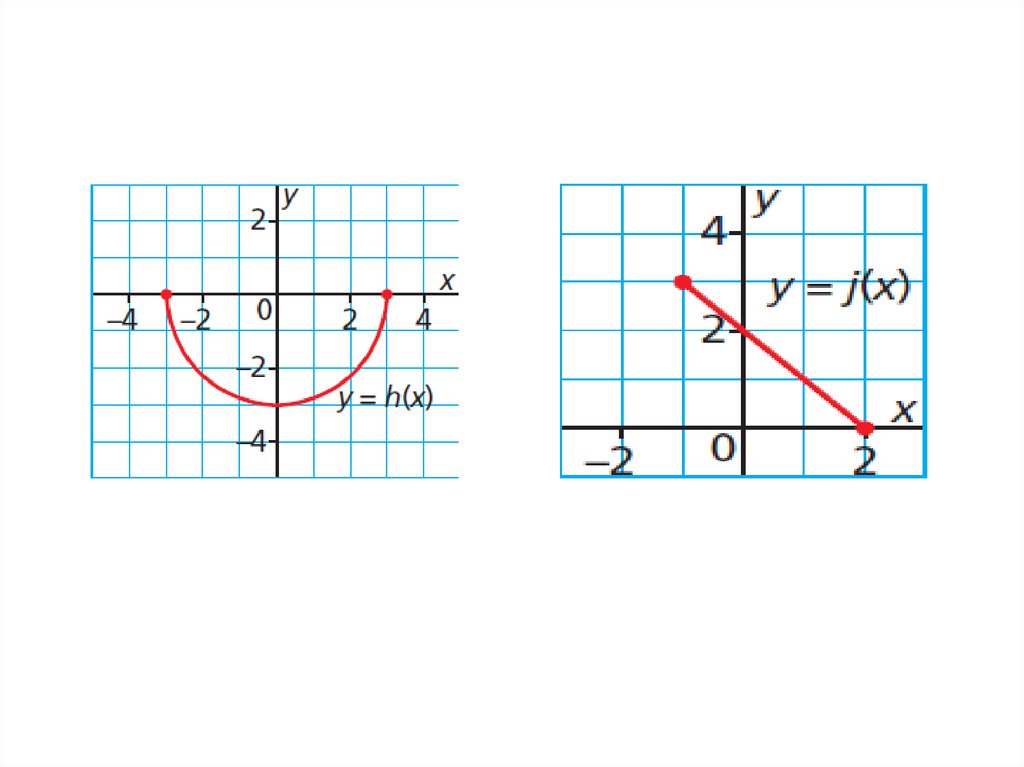
Determining the Domain and Range of the Graph of a Function
Determine the domain and range of the
graph of each function.

19.

20.

21.

Determining Intercepts, Domain, Range of the Graph of a Function

22.

23.

Even functions
If a function is such that f(–x) = f(x) for all values
of x, it is called an even function.
For example, show that f(x) = 3x4 – x2 + 2
is an even function.
f(–x) = 3(–x)4 – (–x)2 + 2
= 3x4 – x2 + 2
= f(x)
f(–x) = f(x), so the function is even.
Can you write down another even function?

24.

Graphs of even functions
Here are the graphs of some even functions:
y
y
y
x
x
x
What do you notice about these graphs?
The graphs of all even functions are
symmetric about the y-axis.

25.

Odd functions
If a function is such that f(–x) = –f(x) for all values
of x, it is called an odd function.
For example, show that f(x) = x3 + 4x is
an odd function.
f(–x) = (–x)3 + 4(–x)
= –x3 – 4x
= –(x3 + 4x)
= –f(x)
f(–x) = –f(x), so the function is odd.
Can you write down another odd function?

26.

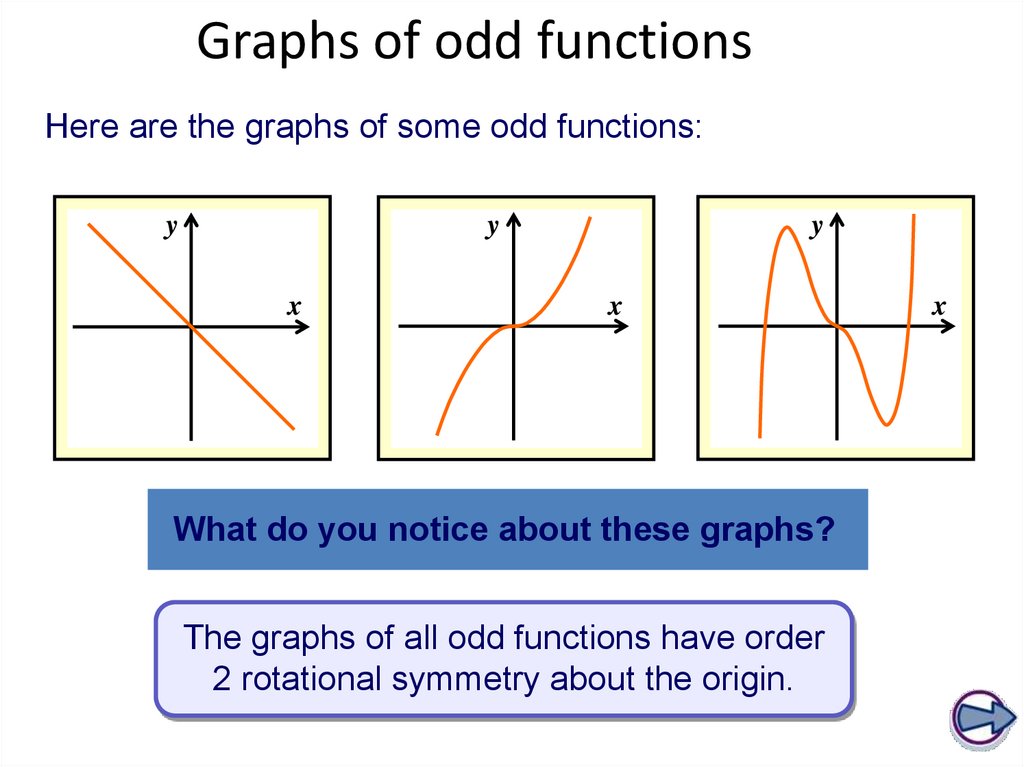
Graphs of odd functions
Here are the graphs of some odd functions:
y
y
x
y
x
What do you notice about these graphs?
The graphs of all odd functions have order
2 rotational symmetry about the origin.
x

27.

28.

29.

30.

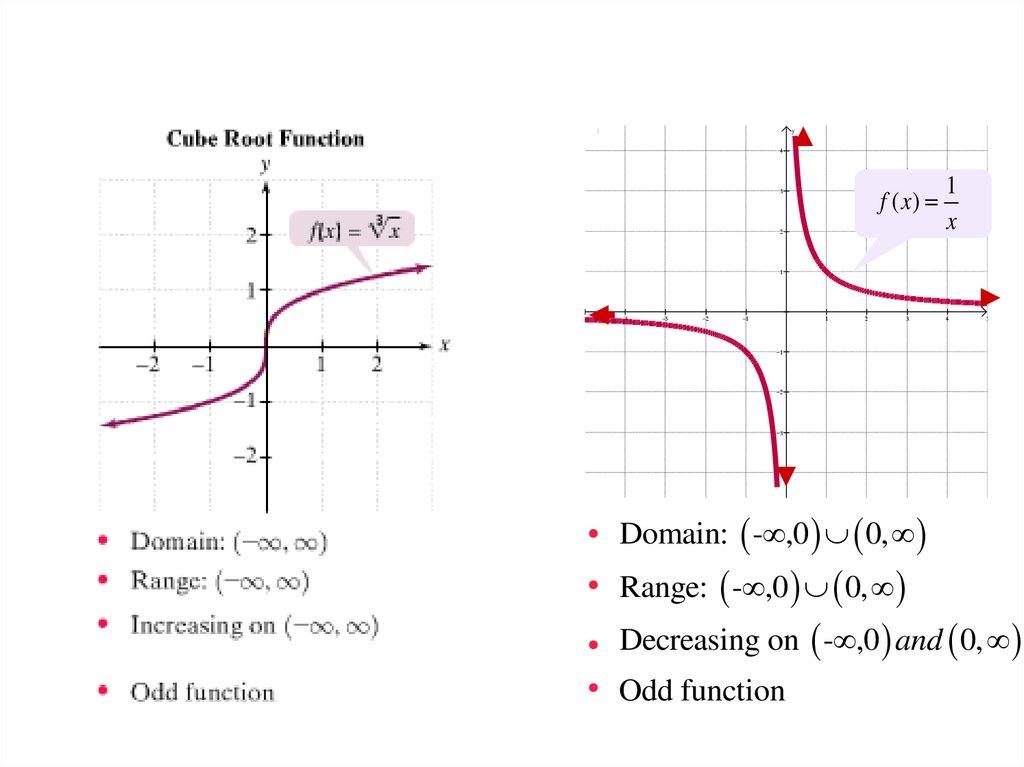
Reciprocal Function
y
f ( x)
1
x
x
Domain: - ,0 0,
Range: - ,0 0,
Decreasing on - ,0 and 0,
Odd function

31.

32.

Literature
1.
https://byjus.com/maths/rational-function/
2. https://www.analyzemath.com/rational/rational1.html
3. https://oregonstate.edu/instruct/mth251/cq/FieldGuide/rational/less
on.html

33.

Do you have any questions?