Presentation

1.

Differential
Equations
:3

2.

Дифференциальное
уравнение
• Уравнение, содержащее y', x,
y.
• Примеры:
y' + 2xy = 6
xy' + 3y = 5x
8x^2 – 30yy' = 35

3.

Решение
• Решением дифференциального
уравнения является функция
y(x) (в отличае от знакомых
уравнений, в которых решением
является число).
• А теперь о том, как найти эту
функцию...

4.

Нынешние
возможности
• Построить график производных в
каждой точке
• Воспользоваться фактором
интегрирования
• Подстановка в гомогенных
уравнениях

5.

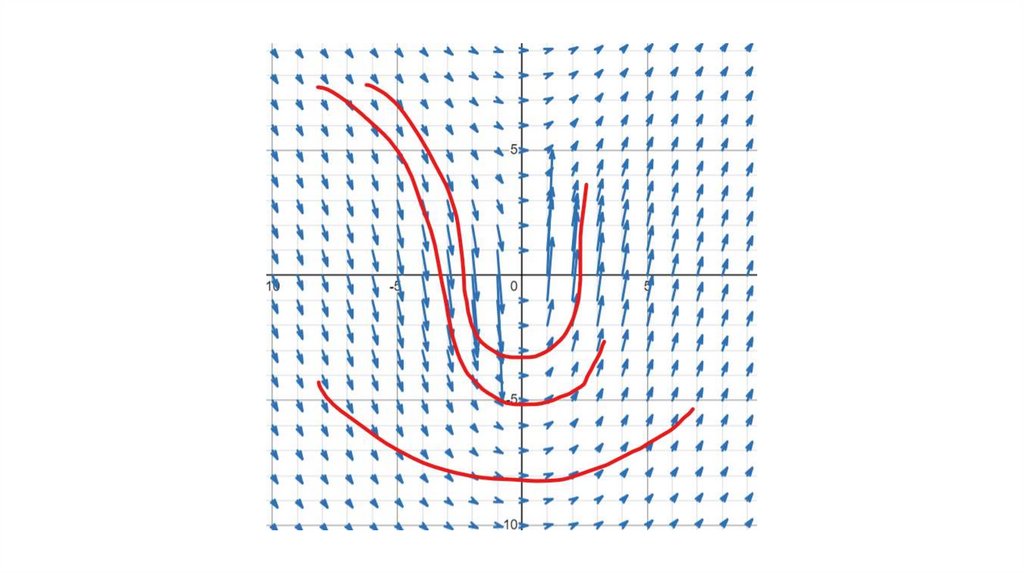
График
производных
в каждой
точке
• Как мы можем знать производная графика в точке
- его наклон.
• Поэтому выразив y' в
дифференциальном
уравнении мы сможем
получить график всех
решений.

6.

И в итоге у нас
получится...
• Решение для уравнения

7.

8.

Фактор
Интегрирования
• Дифференциальное
уравнение первого порядка
имеет вид
y' + p(t)y = q(t)
• Мы можем получить фактор
интегрирования подставив

9.

Фактор
Интегрирования
• Перемножив обе стороны
уравнения на фактор
интегрирования мы получим
удобную запись:
• В которой можно проследить
производную в левой части
уравнения

10.

Фактор
Интегрирования
• Затем, интегрируя обе стороны
уравнения мы получим ответ!

11.

Гомогенные
уравнения
• Уравнение является гомогенным, если
каждый член его может быть
представлен в виде y/x. Или более
просто: каждый член полинома имеет
одинаковую степень гомогенности.
• Например xy^2 имеет 3 степень
гомогенности, так как степень x – 1, а
степень y – 2, что в сумме даёт 3.

12.

Гомогенные
уравнения
• Таким образом мы можем
произвести подстановку u =
y/x, что также значит y = ux, а
y' = u + xu'.
• И результатом будет
дифференциальное уравнение
первого порядка, которое мы
решаем уже известными
способами.

13.

Уравнения
Бернулли
• Иногда дифференциальное уравнение
может иметь вид
y' + p(x)y = y^n * q(x).
• В таких случаях мы говорим об
уравнениях Бернулли.

14.

Уравнения
Бернулли
• Решение будет следующим:
o Создаём переменную u, равную
y^(1 - n).
o Тогда в обратную сторону y = u
^(1 / (1 - n)).
• Теперь поделим всё уравнение на
y^n. В результате мы получим: y^n * y' + y^ (1 - n) * p(x) = q(x).
• Но мы можем выразить y^(-n) * y'
через u, и это будет -1/n * u'.
• Итого уравнение имеет вид: -1/n *
u' + u * p(x) = q(x), а это уже
уравнение первого порядка,
которое мы умеем решать.

15.

Вот и всё,
finita la
commedia