Similar presentations:
Элементы комбинаторики, теории множеств и математической логики
1.
Элементы комбинаторики,теории множеств и
математической логики
Жук И.А.
1
2.
Принципы обработки информациикомпьютером
Между алгеброй логики и двоичным
кодированием существует следующая связь :
математический аппарат алгебры
логики очень удобен для описания того как
функционируют
аппаратные
средства
компьютера, поскольку основной системой
счисления в компьютере является двоичная, в
которой используются цифры 1 и 0, а значений
логических переменных
тоже два : “1” и “0”.
3.
Выводы:одни и те же устройства компьютера могут
применяться для обработки и хранения как
числовой информации, представленной в
двоичной системе счисления, так и логических
переменных;
на этапе конструирования аппаратных средств
алгебра логики позволяет значительно упростить
логические функции, описывающие
функционирование схем компьютера, и ,
следовательно, уменьшить число основных узлов
компьютера.
3
4.
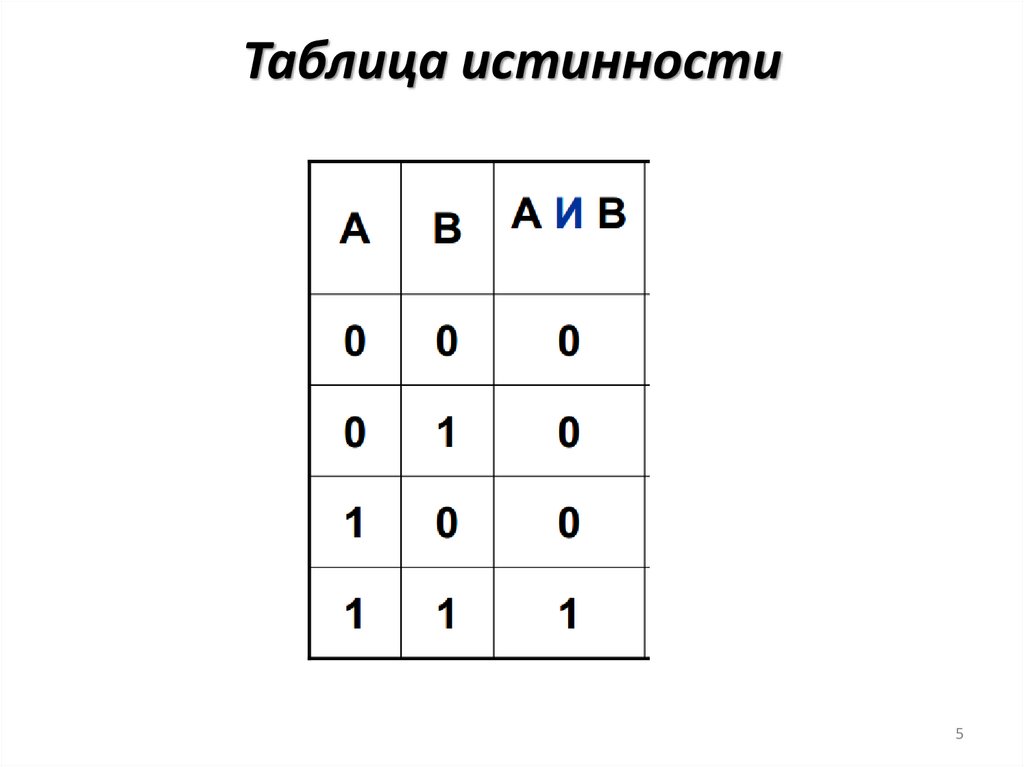
Логические операцииЛогическое умножение (конъюнкция) «И»
A И B или A&B или A ∧ B
A И B истинно тогда и только тогда,
когда оба высказывания A и B истинны.
Примеры:
0 И 0=0 0 И 1=0 1 И 0=0 1 И 1=1
Техническая реализация И два последовательно соединенных
ключа:
4
5.
Таблица истинности5
6.
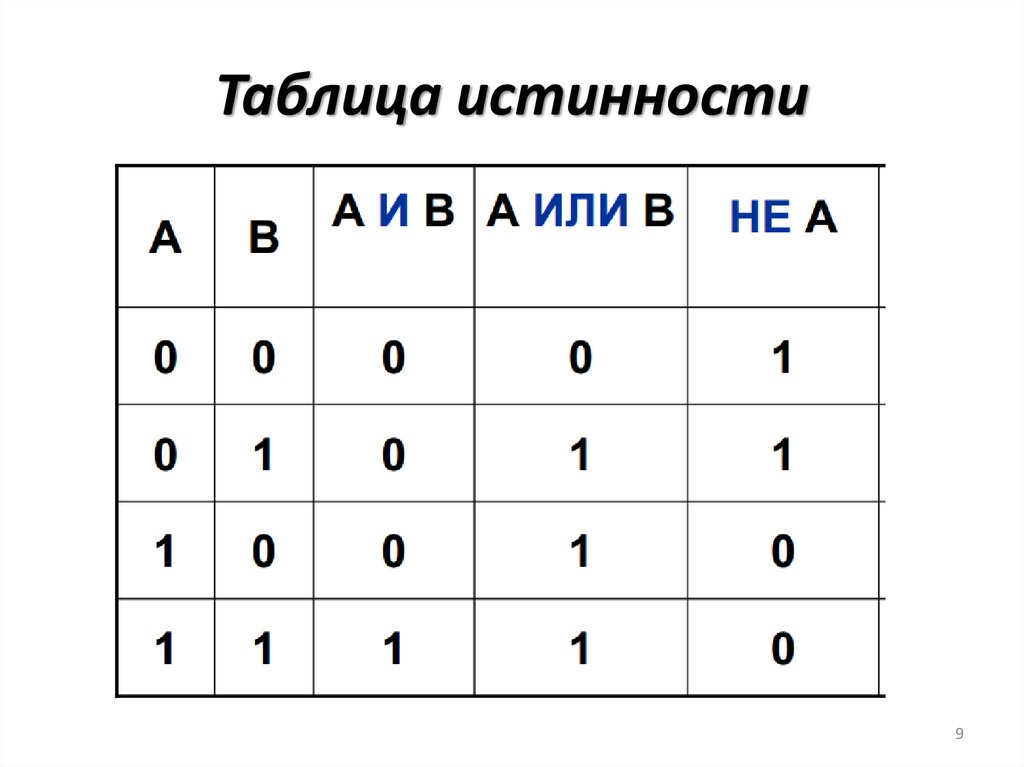
Логическое сложение «ИЛИ»A ИЛИ B или A ∨ B или A+B
A или B ложно тогда и только тогда, когда оба
высказывания A и B ложны.
Примеры:
0 ИЛИ 1=1 1 ИЛИ 0=1 0 ИЛИ 0=0 1 ИЛИ 1=1
Техническая реализация ИЛИ - два параллельно
соединенных ключа:
6
7.
Таблица истинности7
8.
Логическое отрицание (инверсия)Логическое отрицание (инверсия ) «НЕ»
НЕ А или ¬A
делает истинное выражение ложным и,
наоборот, ложное –истинным.
8
9.
Таблица истинности9
10.
Техническая реализация НЕ –при отсутствии электрического тока
через обмотку реле контакты реле
замкнуты,
при протекании достаточного тока через
обмотку реле контакты реле
разомкнуты:
10
11.
Логические операцииЛогическое следование
(импликация) A→B
A→B ложно только тогда,
когда А истинно, а В ложно.
Импликация выражается через
дизъюнкцию и отрицание:
A→B = НЕ A ИЛИ B
11
12.
Таблица истинности12
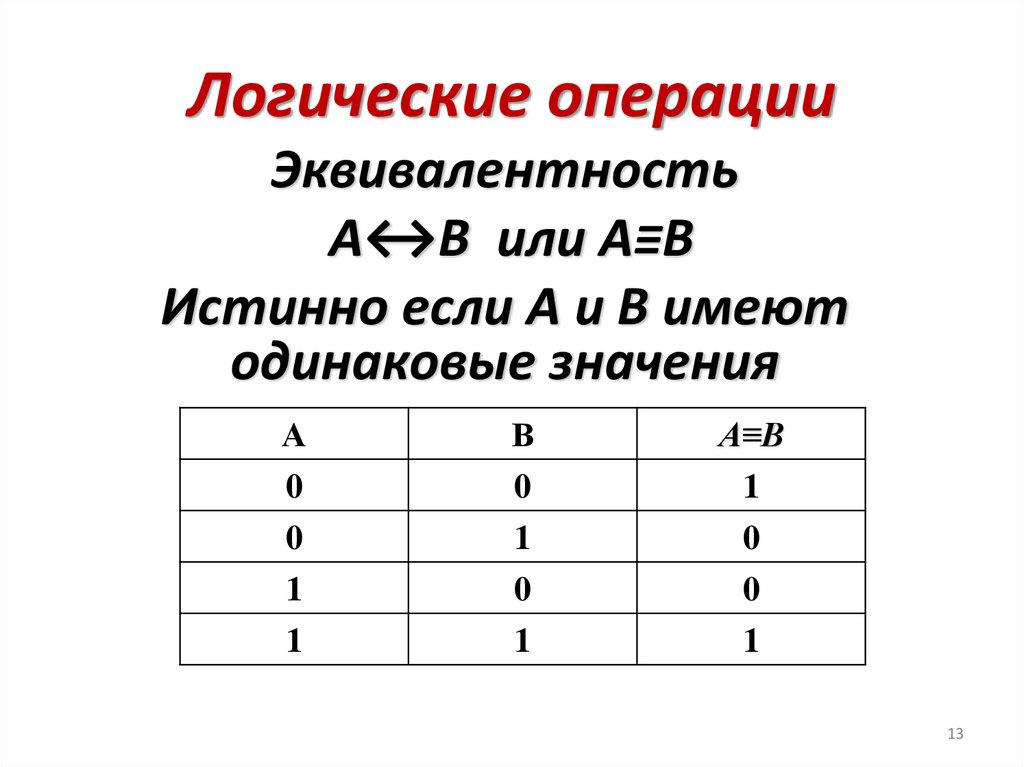
13.
Логические операцииЭквивалентность
A↔B или A≡B
Истинно если А и В имеют
одинаковые значения
А
0
0
1
1
В
0
1
0
1
A≡B
1
0
0
1
13
14.
Приоритет логических операций1) Инверсия НЕ
2) Конъюнкция И
3) Дизъюнкция ИЛИ
4) Импликация →
5) Эквивалентность ↔
14
15.
Законы алгебры логики15
16.
Законы алгебры логики16
17.
Законы алгебры логики17
18.
Задачи1.Для какого значения числа Х, изменяющегося
от 2 до 5, истинно высказывание:
НЕ ((X>3)→ (X>4))?
Решение (способ 1)
18
19.
По таблице истинности импликации видим,что она будет ложной в одном единственном
случае: когда первое высказывание истинно,
а второе ложно.
Первое высказывание (X>3) может быть
истинно только при X=4 или X=5.
Второе высказывание принимает значение
ЛОЖЬ только при X=4.
Ответ: 4
19
20.
Решение (способ 2)Метод последовательной подстановки
1)Х=2 НЕ((2>3)→(2>4))= ¬(0→0)=¬(1)=0
2) X=3 НЕ((3>3)→(3>4))= ¬(0→0)=¬(1)=0
3) X=4 НЕ((4>3)→(4>4))= ¬(1→0)=¬(0)=1
4) X=5 НЕ((5>3)→(5>4))= ¬(1→1)=¬(1)=0
Ответ: 3) 4
20
21.
Логическая функция F задаётся выражением(¬x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w.
x
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
y
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
z
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
w
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
¬x
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
¬y
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
(¬x ∧ ¬y) y ≡ z
1
1
1
1
1
0
1
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
1
0
1
(¬x ∧ ¬y) ∨ (y ≡ z)
1
1
1
1
0
0
1
1
1
1
0
0
0
0
1
1
¬w
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
(¬x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
1
1
1
1
1
0
1
1
1
1
1
0
1
0
1
1
21
22.
1. ¬ X v Y &¬ Z2. ¬ X & ¬ Y v Z
3. X → (Y & ¬ Z)
4. X v ¬ Y ↔ Z
22


















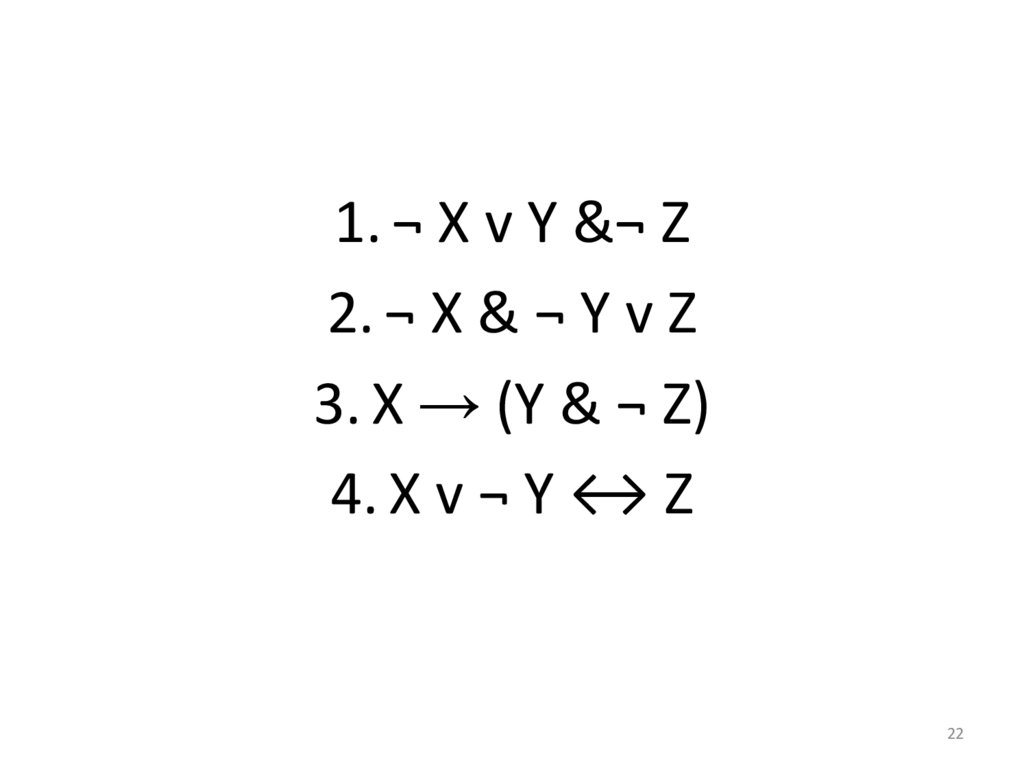
 informatics
informatics








