Высказывания. Законы логики. Элементы теории множеств и математической логики. Лекция №4

1.

Л№4
Высказывания.
Законы логики.
Элементы теории
множеств и
математической логики

2.

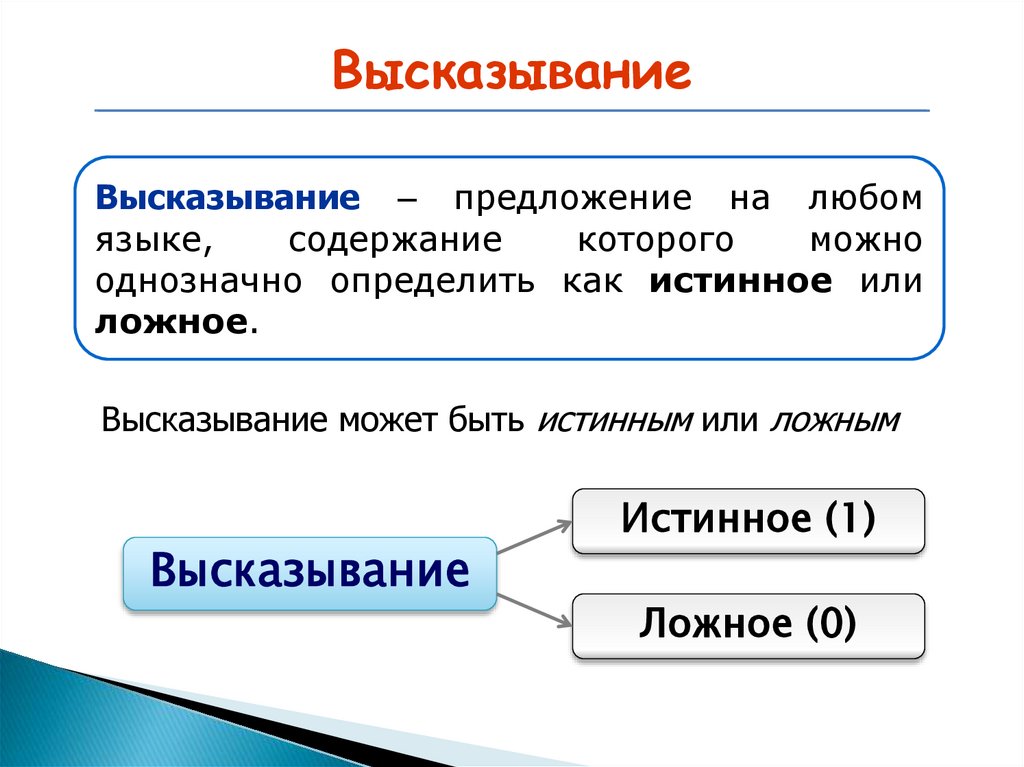
Высказывание
Высказывание – предложение на любом
языке,
содержание
которого
можно
однозначно определить как истинное или
ложное.
Высказывание может быть истинным или ложным
Высказывание
Истинное (1)
Ложное (0)

3.

Алгебра логики
Алгебра логики возникла в середине XIX века в
трудах английского математика Джорджа
Буля. Ее создание представляло собой попытку
решать традиционные логические задачи
алгебраическими методами.
Алгебра логики – это раздел математики,
изучающий высказывания, их логические
значения (истинность или ложность) и
логические операций над ними.

4.

Алгебра логики
Алгебра логики позволяет определять
истинность или ложность составных
высказываний, не вникая в их содержание.
Любое простое высказывание может
принимать значение 0 (ложь) или 1
(истина).
Простое высказывание называют
логическими переменными и обозначают
заглавной латинской буквой – А, В, С и т.д.

5.

Простые и сложные высказывания
Высказывания могут быть простыми или
сложными.
Сложные высказывания состоят из простых
высказываний, соединенных логическими
связками:
и
или
Неверно, что…
Если…, то…

6.

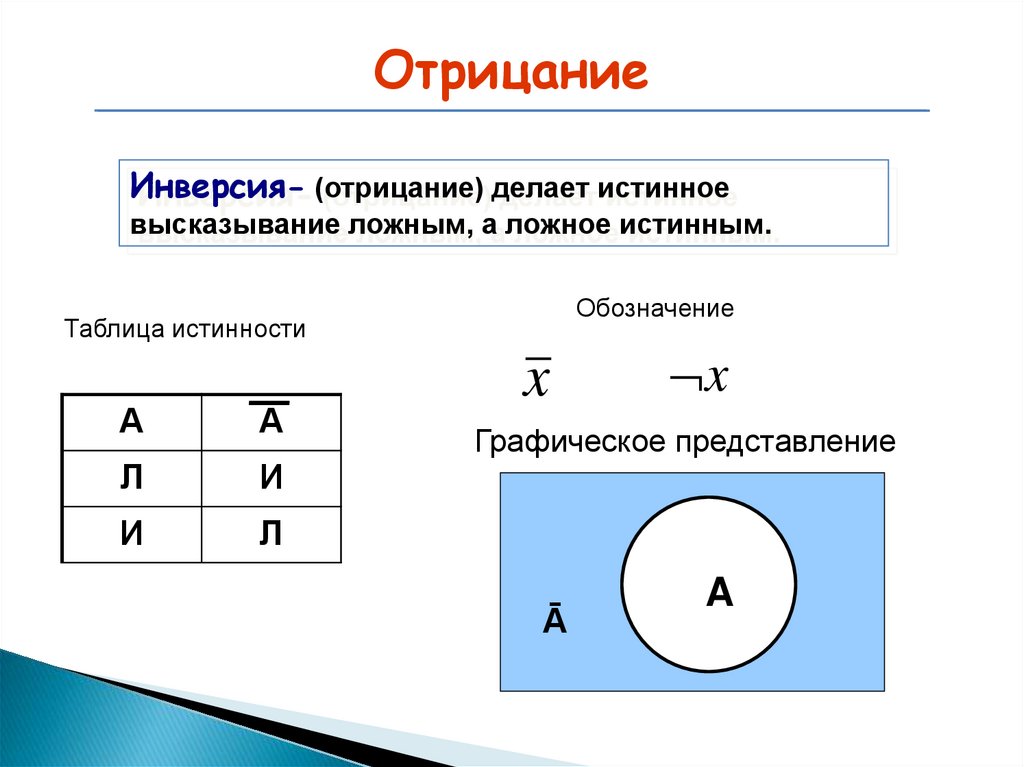
Отрицание
Инверсия- (отрицание) делает истинное
высказывание ложным, а ложное истинным.
Обозначение
Таблица истинности
А
А
Л
И
И
Л
x
x
Графическое представление
Ā
A

7.

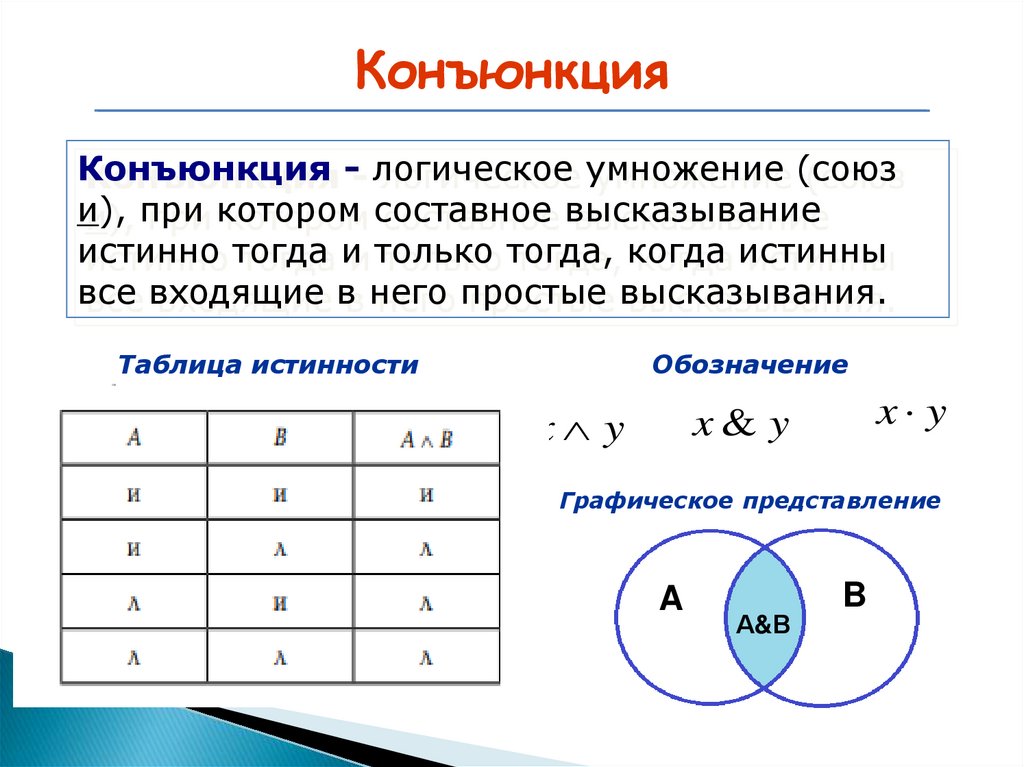
Конъюнкция
Конъюнкция - логическое умножение (союз
и), при котором составное высказывание
истинно тогда и только тогда, когда истинны
все входящие в него простые высказывания.
Таблица истинности
Обозначение
x y
x y
x& y
Графическое представление
A
А&В
B

8.

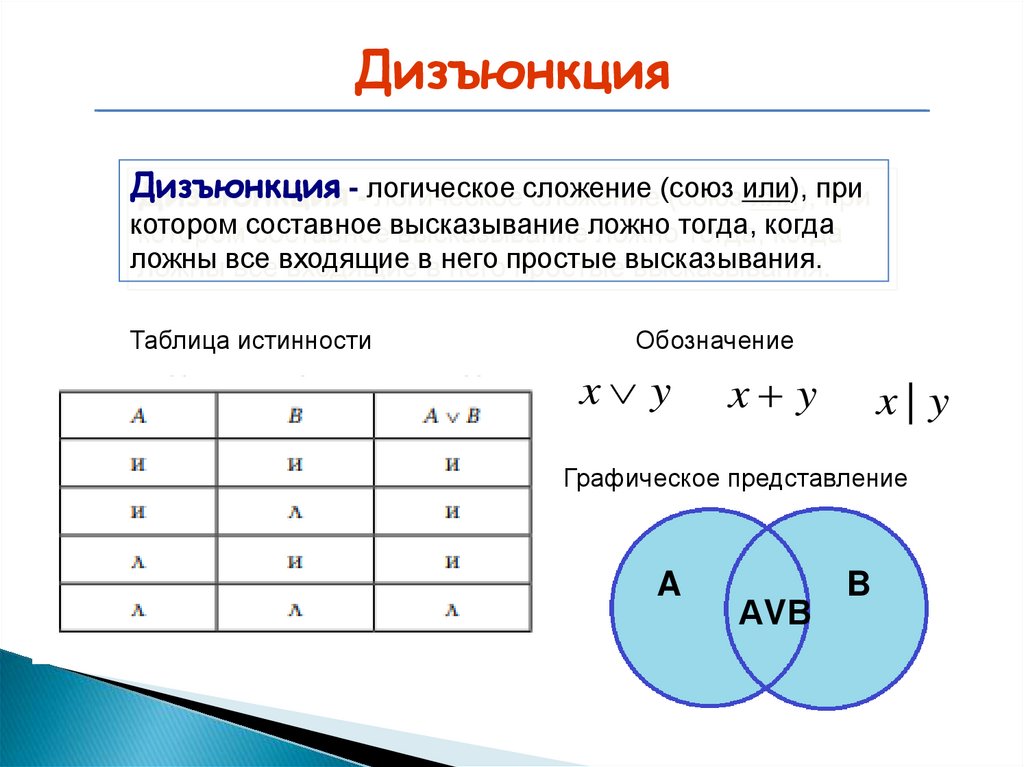
Дизъюнкция
Дизъюнкция - логическое сложение (союз или), при
котором составное высказывание ложно тогда, когда
ложны все входящие в него простые высказывания.
Таблица истинности
Обозначение
x y
x y
x| y
Графическое представление
A
АVВ
B

9.

Импликация
Импликация - (логическое следование если…, то…). Ложно тогда и только тогда,
когда из истинного высказывания следует
ложное.
Таблица истинности
А
В
А→B
л
л
и
л
и
и
и
л
л
и
и
и

10.

А
л
В
л
А→B
и
А ↔B
и
л
и
и
л
и
л
л
л
и
и
и
и

11.

Задание (устно)
Даны два простых высказывания:
А = {2 • 2 = 4},
В = {2 • 2 = 5}.
Какие из высказываний истинны:
а) А; б) В; в) A ^ В; г) A v B ;
д) ¬A;
ж) А ^ ¬В?

12.

Информатика и ИКТ. 9 класс

13.

Задания (устно)
А = «Сейчас нет дождя»
В = «Форточка закрыта»
Составить сложные высказывания
AΛB
AVB
AVB
AΛB
AVB
Пусть А = «Ане нравятся уроки математики», а В =
«Ане нравятся уроки химии». Выразите следующие
формулы на обычном языке:

14.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) A B A
А
В
A
B A
F
л
л
1
0
0
л
и
1
1
1
и
л
0
0
1
и
и
0
0
1

15.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) A B A
А
В
A
B A
F
л
л
и
л
л
л
и
и
и
и
и
л
л
л
и
и
и
л
л
и

16.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
л
л
л
и
и
л
и
и
A B
A
A В
F

17.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
A B
A
A В
F
л
л
л
и
и
л
л
и
и
и
и
и
и
л
и
л
л
л
и
и
и
л
и
и

18.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) (( A B) B) ( A B)
x
А
В
л
л
и
и
л
и
л
и
y
В А В ( А В) В А А В
x y
18

19.

Задание
Составить таблицу истинности
F ( A, B ) (( A B ) B ) ( A B )
x
a
b
л
л
и
и
л
и
л
и
y
В А В ( А В) В А А В
и
и
л
и
и
л
л
и
и
и
и
и
л
л
л
л
и
и
л
и
x y
л
и
л
и
19