Similar presentations:
Призма. Геометрія. 11 клас
1. Призма
Геометрія 11 клас2.
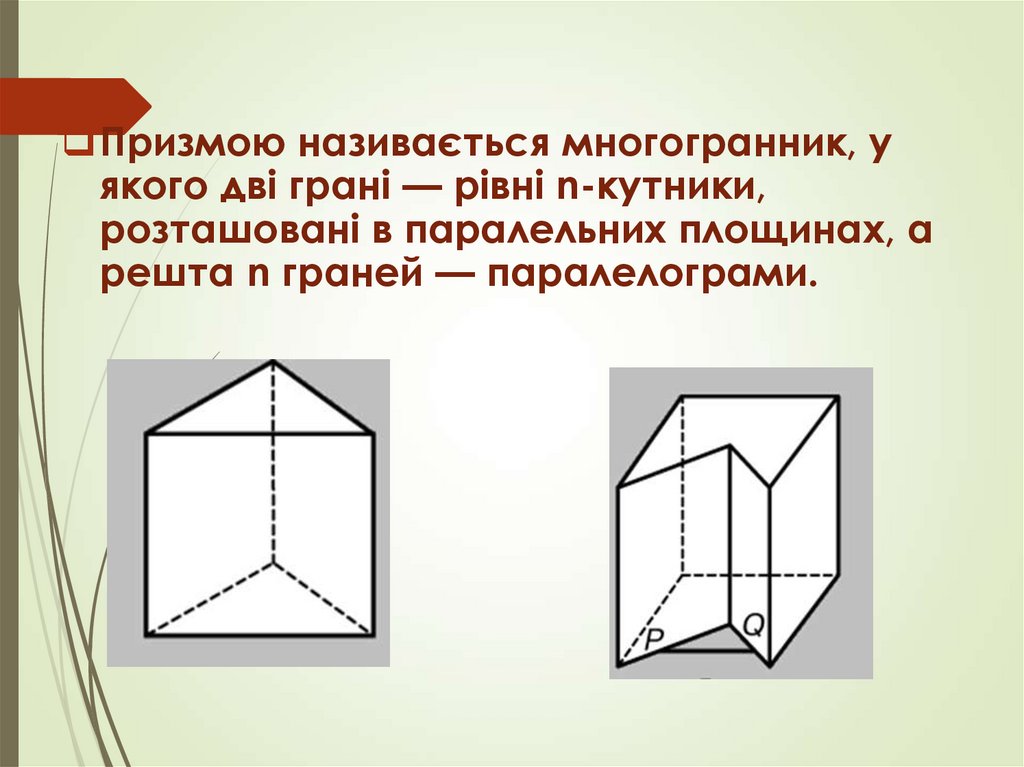
Призмою називається многогранник, уякого дві грані — рівні n-кутники,
розташовані в паралельних площинах, а
решта n граней — паралелограми.
3.
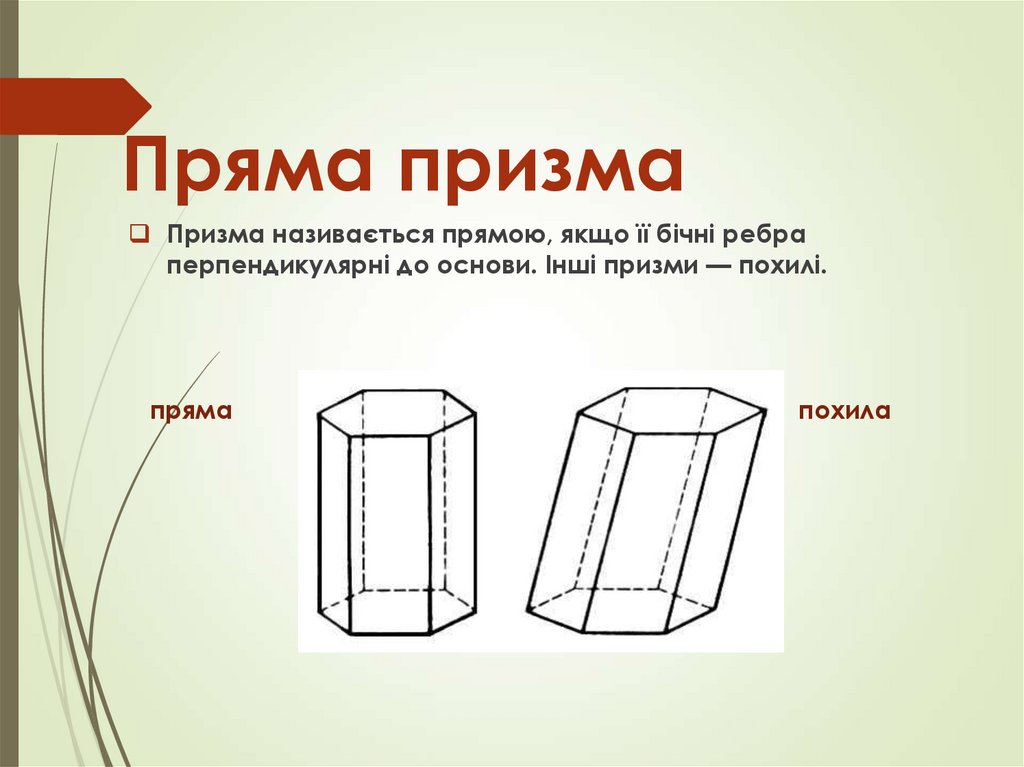
Пряма призмаПризма називається прямою, якщо її бічні ребра
перпендикулярні до основи. Інші призми — похилі.
пряма
похила
4.
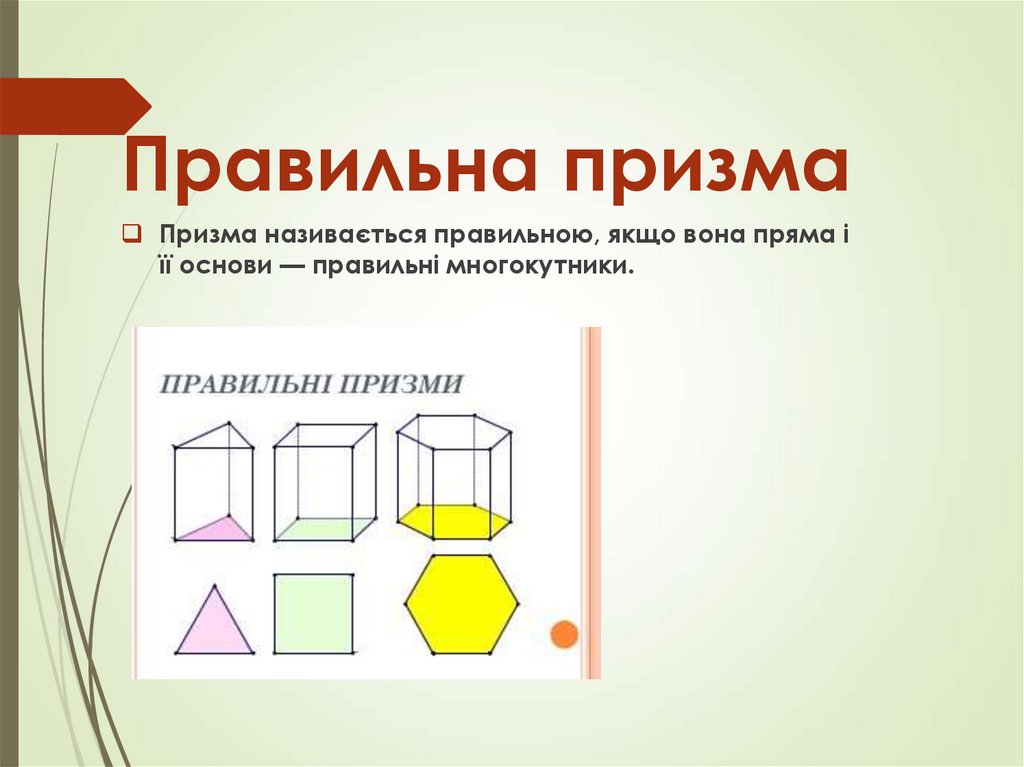
Правильна призмаПризма називається правильною, якщо вона пряма і
її основи — правильні многокутники.
5.
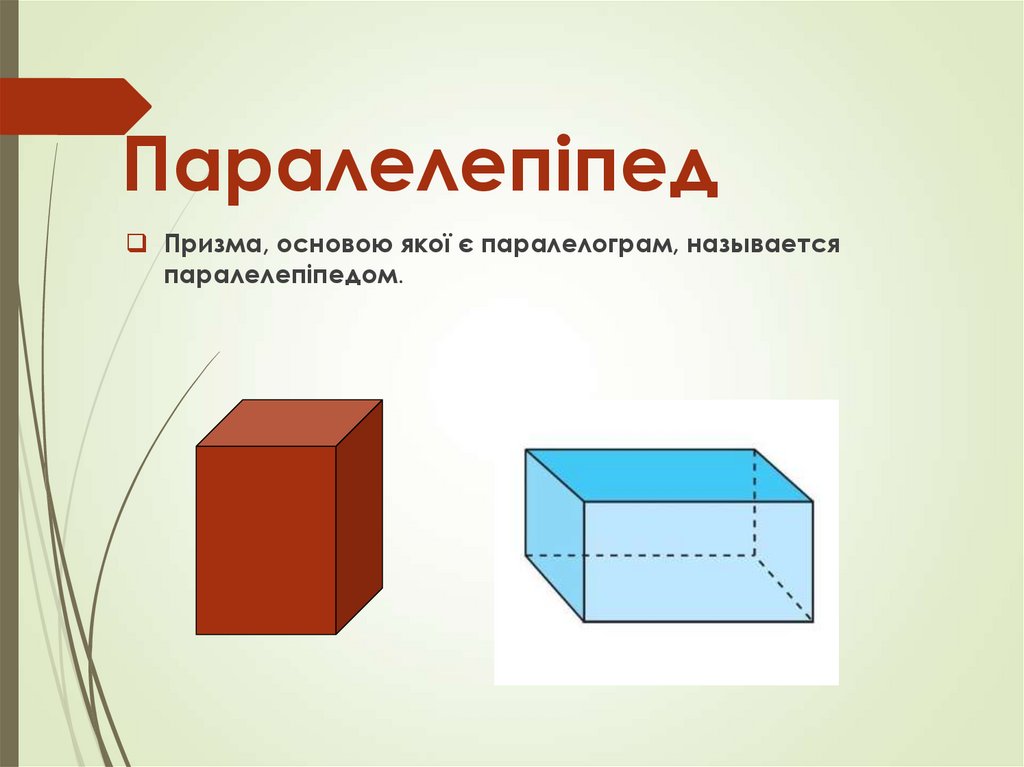
ПаралелепіпедПризма, основою якої є паралелограм, называется
паралелепіпедом.
6. Діагональ призми
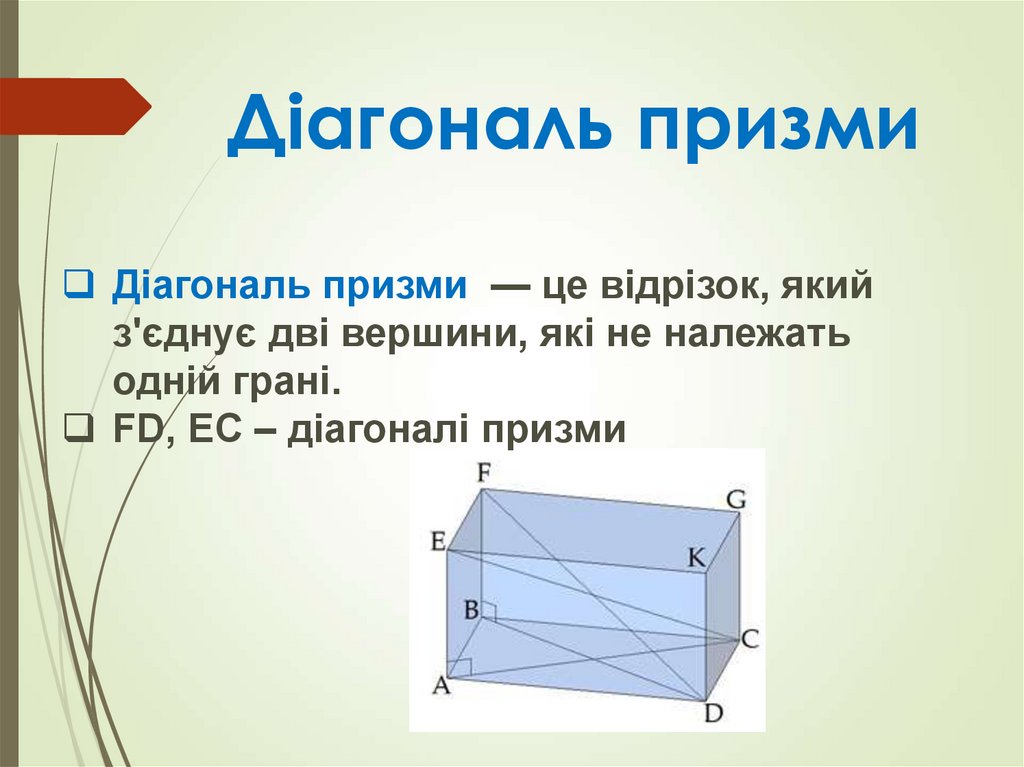
Діагональ призми — це відрізок, якийз'єднує дві вершини, які не належать
одній грані.
FD, EC – діагоналі призми
7. Діагональний переріз призми
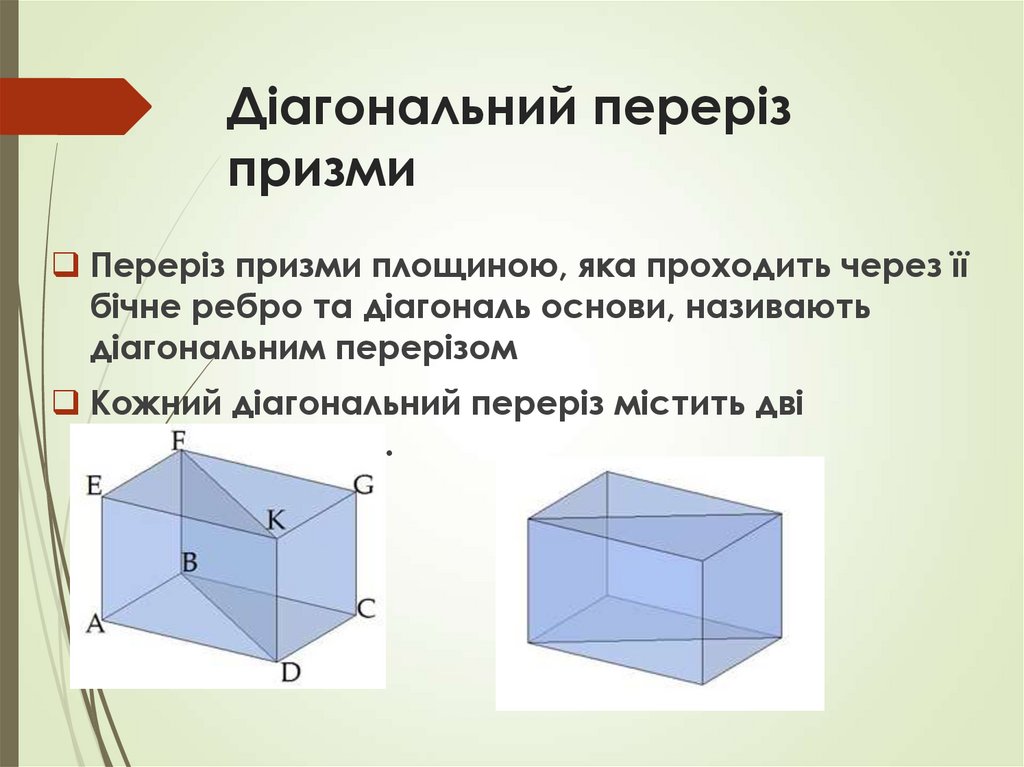
Переріз призми площиною, яка проходить через їїбічне ребро та діагональ основи, називають
діагональним перерізом
Кожний діагональний переріз містить дві
діагоналі призми.
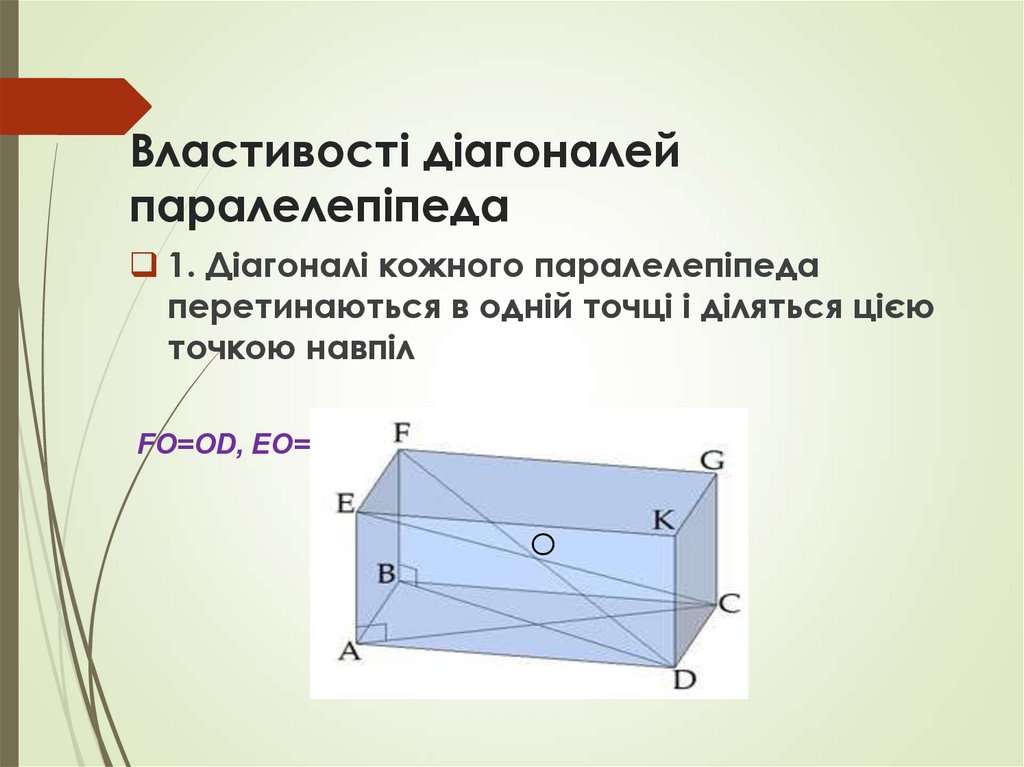
8. Властивості діагоналей паралелепіпеда
1. Діагоналі кожного паралелепіпедаперетинаються в одній точці і діляться цією
точкою навпіл
FO=OD, EO=OC
О
9. Властивості діагоналей паралелепіпеда
10.
Площа поверхніПлощею бічної поверхні призми називають суму
площ усіх її бічних граней. Площа бічної поверхні
прямої призми дорівнює добутку периметра її
основи на висоту:
Sб = P· Н
Площа поверхні призми дорівнює сумі площ її
бічної поверхні та двох основ:
Sп = Sб + 2Sосн
11.
Форму прямокутного паралелепіпедамають цеглини, бруски, контейнери,
ящики для овочів і фруктів, деякі упаковки
продуктів харчування, ліків тощо



 mathematics
mathematics