Similar presentations:
Формальная Логика
1.
Формальная ЛогикаК.Ф.Н. Веденина Нинель Анатольевна
Vedenina.n.a@gmail.com
@Qvenya - telegram
2.
ЛОГОС ΛόΓΟΣ - слово, наука, мысль, смысл, закон, объем.Логика - это наука о мышлении
КАКИЕ НАУКИ ИЗУЧАЮТ МЫШЛЕНИЕ?
ЛОГИКА – наука о правильных формах суждений, о формах
мысли, наука о законах функционирования разума
РАССУЖДЕНИЕ - это последовательность мыслей, в которой из
уже имеющихся мыслей, называемых посылками выводится
новая мысль, которую мы называем заключением.
3.
Как люди добывают знания?1.Итак, некоторые знания о мире мы получаем благодаря органам чувств, – в
данном случае благодаря тому, что одарены зрением и осязанием. Перцептивная
форма.
https://intuit.ru/studies/courses/2191/423/lecture/9638?page=2#:~:text=Процесс%20перцептивного%20мышления%20связан%20с,пространстве%2C%20так%20и%20во%20в
ремени
2.Второй путь – получение новых знаний из уже имеющихся знаний: в этом случае
смотреть следует не на стол, а в книгу (или на экран компьютера). Вот этот второй
путь невозможен без рассуждения. Рассуждения имеют место в самых различных
областях человеческой культуры, в частности, без них немыслимы науки. Логика есть
общий фундамент и основание всех наук.
4.
1)Все люди смертны.2)Сократ – человек.
______________________
Сократ смертен
РАССУЖДЕНИЕ – это получение новых знаний из уже имеющихся
знаний (движение от посылок к выводу).
5.
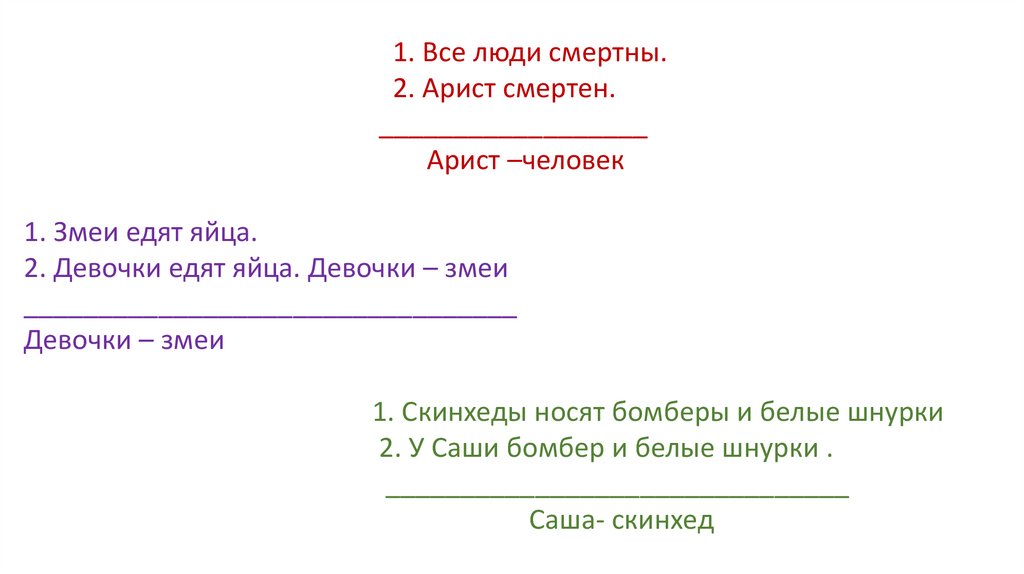
1. Все люди смертны.2. Арист смертен.
__________________
Арист –человек
1. Змеи едят яйца.
2. Девочки едят яйца. Девочки – змеи
_________________________________
Девочки – змеи
1. Скинхеды носят бомберы и белые шнурки
2. У Саши бомбер и белые шнурки .
_______________________________
Саша- скинхед
6.
ЛОГИКА изучает те формы и приемыинтеллектуальной и познавательной
деятельности, которые фиксируются именно в языке.
7.
Если хотим изучать законны ума, то у нас есть двеконцепции:
1.Классическая, идущая от Аристотеля, концепция
разума,
как уникальной способности человеческого существа.
Разум определяет сущность человека. Это не случайный
признак, а сущностный.
Человек есть разумное животное, стремящееся к
счастью, по определению Аристотеля.
Как линейкой измерять линейку.
8.
Если хотим изучать законны ума, то у нас есть две концепции:2. Разум - специфическая, уникальная способность головного мозга.
Человек имеет доступ к разуму через язык и через совокупность социальной
практики.
Таким об. коррелятами деятельности разума является коммуникация.
Коммуникация - это выстроенное человеческое стремление к общему
благу, к взаимодействию.
Это дает нам понимание логического из разума, изнутри.
Человек наблюдает свой собственный разум изнутри самого себя.
Он участвует в опыте, он коррелирует все свои действия через опыт.
9.
Немецкий философ и математик Г.В.Лейбниц (XVIIв.) по правусчитается основоположником математической логики, он первым
применил математические методы для исследования форм
мысли, пытался создать универсальный язык, с помощью которого
споры между людьми можно было бы разрешать посредством
вычисления. Лейбниц полагал, что математику можно свести к
логике (логицизм), а логику считал априорной наукой.
Интенсивное развитие математическая логика получила в работах
Д.Буля,Э.Шрёдера, С.Джевонса, Г.Фреге, Б.Рассела. Сегодня
невозможно представить себе прогресс логического знания без
математических логик. Союз логики и математики оказался
удивительно продуктивным как для логики, так и для математики.
Одним из результатов этого союза стало появление информатики
и вычислительной техники.
10.
Предполагаем, что мы все похожи друг на друга.В этом смысле, разум, одного человека есть
подобие разума другого.
Сознание, чувства, эмоции разные.
То есть сознание -в опыте, опыт разный т.об.
люди разные. Разум одинаковый.
То есть мы рассуждаем логично, потому что мы
просто похожи друг на друга...
11.
Исходя из истинных посылок, можно прийти как кистинным, так и к ложным выводам.
Логика не занимается вопросом об истинности посылок. Это дело
конкретных наук, – физики, химии... Л. Кэрролл. Логическая игра. – М., 1991
1. Ни одна булавка не имеет честолюбивых намерений
2. Ни одна иголка – не булавка.
-------------------------------------------------------------------
Правильное рассуждение – это такое, которое, основываясь на
истинных посылках, приводит к правильному (истинному) выводу.
(Остается, трудный вопрос о том, что такое истина, но его мы
рассмотрим позднее).
12.
Только правильные рассуждения позволяют получатьновые истины из истинных посылок.
Все люди смертны.
Сократ – человек.
S суть P
М суть S
S суть P
1) все рыбы живут в воде
M суть P
2) все щуки живут в воде
_______________________
1)
2)
S суть P
1) Все тигры полосатые
M суть P
2) Все зебры полосатые
_________________________
Все тигры суть зебры
1) Все деревья – зеленые. 2) Тополь – дерево.
_____________________
Тополь зеленый.
________________________
М суть Р
Сократ смертен.
1)Все рыбы плавают. 2) Карась – рыба.
__________________
Карась плавает.
13.
Правильность рассуждения зависит только от его формы и не зависит отсодержания. Именно поэтому она и называется формальной логикой.
Самым общим образом форму рассуждения можно определить как способ
связи входящих в это рассуждение содержательных частей [Ивин А.
А. Логика. – М., 2004, с. 12].
Пусть имеем два утверждения:
1) Все вороны – птицы
2) Все шахматисты – гроссмейстеры
По содержанию эти утверждения различны: первое – истинно, второе –
ложно; в первом идет речь о птицах, во втором – о людях, но форма их
тождественна, строение одинаково и может быть выражено формулой:
Все S суть P.
14.
Для того, чтобы более содержательно, более полнопроиллюстрировать важное понятие формы рассуждения
или логической формы, обратимся к следующей задаче.
Задача №1
Школьный класс состоит из послушных и непослушных
девочек, а также послушных и непослушных мальчиков.
Известно, что число послушных девочек равно числу
непослушных мальчиков.
Кого в классе больше: мальчиков или послушных детей?
15.
Решение. Мальчики делятся на послушных и непослушных:М = П.М. + Н.М. (полное число мальчиков равно количеству
послушных мальчиков сложенному с количеством непослушных
мальчиков).
Воспользуемся теперь условием задачи. Известно, что послушных
девочек столько же, сколько непослушных мальчиков: П.Д.=Н.М.
В уравнение подставим вместо числа непослушных мальчиков
число послушных девочек:
М.= П.М. + Н.М.= П.М. + П.Д.
Однако если сложить число послушных девочек и послушных
мальчиков, то получим число послушных детей; оно равно числу
мальчиков.
Ответ: мальчиков столько же, сколько послушных детей.
16.
Внимание! Проверьте себя: что можно сказать о количестве девочек вклассе?
Нетрудно сообразить, что девочек столько же, сколько непослушных
детей.
Это можно показать строго математически:
Д = П.Д. + Н.Д. (полное число девочек равно числу послушных девочек,
сложенному с числом непослушных девочек). Однако число послушных
девочек равно числу непослушных мальчиков: П.Д.=Н.М.
Тогда Д= П.Д.+Н.Д.= Н.М.+ Н.Д.
Если сложить число непослушных мальчиков и непослушных девочек,
то получим число непослушных детей.
Можно не прибегать к формулам, если сообразить, что, каково бы ни
было число детей в классе, оно не меняется в зависимости от способа
деления!
17.
Задача №2В гостинице для животных живут черные и белые собаки, а также
черные и белые коты. Известно, что белых собак в точности
столько же, сколько черных котов. Кого в гостинице больше –
котов или белых животных?
Решение.
Ответ:
18.
Практическое заданиеСоставить еще одну задачу по этой схеме.
(Например: В подушечку для шитья вкололи
некоторое число честолюбивых и смиренных иголок,
а также некоторое число честолюбивых и смиренных
булавок. Известно, что честолюбивых иголок ровно
столько же, сколько смиренных булавок.
Спрашивается, чего больше – иголок или смиренных
швейных принадлежностей?)
19.
Форма рассуждения - способ связи входящих в эторассуждение содержательных частей.
форму рассуждения можно отделить от его содержания
Выдающийся физик ХХ в., нобелевский лауреат Э. Вигнер
называет один из разделов своей знаменитой книги «Этюды о
симметрии» так: «Непостижимая ффективность математики
в естественных науках» [Вигнер Е. Этюды о симметрии. – М.,
1971, с. 182 – 197].
Эпиграфом к своей работе Вигнер ставит слова выдающегося
логика XIX в. Ч. С. Пирса: «…по-видимому, здесь есть какая-то
тайна, которую нам еще предстоит раскрыть».
20.
Отчетливое определение понятия натурального числа на основепонятия множества (совокупности предметов) было дано в 70-х
гг. XIX в. в работах великого математика, создателя теории
множеств Георга Кантора.
Понятие равномощности совокупностей - две совокупности
называются равномощными, если составляющие их предметы могут
быть сопоставлены по одному. Множество трех мальчиков и
множество трех котов равномощны (каждому мальчику можно дать
в руки по коту).
Затем число предметов, составляющих данную совокупность,
определяется как то общее, что имеет данная совокупность и всякая
другая, равномощная ей совокупность предметов, независимо от
всяких качественных особенностей этих предметов



















 philosophy
philosophy








