Механические колебания

1.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

2.

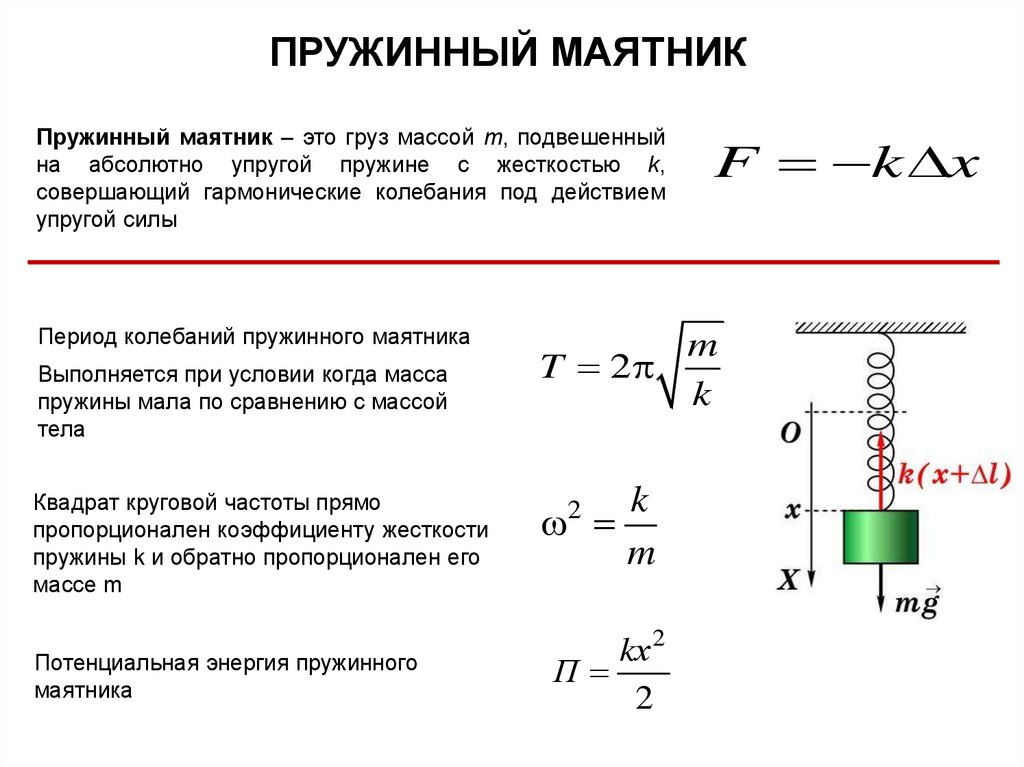
ПРУЖИННЫЙ МАЯТНИК
Пружинный маятник – это груз массой m, подвешенный
на абсолютно упругой пружине с жесткостью k,
совершающий гармонические колебания под действием
упругой силы
Период колебаний пружинного маятника
Выполняется при условии когда масса
пружины мала по сравнению с массой
тела
Квадрат круговой частоты прямо
пропорционален коэффициенту жесткости
пружины k и обратно пропорционален его
массе m
Потенциальная энергия пружинного
маятника
F k x
m
T 2
k
k
m
2
kх 2
П
2

3.

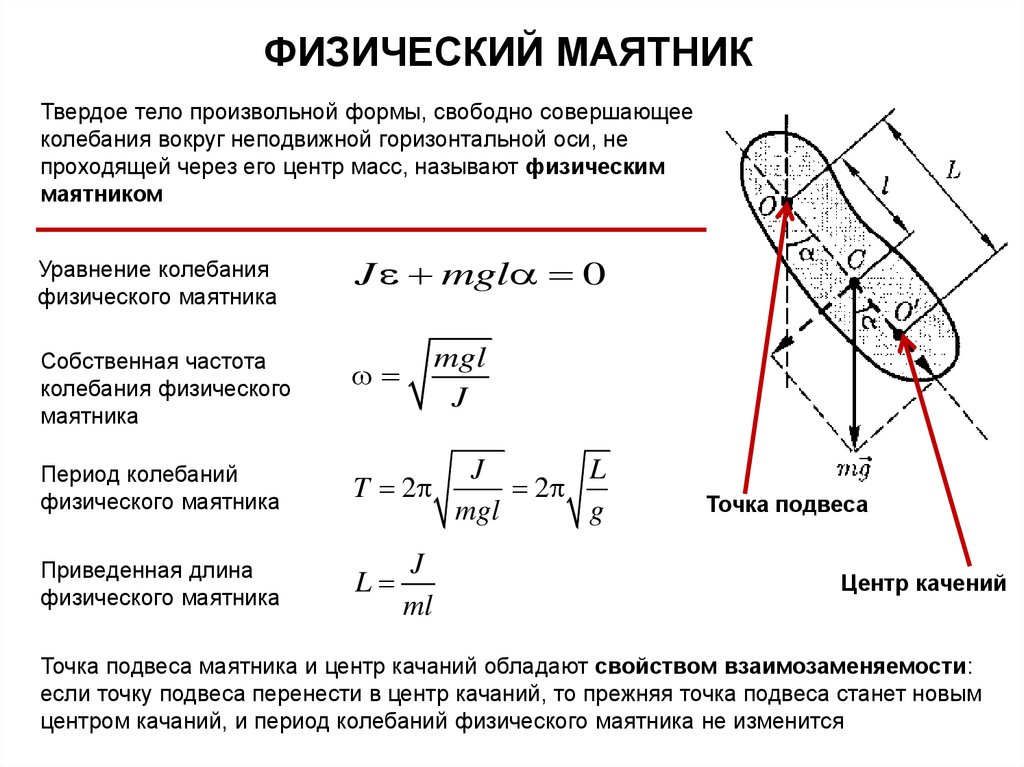
ФИЗИЧЕСКИЙ МАЯТНИК
Твердое тело произвольной формы, свободно совершающее
колебания вокруг неподвижной горизонтальной оси, не
проходящей через его центр масс, называют физическим
маятником
Уравнение колебания
физического маятника
J mgl 0
Собственная частота
колебания физического
маятника
Период колебаний
физического маятника
T 2
Приведенная длина
физического маятника
L
mgl
J
J
ml
J
L
2
mgl
g
Точка подвеса
Центр качений
Точка подвеса маятника и центр качаний обладают свойством взаимозаменяемости:
если точку подвеса перенести в центр качаний, то прежняя точка подвеса станет новым
центром качаний, и период колебаний физического маятника не изменится

4.

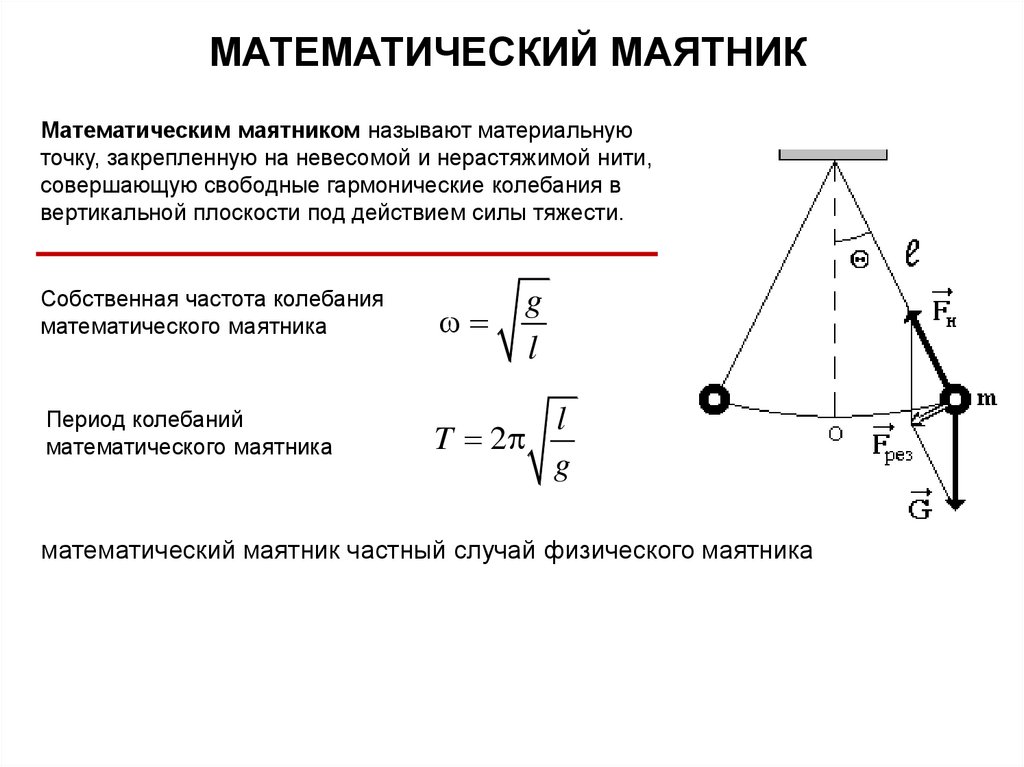
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Математическим маятником называют материальную
точку, закрепленную на невесомой и нерастяжимой нити,
совершающую свободные гармонические колебания в
вертикальной плоскости под действием силы тяжести.
Собственная частота колебания
математического маятника
Период колебаний
математического маятника
l
T 2
g
g
l
математический маятник частный случай физического маятника

5.

БАЛЛИСТИЧЕСКИЙ МАЯТНИК
Баллистический маятник представляет собой тяжелое
тело, подвешенное на двойных нитях
m m M 1
закон сохранения
импульса
1
m M 12 M m gh
2
закон сохранения
механической энергии
AK 2 S 2 l 2 - l - h 2lh h2
S 2 Так как l>>h, то 2
h
S 2lh
2l
2
+mS g
Mm
l
скорости пули
перед ударом

6.

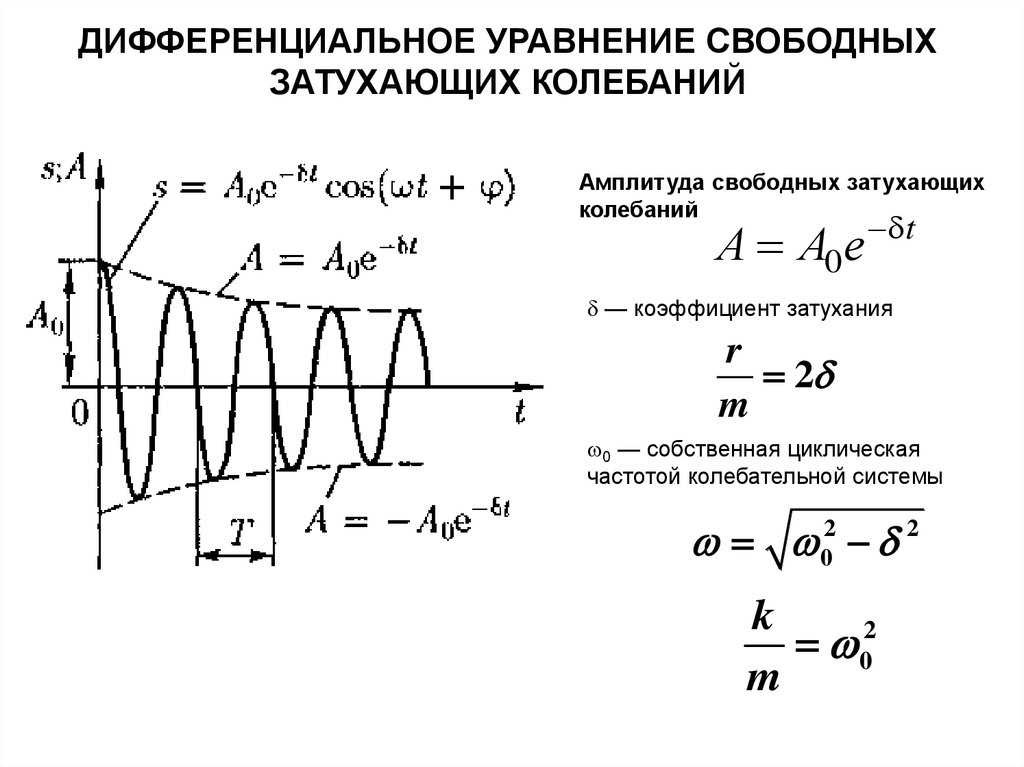
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ
ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии с
течением времени уменьшаются.
Энергия механических колебаний расходуется на работу против сил трения и амплитуда
колебаний уменьшается
Сила трения (или сопротивления)
Fтр r
r – коэффициент сопротивления,
– скорость движения
Дифференциальное уравнение свободных затухающих колебаний
d 2x
dx
2
2 0 x 0
2
dt
dt
х — колеблющаяся величина, описывающая тот или иной физический процесс,
=const — коэффициент затухания,
0 — собственная циклическая частотой колебательной системы

7.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ
ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Амплитуда свободных затухающих
колебаний
А А0 е t
— коэффициент затухания
r
2
m
0 — собственная циклическая
частотой колебательной системы
02 2
k
02
m

8.

ХАРАКТЕРИСТИКИ СВОБОДНЫХ ЗАТУХАЮЩИХ
КОЛЕБАНИЙ
Промежуток времени = 1/ , в течение которого амплитуда затухающих колебаний
уменьшается в е = 2.7 раз, называется временем релаксации.
Период затухающих колебаний
равен (условно)
Циклическая частота
затухающих колебаний
2
T
2 2
2
2 2
k r
m 2m
2
Собственная частота
пружинного
маятника
k
m
Декремент затухания
Коэффициент затухания
А(t )
e T
A(t T )
r
2m
А(t), A(t+T) — амплитуды двух
последовательных колебаний,
соответствующих моментам времени,
отличающимся на период
r — коэффициент сопротивления