Равномерное и неравномерное кодирование. Перебор слов и системы счисления

1. Равномерное и неравномерное кодирование

Дома:
1) §5, основные понятия,
степени 2, формулы
2) Решить задачи
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

2. 8. Перебор слов и системы счисления

2
8. Перебор слов и системы
счисления
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 4 минуты.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

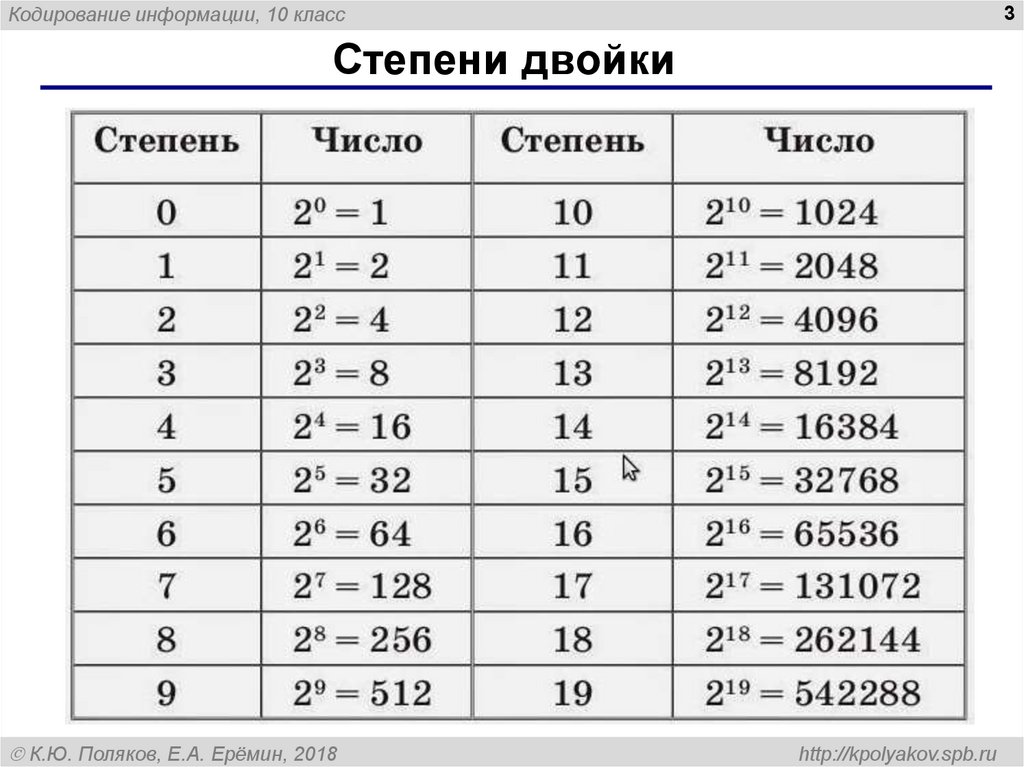
3. Степени двойки

Кодирование информации, 10 класс
3
Степени двойки
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

4. Вспомним известное

Кодирование информации, 10 класс
4
Вспомним известное
Алфавит — это набор знаков, который
используется в языке.
Мощность алфавита — это количество знаков в
алфавите.
Равномерный код — это код, в котором все
кодовые слова имеют одинаковую длину.
А
000
Г
010
К.Ю. Поляков, Е.А. Ерёмин, 2018
Р
100
кодовое слово
http://kpolyakov.spb.ru

5. Вспомним известное

Кодирование информации, 10 класс
5
Вспомним известное
Неравномерный код — это код, в котором
кодовые слова имеют различную длину.
А
0
Г
1
Р
10
Двоичное кодирование — это кодирование с
помощью двух знаков.
1 бит — это одна двоичная цифра (один знак
сообщения, записанного в двоичном коде).
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
0
0
1
0
http://kpolyakov.spb.ru

6. Количество возможных сообщений

Кодирование информации, 10 класс
6
Количество возможных сообщений
Если алфавит языка состоит из M символов
(имеет мощность M), количество различных
сообщений длиной L знаков равно
N=ML
Для двоичного кода: N = 2L
27
Сколько
• возможных 7-битовых двоичных кодов?
• возможных 5-буквеных слов в русском
335
языке?
• возможных 3-буквеных слов в английском
языке?
263
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

7. Количество возможных сообщений

Кодирование информации, 10 класс
7
Количество возможных сообщений
Сколько
• различных чисел можно закодировать в
8-битовой ячейке?
28
• различных чисел можно закодировать в
8-разрядной ячейке троичного компьютера
(-1, 0, 1)?
38
10
• сколько битов нужно выделить для
хранения номера спортсмена от 1 до 1000?
512 = 29 < 1000 210 = 1024
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

8. Правило умножения

Кодирование информации, 10 класс
8
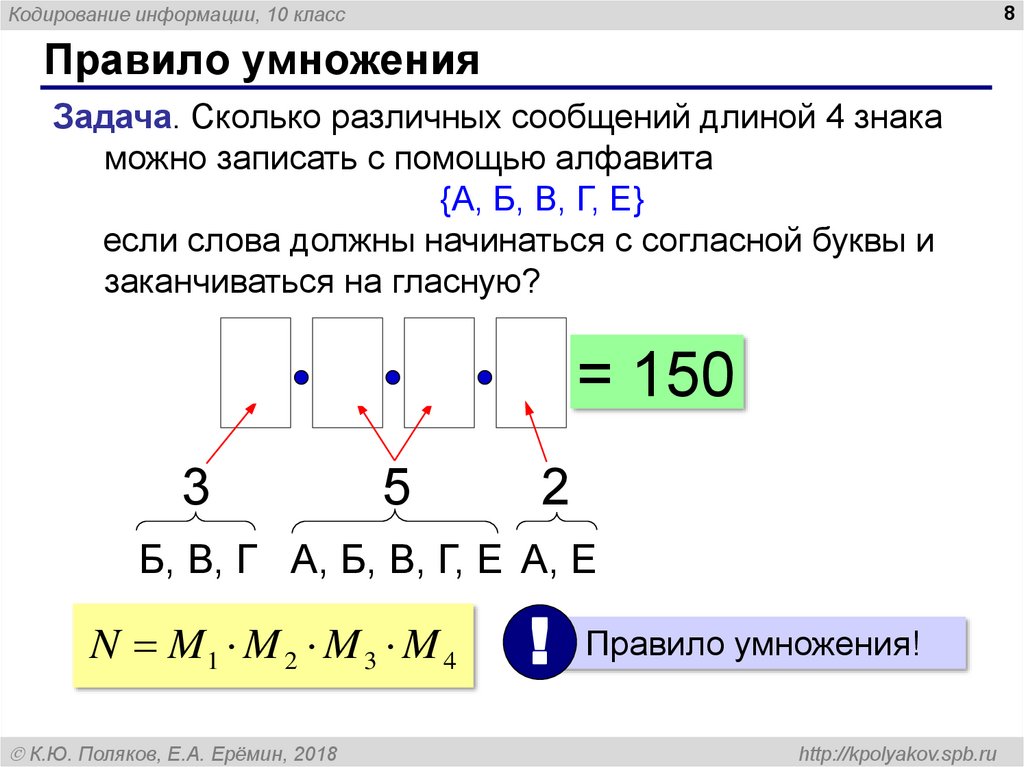
Правило умножения
Задача. Сколько различных сообщений длиной 4 знака
можно записать с помощью алфавита
{А, Б, В, Г, Е}
если слова должны начинаться с согласной буквы и
заканчиваться на гласную?
3 5 5 2 = 150
3
5
2
Б, В, Г А, Б, В, Г, Е А, Е
N M1 M 2 M 3 M 4
К.Ю. Поляков, Е.А. Ерёмин, 2018
! Правило умножения!
http://kpolyakov.spb.ru

9. Правило умножения

Кодирование информации, 10 класс
9
Правило умножения
Если в сообщении длиной L на позиции i может
стоять один из Mi символов, количество
различных сообщений равно
N = M1 M2 … ML
Задача. Сколько существует различных
сообщений длины 5 в алфавите {A, B, C, Х},
если буква «Х» может появляться только на
первом или на последнем месте?
4
3
3
3
4
4 ∙ 3 ∙ 3 ∙ 3 ∙ 4 = 432
M1 M2 M3 M4 M5
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

10. Правило умножения

Кодирование информации, 10 класс
10
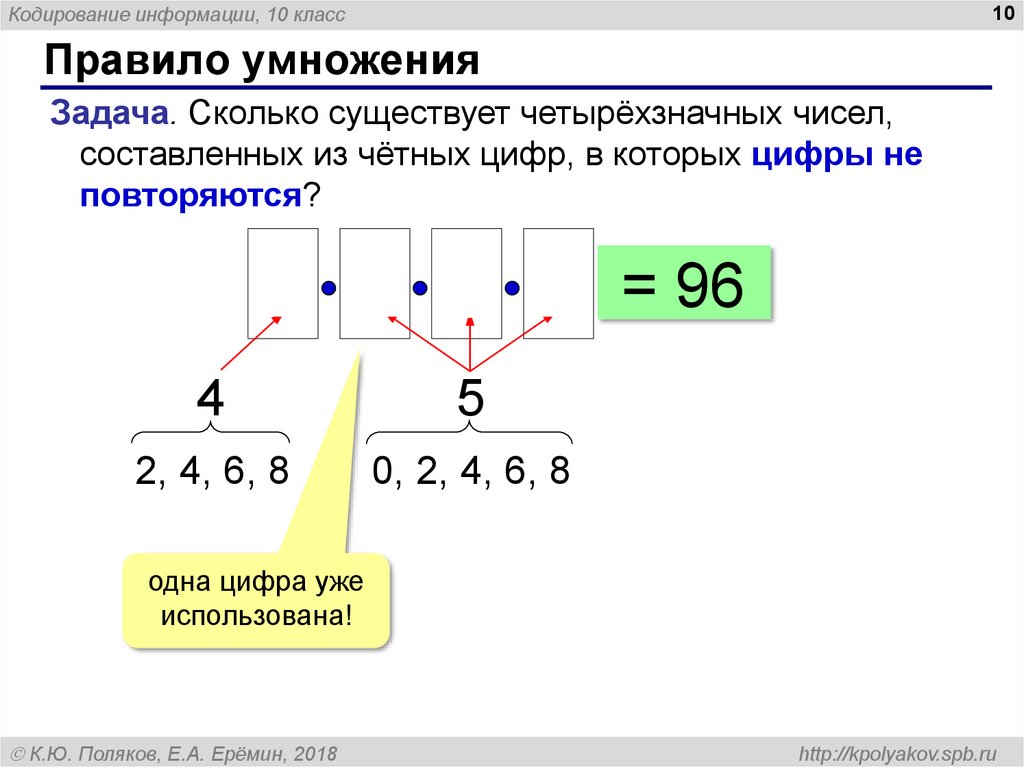
Правило умножения
Задача. Сколько существует четырёхзначных чисел,
составленных из чётных цифр, в которых цифры не
повторяются?
4 4 3 2 = 96
4
5
2, 4, 6, 8
0, 2, 4, 6, 8
одна цифра уже
использована!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

11. Правило умножения

Кодирование информации, 10 класс
11
Правило умножения
Задача. Сколько существует 5-значных
десятичных чисел, все цифры в которых
различны?
9
9
8
7
6
9 ∙ 9 ∙ 8 ∙ 7 ∙ 6 = 27216
M1 M2 M3 M4 M5
Не может быть 0!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

12. Неравномерные коды

Кодирование информации, 10 класс
12
Неравномерные коды
• можно уменьшить длину закодированного
сообщения
Равномерный код:
12 бит
А
00
Г
01
Р
10
ГАГАРА → 010001001000
Неравномерный код:
А
0
Г
01
Р
10
9 бит
ГАГАРА → 010010100
• не всегда однозначно декодируется
→ 010010100 ГАГАРА
010010100
→ 010010100 АРАРРА
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

13. Правило сложения

Кодирование информации, 10 класс
13
Правило сложения
Задача. Сколько существует двоичных кодов
длиной от 2 до 5 битов?
L = 2:
L = 4:
N2 = 22 = 4
N4 = 24 = 16
L = 3:
L = 5:
N3 = 23 = 8
N5 = 25 = 32
N = 4 + 8 + 16 + 32 = 60
N = N2 + N3 + N4 + N5
К.Ю. Поляков, Е.А. Ерёмин, 2018
! Правило сложения!
http://kpolyakov.spb.ru

14. Правила умножения и сложения

Кодирование информации, 10 класс
14
Правила умножения и сложения
Задача. Сколько существует различных
3-буквенных слов в алфавите {К, Р, О, Т}, в
которых буква К встречается ровно 1 раз?
К
*
*
1
3
3
1∙3∙3=9
*
К
*
3∙1∙3=9
*
*
К
3∙3∙1=9
К.Ю. Поляков, Е.А. Ерёмин, 2018
9 + 9 + 9 = 27
http://kpolyakov.spb.ru

15. Алгоритм

Кодирование информации, 10 класс
15
Алгоритм
Сколько слов определенной длины существует
1)Если нет ограничений: возводим количество букв (M) в
степень количества букв в слове (L)!
2) Если есть ограничения: четко записываем, на какое
место сколько вариантов возможно:
• Например! На первое место 5 букв, на второе 5 букв, а
на третье 4!
• И далее перемножим 5*5*4 и получим ответ!
3) Если нужно найти вариант, когда одна буква появляется
в слове ровно N раз, то расписываем все варианты или
просто умножаем один такой вариант на количество
комбинаций. Итоговое число будет ответом!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

16. Задача

Кодирование информации, 10 класс
16
Задача
Вася составляет 4-буквенные слова, в которых есть только
буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1
раз. Каждая из других допустимых букв может встречаться в слове
любое количество раз или не встречаться совсем.
Сколько существует таких слов, которые может написать Вася?
Решение:
• Так как по условию буква Е встретится хотя бы 1 раз, значит, можно
утверждать, что не может быть такого, чтобы буква Е не
встретилась бы ни одного раза.
• Таким образом, рассчитаем случай, когда буква Е встречается
все 4 раза (т.е. все случаи) и отнимем от результата невозможный
случай - когда буква Е не встретится ни одного раза:
1. Буква Е используется 4 раза (т.е. на всех позициях): 44 = 256
2. Буква Е не используется совсем (т.е. только 3 буквы): 34 = 81
3. 256 – 81 = 175
Ответ: 175
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

17. Алгоритм

Кодирование информации, 10 класс
17
Алгоритм
Буква должна встречаться хотя бы 1 раз
1) Необходимо посчитать сначала все комбинации, когда
буква встречается и не встречается вообще: чаще всего
это количество букв (M) в степени количества символов
в слове (L)!
2) Нужно вычесть из общего количества количество
вариантов без букв
3) Другой вариант: перебирать все варианты, когда буква
встречается 1 раз, когда 2 и т. д. и потом все сложить!
Ответ будет такой же!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

18. ДЗ (профиль)

Кодирование информации, 10 класс
18
ДЗ (профиль)
• https://www.kompege.ru/
• https://education.yandex.ru/ege/go
• Ссылка-приглашение:
https://education.yandex.ru/teacherege/join?token=gAAAAABm2b1ewMsLMcDiyxBXsaEpmr9isLcBidkzXd7x5jJekKt
p0ZibmMoi7wptq2Hk_KvV8LQQDUrNivci6JEdWKd_RWFN1PVqWAPh53CsdbX
FuK2JAAzLmYcAt51RL2n_aNzvRISFzXqL8O2H2Lp72HLSS6tjAH6IXVoHp2jdEi
0u3T5K6q1bUUeE0jto2r3--w6gUol5IxsuvN7ADTfON03dTU79g==
• Ссылка на задание: https://ya.cc/5NT4LN
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru