Шар и сфера в заданиях ЕГЭ

1.

Шар и сфера
в заданиях
ЕГЭ

2. Задача №1

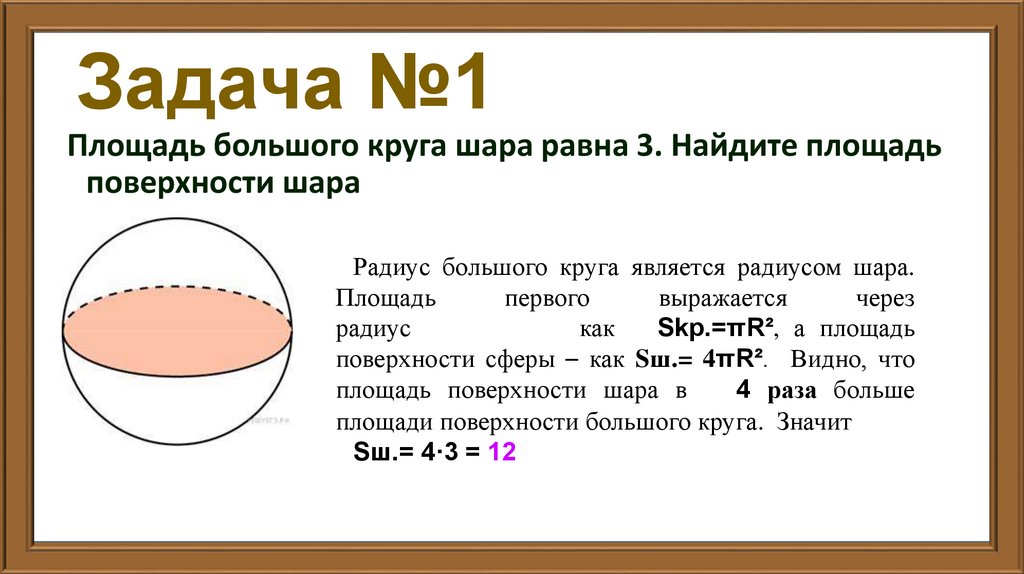
Площадь большого круга шара равна 3. Найдите площадь
поверхности шара
Радиус большого круга является радиусом шара.
Площадь
первого
выражается
через
радиус
как
Skp.=πR², а площадь
поверхности сферы – как Sш.= 4πR². Видно, что
площадь поверхности шара в
4 раза больше
площади поверхности большого круга. Значит
Sш.= 4·3 = 12

3. Задача №2

Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 2 раза?
Площадь
поверхности
шара
выражается
через
его
радиус
формулой Sш.= 4πR², поэтому при
увеличении радиуса вдвое площадь
увеличится в 22 = 4 раза.

4. Задача №3

Даны два шара. Диаметр первого шара в 8 раз больше
диаметра второго. Во сколько раз площадь поверхности
первого шара больше площади поверхности второго?
S1:S2= R1²: R2²= (R1/R2)²=(d1/d2)²=8²=64

5. Задача №4

Даны два шара с радиусами 8 и 4. Во сколько раз площадь
поверхности первого шара больше площади поверхности
второго?
Решение. Т.к. Площадь поверхности шара вычисляется по
формуле: S = 4π·r², то
1) Найдём площадь поверхности первого шара: 256π
2) Найдём площадь поверхности второго шара: 64π
3) Найдём отношение площадей:
256π : 64π = 4

6. Задача №5

Радиусы двух шаров равны 6, 8. Найдите радиус шара,
площадь поверхности которого равна сумме площадей их
поверхностей.
Из условия S3=S1+S2 и S = 4π·r²
найдём
4 R 4 R 4 R
2
3
2
1
2
2
R3 R R 36 64 10
2
1
2
2

7. Касательная плоскость к сфере

8. Повторение «Взаимное расположение сферы и плоскости»

Пусть R - радиус, d = OA - расстояние от
центра шара до плоскости.
1) d > R: сфера и плоскость не имеют
общих точек.

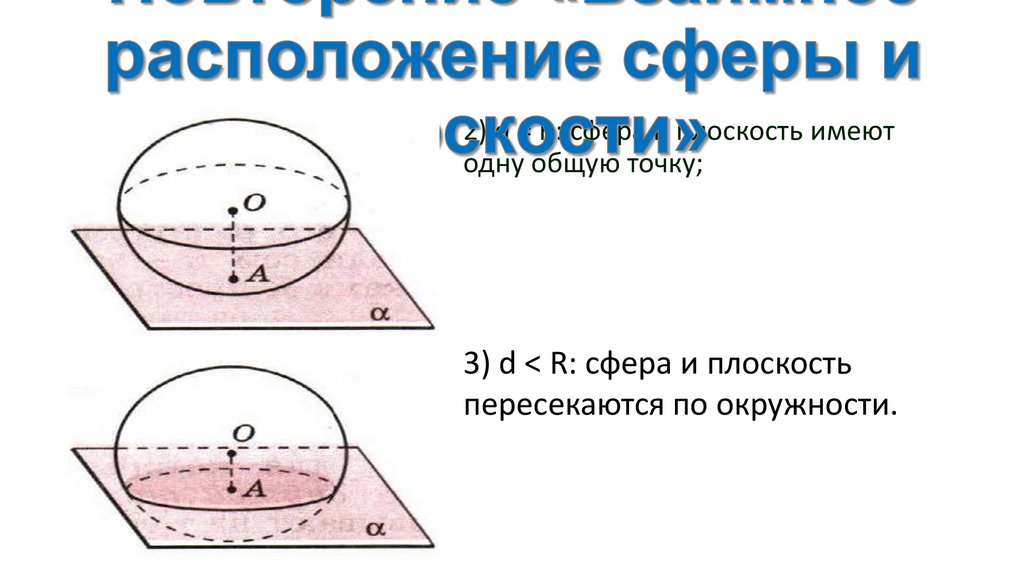
9. Повторение «Взаимное расположение сферы и плоскости»

2) d = R: сфера и плоскость имеют
одну общую точку;
3) d < R: сфера и плоскость
пересекаются по окружности.

10. Касательная плоскость к сфере

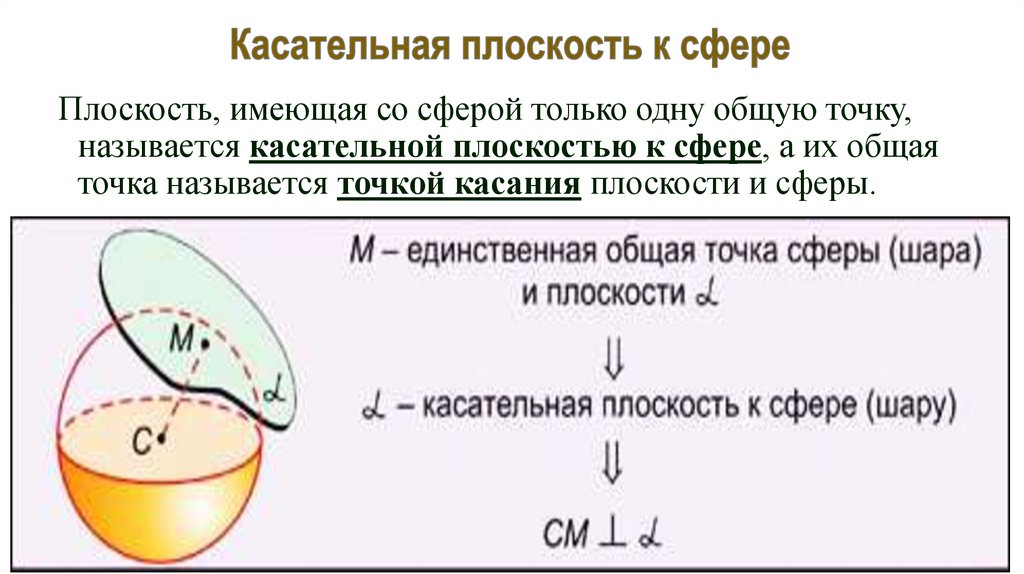
Плоскость, имеющая со сферой только одну общую точку,
называется касательной плоскостью к сфере, а их общая
точка называется точкой касания плоскости и сферы.

11. Касательная

Свойство касательной к окружности Свойство касательной плоскости (к сфере)
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
Если прямая касается окружности ,
то она перпендикулярна радиусу,
проведённому в точку касания.
Если…, то…

12. Касательная

Свойство касательной к окружности
Свойство касательной плоскости сферы
Касательная к окружности
Касательная плоскость сферы
перпендикулярна к радиусу,
перпендикулярна радиусу,
проведённому в точку касания. проведённому в точку касания.
Если прямая касается
Если плоскость касается сферы, то
окружности , то она
она перпендикулярна радиусу,
перпендикулярна радиусу,
проведённому в точку касания.
проведённому в точку касания.

13. Теорема

Радиус сферы, проведённый в точку касания сферы и
плоскости, перпендикулярен к касательной плоскости.
Обратная теорема:
Если радиус сферы перпендикулярен к плоскости,
проходящей через его конец, лежащий на сфере, то эта
плоскость является касательной к сфере.

14. Вывод

Плоскость и сфера касаются в некоторой точке тогда и
только тогда, когда плоскость перпендикулярна радиусу,
проведённому в эту точку.

15.

Задачи
для самостоятельного
решения

16. Задача №1 Решите самостоятельно

1) Площадь большого круга шара равна 41. Найдите
площадь поверхности шара.
2) Площадь большого круга шара равна 10. Найдите
площадь поверхности шара
3) Площадь большого круга шара равна 26. Найдите
площадь поверхности шара

17. Задача №2 Решите самостоятельно

1) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 45 раз?
2) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 16 раз?
3) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 1,5 раза?

18. Задача №3 Решите самостоятельно

1) Даны два шара с радиусами 5 и 1. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
2) Даны два шара с радиусами 3 и 1. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
3) Даны два шара с радиусами 14 и 2. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?

19. Задача №4 Решите самостоятельно

1) Радиусы двух шаров равны 21, 72. Найдите радиус
шара, площадь поверхности которого равна сумме
площадей их поверхностей.
2) Радиусы двух шаров равны 8, 15. Найдите радиус шара,
площадь поверхности которого равна сумме площадей
их поверхностей.
3) Радиусы двух шаров равны 32, 60. Найдите радиус
шара, площадь поверхности которого равна сумме
площадей их поверхностей.