Similar presentations:
Вписані та центральні кути
1. 5 вересня Класна робота
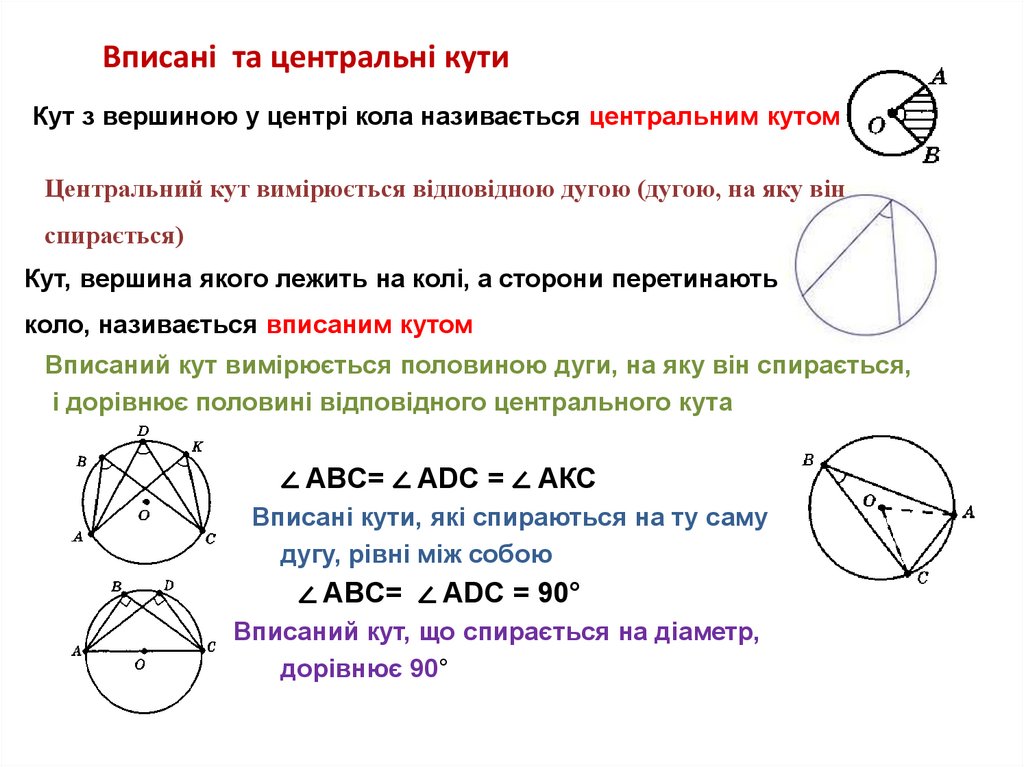
Вписані та центральні кутиКут з вершиною у центрі кола називається центральним кутом
Центральний кут вимірюється відповідною дугою (дугою, на яку він
спирається)
Кут, вершина якого лежить на колі, а сторони перетинають
коло, називається вписаним кутом
Вписаний кут вимірюється половиною дуги, на яку він спирається,
і дорівнює половині відповідного центрального кута
∠ ABC= ∠ ADC = ∠ АКС
Вписані кути, які спираються на ту саму
дугу, рівні між собою
∠ ABC= ∠ ADC = 90°
Вписаний кут, що спирається на діаметр,
дорівнює 90°
2.
3.
Метричні співвідношення в прямокутному трикутникуУ прямокутному трикутнику виконуються
такі співвідношення
b² = bc c
а² = аc c , де bc , аc - проекції катетів b і а на гіпотенузу
h² = аc bc
4.
5.
6.
7.
8.
Розв’язанняТак, тому що у кожного з них відповідні кути рівні
9.
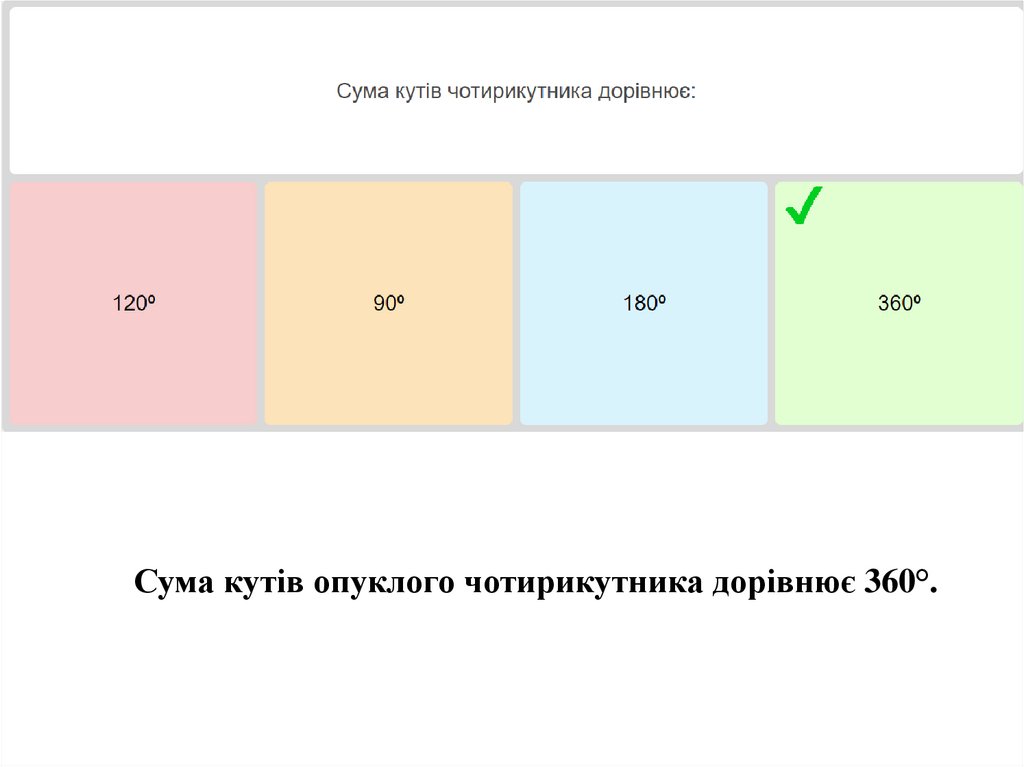
Сума кутів опуклого чотирикутника дорівнює 360°.10.
Теорема. Вписаний кут вимірюється половиною дуги, на яку вінопирається (дорівнює половині центрального кута, який опирається на
цю ж дугу)
11.
Середня лінія трапеції паралельна основам трапеції.Середня лінія трапеції дорівнює півсумі її основ.
(4+10):2 =7 (см)
12.
13.
14.
Розв’язанняЯкщо один з кутів прямокутного трикутника дорівнює 60, то інший дорівнює 90-60=30.
Напроти кута 30 градусів лежить катет, що дорівнює половині гіпотенузи
Х=6∙ 2=12
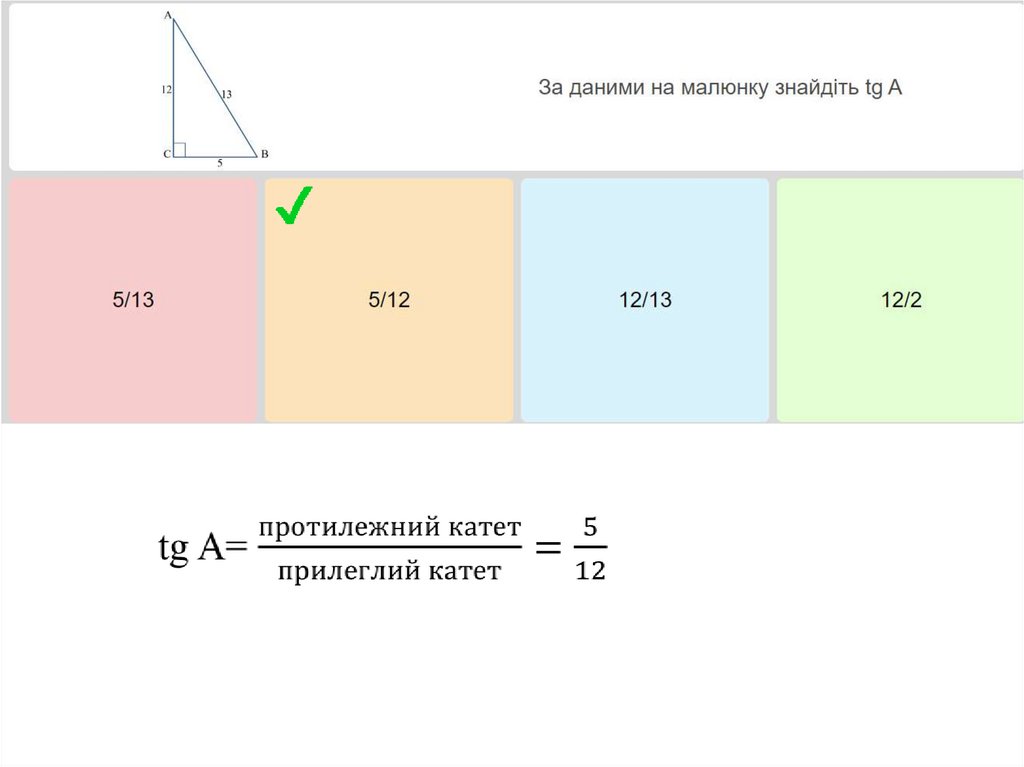
15.
16.
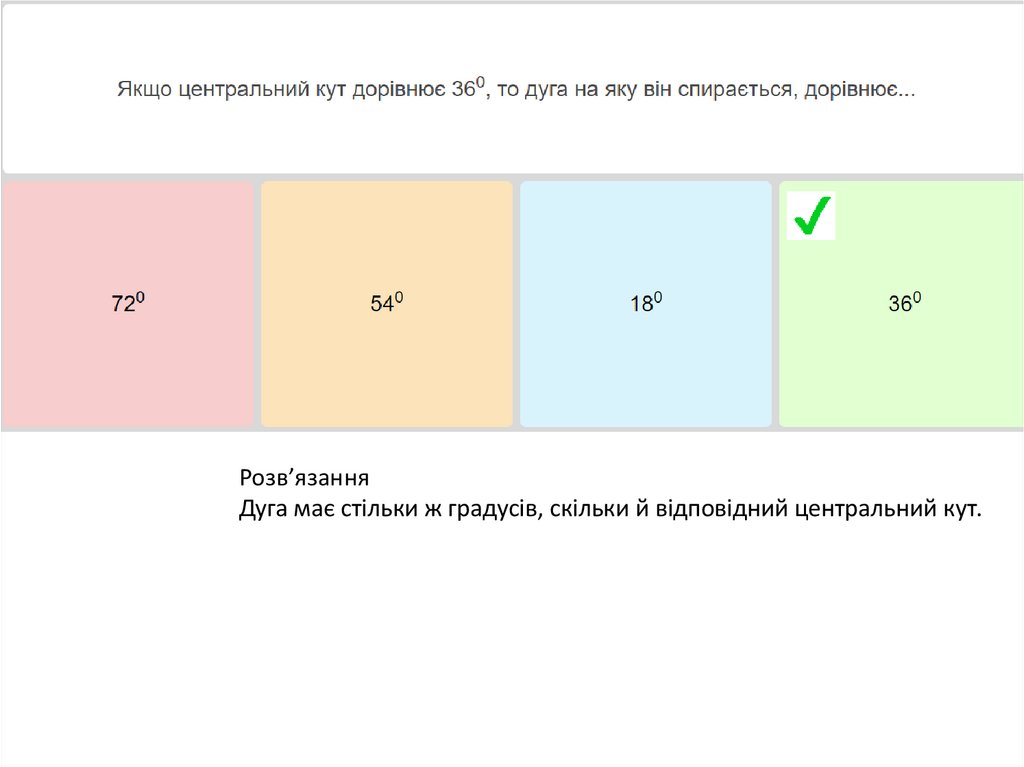
Розв’язанняДуга має стільки ж градусів, скільки й відповідний центральний кут.
17.
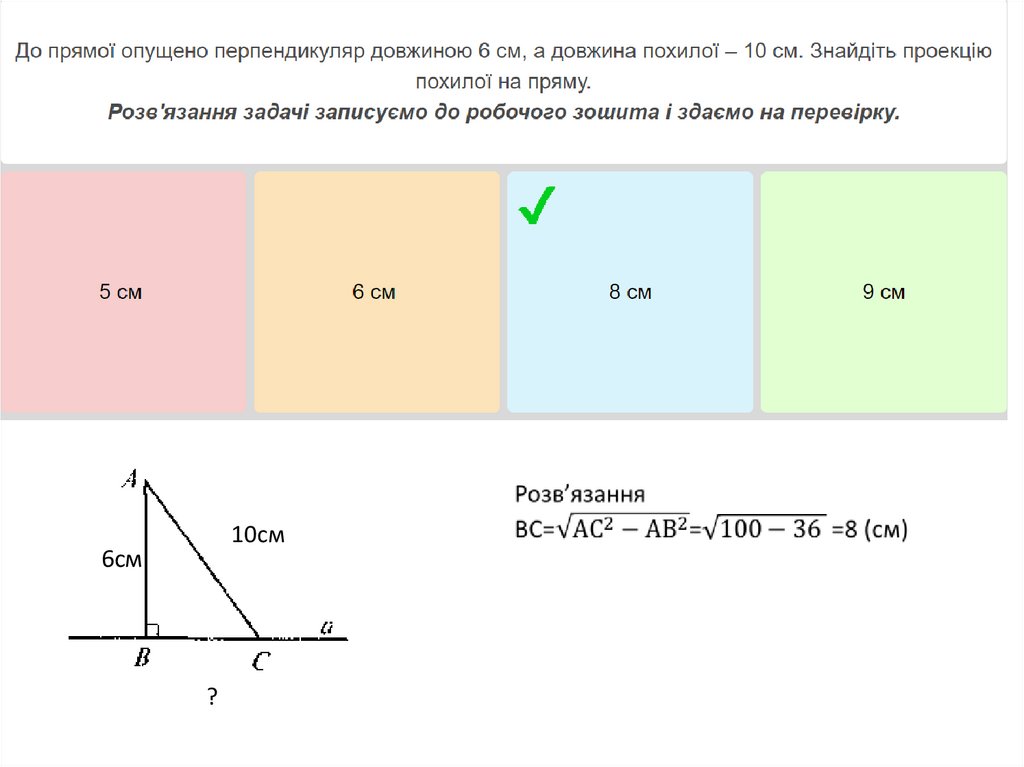
к18.
10см6см
?
19.
ВСЬОГОНАЙКРАЩОГО!












 mathematics
mathematics








