Рациональные числа

1.

Рациональные числа (1)
метапредмет – порядок

2.

ЗАДАЧИ УРОКА
Ч
И
С
Л
О
Соберите анаграмму и назовите ключевое
слово урока
Л
И
Ч
О
С
Важно! Уметь иллюстрировать с помощью
кругов Эйлера соотношение между
множествами натуральных, целых,
рациональных чисел;
использовать теоретико-множественную
символику для записи соотношений между
множествами;
сравнивать рациональные числа, выполнять
с ними арифметические действия;
представлять рациональные числа в виде
бесконечных десятичных периодических
дробей;
приводить примеры непериодических
десятичных дробей.
целеполагание

3.

МАТЕМАТИЧЕСКАЯ РАЗМИНКА
Вычислите:
вхождение в тему урока и создание условий для осознанного восприятия нового материала

4.

РАБОТАЕМ С КНИГОЙ
ЧИСЛОВЫЕ МНОЖЕСТВА
Числа 1, 2, 3, ..., которые используют при счёте,
?
называют натуральными
числами
N = { 1; 2; 3; 4; 5; …};
Натуральные числа, противоположные им числа
?
и число нуль составляют множество целых
чисел.
Z = {…; -2; -1; 0; 1, 2; 3; 4; … };
Целые и дробные числа составляют множество
?
рациональных
чисел.
Q = {…; - 3; − ; 0; 1; 1,76; 8; …};
4
7
Бесконечные десятичные непериодические
?
дроби образуют множество иррациональных
чисел
Множество рациональных чисел и множество
иррациональных чисел составляют множество
действительных
чисел.
?
организация и самоорганизация учащихся. организация обратной связи

5.

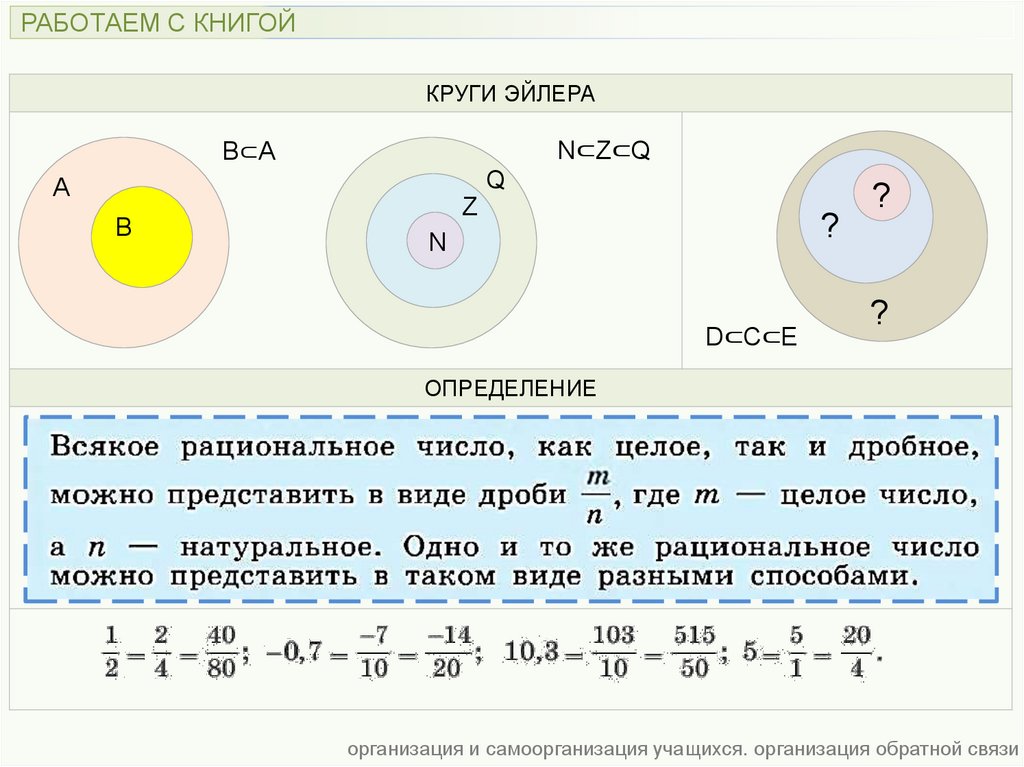
РАБОТАЕМ С КНИГОЙ
КРУГИ ЭЙЛЕРА
N⊂Z⊂Q
B⊂A
Q
A
B
Z
D
?
N
D⊂C⊂E
?
?
ОПРЕДЕЛЕНИЕ
организация и самоорганизация учащихся. организация обратной связи

6.

РАБОТАЕМ С КНИГОЙ
ПРЕОБРАЗОВАНИЯ
бесконечные
периодические
Любую конечную десятичную дробь и любое целое число можно записать в виде
бесконечной десятичной периодической дроби
организация и самоорганизация учащихся. организация обратной связи

7.

НАШИ ЗАДАЧИ
практикум

8.

НАШИ ЗАДАЧИ
практикум

9.

ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
проверка полученных результатов. коррекция

10.

ПОВТОРИМ
проверка полученных результатов. коррекция

11.

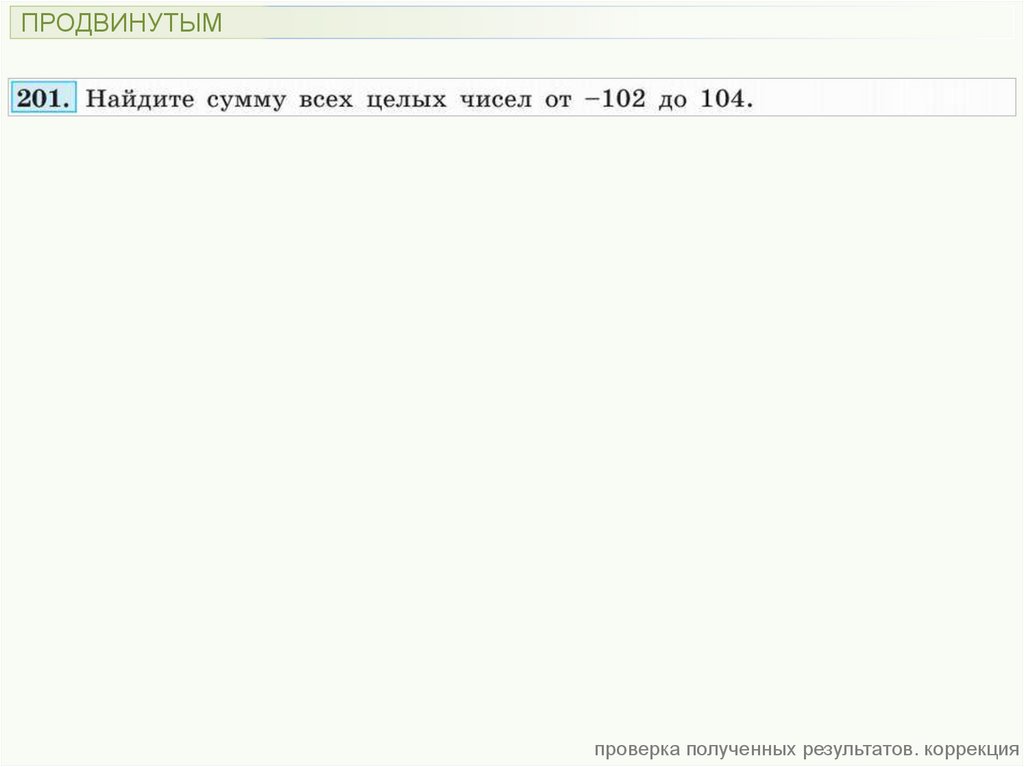
ПРОДВИНУТЫМ
проверка полученных результатов. коррекция

12.

ПРОВЕРЬ СЕБЯ
Какое из множеств (A или B) является подмножеством другого:
а) A — множество чётных чисел, B — множество чисел, кратных 6;
б) A — множество делителей числа 32, B — множество делителей
числа 16;
в) A — множество треугольников, B — множество равнобедренных
треугольников?
проверка полученных результатов. коррекция

13.

ПРОВЕРЬ СЕБЯ
проверка полученных результатов. коррекция

14.

ИТОГИ
Оцените активность своей
работы на уроке.
На уроке я:
а) активно работал(а);
б) работал(а), но не активно;
в) был(а) пассивен (пассивна).
Домашнее задание: § 1, п1, № 1(в), 2(в), 5(б, г, е, з, к) .
подведение итогов. рефлексия. домашнее задание