Основы геостатистики. Курс лекций

1.

Всегда в движении!
ОСНОВЫ ГЕОСТАТИСТИКИ
КУРС ЛЕКЦИЙ
Лялин Александр Викторович, доцент,
канд. геол.- минерал. наук,
Шадрин Арсений Олегович, ассистент
г. Когалым, 2024 г.

2.

ЛЕКЦИЯ № 1
СТАТИСТИКА В ГЕОЛОГИИ
Статистика и ее роль в исследованиях
Термин «статистика» употребляется в мировой литературе в различном смысле. Возможное и наиболее
общее определение статистики – обобщение и наглядное представление данных большого объема с
последующими выводами по этим данным. Ниже приведен ряд геологических примеров, иллюстрирующих
подобное понимание предмета: таблицы и графики, включающие широкий спектр данных нефтегазовой
геологии.
Применение статистических методов тесно связано с построением математических моделей. Они
позволяют распространить выводы, получаемые по ограниченному числу наблюдений (выборке), на
значительно большую группу объектов – популяцию (генеральную совокупность).
Применение подходящей статистической модели дает в руки исследователя аппарат, который усиливает
надежность обобщений путем распространения статистических выводов, полученных по выборке, на всю
совокупность.
Статистика – наука абстрактная, не решающая задачи исследования конкретных предметов или событий.
Статистика – наука методологическая, ее основные положения и технические приемы используются при
анализе вещественных данных того или иного вида. Геологические данные, подобно результатам
физических или химических исследований, характеризуют вещество. Роль статистики в геологии
заключается в разработке методов, позволяющих извлекать максимальную информацию из выборочных
данных, точно так же, как физики и химики изучают законы строения материи, используемые при
интерпретации геологических явлений.
2

3.

ЛЕКЦИЯ № 1
Главные типы статистических задач в геологии
Ниже приведены пять типов статистических задач, которые довольно часто возникают при
геологических исследованиях:
1. Оценка средних значений измеряемых признаков в совокупности.
2. Оценка характеристик изменчивости измеряемых признаков.
3. Выявление важных различий между признаками, измеряемыми в геологических совокупностях.
4. Оценка силы зависимости (статистическая корреляция) между измеряемыми признаками и
предсказание по одним признакам значений других.
5. Вычисление и подсчет систематических составляющих изменчивости признака по площади (тренд)
в задачах картирования характеристик совокупности.
6. Деление совокупности многомерных геологических объектов на классы. Дадим характеристику
каждому типу.
Первый из них – получение оценки неизвестного среднего значения измеряемого признака в классе
геологических объектов или событий.
Второй тип статистических задач в геологии – получение оценки характеристик изменчивости
измеряемых свойств геологических объектов или событий. Иногда исследуется только изменчивость
результатов измерения одного и того же признака единичного объекта (например, отметка глубины
залегания продуктивного горизонта в скважине). В этом случае целью может служить проверка
«воспроизводимости» некоторого метода измерения. Как пример статистической задачи иного
характера можно привести изучение изменчивости размеров пор в осадочной породе.
3

4.

ЛЕКЦИЯ № 1
Третий тип статистических задач в геологии включает сравнение групп геологических объектов
или событий. Сравнение методов измерения формы галек относится именно к этой категории
статистических исследований. В данном случае требуется ответить на вопрос: можно ли с
уверенностью утверждать, что средние значения результатов измерений одного и того же
геологического параметра двумя методами настолько близки, что эти методы можно
рассматривать как взаимозаменяемые? При положительном ответе целесообразно использовать
в дальнейших исследованиях менее трудоемкий метод.
Четвертый тип статистических задач в геологии связан с изучением зависимостей между
различными измеряемыми признаками (статистическая корреляция и т. п.). Эти задачи
возникают почти во всех геологических исследованиях, имеющих статистическое содержание.
Примером может служить изучение тесноты связи между различными показателями
нефтегазовой модели продуктивного горизонта (пористость, проницаемость, песчанистость и
т.д.).
Пятый тип статистических задач из приведенных выше – это тренд-анализ – изучение
изменчивости признаков по площади. Эти задачи охватывают проблемы анализа и
интерпретации картографического материала, особенно карт контурного типа. Систематические
изменения того или иного вида – физические или химические, большие или незначительные –
всегда отмечаются на структурных и фациальных картах, на картах минералогического состава
гранитов и многих других. В соответствии с такими изменениями по площади обычно выбирают
различные масштабы карт, что позволяет выделить на мелкомасштабных картах главные
направления изменений, на которые наложены менее значительные изменения, представляющие
собой несистематические флуктуации.
4

5.

ЛЕКЦИЯ № 1
Отделение тренда от наложенных на него изменений меньшего порядка позволяет, с одной
стороны, изучать явления в мелком масштабе, а с другой – исследовать малые изменения,
наблюдаемые в крупном масштабе, т. е. аномалии, имеющие большое значение при поисках
рудных тел или месторождений углеводородного сырья. Этот тип задач относится к анализу
линейных моделей, который иногда называют регрессионным анализом.
Шестая задача – довольно сложная задача, которая во многих геологических задачах обычно
решалась на уровне качественного моделирования. Естественно, что при этом разбиение на
классы осуществлялось условно, по одному двум параметрам. Качественное разбиение на
классы позволяло внести в этот процесс много субъективного, связанного с точкой зрения
отдельных исследователей и научных школ. Однако с развитием вычислительной техники
трудоемкие расчеты стало возможным проводить в течение очень короткого времени, используя
при этом математический аппарат дискриминантного анализа. Это задачи искусственного
интеллекта ЭВМ.
Математические модели
Как было сказано выше, математическая модель – это абстрактный аналог физической модели, в
которой объекты, силы, события и т. п. заменены математическими понятиями – переменными,
параметрами и константами. Математические модели можно сгруппировать в несколько типов –
детерминированные и статистические модели, а также в модели стохастических процессов. Чтобы
впоследствии лучше различать статистические и детерминированные модели, последние будут
рассмотрены достаточно детально.
5

6.

ЛЕКЦИЯ № 1
Детерминированные модели
Рассмотрим математическое содержание детерминированных модели на
следующем примере.
Закон Стокса, широко используемый при анализе размеров частиц в
тонкозернистых осадках, выражает связь между скоростью осаждения и
радиусом частицы, имеющей форму шара, в вязкой жидкости. Если на частицу в
жидкости ничего не действует, кроме силы тяжести, она начинает опускаться,
причем это опускание сопровождается некоторым ускорением, что происходит
до тех пор, пока сопротивление жидкости, вызванное вязкостью, не оказывается
равным силе тяжести. После достижения этого равенства частица опускается с
постоянной скоростью, называемой предельной скоростью осаждения.
Закон Стокса был выведен в 1851 году на основе принципов гидродинамики.
Стокс показал, что сопротивление, которое оказывает жидкость на медленно
опускающуюся в ней частицу, пропорционально ее радиусу r, динамической
вязкости жидкости и скорости движения частицы V:
Fs =6 r V.
(1.1)
6

7.

ЛЕКЦИЯ № 1
Выражение (1.1) характеризует силу, препятствующую движению частицы. Она
уравновешена силой тяжести, под действием которой частица движется вниз.
Частица, свободно падающая в вакууме, подвергается действию только силы Fg,
равной произведению объема частицы (4/3) r 3, ее плотности 1 и ускорению
силы тяжести g:
Fg = (4/3) r 3 1g
(1.2)
Если частица находится в жидкости, то, согласно закону Архимеда, на нее будет
действовать сила, направленная вверх. Эта сила Fb равна произведению объема
частицы, плотности жидкости р2 и ускорению силы тяжести (g):
Fb = (4/3) r 3 2g
(1.3)
Это выражение отличается от предыдущего только величиной 2, которой заменен
символ 1. Вычитая выражение (2.3) из выражения (2.2), определим силу, которая
действует на частицу, свободно падающую в жидкости:
Fd = (4/3) r 3( 1 - 2)g
(1.4)
Эта сила равна произведению объема частицы, разности между ее удельным весом
и удельным весом жидкости, умноженному на ускорение силы тяжести. Закон
Стокса для постоянной предельной скорости осаждения сферической частицы
теперь можно выразить, приравняв выражения (2.1) и (2.4) и решив полученное
уравнение относительно V:
2( 1 2 )gr 2
V
.
(1.5)
9
7

8.

ЛЕКЦИЯ № 1
Из этого следует, что закон Стокса выражает функциональную связь между зависимой переменной
V и аргументом r, так что если значение r задано для сферической частицы с данной плотностью,
находящейся в жидкости с определенным удельным весом и вязкостью, то значению r
соответствует одно и только одно значение V. Именная такая модель называется
детерминированной.
Закон Стокса иллюстрирует и другое важное свойство многих математических моделей,
заключающееся в том, что «движущие силы» контролируют любое конкретное значение зависимой
переменной. Так, из уравнения (2.5) следует, что предельная скорость осаждения сферической
частицы в вязкой жидкости прямо пропорциональна разности соответствующих плотностей,
ускорению силы тяжести, квадрату радиуса частицы и обратно пропорциональна динамической
вязкости жидкости.
Соответствие детерминированной модели реальному явлению можно проверить экспериментально.
Такая проверка неоднократно проводилась для закона Стокса. В результате было установлено, что
очень хорошая согласованность теории и эмпирических данных наблюдается при осаждении в воде
частиц с плотностью около 2,8 и диаметром от 0,0005 до 0,08 мм. На более мелкие частицы в
значительной степени начинает влиять брауновский эффект, более же крупные частицы
подвержены воздействию турбулентных завихрений.
Все это указывает на то, что детерминированные модели хорошо согласуются с реальными
явлениями только в некоторой ограниченной области. Если же эту область расширить,
согласованность ухудшается. В том случае, когда модель используется для некоторой
ограниченной области условий, погрешности уравнения становятся практически
незначительными. Однако эти ошибки сильно возрастают по мере того, как модель
распространяется на области, выходящие за пределы теоретических ограничений и
предположений.
8

9.

ЛЕКЦИЯ № 1
Модели стохастических процессов
Термин «стохастическая модель» вообще является синонимом термина, «статистическая
модель». Как было показано выше, удобная статистическая модель содержит одну (или более)
случайную компоненту, связанную с погрешностями измерений, ошибкой уравнения или же с
собственной изменчивостью измеряемых объектов, как, например, различия форм
совокупности антиклинальных структур. Модель стохастического процесса может содержать
аналогичные случайные компоненты, но описывает их изменения в зависимости от
некоторого неслучайного параметра, в качестве которого обычно выбирается время. Такие
модели, построенные на вероятностной основе, описывают явления лучше, чем
детерминированные модели. Известные примеры стохастических моделей – модель процесса
случайного блуждания при изучении продольных профилей речных долин (Л. Лиополд, В.
Лангбейн, 1962), модель движения жидкости по капиллярам (А. Шейдеггер, 1958) и др.
Модели стохастических процессов и детерминированные построения являются
аналитическими в том смысле, что они требуют четкого определения тех «сил», которые
позволяют наблюдать структуру процесса. Оба эти типа моделей различаются лишь тем, что в
детерминированной отсутствуют случайные компоненты, так что процесс точно определен в
любой заданный момент времени.
9

10.

ЛЕКЦИЯ № 1
Качественные (понятийные) модели
Как известно, понятийная модель является мысленным образом некоторого природного явления.
Такие модели бывают схематическими или же выраженными как качественно, так и количественно;
они основаны на наблюдениях и служат для выражения некоторых явлений реального мира в
идеализированной форме. Понятийную модель обычно упрощают с целью сохранить главные
особенности изучаемого явления и избавиться от несущественных деталей. Такую модель в
дальнейшем можно формализовать и представить в виде масштабной, детерминированной или
статистической.
Понятийные модели в схематической форме чаще всего бывают качественными, но они в
значительной степени помогают при разработке выборочного плана; кроме того, ими пользуются
как рабочими моделями и для проверки их соответствия реальным явлениям или для предсказания.
В общем случае построение качественной модели включает выявление: исходных компонент,
главных (определяющих факторов) и результатов изучаемого процесса.
Различные понятийные модели, представленные в виде диаграмм типа процесс – результат, а также
других типов, можно разделить на следующие группы:
1) стратиграфические модели и модели фаций;
2) модели, связанные с изучением изверженных и осадочных пород, охватывающие задачи
петрогенеза и вопросы исследования процессов;
3) геоморфологические модели, связанные с изучением свойств земной поверхности или речных
бассейнов;
4) палеонтологические модели.
Этот далеко не полный перечень показывает, насколько широко применяются модели в различных
отраслях геологии и как непрерывно возрастает интерес к данному вопросу.
10

11.

ЛЕКЦИЯ № 2
Основные задачи анализа пространственных данных
Проблемы пространственного моделирования
Существует огромное количество пространственно распределенной информации,
собранной в базы и банки данных по окружающей среде. Задача ее интерпретации,
анализа и дальнейшего использования представляется чрезвычайно важной и требует
комплексного системного подхода. Статистическое моделирование пространственных
явлений позволяет обобщить имеющиеся измерения и получить модель их
распределения в пространстве.
Пространственное моделирование применяется во многих сферах человеческой
деятельности. Так, при климатическом моделировании анализируются измерения
температуры, осадков, скорости ветра и т. д. в различных точках пространства. При
моделировании загрязнения окружающей среды используются измерения (пробы
грунта, воды, воздуха, дистанционное зондирование) в различных местах. В задачах
геологии моделируются свойства пород в промежутке между скважинами, где
делаются измерения. В медицинской географии анализируются факторы, влияющие
на уровень
заболеваний,
и
моделируется
распространение эпидемий.
Пространственно распределенные данные используются при моделировании запасов
полезных ископаемых и рыбных ресурсов, криминогенной ситуации и природных
катастроф (оползней, лавин и пр.).
11

12.

ЛЕКЦИЯ № 2
Глубокий анализ и моделирование пространственных данных требуют применения комплексного
подхода и различных методов, характеризующих ту или иную особенность явления. Сложность
такого анализа обусловлена несколькими факторами: наличием больших объемов количественной
и качественной информации по исследуемому явлению, многомасштабностью и
многопеременностью, наличием различных факторов влияния. Мы изучим в наших лекциях
элементы методологии геостатистического анализа пространственно распределенных данных и
приведем примеры исследования с применением этих методов для реальных данных, связанных
степенью распределения геолого-геофизических атрибутов, структурными условиями территорий
изучения, геомоделированием свойств пород, гидрогеологией, моделированием ресурсов
углеводородного сырья.
Постановка геостатистической задачи
При работе с пространственными данными обычно имеется некоторое количество измерений
изучаемой переменной в различных точках, число которых ограниченно. Итак, есть область, на
которой проведен ряд измерений некоторой величины Z. Эти измерения проведены в произвольно
распределенном по области наборе точек (x, y), которые мы будем называть сетью мониторинга
(рис. 1.1). Но есть и участки области, не покрытые измерениями, о значениях величины Z в
которых хотелось бы получить информацию. Наиболее часто требуется оценить значение
наблюдаемой величины в непромеренной точке X на основе имеющихся данных, т. е. решить
задачу интерполяции. Данные измерений, как правило, дискретны и пространственно неоднородно
распределены. Анализ данных и его результаты зависят от качества и количества исходных
данных, от методов и моделей обработки данных.
12

13.

ЛЕКЦИЯ № 2
13

14.

ЛЕКЦИЯ № 2
Приведем здесь ряд конкретных задач, для решения которых необходимо
применение комплекса исследований с помощью методов геостатистики —
статистики пространственно распределенной (региональной) информации:
• оценить значение в точке, где измерение не проводилось;
• нарисовать карту, построить изолинии (определить значения на плотной сетке);
• оценить ошибку интерполяционной оценки;
• оценить значение переменной, по которой мало измерений, используя значения
другой коррелированной с ней переменной, по которой проведено много
измерений;
• определить вероятность того, что значения наблюдаемой переменной превысят
заданный уровень в интересующей нас области;
• получить набор равновероятных стохастических пространственных реализаций
распределения наблюдаемой переменной.
Первые три задачи — примеры задач регрессии или классификации (в
зависимости от типа исходных значений). Две последние задачи относятся к
вероятностному анализу и связаны с оценками риска. Отдельные главы данной
книги будут посвящены решению этих задач.
14

15.

ЛЕКЦИЯ № 2
Подходы к анализу пространственно распределенных данных
Существует несколько подходов к анализу и обработке пространственно распределенных данных,
которые можно условно разделить на три группы:
• детерминистические модели (интерполяторы) — линейная интерполяция на основе триангуляции,
метод обратных расстояний в степени, мульти-квадратичные уравнения и т. п.;
• геостатистика — модели, базирующиеся на статистической интерпретации данных;
• алгоритмы, основанные на обучении — искусственные нейронные сети, генетические алгоритмы,
статистическая теория обучения машин векторов поддержки (Support Vector Machines).
Геостатистический анализ позволяет значительно повысить уровень надежности и качество
решений, принимаемых на основе использования пространственно распределенной информации.
Современные тенденции геостатистики связаны с развитием методов стохастического
моделирования (пространственных аналогов методов Монте-Карло), методов, основанных на
многоточечной статистике, гибридных моделей с использованием алгоритмов искусственного
интеллекта, с использованием дополнительной информации различного вида и приложениями в
области обработки и передачи изображений, с расширением на временной и пространственновременной анализы и многими направлениями.
Одним из важных составляющих традиционной геостатистики является пространственный
корреляционный анализ, или вариография. Несмотря на кажущуюся простоту исходных формул,
вариография позволяет сделать глубокие выводы о статистической природе данных и структуре
адекватных моделей. В принципе экспериментальная вариография, основанная на исходных
данных, может быть использована в большинстве задач пространственного оценивания независимо
от метода интерполяции наравне с традиционным статистическим анализом.
15

16.

ЛЕКЦИЯ № 2
Основные этапы анализа и моделирования пространственных данных
Первым и весьма важным этапом исследования является современный статистический анализ
данных, позволяющий определить наличие ошибок и выбросов (outliers) в данных, оценить
базовые статистические закономерности, провести корреляционный анализ при наличии
нескольких переменных и т. п. Если данные собраны на нерегулярной кластерной сети
мониторинга, может потребоваться пространственная декластеризация для получения
репрезентативной глобальной статистики — средних, вариаций, гистограмм. Если сеть
мониторинга имеет зоны с заметно более высокой плотностью измерений, чем остальная область,
то сеть мониторинга кластерная. Если при этом зоны повышенной плотности измерений
характеризуются более высокими (или, наоборот, низкими) значениями измерений, возникает
необходимость в декластеризации. Иначе оценки всех статистических характеристик будут
искажены, например оценка среднего будет завышена (или, наоборот, занижена). Процедура
декластеризации ориентирована на устранение такого рода искажений.
Можно рассматривать два основных типа декластеризации — выборочную и весовую.
Выборочная декластеризация связана с выбором части данных из кластеров, весовая
предполагает задание весов, с которыми используются измерения.
Оценить некоторые пространственные особенности данных позволяет статистика с движущимся
окном: область разбивается на подобласти, в каждой из которых проводится независимый
статистический анализ. Дальнейший пространственный анализ предполагает исследование и
моделирование пространственной корреляции между данными по одной или нескольким
переменным. Мерой пространственной корреляции является вариограмма — статистический
момент второго порядка.
16

17.

ЛЕКЦИЯ № 2
Для получения наилучшей в статистическом смысле пространственной оценки
используются модели из семейства кригинга (kriging) — наилучшего линейного
несмещенного оценивателя (best linear unbiased estimator — BLUE).
Кригинг является «наилучшим» оценивателем в статистическом смысле в классе
линейных интерполяторов — его оценка обладает минимальной вариацией ошибки.
Важное свойство кригинга — точное воспроизведение значений измерений в
имеющихся точках (точный оцениватель). В отличие от многочисленных
детерминистических методов, оценка кригинга сопровождается оценкой ошибки
интерполяции в каждой точке. Полученная ошибка позволяет охарактеризовать
неопределенность полученной оценки данных при помощи доверительных
интервалов или «толстых» изолиний. При применении любой модели
интерполяции встает вопрос о подборе оптимальных модельно-зависимых
параметров. Легко показать, что даже в случае использования одного и того же
метода интерполяции можно получить качественно разные результаты в
зависимости от выбора модельных параметров. Выбор оптимальных параметров
опирается на пошаговое исследование характера и структуры данных.
Эффективными инструментами подбора модельных параметров являются методы
кросс-валидации (cross-validation), складного ножа (jack-knife), бутстреп (bootstrap).
17

18.

ЛЕКЦИЯ № 2
Все они основаны на проведении оценки для части точек измерений, выбранных из
основного набора по остальным данным с последующим вычислением ошибки
оценки. После оценок по всем точкам, наборам или выборкам оценивается
среднеквадратичная ошибка полученных оценок. По ней сравниваются различные
методы или выбираются наилучшие параметры метода. В геостатистике
традиционно более широко используется кросс-валидация. При проведении
анализа реальных данных эксперты часто сталкиваются с проблемой малого
количества измерений по интересующей переменной, например вследствие их
дороговизны или небезопасности взятия проб. При этом в наличии может
оказаться большое (избыточное) количество «дешевых» измерений переменной,
которая достаточно сильно коррелированна с основной. Встает вопрос, как можно
использовать «дешевую» информацию для улучшения оценки переменной,
информация по которой «дорога». В рамках многопеременной геостатистики
существует модель совместной пространственной интерполяции нескольких
коррелированных переменных — кокригинг. Кокригинг позволяет значительно
улучшить качество оценки, перейти из области экстраполяции в область
интерполяции, уменьшить ошибку оценки за счет использования дополнительной
«дешевой» информации по коррелированным переменным.
18

19.

ЛЕКЦИЯ № 2
Часто результатом пространственного анализа данных в рамках квалифицированной
поддержки принятия решений являются вероятностные карты. Вероятностное картирование
дает возможность оценить уровень риска по превышению или непревышению заданного
уровня значения пространственной переменной. Оно также используется при оптимизации
решений, когда пространственный анализ данных является только промежуточным этапом. В
рамках геостатистики для вероятностного картирования используются нелинейные модели
кригинга, в частности индикаторный кригинг. Он позволяет рассчитать локальную функцию
распределения в точке оценивания. В качестве результатов составляются карты вероятности,
карты средних оценок, карты оценок с заданной вероятностью превышения, которые
используются в процессе принятия решений. Применение различных детерминистических
или геостатистических моделей интерполяции/оценивания всегда дает единственное и
сглаженное, не воспроизводящее изначальную вариабельность данных значение оценки в
интересующей точке при выбранных модельных параметрах. Стохастическое моделирование
является альтернативным подходом, дающим возможность воспроизвести исходную
вариабельность и получить сколь угодно много равновероятных реализаций
пространственной функции в области. Равновероятные реализации позволяют описать
пространственную вариабельность (изменчивость) и неопределенность пространственной
функции, оценить вероятности и риск. При использовании стохастического моделирования
удается избежать «сглаженной» картины оценки, которая присуща большинству моделей
интерполяции. Это позволяет получать корректные результаты в таких задачах, как,
например, расчет объема нефтяного резервуара, «длины» береговой линии и т. п.
19

20.

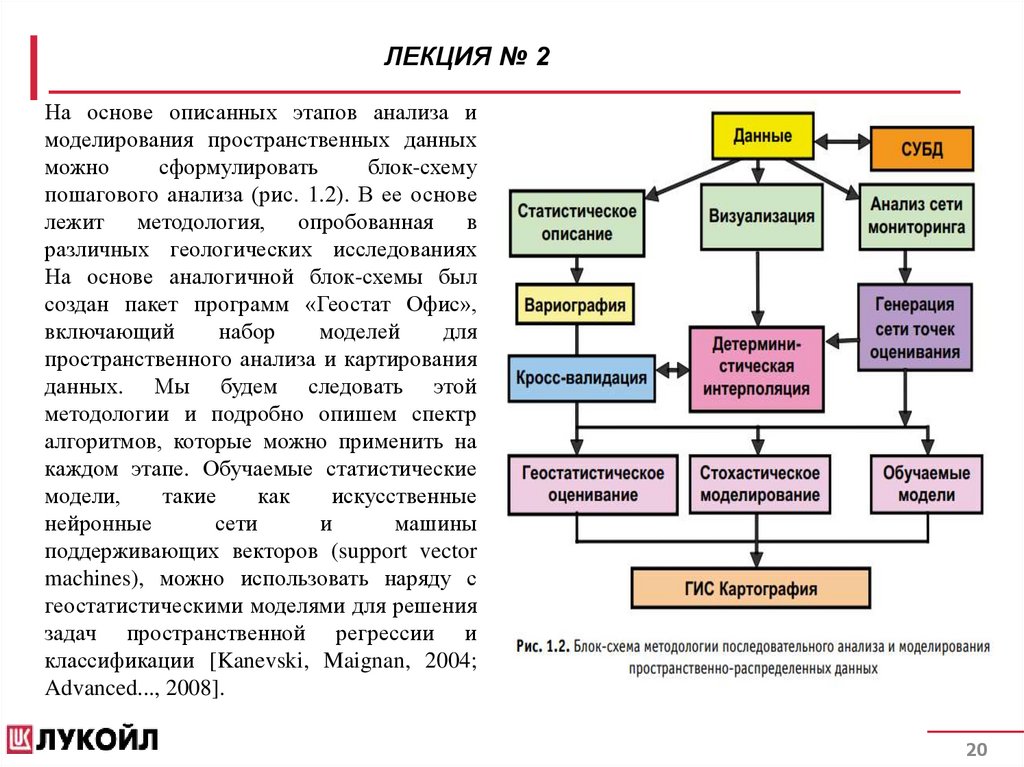
ЛЕКЦИЯ № 2
На основе описанных этапов анализа и
моделирования пространственных данных
можно
сформулировать
блок-схему
пошагового анализа (рис. 1.2). В ее основе
лежит методология, опробованная в
различных геологических исследованиях
На основе аналогичной блок-схемы был
создан пакет программ «Геостат Офис»,
включающий
набор
моделей
для
пространственного анализа и картирования
данных. Мы будем следовать этой
методологии и подробно опишем спектр
алгоритмов, которые можно применить на
каждом этапе. Обучаемые статистические
модели,
такие
как
искусственные
нейронные
сети
и
машины
поддерживающих векторов (support vector
machines), можно использовать наряду с
геостатистическими моделями для решения
задач пространственной регрессии и
классификации [Kanevski, Maignan, 2004;
Advanced..., 2008].
20

21.

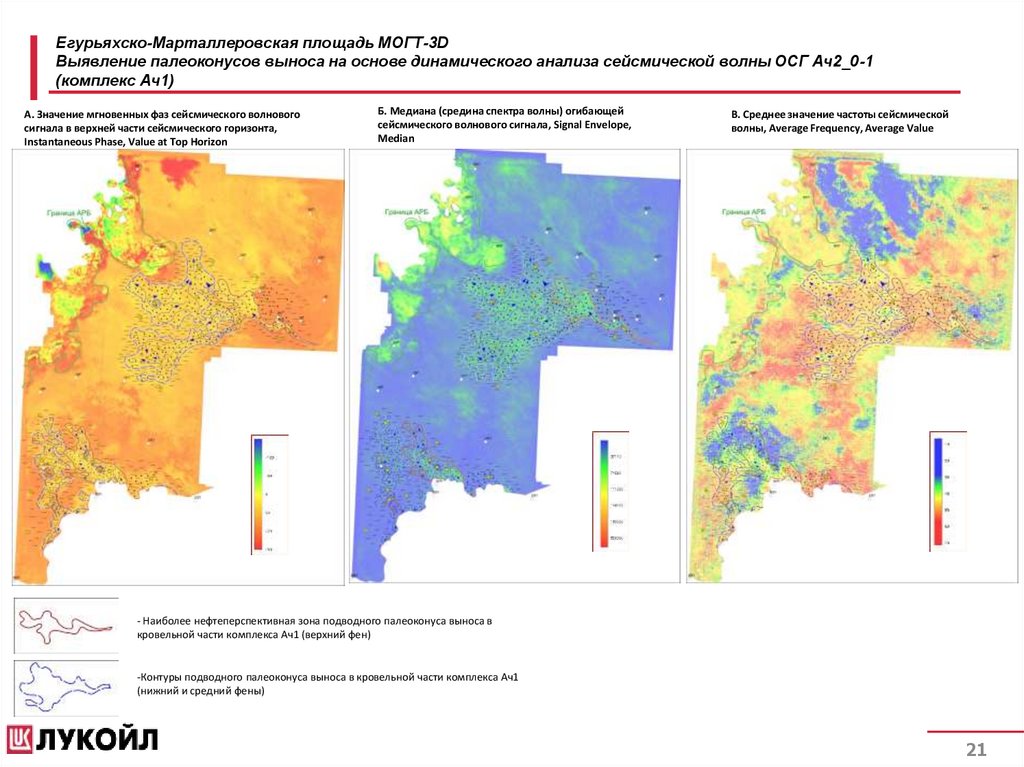
Егурьяхско-Марталлеровская площадь МОГТ-3D
Выявление палеоконусов выноса на основе динамического анализа сейсмической волны ОСГ Ач2_0-1
(комплекс Ач1)
А. Значение мгновенных фаз сейсмического волнового
сигнала в верхней части сейсмического горизонта,
Instantaneous Phase, Value at Top Horizon
Б. Медиана (средина спектра волны) огибающей
сейсмического волнового сигнала, Signal Envelope,
Median
В. Среднее значение частоты сейсмической
волны, Average Frequency, Average Value
- Наиболее нефтеперспективная зона подводного палеоконуса выноса в
кровельной части комплекса Ач1 (верхний фен)
-Контуры подводного палеоконуса выноса в кровельной части комплекса Ач1
(нижний и средний фены)
21

22.

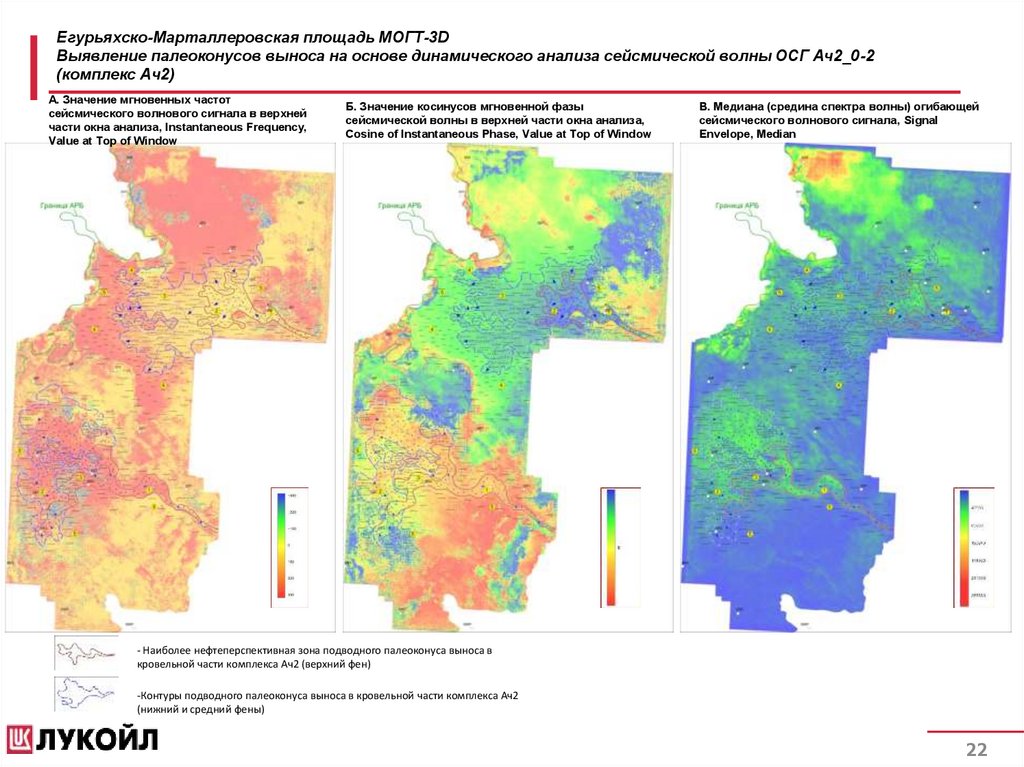
Егурьяхско-Марталлеровская площадь МОГТ-3D
Выявление палеоконусов выноса на основе динамического анализа сейсмической волны ОСГ Ач2_0-2
(комплекс Ач2)
А. Значение мгновенных частот
сейсмического волнового сигнала в верхней
части окна анализа, Instantaneous Frequency,
Value at Top of Window
Б. Значение косинусов мгновенной фазы
сейсмической волны в верхней части окна анализа,
Cosine of Instantaneous Phase, Value at Top of Window
В. Медиана (средина спектра волны) огибающей
сейсмического волнового сигнала, Signal
Envelope, Median
- Наиболее нефтеперспективная зона подводного палеоконуса выноса в
кровельной части комплекса Ач2 (верхний фен)
-Контуры подводного палеоконуса выноса в кровельной части комплекса Ач2
(нижний и средний фены)
22

23.

Северо-Егурьяхский-2 ЛУ. Применение сектральной декомозиции.
Выкопировка из презентации: Анализ выполнения поручения пункта 5.4.15 протокола
МИ-47п от 23.03.2018 г. (К.Н.Кунин, Е.А.Фомина, БГРР 23.01.2019 ).
23

24.

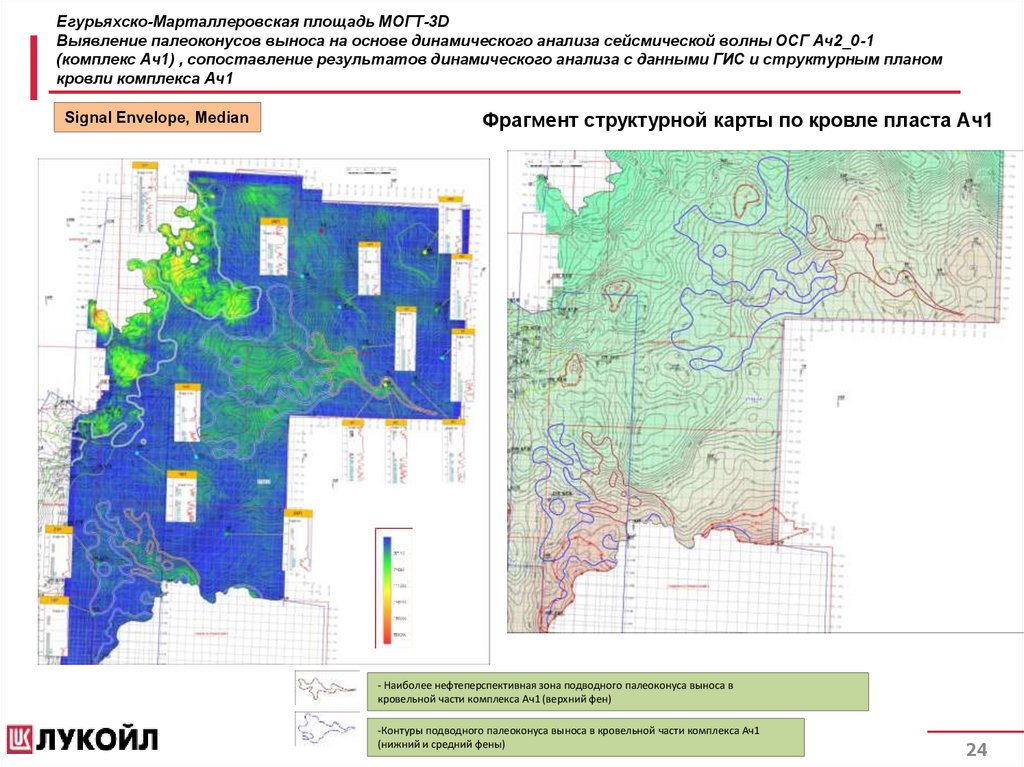
Егурьяхско-Марталлеровская площадь МОГТ-3D
Выявление палеоконусов выноса на основе динамического анализа сейсмической волны ОСГ Ач2_0-1
(комплекс Ач1) , сопоставление результатов динамического анализа с данными ГИС и структурным планом
кровли комплекса Ач1
Signal Envelope, Median
Фрагмент структурной карты по кровле пласта Ач1
- Наиболее нефтеперспективная зона подводного палеоконуса выноса в
кровельной части комплекса Ач1 (верхний фен)
-Контуры подводного палеоконуса выноса в кровельной части комплекса Ач1
(нижний и средний фены)
24

25.

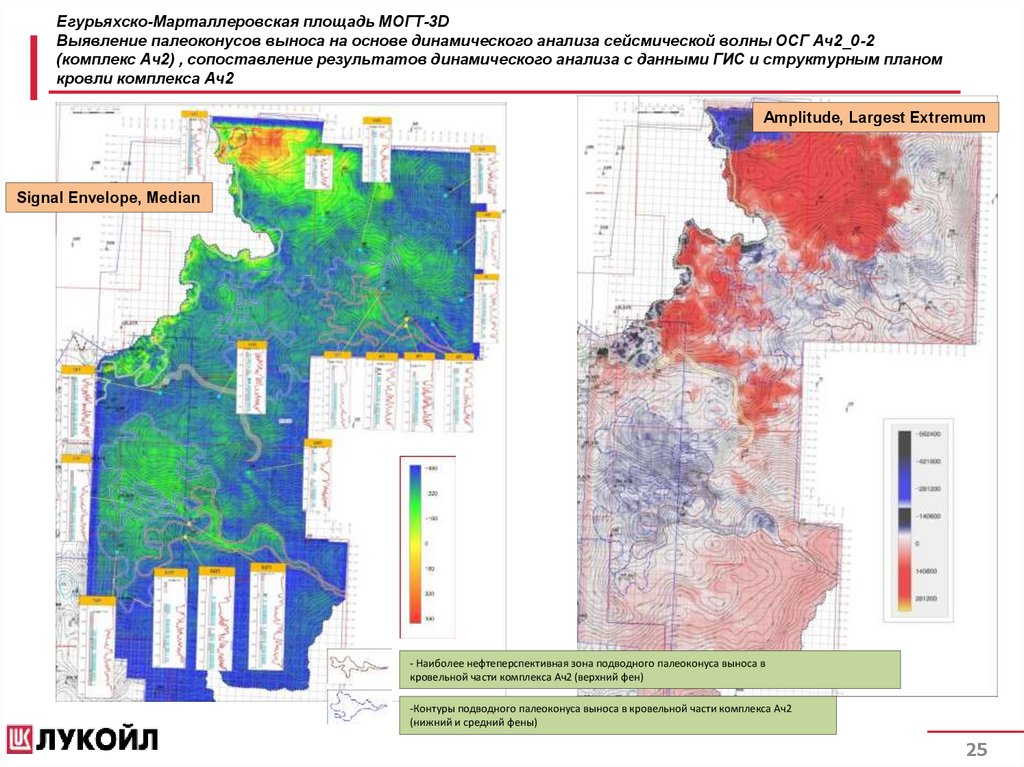
Егурьяхско-Марталлеровская площадь МОГТ-3D
Выявление палеоконусов выноса на основе динамического анализа сейсмической волны ОСГ Ач2_0-2
(комплекс Ач2) , сопоставление результатов динамического анализа с данными ГИС и структурным планом
кровли комплекса Ач2
Amplitude, Largest Extremum
Signal Envelope, Median
- Наиболее нефтеперспективная зона подводного палеоконуса выноса в
кровельной части комплекса Ач2 (верхний фен)
-Контуры подводного палеоконуса выноса в кровельной части комплекса Ач2
(нижний и средний фены)
25

26.

Егурьяхско-Марталлеровская площадь МОГТ-3D
Временные разрезы по линии профилей Xline240, 280
26

27.

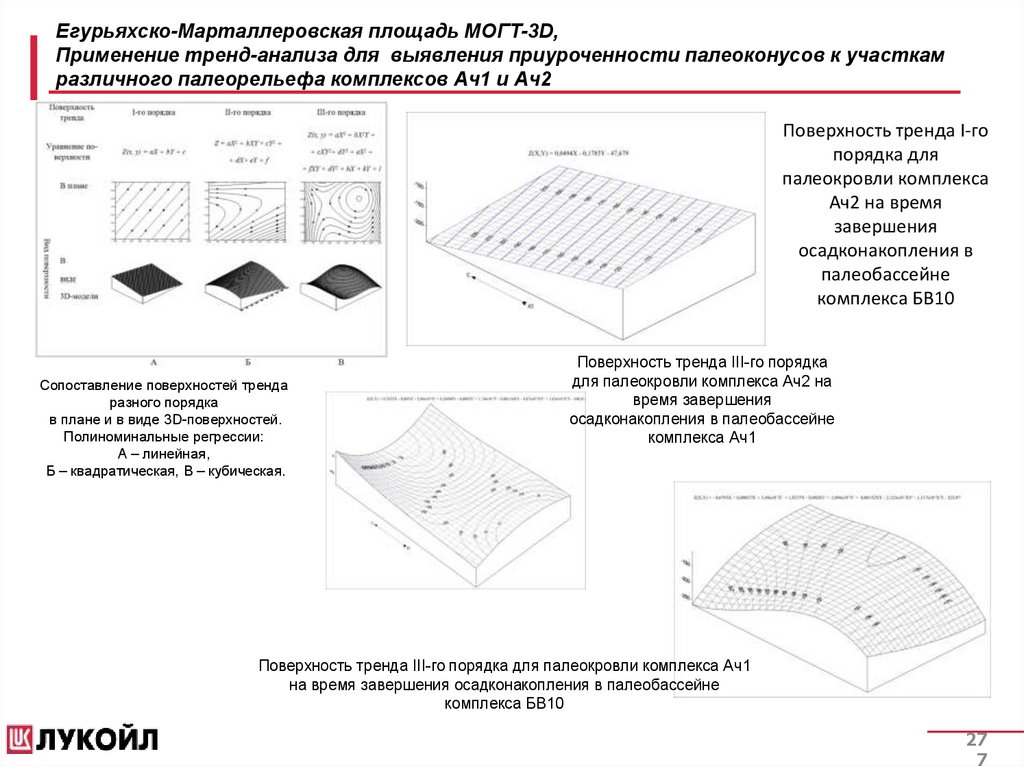
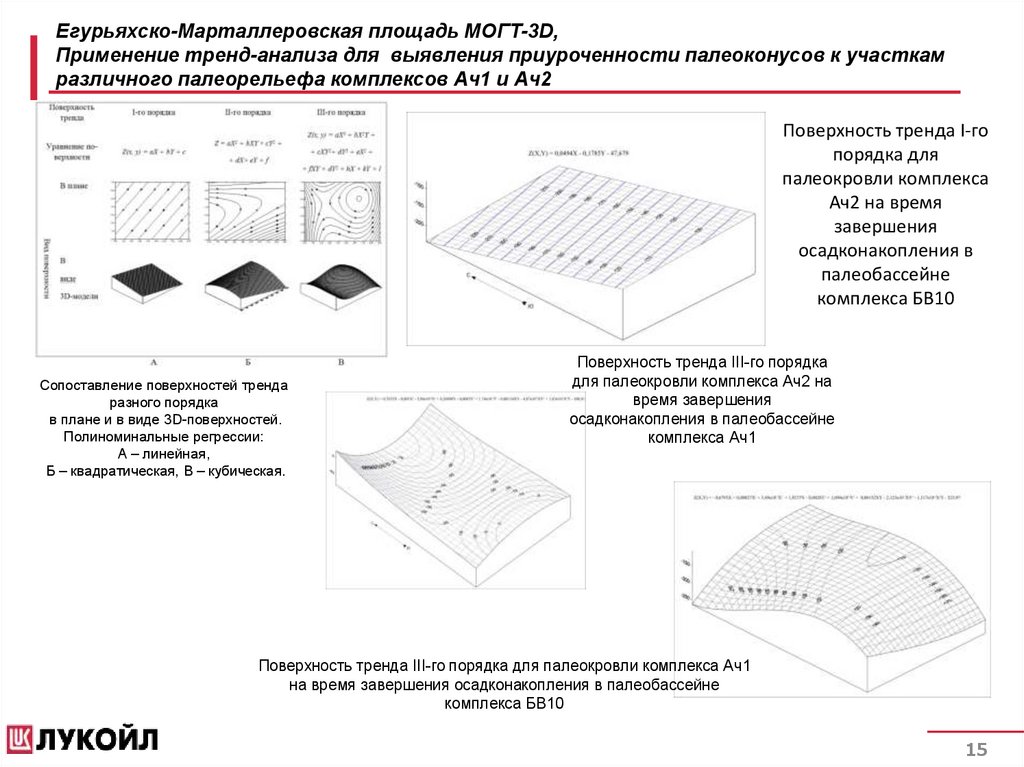
Егурьяхско-Марталлеровская площадь МОГТ-3D,
Применение тренд-анализа для выявления приуроченности палеоконусов к участкам
различного палеорельефа комплексов Ач1 и Ач2
Поверхность тренда I-го
порядка для
палеокровли комплекса
Ач2 на время
завершения
осадконакопления в
палеобассейне
комплекса БВ10
Сопоставление поверхностей тренда
разного порядка
в плане и в виде 3D-поверхностей.
Полиноминальные регрессии:
А – линейная,
Б – квадратическая, В – кубическая.
Поверхность тренда III-го порядка
для палеокровли комплекса Ач2 на
время завершения
осадконакопления в палеобассейне
комплекса Ач1
Поверхность тренда III-го порядка для палеокровли комплекса Ач1
на время завершения осадконакопления в палеобассейне
комплекса БВ10
27
7

28.

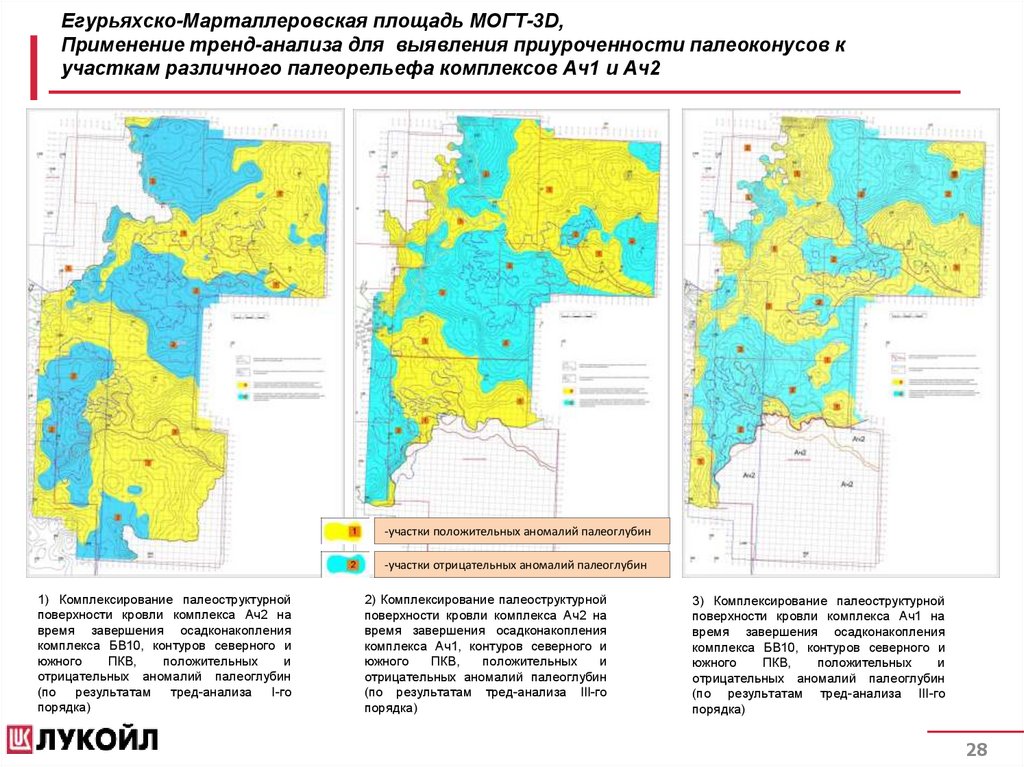
Егурьяхско-Марталлеровская площадь МОГТ-3D,
Применение тренд-анализа для выявления приуроченности палеоконусов к
участкам различного палеорельефа комплексов Ач1 и Ач2
-участки положительных аномалий палеоглубин
-участки отрицательных аномалий палеоглубин
1) Комплексирование палеоструктурной
поверхности кровли комплекса Ач2 на
время завершения осадконакопления
комплекса БВ10, контуров северного и
южного
ПКВ,
положительных
и
отрицательных аномалий палеоглубин
(по
результатам
тред-анализа
I-го
порядка)
2) Комплексирование палеоструктурной
поверхности кровли комплекса Ач2 на
время завершения осадконакопления
комплекса Ач1, контуров северного и
южного
ПКВ,
положительных
и
отрицательных аномалий палеоглубин
(по результатам тред-анализа III-го
порядка)
3) Комплексирование палеоструктурной
поверхности кровли комплекса Ач1 на
время завершения осадконакопления
комплекса БВ10, контуров северного и
южного
ПКВ,
положительных
и
отрицательных аномалий палеоглубин
(по результатам тред-анализа III-го
порядка)
28

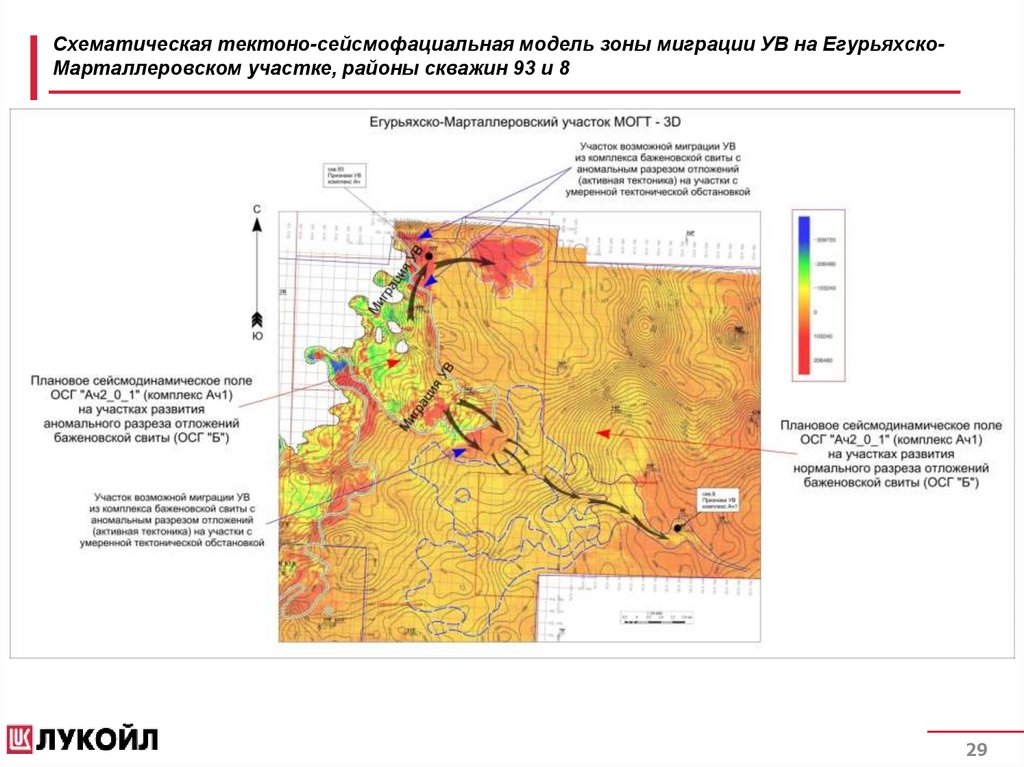
29.

Схематическая тектоно-сейсмофациальная модель зоны миграции УВ на ЕгурьяхскоМарталлеровском участке, районы скважин 93 и 8
29

30.

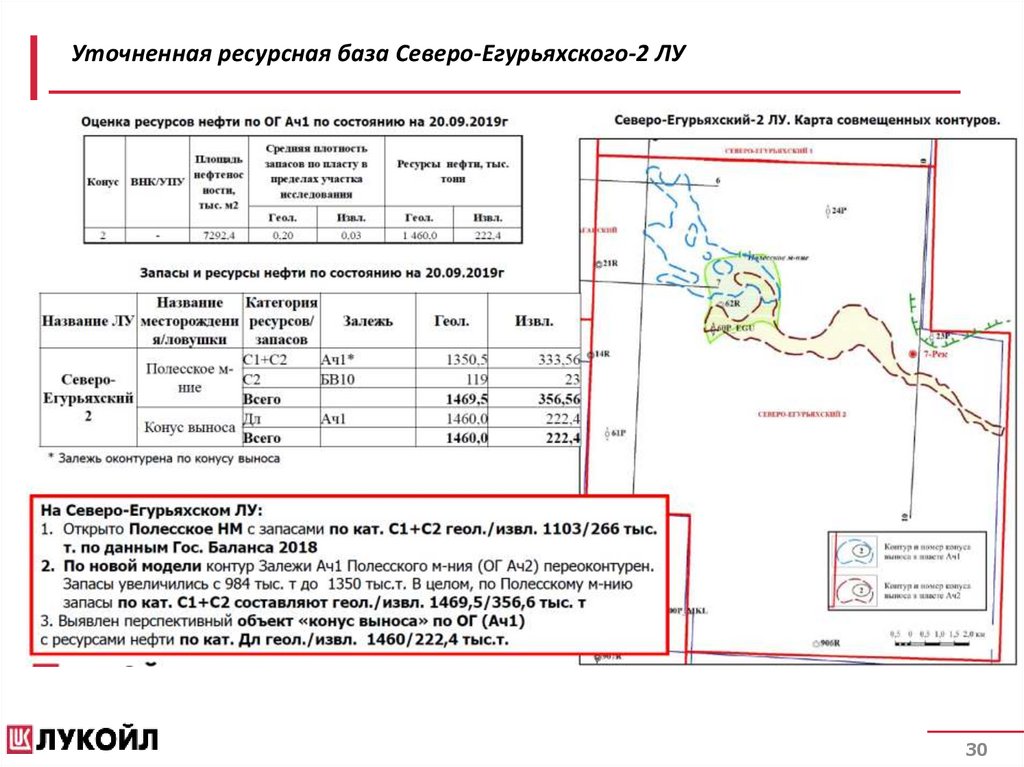
Уточненная ресурсная база Северо-Егурьяхского-2 ЛУ
30

31.

СПАСИБО ЗА ВНИМАНИЕ
Всегда в движении!

32.

Егурьяхско-Марталлеровская площадь МОГТ-3D,
Применение тренд-анализа для выявления приуроченности палеоконусов к участкам
различного палеорельефа комплексов Ач1 и Ач2
Поверхность тренда I-го
порядка для
палеокровли комплекса
Ач2 на время
завершения
осадконакопления в
палеобассейне
комплекса БВ10
Сопоставление поверхностей тренда
разного порядка
в плане и в виде 3D-поверхностей.
Полиноминальные регрессии:
А – линейная,
Б – квадратическая, В – кубическая.
Поверхность тренда III-го порядка
для палеокровли комплекса Ач2 на
время завершения
осадконакопления в палеобассейне
комплекса Ач1
Поверхность тренда III-го порядка для палеокровли комплекса Ач1
на время завершения осадконакопления в палеобассейне
комплекса БВ10
15

33.

16

34.

17

35.

18